基于GeoClaw海啸数值模拟程序对2011年日本东北大地震有限断层模型的验证

胡 培, 景惠敏*, 杨 炜

基于GeoClaw海啸数值模拟程序对2011年日本东北大地震有限断层模型的验证

胡 培1, 景惠敏1*, 杨 炜2

（1.宁波大学 机械工程与力学学院, 浙江 宁波 315211; 2.宁波大学科学技术学院, 浙江 宁波 315300）

由于海啸波具有长周期、慢衰减的特征, 对于能够激发海啸的海底地震, 海啸波资料一定程度上可以作为利用地震波资料和大地测量资料反演得到的震源有限断层模型的补充数据, 以验证该模型的合理性. 本文以2011年日本东北大地震海啸期间反演的震源模型为例, 利用Okada弹性半无限空间理论将震源有限断层模型转化为垂向海底变形; 然后利用GeoClaw海啸数值模型进行海啸数值模拟, 在计算区域模拟实际观测点的海啸波波形数据; 并将模拟海啸波波形数据与实际观测值进行对比, 以验证震源有限断层模型的可靠性.

日本东北大地震; 有限断层模型; GeoClaw数值模拟

2011年3月11日(UTC), 在日本东北部发生了M9.0级地震[1], 引发了海啸灾难, 造成大量房屋冲毁, 近2万人失踪与死亡. 该地震是日本记录以来震级最大的一次地震[2]. 对于此次发震机制和破裂特征, 国际各地震研究所利用观测网记录的各种观测数据进行研究, 根据不同的数据得到了各自的有限断层模型[3-7], 结果显示各断层模型差异明显. 目前, 震源机制测定可根据地震波资料和大地测量资料反演来实现[8]. 但对于特大地震而言, 这两种资料反演的工作都存在不同程度上的欠缺[9]. 对于激发海啸的特大地震, 其海啸波具有长周期、慢衰减的特点, 从而可在一定程度上佐证各有限断层模型的合理性. 一般来说, 我们可以借助成熟的海啸数值模拟程序计算出海底变形引起的海啸波[10], 将模拟波形与各观测站观测数据进行对比, 进而来论述各有限断层模型的合理性[11].

在海啸数值模拟方面, 国际上主要采用MOST[12]、TUNAMI-N1[13]、COMCOT[14]等数值模型进行海啸数值模拟, 此类数值模拟均采用有限差分法求解二维浅水方程. 有限差分法通过泰勒展开式来构造微分方程中各阶导数, 利用差分替代微商, 其离散得到的代数方程没有实际的物理意义, 仅在数值上接近. 另外, 在进行网格计算时, 会产生数值频散现象影响海啸模拟结果.

近年来, GeoClaw模型[15]开始广泛应用于海啸的数值模拟, 该模型使用有限体积法求解非线性浅水方程. 有限体积法对控制方程进行积分, 然后采用高斯定理将扩散项和对流项的体积积分转化为面积分, 得到的方程能够表示控制容积内物理量的守恒. 这种守恒的特性在处理有间断问题时(如海啸)依旧具有合理性. 同时, 该模型使用自适应网格细化技术, 通过预先设定的阈值, 确定需要进行细化的计算区域, 将细化的网格嵌套在粗网格上, 网格层层嵌套, 对空间与时间的步长进行细化. 相比于其他数值模型的网格处理, 具有较高的计算效率, 同时还具有较为满意的精度. 因此, 本文采用该模型进行海啸数值模拟.

本文使用GeoClaw和30′精度海底地形数据对各有限断层模型进行数值模拟, 期望通过使用合理的数值模型以及高分辨率的海底地形数据提供贴近实际的模拟条件, 使得各有限断层模型的合理性论述结果更具有说服力.

1 海啸数值模拟的构建

总体上讲, 海啸的数值模拟需要经过三个阶段: 海啸激发阶段, 海啸传播阶段和上岸阶段. 海啸激发阶段即海底地震发生时, 引发海底断层发生大规模变形, 使得海底表面产生一个突发的变形, 使海平面发生抬升. 与海啸的越洋传播相比, 震源断层的变形在极短时间内完成, 因此在海啸数值模拟中, 通常将海底变形与海平面水位的抬升作同步处理. 海面抬升水位在重力作用下向四周扩散, 并发展成重力长波. 由于海啸传播的大尺度特征, 模拟海啸传播过程中应考虑地球曲率等因素. 上岸阶段即海啸传播至海岸浅水地段, 海啸波波长急剧短缩, 海啸波波高急剧增加, 形成巨大的“水墙”. 此阶段由于水动力过程的非线性增强, 需要配合高分辨率地形数据进行计算以提升数值模拟的准确性, 而由于高分辨率地形数据的缺乏, 海啸数值模拟的准确度受到了较大的限制. 本文使用30′精度的SRTM30地形数据(Shuttle Radar Topography Mission, http://www2.jpl.nasa.gov/srtm/)进行海啸数值模拟, 期望得到一个较为合理的模拟结果.

1.1 海啸源

2011年3月11日日本东北地震发生之后, 国际地震研究机构根据初步震源机制、断层模型等参数确定了各自的震源有限模型[10]. 其中, 包括美国国家地质调查局提供的平均位错模型、USGS瞬时破裂模型和USGS分时破裂模型, 中国地震局地球物理研究所提供的IGPCEA模型, 中国科学院地质与地球物理研究所提供的IGCAS模型以及日本国土地理院提供的GSI模型. 其具体参数见表1.

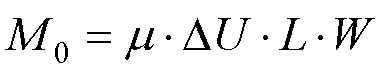
表1 各地区地震研究机构有限断层模型的参数

图1 IGCAS模型断层分布图

图2 IGCAS模型海底变形图

1.2 传播模型

GeoClaw模型是Conservation Laws Package (ClawPack)软件用于模拟地震海啸的模块. 其实现的技术路径可分为两步: 第一步, 利用Okada弹性半无限空间理论将有限断层模型转化为海底垂向变形, 进一步转化为海面的初始水位; 第二步, 使用有限体积法求解二维浅水方程, 并考虑海底底部摩擦对于海啸波传播的影响, 同时引入了非线性限制器来抑制数值计算过程中产生的非物理振荡, 使其在空间和时间都达到了二阶精度, 并且采用自适应网格技术, 对海啸波进行追踪, 并在波高变化剧烈的区域进行网格加密, 来达到减少计算量及提高计算效率的目的.

模型的控制方程的守恒形式如下:

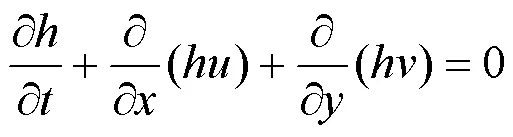
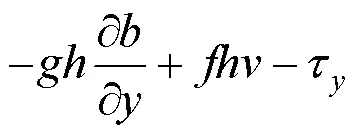
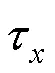
式中:为曼宁系数, 取0.025.

1.3 模型设置

本文海啸波传播模型计算区域为60°E～60°W, 80°S～80°N. 将计算区域划分为以1°为间隔的粗网格, 共生成38400个网格. 并设置二级、三级精细化网格, 精度分别为30′和5′. 采用自适应网格技术, 一般模拟时使用1°精度网格; 当模拟的过程值达到阈值时, 切换至高分辨率网格, 继续网格推进, 以达到优化计算效率的目的. 同时, 采用精度为30′的STRM30地形数据, 以提高模拟海啸上岸阶段的准确率.

模拟所用的海啸观测数据由NOAA(National Oceanic and Atmospheric Administration, https:// ngdc.noaa.gov/hazard/dart/2011honshu_dart.html)提供, 图3为NOAA提供的2011年日本东北大地震海啸传播时间图. 图中表示了海啸在不同时刻所在的位置, 图中标有数字的方块为该区域中记录到海啸波的浮标, 用于记录浮标点处不同时刻的水位高度, 同时NOAA给出了各观测点处的拟合潮汐分量与残差值. 其中, 拟合潮汐分量为仅在潮汐影响下不同时刻的水位高度; 残差值为观测数据与拟合潮汐分量之差, 即除潮汐影响之外不同时刻的水位高度变化.

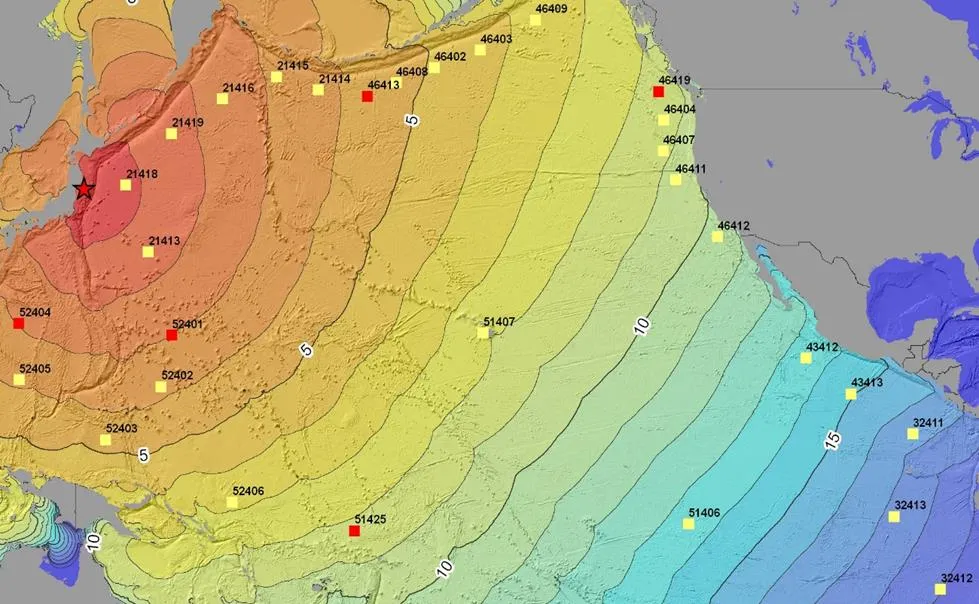
图3 2011年日本东北大地震海啸传播时间图

本文将使用残差值与模拟海啸波对比来论述模拟海啸的合理性. 为保证模拟海啸结果的合理性, 应使用多点浮标数据与模拟海啸进行比对, 同时对各浮标残差值进行分析筛选, 筛选原理为观察海啸波到达该浮标点之前是否存在异常值. 以46402点、46407点为例, 图4为46402点与46407点的残差时序图, 46402点在海啸波到达之前, 残差在-0.05m附近波动, 当海啸波到达该潮汐站时, 残差为0.08538m. 此时可以认为当海啸波传到该浮标点时存在其他因素对海面高程产生影响, 此点与模拟海啸数据差异较大的可能性应是其他因素导致实际观测数据异常, 而不是模拟结果有问题. 46407点在海啸波到达之前, 残差数值在零附近波动, 当海啸波到达该浮标, 残差值产生明显变化. 则可以认为在海啸波传至该点前并无其他因素对其附近海面产生影响, 所记录残差即由海啸波产生. 此类浮标数据可与模拟数据进行对比.

使用上述筛选准则对上述浮标进行筛选, 并最终确定18个浮标, 同时在计算区域内设置对应的监测点. 浮标位置信息详见表2.

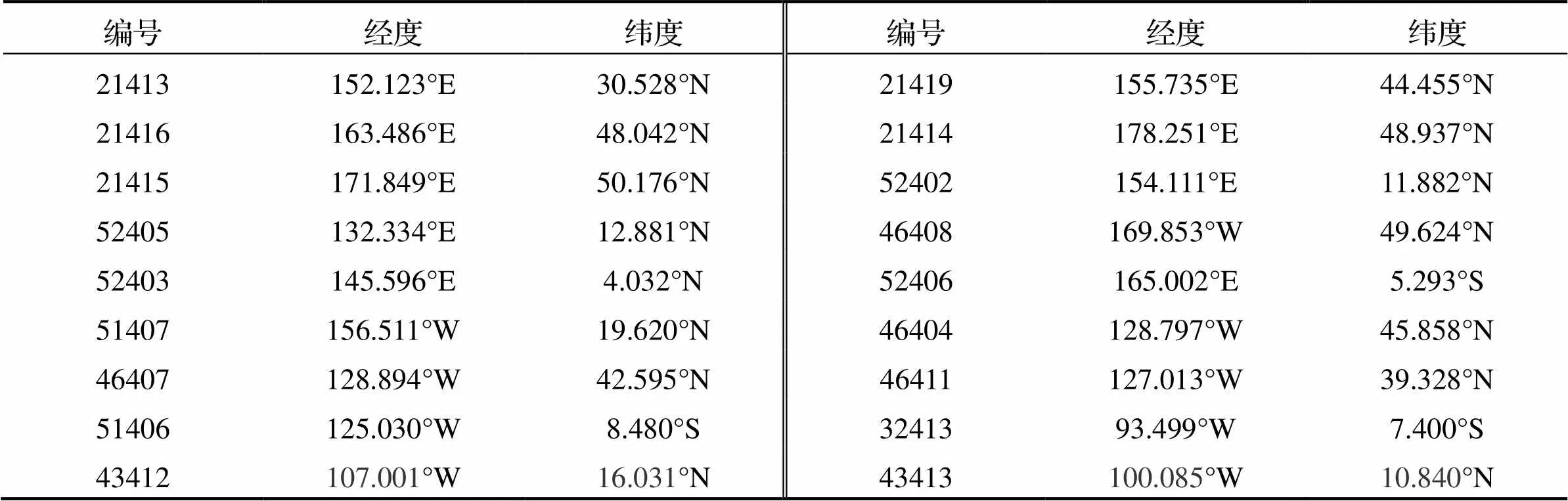
表2 所选中的浮标列表

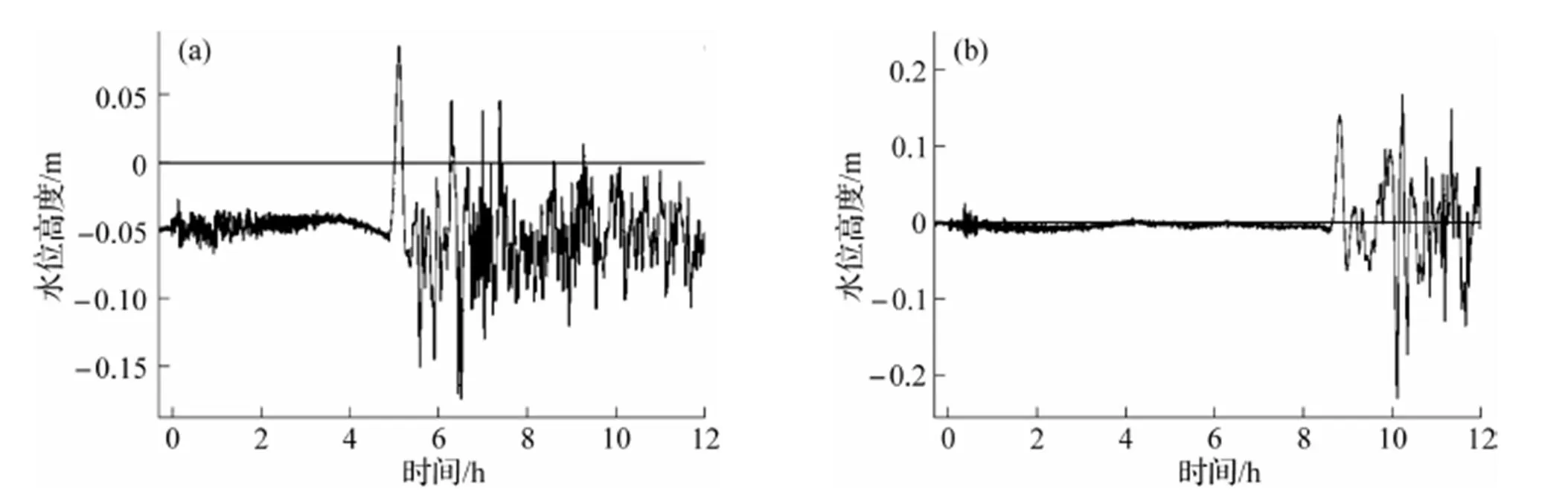
图4 46402点(a)与46407点(b)的残差时序图

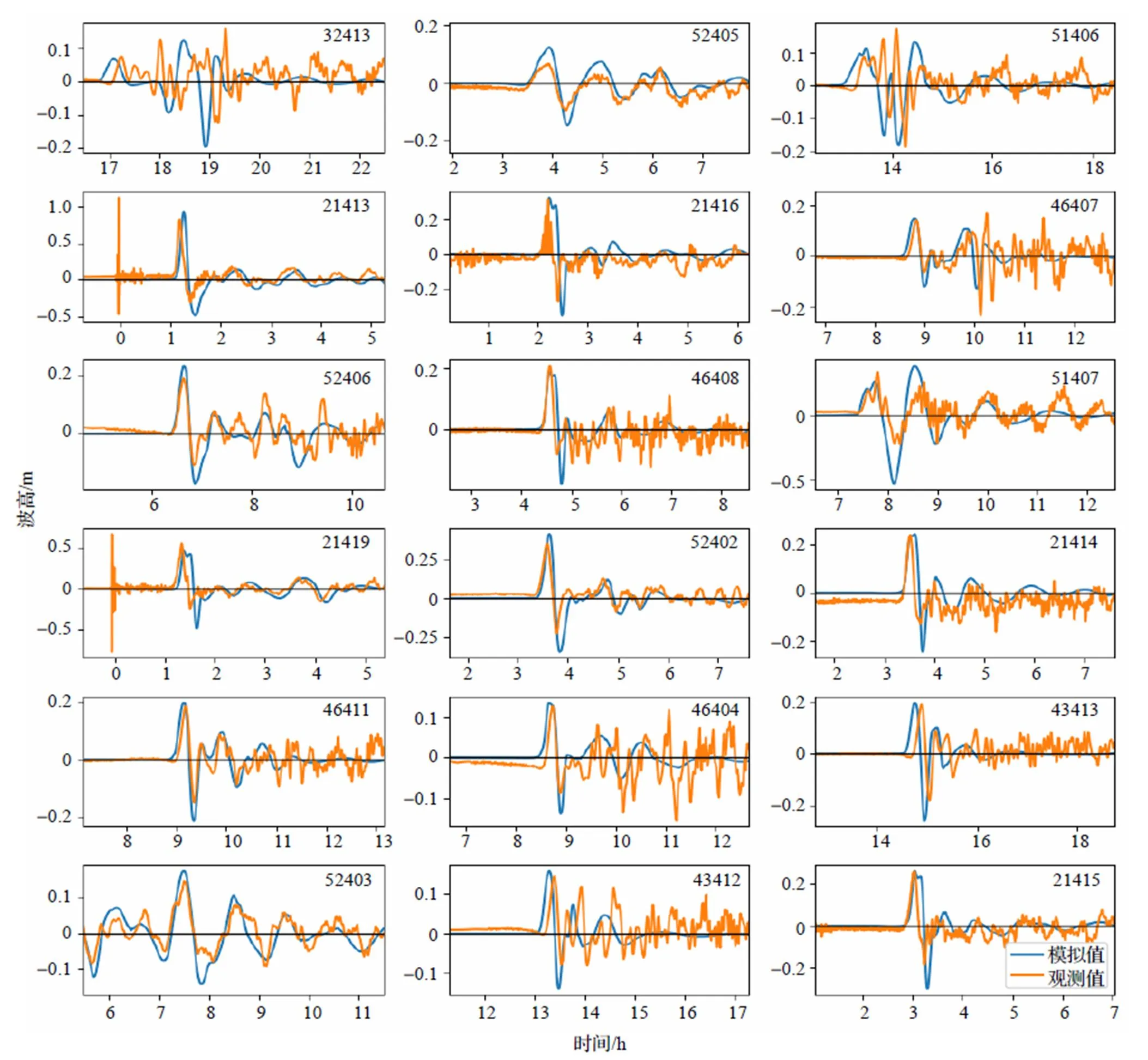
图6 各观测点记录的海啸波传播时程曲线

2 海啸数值模拟

2.1 IGCAS模型海啸数值模拟

本文共使用6种地震有限断层模型来进行海啸数值模拟, 本节以IGCAS模型进行阐述.

IGCAS断层模型在海底破裂引发了海平面的抬升, 抬升水位受到重力影响向四周扩散形成海啸波. 同时当模拟海啸传播时, 设置在浮标坐标处的监测点记录海面水位的变化. 图5、图6分别为IGCAS模型激发的海啸在2h内的传播过程以及各监测点所记录的海面水位时序变化情况.

图6中, 颜色较浅曲线表示各浮标点记录的残差值随时间的变化, 颜色较深曲线则为模拟海啸传播时各监测点所记录的海面随时间的变化, 横坐标以海啸激发的时刻为0, 纵坐标以海平面为基准海面水位. 通过观察各个浮标点观测值与模拟值的对比并对其进行分析: (1)21413点与21419点的观测值在0时附近出现异常值. 两点距离震源有一定距离, 而异常值出现在海啸激发时, 因此可基本排除是由海啸波传播引起的海平面变化; (2)各监测点所记录的模拟海啸波的波形基本上都与浮标点所记录的残差数据吻合. 同时对于接近震源的监测点(21413点、21414点、21415点等)模拟海啸波的到时晚于实际海啸波, 而对于距离震源较远监测点, 模拟海啸波的到时早于实际海啸波. 此现象在32413点与51406点表现最为明显. 因此可以认为使用IGCAS模型在进行模拟海啸时, 海啸波波速略大于实际海啸波的波速. (3)使用IGCAS模型进行海啸数值模拟时, 模拟海啸可以较好地匹配实际海啸的波高与到时. 但是当海啸波穿过该浮标点之后, 实际观测数据中依旧存在较大幅度的海面波动, 而模拟海啸的海啸波在穿过监测点之后, 海面迅速趋于水平状态. 造成这种情况的原因主要是由于在设置边界条件时, 采用了开放式边界, 因此无法考虑海啸波传播至固体界面时产生的反射波对海面的影响.

表3 各监测点模拟波高与实测波高差值

注: (1)绝对差(m)=观测波高-模拟海啸波高; (2)相对差(%)=(观测波高-模拟海啸波高)/实测残差.

2.2 各有限断层模型误差分析

分别将各个震源模型模拟得到的监测点海面波动时序图与对应浮标数据进行对比, 均可在浮标数据时序图中匹配到相应形状. 模拟结果和实测数据的接近程度可以在一定程度上反映模拟程序的可靠性, 形状的匹配程度一般由海啸传播至观测点时的波高与到时所控制, 而通过观察各观测点的模拟结果与浮标数据的对比, 并没有发现模拟海啸波到时严重偏离实际海啸波到时的现象. 因此, 研究各断层模型海啸模拟结果可靠性的问题便简化成了通过对比各观测点模拟海啸波高的误差来分析各断层海啸模拟结果的可靠性问题. 表3即为各监测点上观测波高与模拟波高之间的绝对差以及它们的相对误差.

图7 各观测点模拟波高与实测波高绝对差

图8 各观测点模拟波高与实测波高相对差

为更直观地了解数据变化趋势, 将上述观测点根据海啸波到时进行排序并在图中表示, 图7为各观测点模拟波高与实测波高绝对差图, 图8为各观测点模拟波高与实测波相对差图

通过对上述的数据与图形进行分析评价各有限断层的合理性, 最终得出如下结果:

(1)从图7可以发现, 各观测点的绝对误差总体还是随着传播时间的增加变小. 当海啸波向四周海域传播时, 海啸的能量也开始进行消耗, 最直观的表现即海啸波波高的降低. 若观测点处无其他干扰因素, 一般情况下传播时间长的观测点模拟波高与观测波高的差值普遍较小. 由于较远观测点残差较低, 在进行相对误差分析时, 若存在其他因素干扰, 则极易在相对误差中放大. 因此, 就出现了图8的情况, 即在绝对误差较小的点处, 却有着较大的相对误差.

(2)平均位错模型与GSI模型相较于其他模型, 在准确性上存在较大差距. 通过简单分析可知, 平均位错模型得到的震级虽然与现实接近, 但是该模型只存在一个断层, 由断层破裂引起的海底变形相对平均, 即地震能量并不集中, 因此模拟得到的海啸波波高普遍低于实际观测值. 对于GSI模型而言, 本身计算得到的地震矩小于实际情况, 因此不难发现该模型的模拟波高均小于观测波高. 虽然, 两个模型的准确性有待提升, 但是不可否认这两个模型在海啸波的到时以及各监测点的海平面变化趋势与实际观测的海平面变化具有一定的吻合. 而使用这些模型(尤其是平均位错模型)进行海啸预警时, 在预测海啸波传播位置的确定性方面具有一定的参考价值.

(3)IGCAS模型的模拟结果与实际观测数据较为接近, 其18个监测点中仅存在2个点数值异常. 在32413点, 所有断层模型均具有较大的误差, 并且该点距离震源距离是所有18个点中最远的, 本身距离越远, 模拟结果的准确率就容易下降, 但同时也不能排除其他干扰因素导致该点海面变化异常的可能性. 在51407点, 实际波高与IGCAS模型的模拟波高差为12.2cm, 相对误差为46.47%. 而IGPCEA模型、USGS瞬时/分时模型在该点的相对误差分别为26.07%、－4.38%、－9.12%. 这3个模型在该点模拟结果表现良好, 可排除其他因素对该浮标点检测数据造成影响. 因此, 可认为IGCAS模型在51407点处的模拟结果确实存在较大误差. 所以, 当使用该模型进行海啸数值模拟时, 应警惕可能出现的异常观测点.

(4)通过USGS瞬时破裂模型与分时破裂模型的模拟结果的对比, 我们可以初步得到以下结论: 对于范围大、持续时间久的海啸传播过程, 分别使用相同断层参数的瞬时破裂模型与分时破裂模型进行海啸数值模拟, 模拟的海啸波在远场海域基本无影响, 在距离震源较近的观测点(21413点)处虽存在一定差异, 而相较于本身的波高来说, 差异也在可接受范围内. 此结论在本次日本东北地震海啸模拟中成立, 但在更大范围内的适用性还需要后续更多验证.

(5)IGPCEA模型的模拟结果与实际数据接近. 虽然在18个监测点中, 51406点与32413点模拟数据与实际观测数据对比有一定差距, 考虑到这两个观测点与震源的距离较远, 结合其他模型均在该点处有较大相对误差, 因此我们可以初步认为在这两点出现了其他的因素影响海面水位的变化. 因此, 初步可以认为使用IGPCEA模型进行的海啸数值模拟时, 其模拟结果具备较好的准确性.

3 总结

本文对现有日本东北大地震断层模型进行海啸数值模拟, 以进一步论述各断层模型的合理性. 此方法的讨论虽早已存在, 但因为受到当时海啸数值模型以及地形数据精度等限制, 模拟得到的结果不尽人意. 现今, 笔者使用GeoClaw海啸数值模型与更高精度的地形数据进行海啸数值模拟, 期望获得更为精确的结果. 通过各断层模拟结果之间的横向对比, 最终, IGPCEA模型的模拟结果与实际观测结果更为接近, 表明此断层模型相较于其他断层模型较为合理.

本次的研究依旧存在不少需要加强之处. 在海啸的数值模型上, 对数值模型的边界设置仅采用了开放式边界, 而忽略了海啸波传播至固体边界产生的反射波对海面的影响. 另外, 在进行此类越洋海啸的数值模拟时, 忽略了科里奥利力对海啸传播的影响. 在观测数据选择上, 直接使用了残差值作为海啸观测数据, 而忽略了其他因素(如风暴潮、飓风等)对于残差值的影响. 期望在未来的研究中, 通过对海啸数值模型的优化与升级得到更加具有说服力的模拟结果.

[1] JMA. The 2011 off the Pacific coast of Tohoku Earthquake 28th report[R]. 2011.

[2] USGS. Largest earthquakes in the world since 1900[R]. 2011.

[3] Hayes G P. Rapid source characterization of the 2011M9.0 off the Pacific coast of Tohoku Earthquake[J]. Earth, Planets and Space, 2011, 63(7):529-534.

[4] Hayes G P, Earle P S, Benz H M, et al. 88 hours: The U.S. geological survey national earthquake information center response to the 11 March 2011M9.0 Tohoku Earthquake[J]. Seismoligical Research Letters, 2011, 82(4):481-493.

[5] 张勇, 许力生, 陈运泰. 2011年3月11日日本本州东海岸近海地震破裂过程快速反演结果v1[EB/OL]. [2021- 05-16]. 中国地震局地球物理研究所. http://ddsep.cea- igpac.cn/rp/2011/20115e74367081165e565e5672c4e1c6d775cb88fd16d7757309707783488fc77a0b5fe901f53cd6f147ed3679c.

[6] Wang W, Hao J, Yao Z. Preliminary result for rupture process of Mar.11, 2011,M8.9 earthquake, near the East Coast of Honshu, Japan [EB/OL]. [2021-05-22]. http:// www.igg.cas.cn/xwzx/zhxw/201103/t20110312_3082869.html.

[7] Imakiire T, Kobayashi T. Crustal deformation and fault model of the 2011 off the Pacific coast of Tohoku Earthquake[J]. Bulletin of the Geospatial Information Authority of Japan, 2011, 2011:70-79.

[8] 王振, 孟国杰, 横田佑助, 等. 利用1-Hz GPS波形数据反演2011年日本东北大地震震源破裂过程[J]. 地震, 2013, 33(3):13-23.

[9] 周正阳, 张勇. 利用海啸波数据反演特大海啸地震的地震矩张量[C]//2015中国地球科学联合学术年会论文集(十三)——专题37地球气候系统历史、专题38强震机理、孕育环境与地震活动性分析、专题39大数据时代地球物理信息学及其应用. 北京, 2015:2.

[10] 景惠敏, 张怀, 吴忠良, 等. 利用海啸数值模拟结果进行海底地震有限断层模型验证[J]. 地震, 2013, 33(4): 207-213.

[11] 艺帆, 安超. 海啸反演对于断层位置不确定性的敏感性分析[C]//2020年中国地球科学联合学术年会论文集(十五)——专题四十三: 海洋地球物理、专题四十四: 海啸及海啸预警研究、专题四十五: 电磁地球物理学研究应用及其新进展. 重庆, 2020:27.

[12] Titov V V, Gonzalez F I. Implementation and testing of the method of splitting tsunami (MOST) model. [EB/OL]. [2021-05-22].https://www.pmel.noaa.gov/pubs/PDF/tito 1927/tito1927.pdf.

[13] Imamura F, Shuto N, Goto C. Numerical simulations of the transoceanic propagation of tsunamis[C]//Proceedings of the Sixth Congress Asian and Pacific Regional Division, IAHR. Kyoto, Japan. 1988:265-272.

[14] 潘文亮, 王盛安. COMCOT数值模式的介绍和应用[J]. 海洋预报, 2009, 26(3):45-52.

[15] George D L, LeVeque R J. Finite volume methods and adaptive refinement for global tsunami propagation and local inundation[J]. Science of Tsunami Hazards, 2006, 24(5):319.

[16] Okada Y. Surface deformation due to shear and tensile faults in a half-space[J]. Bulletin of the Seismological Society of America, 1985, 75(4):1135-1154.

[17] Hanks T C, Kanamori H. A moment magnitude scale[J]. Journal of Geophysical Research: Solid Earth, 1979, 84 (B5):2348-2350.

（责任编辑 章践立）

Verification of finite fault model of the 2011 Tohoku Tsunami based on GeoClaw tsunami simulation model

HU Pei1, JING Huimin1*, YANG Wei2

( 1.Faculty of Mechanical Engineering & Mechanics, Ningbo University, Ningbo 315211, China;2.College of Science & Technology Ningbo University, Ningbo, 315300, China )

Tsunami waves are characterized by long periods and slow subsidence. For the submarine earthquake triggering a tsunami, the tsunami waveform data can be used as supplementary data for verifying the rationality of the finite fault model obtained by inversion of seismic wave data and geodetic data. Taking the earthquake source of the 2011 Tohoku tsunami as an example, we transform the finite fault model into vertical variation in the seabed topography according to Okada elastic half-space theory. Then we use the GeoClaw tsunami model to perform the tsunami simulation. Some monitoring points in the calculation domain are set on those points which can be utilized to obtain the tsunami waveform data. By comparing the simulated tsunami waveform data with the actual observation data, we analyze the reliability of the models and verify the effectiveness of most reasonable finite fault model of the earthquake.

Tohoku earthquake; finite fault model; GeoClaw numerical simulation

P315

A

1001-5132（2022）03-0106-09

2021−10−08.

宁波大学学报（理工版）网址: http://journallg.nbu.edu.cn/

国家自然科学基金青年科学基金（41304072）.

胡培（1993－）, 男, 浙江宁波人, 在读硕士研究生, 主要研究方向: 海啸数值模拟. E-mail: hup93@outlook.com

通信作者:景惠敏（1984－）, 女, 山东德州人, 博士, 主要研究方向: 地震海啸的数值模拟. E-mail: jinghuimin@nbu.edu.cn