弯管对超声波流量计测量精度的影响及改善措施
刘亚男, 杨 鸣
弯管对超声波流量计测量精度的影响及改善措施
刘亚男, 杨 鸣*
(宁波大学信息科学与工程学院, 浙江 宁波 315211)
流体经过弯管易产生二次流、涡流等扰流情况, 使流道内流速分布不均匀, 会对流量计的测量精度产生影响. 为研究扰流对流量计的影响, 利用建模与模拟仿真方式, 对G16型号单流道流量计在入口管道为双弯管及半月双弯管情况下的计量效果展开研究, 计算两种情况下相对于入口管道为直管时的流量误差度, 以此表明单流道流量计在安装弯管时, 扰流给测量结果带来的误差. 为减小此类误差, 建立G16型号双流道流量计模型, 并对其进行完全相同条件下的仿真实验, 最后将所得数据与单流道流量计对应数据进行对比分析. 结果表明, 双流道流量计相对于单流道流量计在各流量下的测量精度均有所提高. 当流量为2.5m3·h-1及10m3·h-1, 入口管道为半月双弯管时, 测量精度分别提高了1.0940%和1.2058%; 入口管道为双弯管时, 测量精度分别提高了2.1120%和2.2930%. 双流道流量计相比于单流道流量计, 较大程度地改善了弯管带来的扰流影响, 且计量精度有效提高.
超声波流量计; 弯管; 单流道; 双流道; 模拟仿真
气体超声波流量计具有计量精度高、量程比大、性能稳定、管道中无压力损失等特点, 相比传统流量计优势显著, 其在天然气流量计量领域得到了广泛应用, 且发展迅速[1]. 如何提高超声波流量计的测量精度是当前此领域研发的要点. 作为速度式流量仪表, 其测量精度受流道影响较大, 因此理想情况是流道呈充分发展状态[2]. 但在实际安装过程中, 由于受前置弯管、开关阀门等器件影响, 流道很难达到这种状态[3]. 研究表明, 在流量计入口处安装足够长的直管可以有效改善这种情况[4], 但实际安装时由于空间限制, 无法满足前置长直管的要求, 因此通常需要前置弯管, 而前置弯管会导致二次流和涡流等扰流, 使流道内流速分布不均匀[5]. 当前, 国内一些超声波流量计厂商所使用的G16型号单流道具有以下缺点: 探头发出的超声波可覆盖范围小, 靠近流道前后壁面有较大部分流速无法测得. 因此使用该流道的流量计, 且当其入口管道为弯管时, 测量结果就会不准确.
本文首先对使用单流道的流量计测量精度进行研究, 流量计入口管道分别安装直管、双弯管和半月双弯管, 将安装这3种管道的流量计分别导入FloEFD仿真软件进行仿真, 结果表明安装双弯管和半月双弯管的流量计产生的相对误差较大, 说明弯管给其测量精度带来较大影响. 然后基于此G16型号单流道在结构上存在的缺点, 对其进行改善并增加流道数, 构建G16型号双流道超声波流量计, 并通过与单流道流量计同等条件下的仿真实验, 证明双流道超声波流量计的抗扰流能力优于单流道超声波流量计. 研究结果能为提高弯管安装下流量计的测量精度提供相关参考.
1 超声波流量计的原理
超声波流量计的流速测量以时差法为主, 以发射和接收换能器之间的连线作为超声波的传播路径[6]. 直射式和反射式为单声道最常见的两种布置方式. 采用直射式布置方式时, 抗漩涡流和交叉流的能力较弱, 而反射式声道布置能有效克服复杂流场带来的不利影响, 同时声道长度的增加使渡越时间的测量更加准确, 因此在小管道流量测量中采用这种布置方式能发挥较大优势[7]. 本文中的流道均使用的反射式声道布置方式, 其测量原理如图1所示.

图1 时差法反射式声道测量原理

图2 直管正视图

图3 双弯管正视图

图4 半月双弯管纵向剖面图

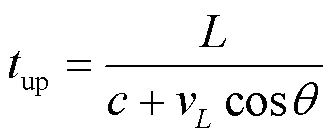



2 入口管道模型设置
在实际使用中, 流量计会在进气管道前配有开关阀门, 管道内部安装有一块隔板, 进气管道为双弯管, 且隔板为半开状态时, 扰流影响最大. 在此安装条件下, 若仿真效果依然理想, 则代表流量计的计量性能好. 因此, 本文除直管与双弯管外, 还增加半月双弯管. 管道公称直径=46.5mm, 直管长度为5. 双弯管中弯管半径=1.5, 入口缓冲区管道长度为5, 出口缓冲区管道长度为3. 半月双弯管即在2个弯头间增加半管面积板, 开口朝向第一个弯管的外部半径. 管道模型图如图2~图4所示.
3 入口管道安装效应仿真
图5~图7分别为上述3种入口管道下的横向速度等高线及矢量切面图. 入口体积流量均为25 m3·h-1, 测量段均设置在下游直管道最底部. 由直管安装效应仿真图看出, 管道外周速度较低, 流体集中流向管道中部, 流速分布均匀, 整体效果较为理想. 从双弯管安装效应仿真图可以看到二次流速度呈对称涡旋分布情况, 说明气流经过双弯管后不仅只有沿管道的轴向速度, 还产生了径向分速度[8-9]. 从半月双弯管安装效应仿真图中看出靠近双弯管上游直管轴向一侧的速度较低, 另一侧速度较高, 且同样有二次流速度涡旋分布情况. 由此说明, 气流经过弯管会形成扰流, 到达流道内时, 使流场分布受到影响, 从而给测量结果带来误差.
4 G16单流道超声波流量计仿真研究
4.1 模型建立
利用Creo建模软件构建如图8所示G16型号单流道超声波流量计模型, 其中主要器件有流道、入口阀门以及与流道连接的出气通道. 流道模型如图9所示. 矩形流道长132mm, 在流道内部加装23个整流片, 隔片厚度为0.3mm, 长度为51.2mm, 流道内部宽45.3mm, 高22mm. 一对超声波换能器安装在流道上侧, 形成反射型单声道测量模式. 相邻整流片之间的距离为1.6mm. 下面将通过仿真对此流量计的计量效果展开研究.

图5 直管安装效应仿真图

图6 双弯管安装效应仿真图

图7 半月双弯管安装效应仿真图

图8 G16单流道流量计模型

图9 G16单流道模型
4.2 模拟仿真
计算流体力学(简称CFD)是数值数学和计算机科学结合的产物, 以实现对流体力学的模拟仿真与分析, 能够直观有效地反映出流体流动的状态[10]. 对上述G16单流道超声波流量计分别安装直管、双弯管和半月双弯管入口管道, 弯管安装方向均向左, 出口均安装直管. 将这3个流量计模型分别导入FloEFD仿真软件进行仿真. 体积流量范围为0.16~25m3·h-1. 选取5个流量进行仿真, 分别为min、0.1max、0.4max、0.7max、max.
以入口体积流量为25m3·h-1时的仿真情况为例, 得到图10~12所示的3个流量计的流道中部位置等高线横向切面图. 由图可见, 入口管道为直管情况下, 流道内的流速分布最为均匀, 测量结果最为准确, 因此选择直管情况下得到的数据作为标准值. 当入口管道为双弯管以及半月双弯管时, 流场分布不均匀, 且流速有所降低. 这也再次证明, 弯管引起的扰流进入流道内, 流场分布受到影响.

图10 直管安装流道切面图

图11 双弯管安装流道切面图

图12 半月双弯管安装流道切面图
由于靠近整流片位置有黏性的阻滞作用, 导致此处流速较低, 使其不具代表性, 因此测速线段需位于流道中心处. 由于线段上侧端点必须位于超声波换能器底面上, 因此最多可画出4条连接线模拟传播路径以供计算. 模拟声道连线方式如图13所示(鉴于4条连接线呈平行关系, 因此主视图中只可看见1条连接线). 由于4条测速线所能覆盖的范围小, 靠近流道前后壁面有较大部分流速无法测得, 会对流量计的测量精度造成影响, 这为后文双流道超声波流量计的设计提供了思路.

图13 流道模拟声道连线方式
以流量为25m3·h-1, 入口管道为直管情况下的仿真结果为例, 得到的4条测速线段的线速度与距离间的变化曲线(图14).

图14 25 m3·h-1直管情况下的线速度分布


由于流道中流速分布不均匀, 因此需要将4条路径的平均线速度再求平均值作为最终结果. 计算公式如下:

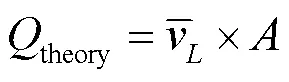
式中:为流道的横截面面积.
根据式(4)、(5)、(6)最终求得入口管道为直管, 流量为25m3·h-1时的理论流量为25.5469m3·h-1. 根据仿真结果求取每个流量下的理论流量, 整理数据结果见表1.
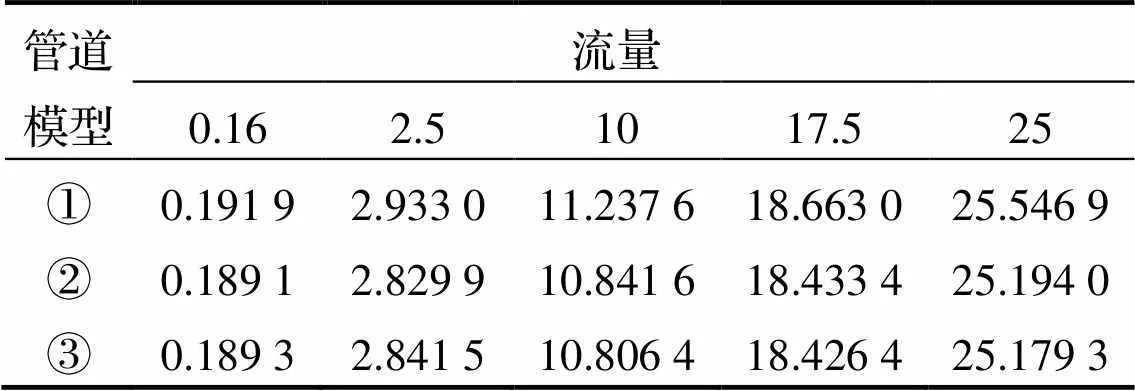
表1 3个流量计各流量对应理论流量值 m3·h-1
注: ①直管; ②双弯管; ③半月双弯管.
4.3 流量误差曲线线性化修正

由此, 流量修正系数K:

根据仿真结果计算得到每个流量对应的修正系数(K保留6位有效数字), 结果见表2.
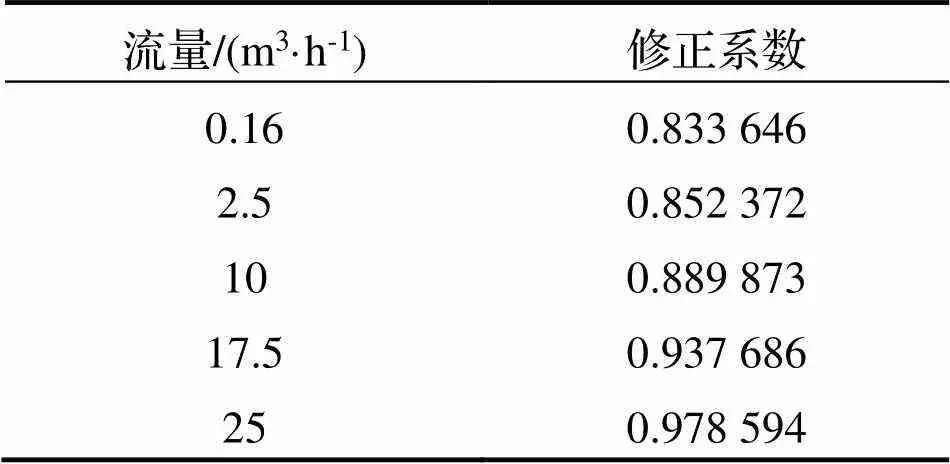
表2 各流量对应的修正系数
误差曲线线性化修正函数采用分段二次曲线拟合, 流量拟合点分别为min、0.1max、0.4max、0.7max、max. 其中min、0.1max、0.4max为第一段拟合; 0.4max、0.7max、max为第二段拟合. 误差修正方程如下:



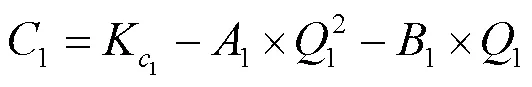
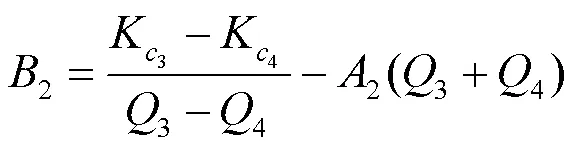
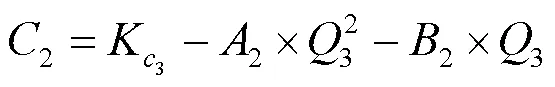
将相应数据代入, 求得修正方程为:



根据分段修正方程可以求得min至max之间任意流量对应的修正系数. 则修正流量公式为:
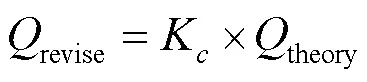
由于本文以直管情况下修正得到的流量值作为标准值, 因此也将其在5个流量下求得的修正系数作为双弯管和半月双弯管入口管道流量计对应流量的修正系数. 则由仿真结果根据式(18)可以得到每个流量计各流量修正后的流量, 再计算误差度. 误差计算公式为:
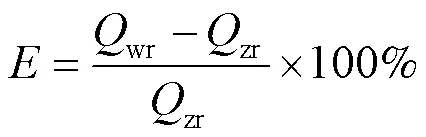
式中:wr为弯修流量;zr为直修流量.
直管误差计算公式为:

表3即为根据式(19)和式(20)得到的3个流量计对应流量的相对误差.

表3 3个流量计对应流量的相对误差


图15 不同管道下单流道流量计相对误差折线图
5 G16双流道超声波流量计模型设计及仿真研究
5.1 数学建模
基于上述G16单流道在结构上存在的缺点, 设计G16双流道. 流量计除流道结构与出气通道有所改变, 其余器件均相同, 矩形流道长107mm, 流道内部宽21.7mm, 高25mm. 声道形式依然是反射型单声道. 流道内部加装9个整流片, 隔片厚度为0.3mm, 长度为58.6mm, 隔片间距离为1.9mm. 流量计以及流道模型结构如图16~图17所示.
5.2 模拟仿真


图16 G16双流道流量计模型图

图17 G16双流道模型图
以入口体积流量为25m3·h-1时的仿真情况为例, 得到如图18~图20所示的3个流量计流道中部位置等高线横向切面图. 与图11~图13相比, 这3个切面图区分度不是很明显, 流场分布较均匀, 但仍可看出, 入口管道为直管时, 流速分布最均匀, 入口管道为双弯管和半月双弯管时, 流场较直管情况下不均匀, 且流速有所减慢. 初步可以断定, 弯管对双流道流量计测量精度的影响小于对单流道流量计测量精度的影响.
双流道内共有8条线段用以模拟传播路径, 与G16单流道相比, 增加了1倍, 且靠近流道前后壁面两侧未能被超声波覆盖的范围减小. 由此推测, G16双流道流量计的测量误差小于G16单流道流量计的测量误差. 模拟声道连线图如图21所示.
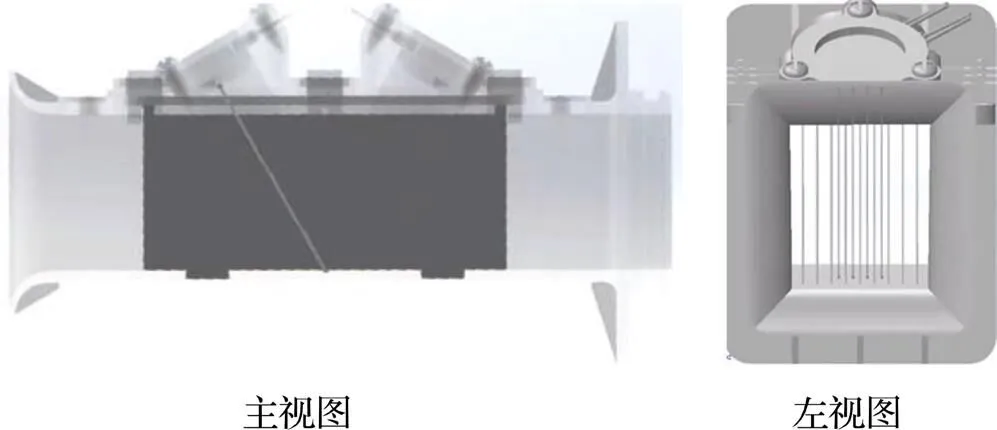
图21 流道模拟声道连线方式图
流道线平均流速计算公式为:

根据仿真结果以及式(6)求取每个流量计对应流量下的理论流量, 最终整理结果见表4.

表4 3个流量计各流量对应理论流量值 m3·h-1
注: ①直管; ②双弯管; ③半月双弯管.
5.3 流量误差曲线线性化修正
表5即为根据仿真结果及式(8)计算得到每个流量对应的修正系数.
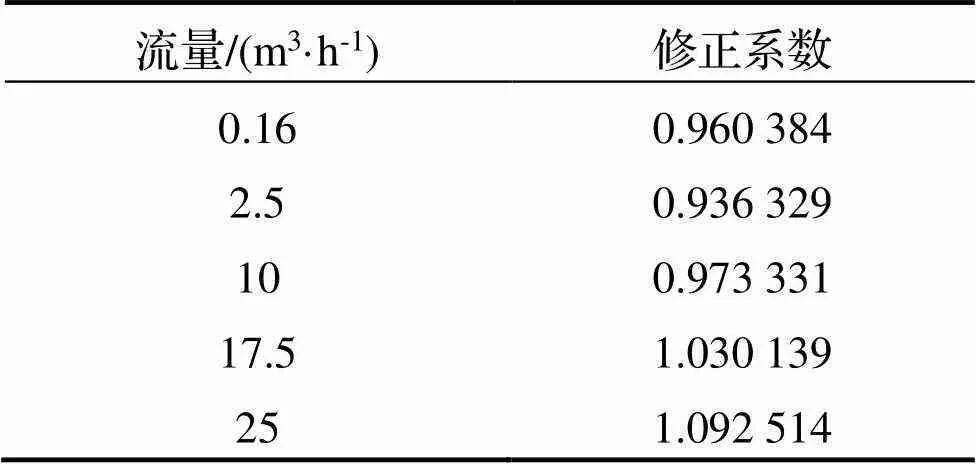
表5 各流量对应修正系数

图18 直管安装流道切面图

图19 双弯管安装流道切面图

图20 半月双弯管安装流道切面图
由式(9)~(15)求得修正方程为:
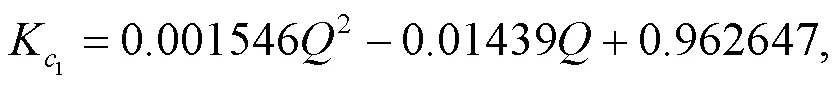
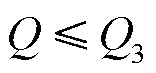

最后, 表6即为由式(19)和式(20)求得的3个流量计对应流量相对误差.

表6 3个流量计对应流量相对误差度
根据表6得到相对误差折线. 如图22可知, 入口管道为直管的流量计, 各流量相对误差均接近于0, 且全部满足国家标准; 入口管道为双弯管的流量计, 各流量相对误差全部满足国家标准; 入口管道为半月双弯管的流量计, 在为2.5m3·h-1以及10m3·h-1时, 相对误差不满足国家标准. 图22与图15相比可知, 弯管给双流道流量计带来的误差小于文中的单流道流量计, 流道有所改进, 但仍可进一步改善.
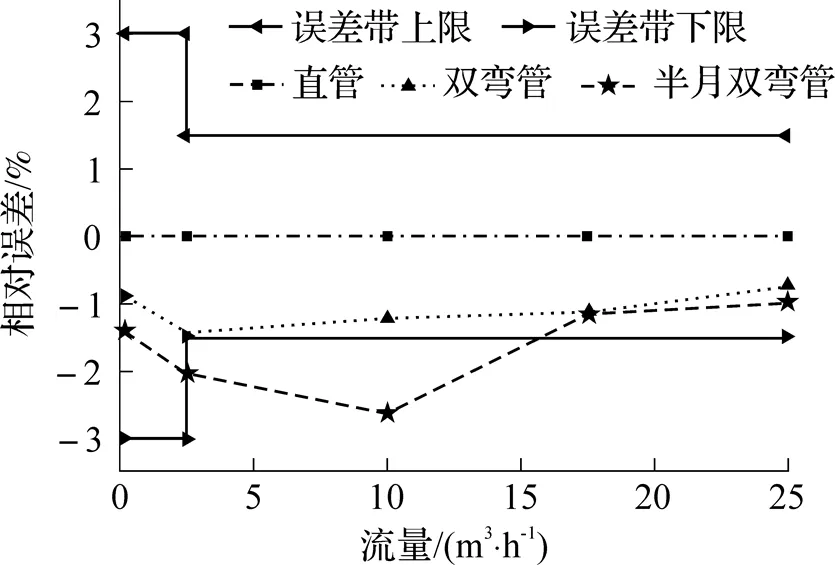
图22 不同管道下双流道流量计相对误差折线图
6 双流道与单流道流量计的计量精度比较
根据表3与表6中的数据, 计算入口管道分别安装2种弯管时, 双流道流量计相对于单流道流量计在各流量下的精度值.计算公式为:

式中:1为单流道流量计在各种流量下的误差度,2为双流道流量计在各种流量下的误差度.
由表7的结果比较可知, 入口管道安装为半月双弯管的双流道流量计时, 在为2.5m3·h-1以及10m3·h-1时, 计量精度相对于单流道流量计分别提高了1.0940%和1.2058%, 而入口管道安装为双弯管时, 精度分别提高了2.1120%和2.2930%, 所有求得的Δ值均大于0, 说明双流道流量计相比单流道流量计抗扰流能力更好, 计量精度明显提高.

表7 双流道流量计相对于单流道流量计在各种流量下的测量精度提高值
7 结论
本文首先对分别安装直管、双弯管和半月双弯管入口管道的G16单流道超声波流量计进行仿真, 根据仿真结果求取流量值, 通过修正流量值并计算相对误差的方式, 验证了弯管对单流道流量计的计量精度产生较大影响, 然后针对此单流道流量计所存在的缺点, 建立G16型号双流道流量计, 进行同等条件下的仿真实验, 最后将数据进行分析对比得出如下结论:
(1)气流经过弯管会产生二次流、涡流等扰流, 造成流道内的流场分布不均匀, 给流量计测量精度带来影响.
(2)G16单流道超声波流量计在安装双弯管及半月双弯管情况下, 扰流影响较大, 流道内流场分布不均匀, 且超声波可覆盖范围小, 测量精度不够高, 相对误差大.
(3)G16双流道超声波流量计在安装双弯管及半月双弯管情况下, 扰流影响较小, 流道内流场分布较均匀, 超声波可覆盖范围增大, 测量精度较高, 相对误差减小.
(4)在流量为2.5m3·h-1以及10m3·h-1, 入口管道为半月双弯管时, 双流道流量计相对于单流道流量计测量精度分别提高1.0940%和1.2058%, 入口管道为双弯管时, 测量精度分别提高2.1120%和2.2930%, 而在其余流量下, 测量精度也均有所提高, 流量计计量效果得到有效改善.
[1] 黄瀛. 气体超声波流量计的研究[D]. 上海: 同济大学, 2009.
[2] 董雅琳, 裴小静, 刘涛, 等. 管道传输气体超声波流量计的新设计方法[J]. 控制工程, 2020, 27(12):2210-2218.
[3] 陈浩, 杨鸣. 超声波流量计双弯管流场整直问题的研究[J]. 现代科学仪器, 2019(4):5-9.
[4] 何明昊, 杨鸣. 超声波燃气表矩形流道的雷诺修正系数仿真研究[J]. 宁波大学学报(理工版), 2021, 34(2):25- 30.
[5] 陈红. 上游弯管对超声波流量计测量误差的影响[D]. 杭州: 中国计量学院, 2014.
[6] 杜晓泽, 刘胜祥. 时差法超声波流量计流量系数影响因素分析[J]. 工业计量, 2019, 29(2):14-15; 38.
[7] 张贤雨. 时差法超声波流量计产业化的关键技术研究[D]. 重庆: 重庆理工大学, 2014.
[8] 王雪峰, 唐祯安. 超声波气体流量计的管道模型仿真和误差分析[J]. 仪器仪表学报, 2009, 30(12):2612-2618.
[9] Synowiec P, Andruszkiewicz A, Wędrychowicz W, et al. Influence of flow disturbances behind the 90° bend on the indications of the ultrasonic flow meter with clamp-on sensors on pipelines[J]. Sensors, 2021, 21(3):868.
[10] 孙发君, 林惠阳, 刘自帅, 等. 基于CFD的超声波流体测量影响因素的模拟[J]. 科技和产业, 2020, 20(11): 240-246.
[11] 陈超. 家用超声波燃气表系统设计[D]. 宁波: 宁波大学, 2019.
[12] 汪晓凌, 黄江涛. 改善超声波气体流量计测量精度的方法研究[J]. 轻工科技, 2012, 28(9):124-125.
Effect of elbow on measurement accuracy of ultrasonic flowmeter and the improvement measures
LIU Yanan, YANG Ming*
( Faculty of Electrical Engineering and Computer Science, Ningbo University, Ningbo 315211, China )
When the fluid passes through the elbow of a channel, it is easy to produce secondary flow, eddy current and other complications, resulting in uneven velocity distribution in the channel. These complexities will affect the measurement accuracy of the flowmeter. In order to study the effect of turbulence on flowmeter, the measurement effect of G16 single channel flowmeter is investigated when the inlet pipe bears either double elbow or half moon double elbow by modeling and simulation. The flow error is calculated when the inlet pipe is straight pipe, so as to show the error was caused by the turbulence to the measurement result when the single channel flowmeter is installed with elbow. In order to reduce this kind of error, the model of G16 double channel flowmeter is established, and the simulation experiment is conducted under the same conditions. Finally, the obtained data are compared with the corresponding data of single channel flowmeter. The results show that the measurement accuracy of double channel flowmeter is higher than that of single channel flowmeter at each flow point. When the flow points are 2.5m3·h-1and 10m3·h-1and the inlet pipe is half moon double elbow, the measurement accuracy is improved by 1.0940% and 1.2058% respectively. When the inlet pipe is double elbow, the measurement accuracy is improved by 2.1120% and 2.2930% respectively. Compared with the single channel flowmeter, the double channel flowmeter greatly inhibits the disturbance caused by the elbow, and the measurement accuracy is thus significantly improved.
ultrasonic flowmeter; elbow; single channel; dual channel; numerical simulation
2021−05−18.
宁波大学学报(理工版)网址: http://journallg.nbu.edu.cn/
刘亚男(1996-), 女, 安徽六安人, 在读硕士研究生, 主要研究方向: 超声波气体流量计. E-mail: 1774596495@qq.com
通信作者:杨鸣(1963-), 男, 浙江宁波人, 研究员, 主要研究方向: 超声波计量及显微图像处理. E-mail: yangming@nbu.edu.cn
TH814
A
1001-5132(2022)03-0098-08
(责任编辑 章践立)

