基于灰狼优化算法的负荷模型参数辨识
郭 成,谢 浩,孟 贤,和 鹏,杨 蕾,王德林
(1.云南电网有限责任公司电力科学研究院,云南 昆明 650217;2.西南交通大学电气工程学院,四川 成都 611756)
电力系统数字仿真计算关系着电网的安全控制与动态分析,仿真结果的准确性对电力系统的调度运行与规划设计具有决定性影响,选取不合适的负荷模型进行电力系统仿真会使得仿真结果偏离实际,造成不必要的资金浪费甚至是错误的决策[1]。
总体测辨法是负荷建模中广泛使用的一种方法,包含2个步骤:①确定负荷模型[2-5];②对负荷模型进行参数辨识[6-7]。目前,对负荷模型进行参数辨识的方法主要有线性和非线性法。线性法主要有最小二乘法、卡尔曼滤波法等。非线性法主要有梯度法、随机搜索法和模拟进化法,主要思想是通过迭代找到一组最优的参数解,使得目标函数取得最优值。
随着人工智能的发展与推广,智能算法也越来越多地被应用到负荷建模技术研究中[8-14]。文献[10]在基本粒子群的基础上加入了S型惯性权重因子,提高了算法的遍历性与全局搜索能力,但是参数设置较为繁琐;文献[11]基于混沌优化算法增加了参数搜索范围自动缩小的功能,提高了算法的寻优速度;文献[12]针对蚁群算法在迭代寻优一定次数后容易出现早熟的问题,提出将混沌算法与蚁群算法混合,利用混沌算法的遍历性避免了早熟从而增强全局搜索能力,提高了模型辨识的精度;文献[13]通过分散协调控制与粒子群算法相结合,加速了种群的收敛速度,减少了负荷模型辨识的时间;文献[14]提出在微分进化算法的基础上借鉴遗传算法引入了移民策略,提高了算法的鲁棒性,但是算法的混合使得参数选取变得复杂。
灰狼优化(grey wolf optimization,GWO)算法是一种新型的群体智能优化算法,具有较好的全局收敛性、调节参数少、容易辨识等优点,目前已广泛应用于神经网络训练、最优控制策略等研究领域[15-16]。但鲜有学者将GWO算法应用于负荷建模研究当中。本文针对经典负荷模型,重点辨识感应电动机中灵敏度较高的参数,如定子绕组电抗、等值电动机负载率和电动机初始有功占比等,其余参数利用典型值代替;通过在PSD-BPA软件中建立电力系统仿真模型,以变电站母线处的扰动数据作为负荷建模的输入数据样本;利用GWO算法实现对目标函数的迭代优化并获得最优的负荷模型参数;最后,通过GWO算法与粒子群算法优化后的模型响应跟样本功率曲线对比,验证GWO算法能够提高负荷建模的准确性。
1 经典负荷模型
本文选取目前电力系统仿真计算中常用的由3阶感应电动机并联静态ZIP负荷构成的经典负荷模型,其对应的等值电路如图1所示。该等值电路中静态ZIP负荷以系统容量作为基值,而定子绕组电阻Rs、定子绕组电抗Xs、励磁电抗Xm、转子绕组电阻Rr和转子绕组电抗Xr以感应电动机额定容量作为基值。
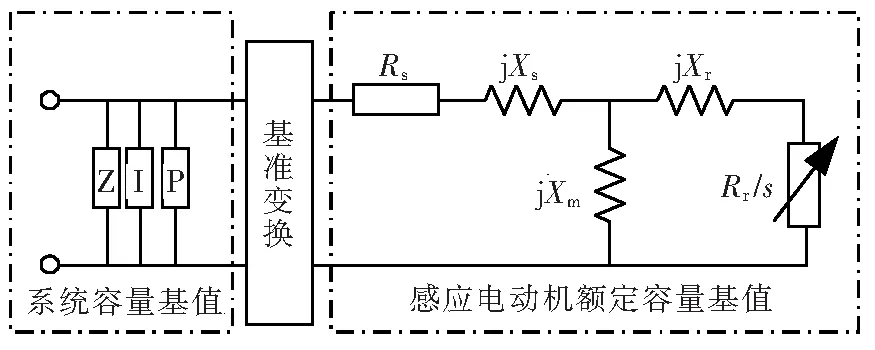
图1 经典负荷模型等值电路Figure 1 Equivalent circuit of classical load model
1.1 静态ZIP负荷和感应电动机数学方程
忽略频率变化的影响,静态ZIP负荷描述为
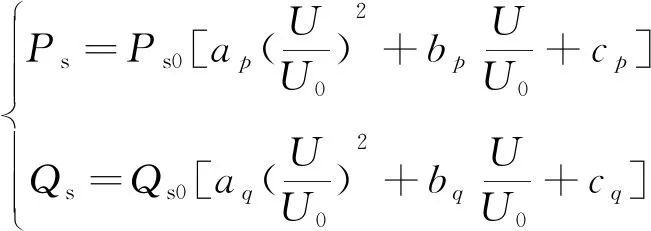
(1)
式中U0为负荷点的初始电压;Ps0、Qs0分别为静态ZIP负荷的初始有功、无功功率;ap、bp、cp、aq、bq、cq均为ZIP负荷的系数,各系数满足约束关系:
(2)
考虑机电暂态的3阶感应电动机负荷模型,采用电动机惯例,其方程描述为
(3)
(4)
(5)

式(3)~(5)中除了参数t、Tj为实际值以外,其余各参数均为标幺值,但电动机参数是以电动机额定容量为基值。文献[12, 17]为了使电动机额定容量对负荷初始功率的自适应变化,引入电动机负载率KL、电动机初始有功功率占比kpm和电动机额定容量与系统容量基值转换系数K,计算如下:
(6)
式中Pm0为等值电动机初始有功功率;P0为负荷初始有功功率;SMB为等值电动机额定功率;UB为系统和电动机电压基值;SBS为系统容量基值。
1.2 模型参数
根据CLM负荷模型的数学表达式,等值电动机待辨识的独立参数有10个:Rs、Xs、Xm、Rr、Xr、H2、H1、Tj、kpm、KL;静态ZIP负荷待辨识的独立参数有4个:ap、bp、aq、bq,一共有14个独立的待辨识参数。如果对这14个参数同时进行辨识,既影响辨识精度,还会增加计算时间。文献[18]指出等值电动机模型中定子电抗Xs、等值电动机负载率KL和等值电动机初始有功占比kpm灵敏度较高,其他参数可取典型值。
文献[19]给出了电力系统仿真计算时等值电动机的推荐参数:Rs=0、Rr=0.02、Xr=0.12、Xm=3.5、H2=0.85、H1=0。因此,本文采用文献[18]的辨识策略,选取的CLM负荷模型中共有7个重点待辨识参数,即
Y=[Xs,KL,kpm,ap,bp,aq,bq]
(7)
参数辨识过程中的目标函数为
(8)
式中J为适应度值;P、Q分别为实际母线有功、无功功率;Pm、Qm分别为等值电动机输出的有功、无功功率;Ps、Qs分别为静态ZIP输出的有功功率、无功功率;n为样本点的个数。
2 灰狼优化算法
2.1 算法原理
2014年,Marjalili根据自然界灰狼种群在狩猎过程中表现出来的等级制度,提出了操作简便、调节参数较少的GWO算法。在一个灰狼种群中,根据金字塔结构依次分为α、β、δ、ω共4级。在GWO算法中,最优解α灰狼、次优解β灰狼和再优解δ灰狼通过引导ω灰狼来完成捕食行为从而实现迭代寻优。其中包含3个阶段:包围、追捕、攻击。
1)包围。
设搜索空间为d维,灰狼包围猎物时距离更新位置为
X(i)={Xl(i)|l=1,2,…,d}
(9)
D(i)={(Dl(i)=
(10)
X(i+1)=XP(i)-A·D(i)
(11)
式(9)~(11)中i为当前迭代次数;X为灰狼的位置向量;XP为猎物的位置向量(以种群的当前最优解代入);D为灰狼与猎物的距离向量;A为灰狼对猎物的攻击系数,C为协同系数。其计算公式为
A=2m·r1-m
(12)
C=2r2
(13)
式中r1、r2为[0, 1]间的一维随机数;收敛因子m=2-2i/imax呈线性变化,imax表示最大迭代次数。
2)追捕。
GWO算法在迭代计算过程中,处于金字塔上层的α、β、δ灰狼有更多关于猎物位置的信息。因此,当猎物被包围后,追捕过程开始进行。此时,α、β、δ灰狼指导ω灰狼的位置更新:
(14)
(15)
(16)
式(14)~(16)中Xα、Xβ、Xδ分别为α、β、δ灰狼的位置向量;Dα、Dβ、Dδ分别为α、β、δ灰狼与猎物的距离向量;X1、X2、X3分别为α、β和δ灰狼的位置向量更新;X(i+1)为ω灰狼的位置向量更新;C1、C2、C3均为协同系数;A1、A2、A3均为灰狼对猎物的攻击系数。
3)攻击。
2.2 基于灰狼优化算法的负荷建模参数辨识
GWO算法应用于负荷建模参数辨识的算法流程如图2所示,主要计算步骤如下。
1)输入实测数据样本。本文需要的实测数据包含系统扰动情况下变电站的母线电压、电压相角、有功和无功功率。
2)设置灰狼种群规模、最大迭代次数、待优化参数维度,并初始化灰狼种群。
3)计算灰狼的适应度值。首先,根据每一只灰狼初始化CLM负荷模型中等值电动机的初始功率响应Pm0、Qm0和静态ZIP负荷的初始功率响应Ps0、Qs0,并计算式(3)微分方程中各状态变量的初值E′x0、E′y0和ω0;其次,运用4阶Runge-Kutta求解式(3)中每一时步的状态变量E′x(k)、E′y(k)、ω(k),并按式(5)计算每一时步等值电动机的功率响应Pm(k)、Qm(k),同时按式(1)计算每一时步静态ZIP负荷的功率响应Ps(k)、Qs(k);最后,通过目标函数式(6)计算灰狼种群的适应度值。文献[20]给出了详细的负荷模型初始化过程。
4)对灰狼种群进行适应度值排序,将最优解、次优解、再优解分别标记为α、β、δ灰狼。
5)检测当前迭代次数i是否满足设定的最大值,若满足则迭代结束,输出全局最优解;若不满足,则利用α、β、δ灰狼指导ω灰狼进行位置更新,并返回步骤3继续迭代。
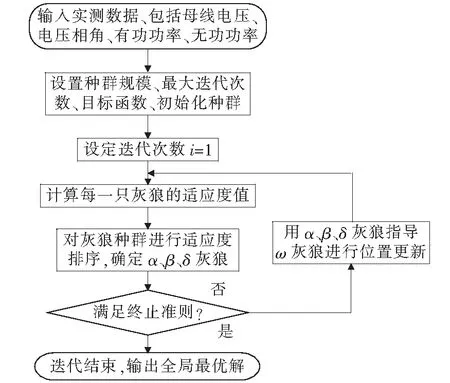
图2 GWO算法流程Figure 2 Flow chart of GWO algorithm
3 算例
为了检验GWO算法应用于负荷建模参数辨识的优越性,本文选取CLM负荷模型结构,分别使用GWO、PSO算法对待辨识参数向量Y的7个参数进行辨识。设置2种算法的种群数为40,最大迭代次数为100。
本文的三相、单相短路建模数据来源于PSD-BPA平台所搭建的3机9节点算例系统,如图3所示。母线2、A、B、C处均设置负荷为CLM模型,参考云南电网电动机负荷模型,设置等值电动机的初始参数:Rs=0.02、Xs=0.18、Xm=3.499、Rr=0.02、Xr=0.12、H2=0.85、H1=0、Tj=2.0、kpm=0.5、KL=0.011 6;静态ZIP参数:ap=1、bp=0、cp=0、aq=1、bq=0,cq=0。
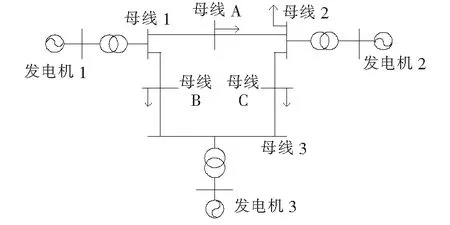
图3 3机9节点系统Figure 3 3-machine 9-bus power system
3.1 三相短路
扰动设置为母线A、2线路50%处在第5个周波发生三相短路故障,第10个周波母线A与母线2分别于故障相断开。记录母线2处的电压U、电压相角θ(如图4所示)以及有功P和无功Q。样本的时间长度均为1 s,步长为0.5个周波。

图4 三相短路情况下的母线2电压、相角曲线Figure 4 Voltage and phase angle curve of bus 2 under three-phase short circuit
分别以GWO、PSO算法优化的全局最优解作为仿真模型,并基于样本输入数据即母线2电压U、电压相角θ,输出仿真模型的有功和无功。基于样本数据的最优辨识结果如表1所示,可以看出,GWO算法对等值电动机灵敏度参数Xs、kpm、KL的辨识结果相对于PSO算法更接近于真值,基于GWO算法的适应度值J为0.041 4,优于PSO算法对应的适应度值(0.167 0),仿真时间减少了0.439 9 s,这表明采用GWO算法进行参数辨识具有更高的精度和效率。另外,静态ZIP负荷参数ap、bp、aq、bq的辨识结果出现较大偏差,其主要原因是参数自身的灵敏度较低,而非算法原因。
模型响应与样本功率曲线的拟合情况如图5所示,在三相短路情况下,2种算法迭代优化后的模型响应都表现出了较好的自描述能力,不过,从总体上比较,GWO算法优化后的模型拟合效果比PSO算法更接近样本曲线。
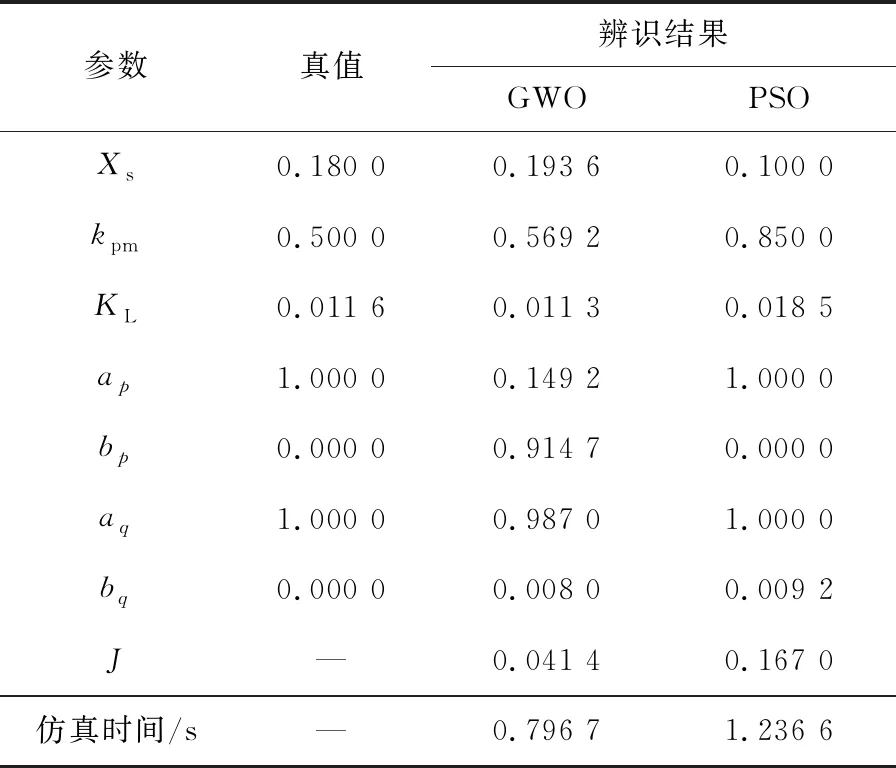
表1 三相短路情况下的样本数据最优辨识结果Table 1 Optimal identification results of sample
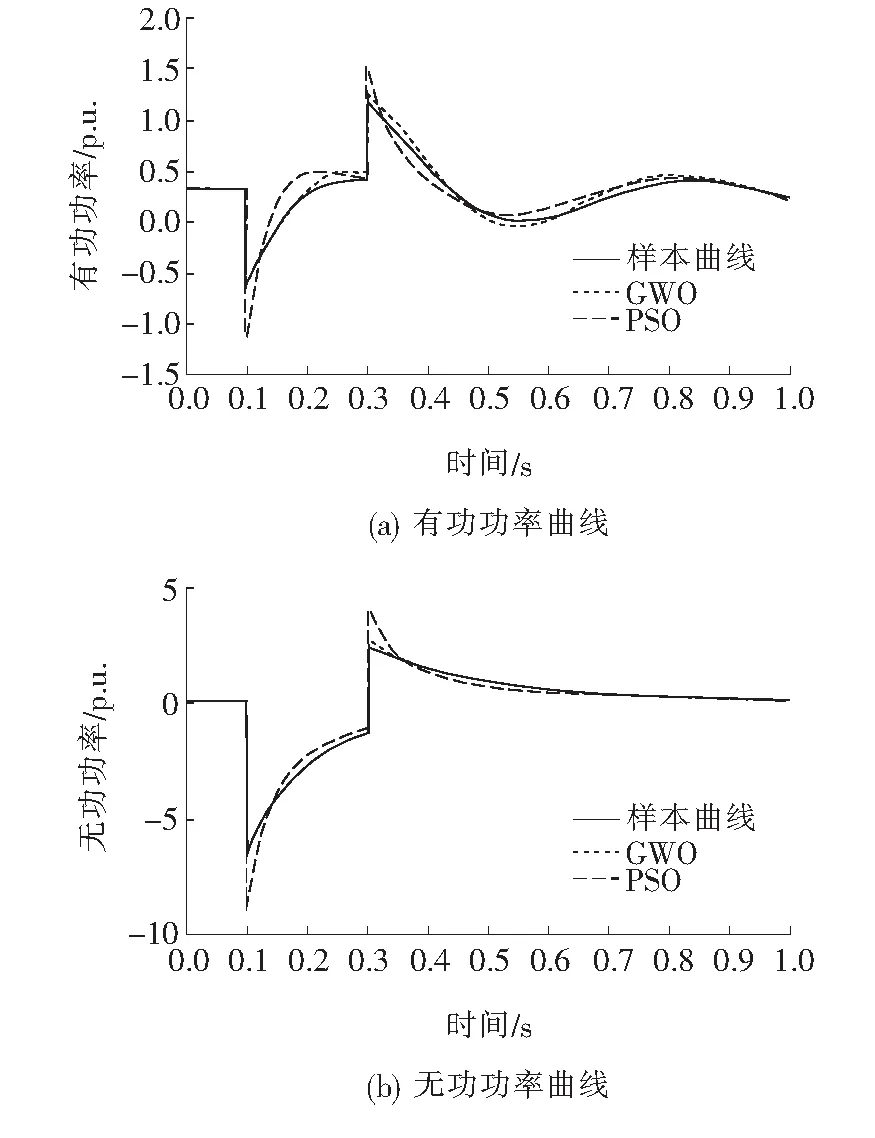
图5 三相短路情况下的模型响应与样本曲线对比Figure 5 Comparison of model response with sample curve under three-phase short circuit
迭代寻优过程中适应度值变化如图6所示,GWO算法迭代10次就收敛到最优稳定值,PSO算法迭代近17次才收敛到最优稳定值,同时,GWO算法整体适应值曲线比PSO算法更低,这说明了GWO算法具有收敛速度快、精度高的优点。
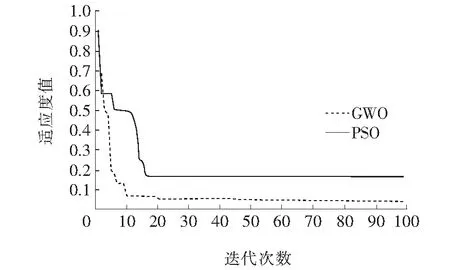
图6 三相短路情况下的适应度曲线对比Figure 6 Comparison of fitness curve under 3-phase short circuit
3.2 单相短路
扰动设置为母线A、2线路靠近母线A处在第5个周波发生单相瞬时短路故障,第6个周波母线A、2分别于故障相断开。记录下母线2处的电压U、电压相角θ(如图7所示)以及有功P和无功Q。样本的时间长度均为1 s,步长为0.5个周波。

图7 单相短路情况下的母线2电压、相角曲线Figure 7 Voltage and phase angle curve of bus 2 under single-phase short circuit
基于样本数据的最优辨识结果如表2所示,可以看出,GWO算法对参数Xs、kpm、KL的辨识结果相对于PSO算法更接近于真值,基于GWO算法的负荷建模J为0.020 5,优于PSO算法对应的适应度值(0.165 9),仿真时间减少了0.376 2 s,进一步表明了GWO算法在辨识精度、辨识效率上的优势。
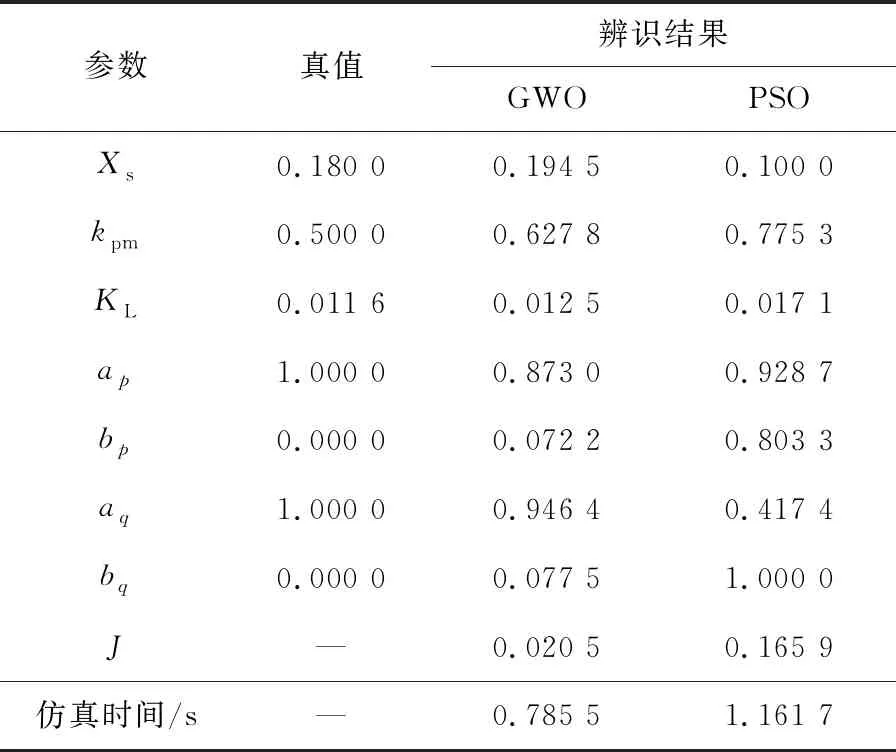
表2 单相短路情况下的样本数据最优辨识结果Table 2 Optimal identification result of sample data under single-phase short circuit
模型响应与样本功率曲线的拟合情况的拟合情况如图8所示,在单相短路情况下,GWO算法优化后的有功和无功功率响应均比PSO算法更接近样本曲线,表明了GWO算法的优越性;迭代寻优过程中适应度值变化如图9所示,PSO算法虽然比GWO算法更快收敛到最优稳定值,但是该算法陷入了局部最优,其适应度值远大于GWO算法优化后的适应度值。进一步验证了GWO算法全局寻优能力更强,辨识结果更精确的优点。
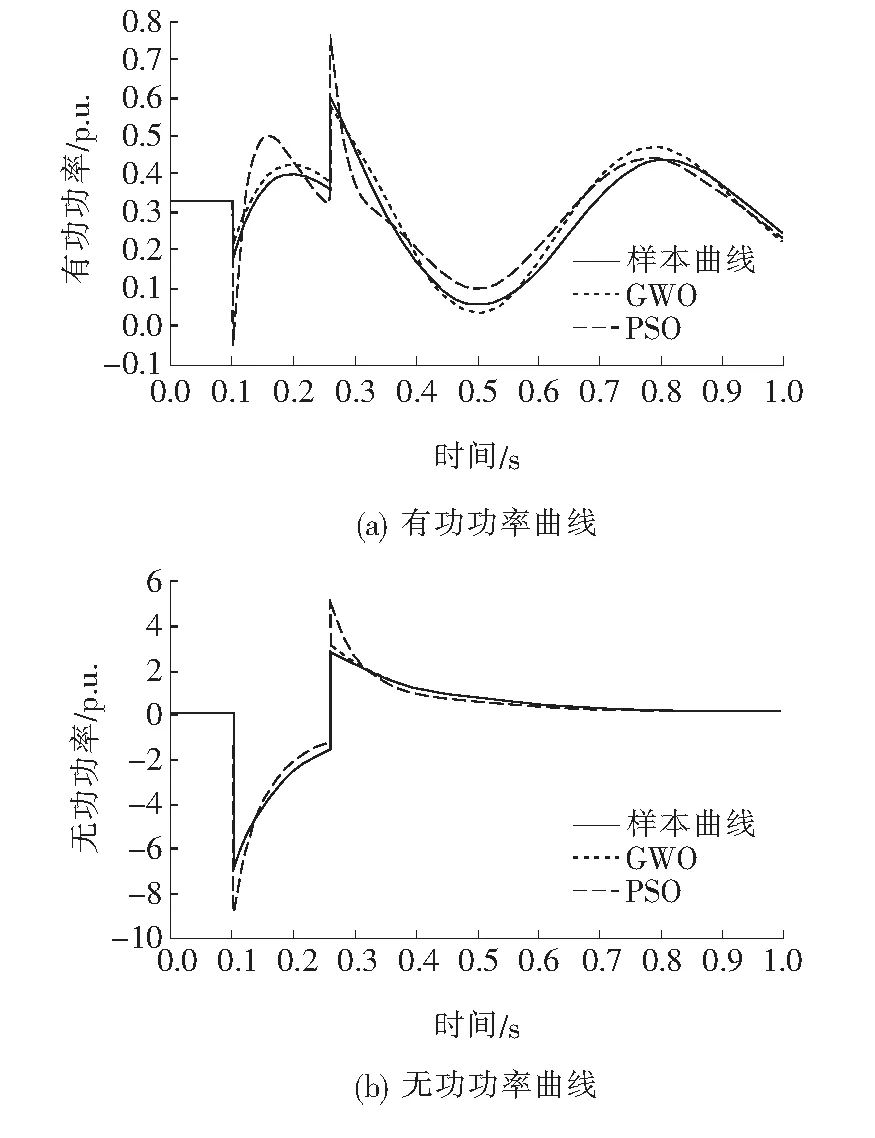
图8 单相短路情况下的模型响应与样本曲线对比Figure 8 Comparison of model response with sample curve under single-phase short circuit
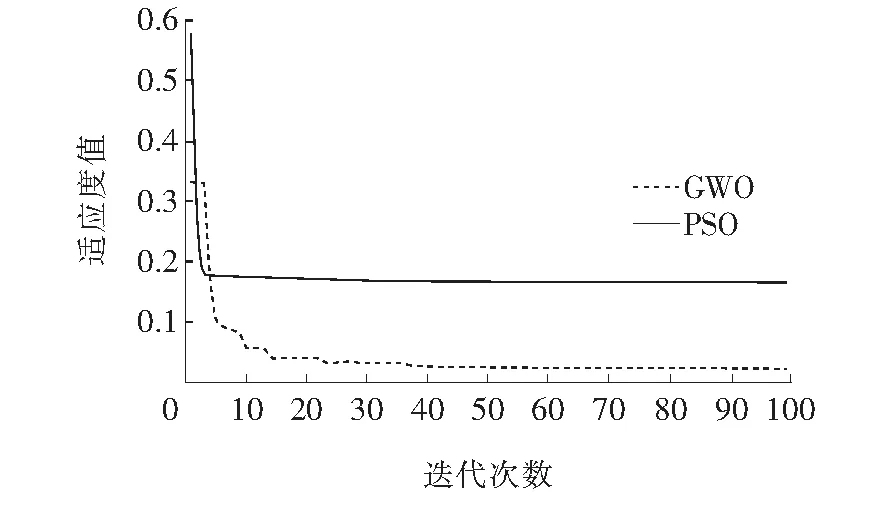
图9 单相短路情况下的适应度曲线对比Figure 9 Comparison of fitness curve under single-phase short circuit
4 结语
本文将灰狼优化算法应用于负荷建模参数辨识实践中,通过PSD-BPA中3机9节点系统中三相短路算例与单相短路算例中的样本数据进行建模,并引入粒子群算法进行了对比,得出结论如下:
1)基于CLM负荷模型,通过对重点参数向量Y进行辨识、其余参数选取为典型值的辨识策略,2种优化算法下的模型响应均与样本曲线较好的拟合,表明了该辨识策略的有效性;
2)基于负荷建模参数辨识结果,将等值电动机灵敏度参数Xs、kpm、KL的辨识值与真值进行对比,并比较了2种优化算法的适应度值,研究表明GWO算法在收敛精度上具有明显的优势,有利于提高负荷建模的准确性;
3)在种群数量、最大迭代次数一定的前提下,比较了2种优化算法的寻优时间及搜索到最优解时的迭代次数。研究表明灰狼优化算法具有更快的收敛速度,处理实际电网中采样频率更高的大量扰动数据能取得明显优势,具有良好的工程意义。

