电缆终端红外图像过热区域提取方法
夏湛然,杨 斌,郭浩然,徐小冰,周文俊,周承科
(1.国网湖北省电力有限公司武汉供电公司,湖北 武汉 430072;2.武汉大学电气与自动化学院,湖北 武汉 430072)
中国城市电网迅速发展,电力负荷不断上升,同时人们对供电可靠性和供电质量等提出了更高的要求[1]。由于电力电缆具备良好的电气、机械等性能,同时还具备环境友好优势,如今城市供电电缆化趋势愈发显著[2]。电缆终端作为电缆与其他电气设备的连接部件,是电力电缆的重要附件,但是由于制造、需要现场安装等因素,电缆终端也成为了电力电缆的薄弱环节[3]。大量实验以及实际观测均表明,当电缆终端存在缺陷,如金属连接部件接触不良、应力锥错位、绝缘层破损或内部介质存在杂质和气泡等,终端的运行温度往往高于相同运行条件下的正常终端[4]。因此,测量电缆终端的温度有利于及时发现异常发热现象并进行消缺。
红外测温技术由于具有非接触以及高效直观等优点,已成为电缆终端定期巡检的重要手段之一[5]。但是目前基于红外图像的电缆终端热状态诊断仍然依赖于人工,需要巡检人员根据自身经验,逐一判断图像中的诊断对象是否存在异常发热现象。过分依赖人工的诊断方式不仅费时费力,同时还可能由于巡检人员经验不足、视觉疲劳等造成漏判或者误判[6]。因此,针对电缆终端基于红外图像的智能化诊断研究具有重要意义。
许多团队针对电气设备红外智能诊断进行研究,提出了不同的过热区域提取方法。文献[7]针对电抗器,提出了基于遗传算法的模糊聚类方法;文献[8]针对建筑物内的配电箱,提出了最大稳定极值区域分割方法;文献[9]针对变压器,提出了分水岭结合K-means聚类方法。但是以上研究针对的对象均不是电缆终端,电缆终端的红外图像往往背景复杂,且发热区域在图像中所占面积较小,增大了准确提取的难度,因此,应用领域存在差异时无法保证上述图像处理方法的效果。
然而,目前与电缆终端红外诊断相关的研究较少,牛海清团队对瓷套电缆终端红外图像进行研究,先后提出了基于逐层最优基小波和贝叶斯估计的自适应[10]、考虑尺度间相关性的图像[11]以及改进的混合傅里叶—小波去噪方法[12],但是上述研究仅涉及电缆终端红外诊断的第1步,即图像预处理;文献[13-15]针对电缆终端红外诊断进一步研究:文献[13]提出一种结合Sobel算子和阈值分割的过热区域提取方法,该方法在图像背景简单时能够得到较好的分割效果,然而在图像背景复杂时,定位易出现失误,难以满足对定位精度的要求;文献[14]提出一种基于Radon和Fourier-Mellin变换的终端异常发热部位识别方法,该方法计算过程较为复杂,当红外图像分辨率较高时,计算量大,难以满足实时性的要求;文献[15]提出了Canny算法结合K-means聚类算法的疑似过热区域定位方法,文献中聚类数k由人工设定为固定值,然而实际上,不同的红外图像取得最佳分割效果的聚类数也不同,因此,文献[15]的方法虽然在部分图像上能够定位出关键区域,但是在其他图像上可能出现欠分割或过分割,造成定位错误,无法保证准确提取关键区域。
在实现电缆终端红外智能诊断的过程中,图像关键区域的提取至关重要,诊断对象和异常发热部位能否准确提取,很大程度上决定了后续缺陷识别的成败。本文针对电缆终端红外图像关键区域提取进行研究,提出一种包括图像预处理、电缆终端识别与定位以及像素点自适应聚类的红外图像过热区域提取方法。首先,利用基于最大后验概率估计的自适应小波阈值去噪方法进行图像去噪,提升图像质量;然后,利用深度学习网络Faster RCNN在图像中识别并定位出电缆终端;最后,利用均值漂移算法对终端像素点进行自适应聚类,并基于聚类结果提取出异常发热区域。将上述方法应用到实际拍摄的电缆终端红外图像中,验证本文所提方法的有效性。
1 电缆终端红外图像去噪
红外成像系统的成像效果同时受到拍摄对象材料发射率、背景与目标相似度以及探测距离等因素影响,因此相较于可见光图像,红外热像图图像质量较低,主要表现在对比度较低、细节分辨率较差以及信噪比较低[16]。图像质量低下可能造成后续关键区域定位出现偏差,因此,有必要先对红外图像进行去噪处理,改善图像质量。
小波阈值去噪作为红外图像去噪的常用方法,具有原理简单、易于实现等优点[17]。本文从电缆终端红外图像小波系数的分布特性出发,基于最大后验概率估计理论,提出一种不同分解尺度、不同方向上的局部自适应小波阈值去噪方法。
1.1 小波系数分布特性
常被用于描述电气设备红外图像小波系数分布的模型包括高斯、拉普拉斯分布[10-12]。本文提取电缆终端红外图像小波分解后的高频子带系数并绘制其分布曲线,计算实际分布曲线与上述2种统计模型的吻合程度,从而确定电缆终端红外图像小波系数的分布特性。
如图1所示,图1(a)为近似无噪的电缆终端灰度化图像,灰度化公式[18]为
I=0.299R+0.587G+0.114B
(1)
式中I为像素点灰度值;R为红外图像红色分量;G为绿色分量;B为蓝色分量。
文中采用Db4小波基,将分解尺度设置为3,对灰度图像进行小波分解,基于高频子带小波系数绘制得到的分布曲线如图1(b)~(d)所示。
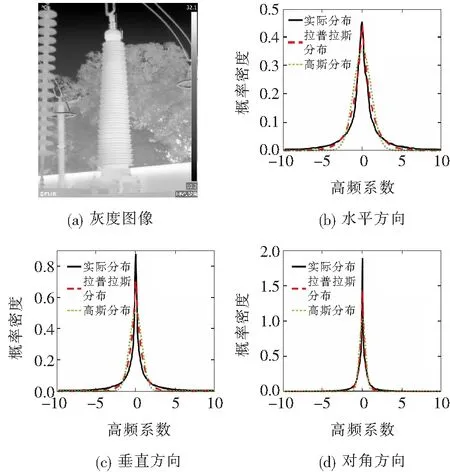
图1 电缆终端灰度图第1级高频小波系数分布特性Figure 1 Distribution characteristics of the first order high frequency wavelet coefficients of cable termination grayscale image
为了客观描述高频子带系数分布与统计模型的吻合程度,本文以确定系数R2作为评价指标,计算公式为
(2)
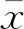
R2取值范围为[0,1],越接近1说明吻合程度越高[19],最终的计算结果如表1所示。结合图1、表1,可见在不同分解尺度、不同方向上,拉普拉斯模型与电缆终端红外图像高频小波系数分布的吻合程度更高。因此,相较于高斯模型,采用拉普拉斯模型对其小波系数进行描述更加合适。

表1 不同统计模型与高频小波系数分布曲线的拟合程度Table 1 The degree of fitting between different statistical models and the distribution curves of high frequency wavelet coefficients
1.2 最大后验概率估计
假设用Y、X、N分别表示电缆终端去噪前图像小波变换后、去噪后图像、高斯白噪声对应的小波系数,则
Y=X+N
(3)
本文根据最大后验概率估计[20],得到去噪后图像小波系数X的估计值:
(4)
根据贝叶斯定理,后验概率密度PX|Y(X|Y)[17]由先验概率密度计算得到,即
(5)
式中PN(Y-X)为噪声小波系数N的概率密度;PX(X)为去噪后小波系数X的概率密度;PY(Y)为去噪前小波系数Y的概率密度。
对小波系数分析可知,电缆终端去噪后图像的小波系数分布与拉普拉斯模型高度吻合,即X呈拉普拉斯分布;而高斯白噪声的小波系数N呈高斯分布。因此将式(5)代入式(4),得到X的最大后验概率估计:
(6)
式中 sgn为符号函数;σX为小波系数X的标准差;σN为小波系数N的标准差。
1.3 局部自适应小波阈值
(7)
式中Y为去噪前图像小波分解后的第1级对角方向高频子带系数。
σX采用最大似然估计法得到[22-23],文献[22-23]均以子带为单位进行计算,每个子带采用一个通用阈值。本文在此基础上进行改进,在各个子带中取方形窗口作为单位,在不同方向、不同分解尺度上得到σX的局部自适应估计:
(8)
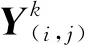
综上所述,结合式(6)~(8),最终得到基于最大后验概率估计的局部自适应小波阈值:
(9)
1.4 去噪效果对比与分析
为了分析不同小波阈值去噪方法得到的去噪效果,本文在电缆终端红外图像中添加不同程度的高斯白噪声,然后利用Matlab,分别基于传统的小波阈值去噪方法以及考虑小波系数统计特性的阈值去噪方法实现图像处理。电缆终端未去噪图像、传统阈值去噪效果(以启发式阈值Heursure为例)以及基于本文提出的自适应小波阈值去噪效果分别如图2(a)~(c)所示。

图2 不同小波阈值去噪效果Figure 2 Results of different wavelet threshold denoising methods
为了更加客观地描述去噪效果,本文利用均方误差(mean-square error, MSE)、峰值信噪比(peak signal-to-noise ratio, PSNR)作为图像质量的评价指标,MSE越小、PSNR越大,说明图像质量越高,即去噪效果越好[24]。
(10)
(11)
式(10)、(11)中m、n分别为红外图像对应矩阵的行、列数;f(i,j)为近似不含噪图像像素点(i,j)对应的灰度值;f2(i,j)为含噪图像对应的灰度值。
不同去噪方式在不同噪声水平下得到的MSE、PSNR如表2所示,可见传统小波阈值去噪方法虽然能够去除图像中包含的噪声,但是同时也破坏了图像的细节部分,导致去噪后的图像变得模糊;而基于小波系数统计特性的阈值去噪方法不仅能够有效去除噪声,同时还能较好地保存图像边缘等细节信息,去噪后的图像清晰度高。根据表2,可见相较于传统的小波阈值去噪方法,基于小波系数统计特性的阈值去噪方法得到的去噪图像MSE大幅度减小,同时PSNR明显增大,说明其对图像质量的改善程度明显优于传统的小波阈值去噪方法。在基于小波系数统计特性的阈值去噪方法中,本文提出的基于最大后验概率估计的局部自适应小波阈值去噪方法在不同噪声程度下均表现最佳,其去噪效果优于文献[22]、[23]的去噪方法。
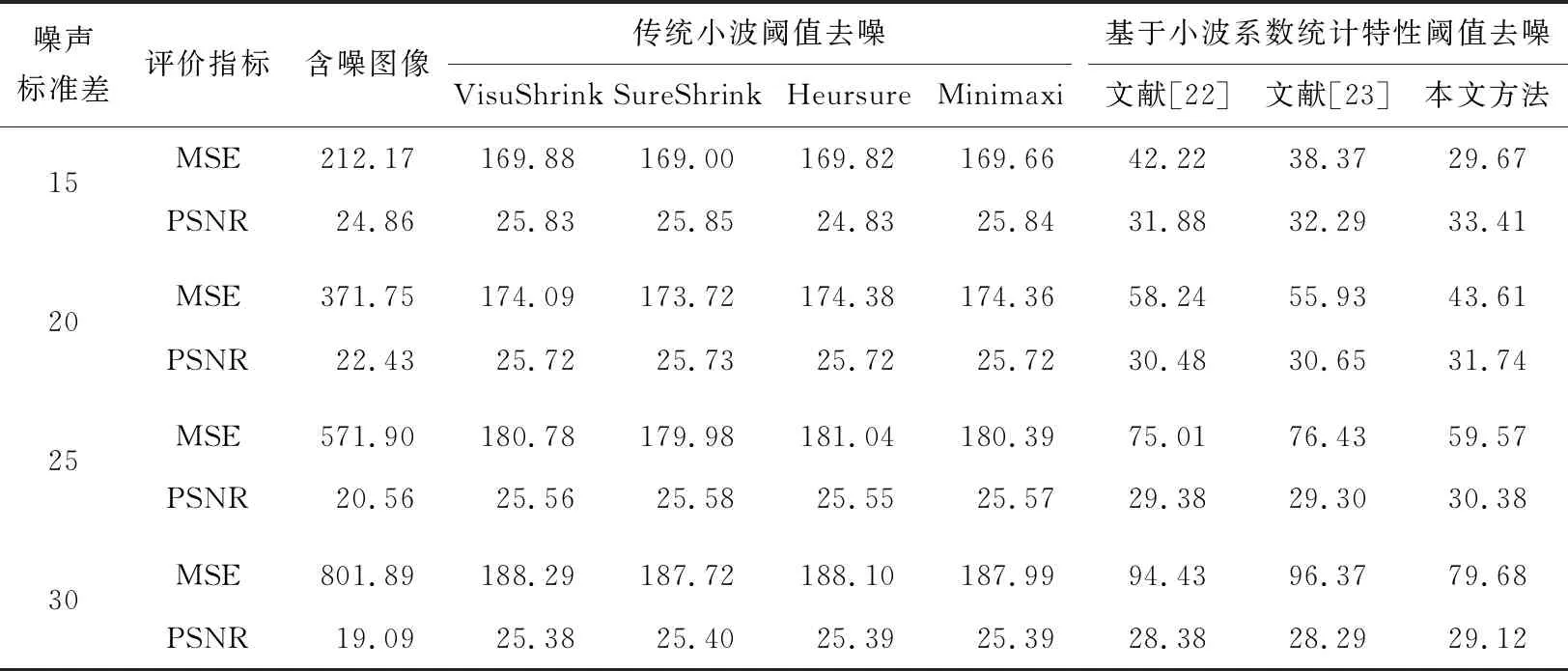
表2 不同小波阈值去噪效果对比Table 2 Performance comparison of different wavelet threshold denoising methods
2 电缆终端红外图像识别与定位
电缆终端红外图像往往背景复杂,如图3所示,图像中不仅包含电缆终端,还包含众多干扰物体,包括天空、植被等环境干扰,以及架空线、杆塔和绝缘子等非诊断对象的其他电气设备干扰。因此,在实现红外图像去噪后,本文通过在图像中识别并定位出电缆终端,以避免干扰信息影响后续的像素点聚类,防止过热区域提取出现偏差。

图3 电缆终端红外图像Figure 3 Infrared images of cable terminations
目前,基于灰度特征的模板匹配方法常被用于变电站电气设备图像的识别与定位[25]。此类红外图像多由固定的拍摄距离与拍摄角度获得,而模板匹配方法在模板与待匹配图像中诊断对象的尺寸以及角度一致时,匹配精度非常高,能够得到很好的匹配效果。但是电缆终端的红外图像大多由巡检人员在巡检过程手持热像仪拍摄所得,每一次的拍摄距离和拍摄角度均可能发生变化,这种情况下传统的匹配方法很难保证鲁棒性。另一方面,电缆终端红外图像尺寸较大,大多达到640×480,而传统的模板匹配方法需要在搜索窗口移动过程不断计算其与模板的相似程度,因此,应用于电缆终端红外图像时将导致计算量大、耗费时间长。
出于匹配精度以及耗时两方面的考虑,本文提出利用深度学习网络Faster RCNN实现图像中电缆终端的识别与定位。
2.1 Faster RCNN网络
Faster RCNN网络的结构以及工作原理如图4所示,该网络主要由卷积神经网络、区域建议网络、感兴趣区域池化层以及目标检测网络构成。
当输入电缆终端红外图像之后,一方面由卷积神经网络提取图像的高维特征形成特征图;另一方面由区域建议网络初步确定电缆终端在图像中所处的位置。具体如下。
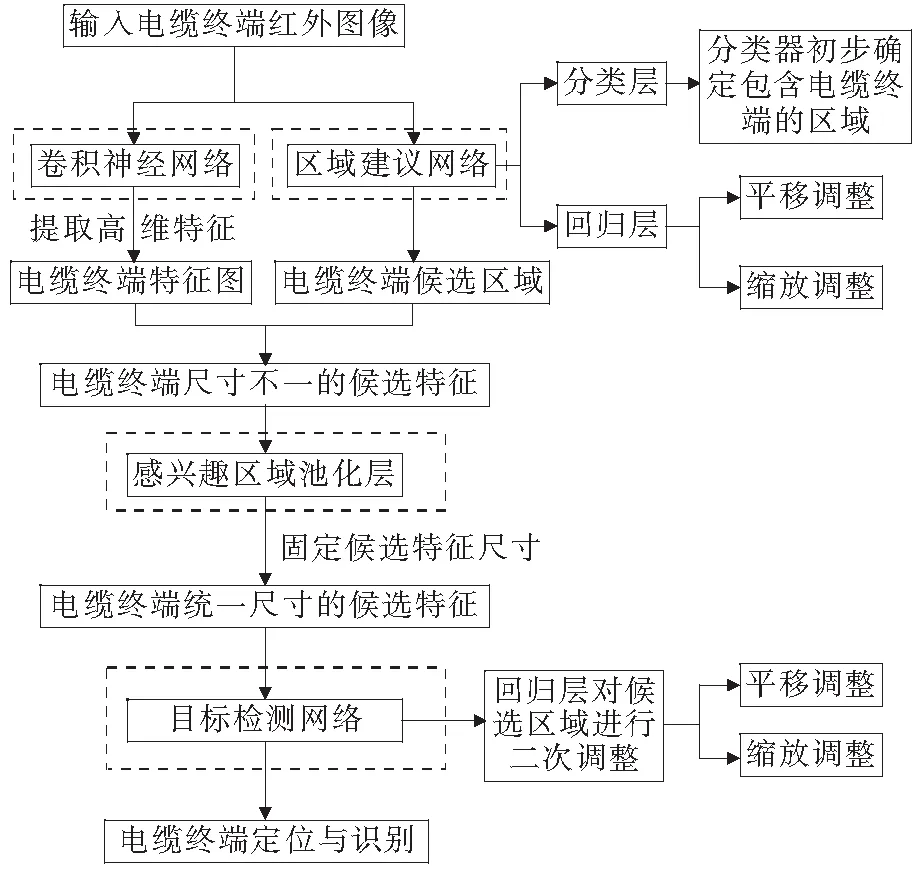
图4 Faster RCNN网络工作流程Figure 4 Workflow of Faster RCNN
1)卷积神经网络通过卷积核在红外图像上滑动检测到相应特征,即
(12)
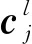
2)区域建议网络首先在分类层通过分类器初步确定包含电缆终端的前景区域,然后在回归层对候选区域进行平移和缩放,实现定位的初步调整,调整方式[26]为
(13)
式中x、y分别为候选框中心点的横、纵坐标;w、h分别为候选框的宽、高度;(Gx,Gy,Gw,Gh)为原始候选框的坐标;(G′x,G′y,G′w,G′h)为经过回归层调整的候选框坐标;dx(G)、dy(G)为平移参数;dw(G)、dh(G)为缩放参数。
将候选区域映射到特征图上,便得到了尺寸不一的候选特征,Faster RCNN网络将这些特征输入感兴趣区域池化层,通过最大池化处理将其转化为同一尺寸的候选特征,基于此,目标检测网络通过回归层对候选区域进行二次调整,完成红外图像中电缆终端的定位与识别。
2.2 测试结果与分析
本文利用含有一相或多相电缆终端的红外图像作为测试样本,如图5(a)所示。在Ubuntu软件上分别通过传统的模板匹配方法以及Faster RCNN网络实现图像中电缆终端的识别与定位,为了更好地体现测试结果,本文仅保留被识别为电缆终端的图像内容,而将其他像素点的R、G、B值均设置为零,最终结果如图5(b)、(c)所示。
本文对100张红外图像样本进行测试,如表3所示,结果表明:传统的模板匹配方法不仅用时长,且当拍摄角度不同或是拍摄距离不同导致图像中电缆终端尺寸发生变化时,还可能出现定位不完全(漏判,如图5(b2)所示)甚至定位错误(误判,如图5(b3)所示);而Faster RCNN网络检测结果不受拍摄距离与角度影响,具有良好的鲁棒性,保持极高的检测精度;同时相较于模板匹配方法,Faster RCNN网络用时大幅减少,在检测效率上也极具优势。

图5 不同方法识别定位结果Figure 5 Recognition and location results of different methods
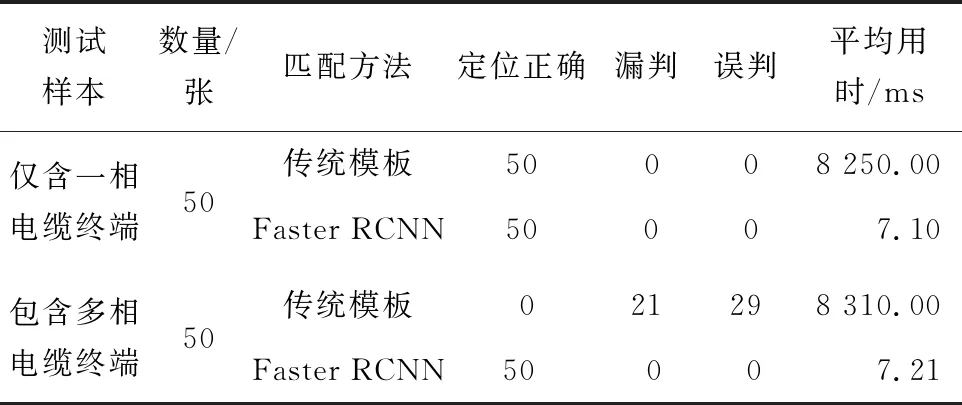
表3 不同识别定位方法结果对比Table 3 Performance comparison of different recognition and location methods
3 电缆终端红外图像过热区域提取
在识别并定位出红外图像中的电缆终端之后,本文进一步在电缆终端中提取出过热区域。由于红外图像像素点的灰度值能够反映温度高低,具体而言,灰度值越大,对应的温度越高,因此,本文基于灰度信息进行过热区域的提取。
均值漂移聚类作为一种无监督学习的方法,常被用于数据分析,该方法能够自适应地将数据点划分为不同的类别,同一类别的数据点具有相似的属性或特征,不同类别的数据点之间具有差别较大的属性或特征。因此,本文通过均值漂移聚类对电缆终端红外图像的灰度信息进行分析。
3.1 均值漂移算法
假设d维空间的样本点xi∈Rd,i=1,2,…,n,则x处的密度、密度梯度估计[27]分别为
(14)
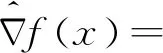
(15)
式(14)、(15)中h为聚类带宽;c为归一化常数;φ(·)为核函数。
令g(x)= -φ′(x),则式(15)可转化为
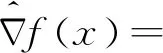
(16)
其中,
(17)
式中m(x)即为均值漂移向量,聚类中心根据m(x)进行迭代更新,即
xt+1=xt+m(x)
(18)
式中t为迭代次数;xt、xt+1分别为更新前、后的聚类中心。
均值漂移算法正是通过聚类中心的迭代更新实现对数据点的自适应分类,其聚类流程如图6所示,具体步骤:首先,该方法随机选取一个数据点作为初始聚类中心,并将与聚类中心距离小于带宽的所有数据点划分为同一类;然后,根据式(17)、(18)不断更新聚类中心,直到收敛;重复上述操作直到遍历所有数据点。
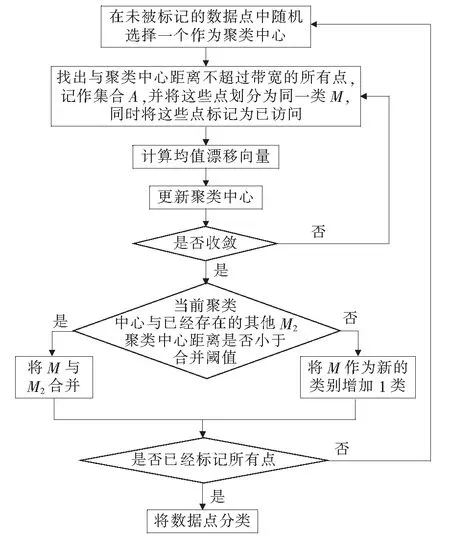
图6 均值漂移算法聚类流程Figure 6 Clustering process of mean-shift algorithm
3.2 像素点聚类效果与分析
本文利用不同部位存在异常发热现象的电缆终端红外图像进行测试。为了验证文中方法的有效性,基于Matlab,同时利用最常见的OTSU方法以及文献[15]应用的K-means聚类方法进行像素点的聚类,从而实现与文中方法的效果对比。
实现电缆终端识别与定位之后的红外图像如图7(a)所示;基于OTSU方法以及K-means聚类方法实现的过热区域提取效果分别如图7(b)、(c)所示;基于本文方法提取的异常发热区域如图7(d)所示。
根据测试结果,发现电缆终端常发生过热的区域,如连接金具、终端柱头以及应力锥对应的套管等,在终端整体中均只占较小的面积。而OTSU方法默认将像素点划分为2类,以类间方差最大为目标,自适应地计算出图像的分类阈值。当像素点的灰度值低于阈值时,认为该像素点属于背景,否则认为该像素点属于前景[28]。当这样的划分方式应用到电缆终端红外图像时,得到的分类阈值往往偏低,无法正确区分故障、正常运行区域。

图7 不同方法过热区域提取结果Figure 7 Extraction results of overheating regions by different methods
K-means聚类方法的效果明显优于OTSU方法。这是因为K-means聚类算法能够有效解决OTSU算法仅将像素点划分为两类的缺陷。该算法的工作原理为根据设定的类别数k,随机确定k个起始聚类中心,计算其余像素点与各聚类中心的相似程度,基于此将所有像素点划分为k类;之后以各类别均值替代原始聚类中心,迭代更新直到收敛[28]。但是不同的红外图像,其最适用的聚类数也不相同,而文献[15]中K-means聚类算法的聚类数根据人工经验设置为固定值,因此,难以保证针对所有电缆终端图像都取到恰当的聚类数。
而均值漂移算法能够根据不同的图像,自适应选择最合适的聚类数,解决K-means聚类算法需要人为设定聚类类别的问题。在测试中均值漂移算法能够准确且完整地提取出电缆终端存在异常发热的区域,效果优于OTSU方法与K-means聚类算法。
4 结语
本文针对电缆终端红外图像,提出了一种包括图像预处理、电缆终端识别与定位以及像素点自适应聚类的过热区域提取方法。首先,通过基于最大后验概率估计的自适应小波阈值去噪方法实现图像去噪,测试结果表明:相较于传统的小波阈值去噪以及基于小波系数统计特性的其他阈值去噪方法,本文方法在不同噪声水平下均取得最好的去噪效果,使得电缆终端红外图像质量得到有效改善;然后,利用深度学习网络Faster RCNN识别并定位出图像中的电缆终端,有效解决了传统模板匹配方法应用在电缆终端时存在的耗时长、鲁棒性差等问题;最后,基于均值漂移算法进行终端像素点的自适应聚类,测试结果表明:本文方法能够有效区分故障区域与正常运行区域,完整并且准确地提取出过热区域。

