基于双注意力机制优化CNN架构的GIS局部放电模式识别
王彦彪,陈振勇,郭文萍,王宗宝,黄银汉
(1.国网甘肃省电力公司白银供电公司,甘肃 白银 730900;2.国电南瑞南京控制系统有限公司,江苏 南京 211100)
局部放电(partial discharge,PD)是反映气体绝缘开关设备(gas insulated switchgear,GIS)内部绝缘状况的重要指标之一[1-2]。由于不同缺陷引发的局部放电现象和机理不同,其对内部绝缘造成的劣化程度各异,因此,有必要对GIS内部出现的局部放电信号进行识别,以保证GIS的安全稳定运行。
局部放电信号识别可以分为特征提取和分类器识别两步,其中信号的特征提取是识别成功与否的关键。针对局部放电信号的特征提取,常采用统计参数法[3-4]、分形特征[5]、图像矩特征[6]、纹理特征[7]等,但是通过这些方法提取得到的特征数量较多,造成特征空间维度较高,不仅有严重的特征冗余,还给分类器带来负担。同时,上述的特征提取方法需要大量的专家经验和先验知识,在缺乏理论背景的前提下,较难提取出合适的特征。
目前,随着深度学习在图像识别、语音识别、语义分析等领域的成功应用,基于深度学习实现端到端的故障智能化诊断逐渐成为研究热点。如:文献[8]采用卷积神经网络对直流交联聚乙烯电缆的局部放电类型进行识别;文献[9]通过卷积神经网络对5种局放缺陷类型的时域波形图像进行识别;文献[10]基于卷积神经网络对高压电缆局部放电模式进行识别。可见,卷积神经网络(convolutional neural network, CNN)架构作为目前应用最为广泛且成熟的深度学习架构已被应用在各类电气设备的故障诊断中。然而传统CNN架构存在问题[11-12]:①网络卷积、池化时没有考虑各层结构中不同特征重要性,徒增网络计算量,影响网络性能;②网络池化往往采用平均池化或最大池化,针对不同深度特征缺乏池化方式的科学合理选择。
针对上述问题,在CNN架构的基础上,本文提出双注意力模块优化的CNN架构,即在传统卷积、池化过程中加入包含通道和空间注意力机制的模块,以解决不同通道特征和相同通道不同位置特征的重要性选择、加权问题。据此,提出一种基于双注意力机制优化的GIS局部放电信号识别方法,通过超高频和超声波检测法对不同缺陷局部放电信号进行采集,构建由超高频局部放电谱图图像特征和超声信号格拉米角场密度分布组成的特征空间,基于所提方法完成数据深层特征提取和类型识别。
1 局部放电实验
1.1 样本制作
基于GIS制造过程中可能因人为失误而造成的4种常见缺陷建立实验模型[13-14],如图1所示。
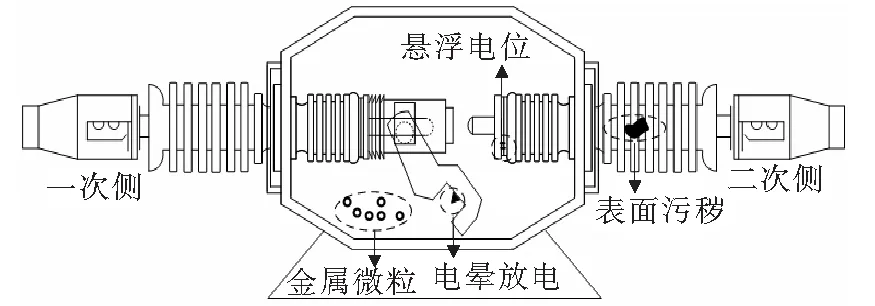
图1 典型缺陷试样Figure 1 Typical defect sample
1)表面污秽。在二次侧瓷套内导体表面含油脂。
2)金属微粒。GIS罐中含金属微粒,微粒尺寸约为5 mm×3 mm×1 mm。
3)电晕放电。通过在操作手柄连接杆上焊接突起实现,突起尺寸约为5 mm×5 mm×2 mm。
4)沿面放电。通过内部金属环的磨损缺陷模拟,缺损深度为2 mm,长度为10 mm。
1.2 局部放电测试平台及加压方式
局部放电测试平台如图2所示,变压器为无晕试验变压器(YDTW-25/100),保护电阻为10 kW保护性水阻。采用Tektronix DPO7104高速数字存储示波器记录PD波形,超高频探头的检测频段为300~1 500 MHz,超声波传感器检测中心频率为40 kHz。实验在高压屏蔽大厅进行,针对无缺陷GIS的加压测试背景噪声控制在3 pC左右。

图2 局部放电测试平台Figure 2 Partial discharge test platform
根据高压开关设备试验标准IEC 62271-203,测试设备必须在耐受电压下承受1 min的最大应力,在此期间发生的局部放电信号应被忽略,1 min后外施电压降至PD测试电压。GIS额定电压Ur为15 kV,在45 kV耐受电压下施加1 min的升压,然后,将电压降至1.2Ur/1.73=10.4 kV以测量局部放电。每次测量完成后将实验设备闲置1 h,然后再测量下一组数据。GIS局部放电过程中的电压施加曲线如图3所示。
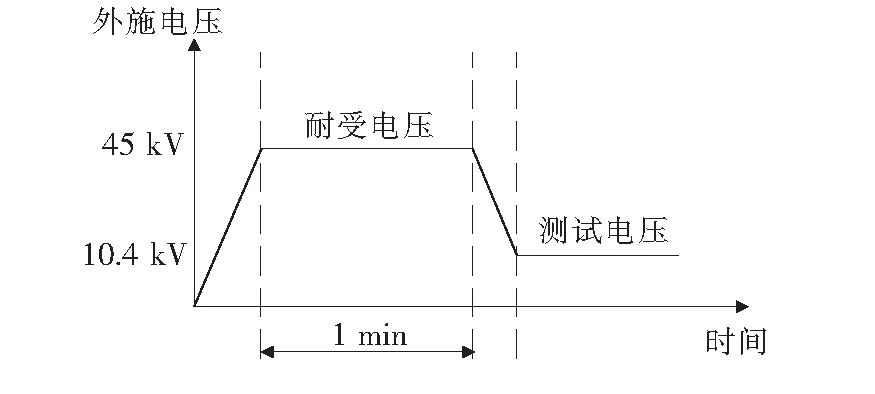
图3 外施电压Figure 3 Applied voltage
1.3 局部放电信号
4种典型缺陷样本的超高频信号PRPD谱图如图4所示,可见不同缺陷下测得的PRPD谱图形态各异,可将其作为分类算法输入进行识别,为后续算法识别便捷,将数据进行归一化处理,使信号幅值分布在[0,1]范围内。采用统计、图像特征等对局部放电PRPD谱图进行特征提取,这些方法均需要较为丰富的专业背景,难以满足电力设备智能诊断的需求[15]。对采集的PRPD谱图进行预处理后,本文采用后续深度学习算法对其进行深度特征提取,免去人工特征提取步骤,简化诊断流程。
归一化处理后的4种典型缺陷样本超声波信号如图5所示,采样频率为40 kHz,采集时间为30 ms。由于采样点为与时间相关的一维序列,且长度为104样本点,若将其直接作为网络的输入,不仅会导致网络运行缓慢,还存在数据点丢失的情况。据此,本文将测得的时序信号采用格拉米角场(gramian angular field, GAF)密度表示[16-17],如图6所示,将数据映射到极坐标系中,而不是笛卡尔坐标系。

图4 超高频局放信号PRPD谱图Figure 4 PRPD patterns of UHF PD signal

图5 超声波局放信号Figure 5 Ultrasonic PD signal

图6 超声波局放信号的GAF密度分布Figure 6 GAF density distribution of ultrasonic PD signal
GAF图像有2个优点:①极坐标系保持笛卡尔坐标系不存在的绝对时间关系;②该方程能够产生唯一的映射。因此当数据反演时,GAF图像产生的变换是无损的[18],其主要显示数据点之间的时间相关性,同时保留了空间位置信息。
基于局部放电实验平台,针对每类缺陷,本文通过超高频检测法采集局部放电PRPD谱图200张,通过超声波检测法采集局部放电信号150条。
2 双注意力机制优化的CNN架构
2.1 通道注意力模块
通道注意力模块(channel attention modulem, CAM)通过加权不同通道间的相关性生成特征图,由于每个通道都可被看作一个特征检测器,该机制可以使模型更加关注有效信息的通道特征[19]。由于卷积运算只能在局部空间中进行,CAM很难获得足够的信息来提取不同通道间的关系,因此,将通道上的整个空间特征编码为全局特征,使用全局平均池化和全局最大池化来实现。整体思路[20]:将输入特征分别经过全局平均池化和全局最大池化后获得全局描述特征;再由2层结构的感知器进行特征连接,将由多层感知器输出的特征进行元素加权、融合;最后,将Mc特征和输入特征F进行元素相乘得到最终的特征,整体提取过程如图7所示。
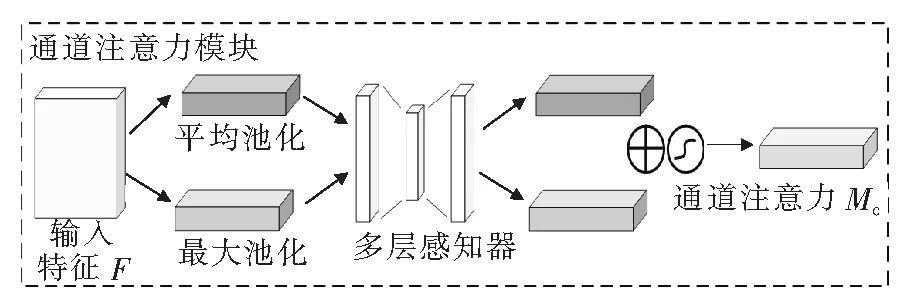
图7 通道注意力模块Figure 7 Channel attention module
平均池化和最大池化的过程分别如下:
(1)
Fmax=max(F(i,j))
(2)
式(1)、(2)中Favg、Fmax分别为具有输入特征映射F的全局平均和全局最大池化结果;H、W分别为输入特征的高、宽。
通道注意力Mc的计算公式为
Mc(F)=
(3)
其中,W0、W1为多层感知器中的全连接结构,W0层起降维作用,W1层将输入特征恢复至原始尺度。为了降低模型的复杂度,采用含2个全连接层的瓶颈式结构σ表示Sigmoid操作。
2.2 空间注意力模块
与通道注意力机制不同的是,空间注意力机制更加关注目标特征位置,利用特征的空间关系生成空间注意力图[21],空间注意力模块(spatial attention module, SAM)整体流程如图8所示。计算整体思路[22]:首先,对输入特征F的通道进行轴向全局平均池化和全局最大池化;然后,将池化结果连接生成一个有效的特征描述符;最后,经过卷积降维生成空间注意力图Ms(F)。计算过程为
(4)
其中σ为Sigmoid操作,7×7为卷积核大小。通过空间注意力图可反映输入特征需关注或抑制的位置。
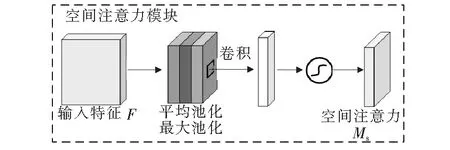
图8 空间注意力模块Figure 8 Spatial attention module
2.3 整体网络架构
为了提高局部放电识别模型的性能,在特征提取网络中加入CAM、SAM。通道注意力模块分别采用平均池化和最大池化压缩特征映射的空间维数,空间注意力模块分别沿信道维度应用平均、最大池化。
注意力模块是一个轻量级的通用模块,可以集成到CNN中进行端到端的训练。在5层CNN架构的基础上,本文引入双注意力模块进行优化,整体结构如图9所示,图9(a)为单个CSAM结构,对于每个卷积块的特征图A,添加2个连续的注意力模块(CAM、SAM),并将处理后的特征B传递给下一个卷积模块;图9(b)为含双注意力模块的CNN架构,输入为局部放电PRPD谱图和GAF图像,通过5层CSAM结构进行深层特征提取,再经Flatten层将多维输入一维化,最后由2层全连接层输出至Softmax分类识别。

图9 整体网络架构Figure 9 Overall network architecture
所提网络架构的结构参数如表1所示,网络输入尺寸设定为256×256×1;M1~M5为CSAM结构,分别含2个3×3×32、3×3×32、3×3×64、3×3×64、3×3×128的优化卷积块。在Flatten层将特征图矢量化为1×1×8 192,实现从卷积层到全连接层的过渡;然后,将8 192个元素分别输出至含150、4个神经元的双层全连接层;最后,将全连接特征输出至Softmax进行局部放电类型识别。
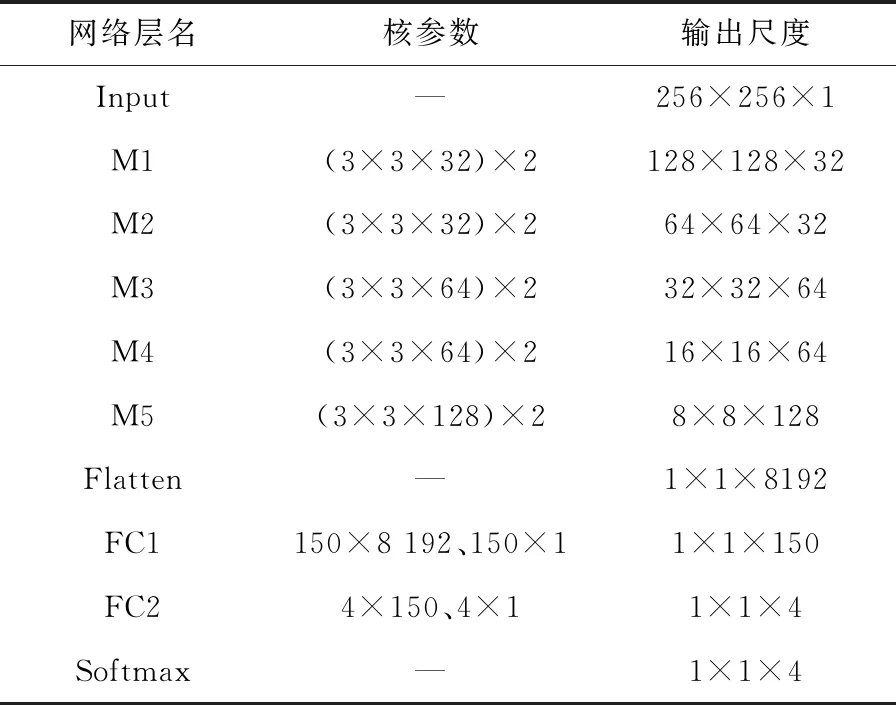
表1 网络参数Table 1 Network parameters
3 结果分析
通过十折交叉验证对GIS局部放电类型[23-24]进行识别,即将局部放电数据集分成10份,依次将其中9份做训练,其余1份做验证,10次结果的均值作为对算法精度的估计。本文分别对网络训练损失函数值、识别准确率及F1指数进行分析,探讨不同特征输入时的网络性能以及不同网络在相同特征输入时的性能。
3.1 网络输入对比分析
针对不同特征输入时的网络性能,本文对4种情形进行讨论:
情形1 网络输入为局部放电PRPD谱图时采用CSAM-CNN识别模型;
情形2 网络输入为局部放电时序信号时采用CSAM-CNN识别模型;
情形3 网络输入为局部放电格拉米角场密度分布时采用CSAM-CNN识别模型;
情形4 网络输入为局部放电PRPD谱图及格拉米角场密度分布时采用CSAM-CNN识别模型。
不同网络输入时的损失函数值如图10所示,在网络收敛速度方面,情形4在40步左右逐步收敛,情形1/2/3在迭代前期有较小的振荡,80步左右趋于收敛;在网络收敛方面,loss稳定值大小依次为情形4<1<3<2。综上,网络输入为局部放电PRPD谱图及格拉米角场密度分布时的网络收敛较快,且保持较低的网络损失值。

图10 网络输入对loss值影响分析Figure 10 Influence analysis of network input on loss value
基于十折交叉验证的识别准确率如表2所示,识别准确率反映了训练完成网络对测试集数据的识别程度。从表2可以看出,与其他情形比较,情形4的平均准确率最高,为97.57%,而情形2的平均准确率最低,为66.79%。说明采用超声波局部放电时序信号作为网络输入不仅使网络迭代速度降低,还降低了识别准确率。而融合超高频局放PRPD谱图和超声波局放格拉米角场密度分布的数据特征具有更好的故障表征能力,能够较为全面的反映局放类型。

表2 识别准确率Table 2 Recognition accuracy %
基于十折交叉验证的F1指数结果如表3所示,F1指数的计算公式为
(5)
其中,TP表示预测为真,实际也为真;FP表示预测为真,实际为假;FN表示预测为假,实际为真。F1指数通过实现精确率和召回率间的平衡,从而能够更加客观的描述网络预测性能,其值越接近1说明性能越好。从表3可以看出,情形4的F1指数最接近1,且均高于其他情形,说明情形4的网络综合性能最佳。
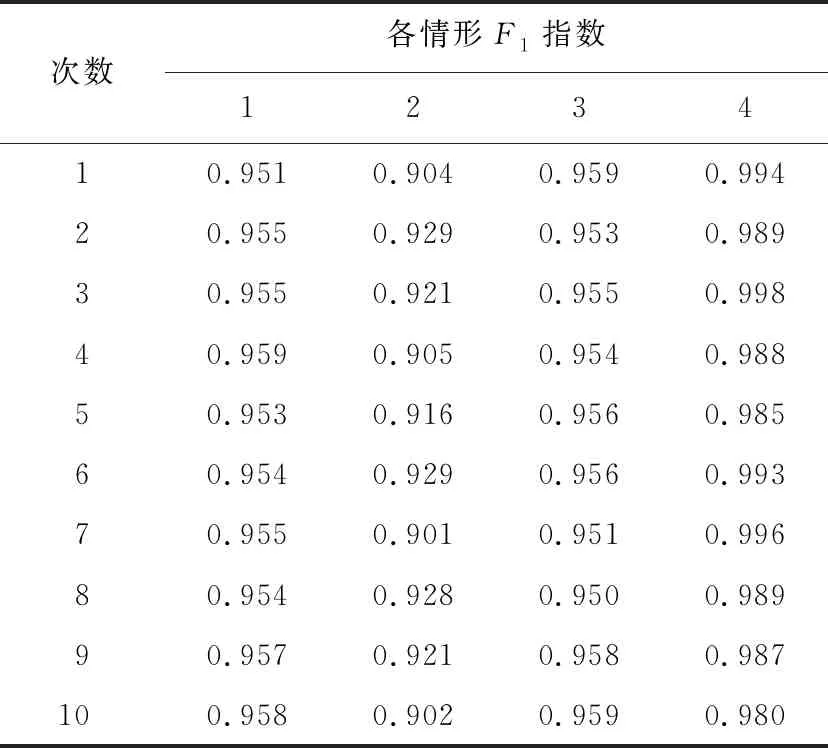
表3 F1指数Table 3 F1 index
3.2 不同深度学习算法对比分析
针对不同网络在相同特征输入时的性能,本文对2种情形进行讨论:
情形5 网络输入为局部放电PRPD谱图及格拉米角场密度分布时采用栈式自编码器(stacked auto encoder, SAE)识别模型;
情形6 网络输入为局部放电PRPD谱图及格拉米角场密度分布时采用卷积神经网络识别模型。
采用不同深度学习网络时的损失函数值如图11所示,在网络收敛速度方面,3个网络均在40步左右趋于稳定,有较快的收敛速度;在网络收敛方面,loss稳定值大小依次为情形4<6<5。综上,采用CSAM-CNN识别模型能够保持较低的网络损失值。
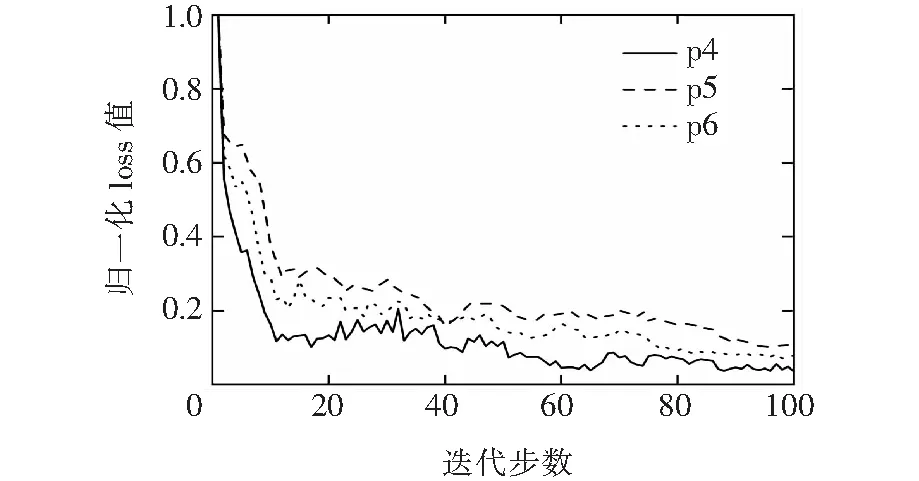
图11 网络类型对loss值影响分析Figure 11 Influence analysis of network type on loss value
识别准确率、F1指数分别如表4、5所示,可以看出,在同一特征输入下,采用CSAM-CNN识别模型不仅在识别准确率上高于其他模型,而且在F1指数上也更接近1。说明与其他常用深度学习相比,CSAM-CNN具有更快收敛速度、更低损失函数值,同时故障识别率更高、网络综合性能更佳。
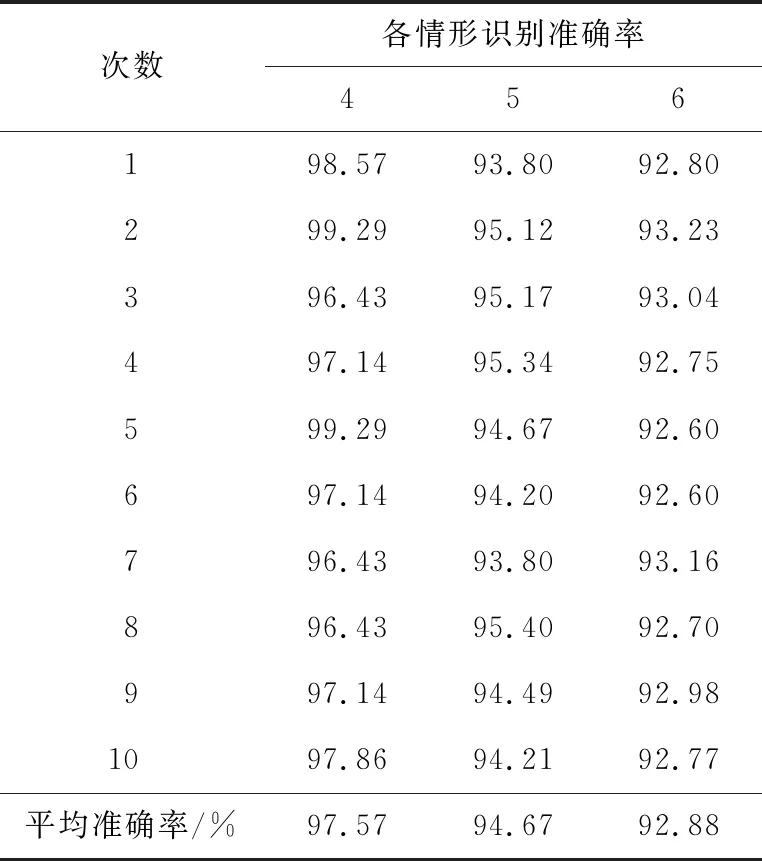
表4 识别准确率Table 4 Recognition accuracy %

表5 F1指数Table 5 F1 index
4 结语
针对GIS局部放电信号进行准确、高效识别,提出了一种基于双注意力机制优化CNN的GIS局部放电信号模式识别方法,得出结论:
1)当采用融合局部放电PRPD谱图和格拉米角场密度分布图作为CSAM-CNN识别模型输入时,能够达到97.57%左右的识别准确率,高于采用单一特征时的模型识别率;
2)在同一特征输入时,采用CSAM-CNN识别模型具有更快收敛速度、更低损失函数值,同时故障识别率也更高、网络综合性能更佳。

