复杂地质条件下瓦斯含量精准预测研究与系统开发

廖 巍

(1.煤矿安全技术国家重点实验室，辽宁 抚顺 113122；2.中煤科工集团沈阳研究院有限公司，辽宁 抚顺 113122)

瓦斯含量是瓦斯地质信息核心参数，研究瓦斯含量赋存规律是绘制瓦斯地质图的基础条件[1-3]。由于受到专业壁垒的限制，缺乏运用数学的手段对瓦斯含量值进行深度分析，无法运用计算机对大量复杂地质与瓦斯防治措施等数据资料进行全面深入分析[4-7]。传统瓦斯地质分析多为静态评价结果，不能动态实时地从设计、掘进到回采整个过程对工作面进行危险性评价分析，数据多以文字形式表达，缺乏对空间数据的可视化展示及分析，无法精准预测瓦斯含量[8-12]。此外，在研究瓦斯含量赋存规律时，一般采用简单的一元线性分析模型，然而复杂地质条件下瓦斯的赋存受多种因素影响，并且随着采掘活动的进行，瓦斯也会发生二次分布，因此无法获取准确的预测结果[10，13-15]。根据有限的样本点预测整个采区的瓦斯含量分布，一直困扰着科研工作者，国内外不少学者根据非煤矿研究实践引入了克里金、反距离插值等算法[16-19]，相对而言，较线性预测模型有大幅提升，然而受限于数学知识以及现场实践经验，预测结果的精准性亟待提高。笔者在总结前人的基础上，将泛克里金插值算法与小回沟地质条件相结合，对该矿瓦斯含量预测模型进行了深入研究，并根据相应成果为小回沟开发了一套动态瓦斯地质预测系统，实现了该矿井瓦斯地质图动态生成与综合分析，并完成瓦斯含量精准预测预报与瓦斯地质的信息化与精准化管控，为瓦斯防治提供决策性依据与辅助手段。

1 算法模型研究

1.1 预测算法分析

煤层地质条件复杂多变，瓦斯含量空间特征呈现非平稳随机分布，采用泛克里金插值算法反演小范围瓦斯赋存规律具有较高的可靠度[20-22]。根据煤矿地质构造分布状况划分地质单元，采用泛克里金插值方法准确度较高，假定瓦斯含量为区域化变量P(x)，则：

E[P(x)]=m(x)

(1)

式中，m(x)为在给定点x为中心的邻域内任一点漂移。

式中，p为样本点数量；fq(x)为已知函数；aq为未知系数。

为了确保估计量与实际值偏差在可接受的误差范围内，采用无偏最优估计方法进行优化，根据拉格朗日乘数法原理，推导出估计量P(x)的泛克里金方程为：

式中，x，xi为相应样品点；n为样品点数量；k为无偏性条件约束等式数目；μq为拉格朗日乘数；fq(xi)为已知函数；λj为权重系数；C(xi，xj)为相应样品点的协方差；C(x，xj)为相应样品点的协方差。

1.2 泛克里金算法模型研究

指定的瓦斯地质单元内，样本点的期望虽然存在变化，但是在指定的领域内可假定波动较为平稳。一般地，已知漂移的区域化变量P(x)，假设可分解为漂移和涨落两部分，如式(4)：

P(x)=m(x)+R(x)

(4)

式中，R(x)称为涨落。

那么区域化变量P(x)的分解可以这样理解：P(x)由两个不同尺度的现象合成；m(x)是在较大尺度下可以观察的现象变化；R(x)是在较小尺度下的现象变化，采取宏观和微观相结合的空间分析手段，适合复杂地质条件下空间变量的局部特征估计，这是泛克里金算法的突出优点，结合式(1)进一步变换可得：

E[(R(x)]=E[P(x)-m(x)]=0

(5)

据数理统计基础知识得知，涨落是一个数学期望恒定的区域变量，可认为涨落是围绕漂移m(x)摆动的随机误差，满足二阶平稳条件。经过文献查阅，易发现P(x)协方差函数与涨落R(x)的协方差函数相等，可参考文献[17]，此处不再赘述。

2 现场应用

2.1 确定涨落函数模型

小回沟煤矿已探明的82条地质构造中，46条断层走向长度不超过200m，根据常见的协方差理论函数模型并结合现场经验，选择球状模型进行拟合样本点估计量，进一步预测邻域内某点瓦斯含量值。在同一个单元内瓦斯含量是非平稳的区域化变量，存在线性漂移，其涨落满足二阶平稳，拟合的协方差函数为球状模型，如式(6)所示。

式中，d为样本点之间的距离。

随机取出5个样本点，将所有数据整理见表1，利用泛克里金法对表1中的0号点进行估计。

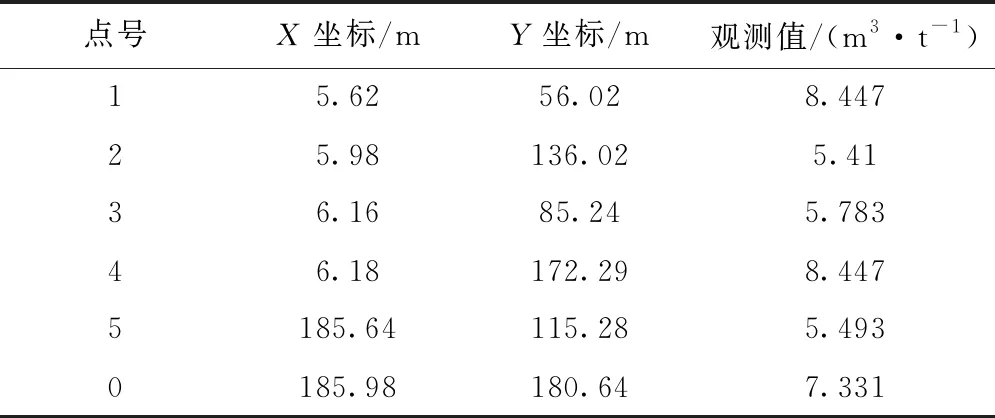
表1 观测数据

2.2 计算距离和协方差函数值

根据上述函数模型计算样本点之间的距离，并进一步计算出两点之间的协方差函数值，见表2。

2.3 计算结果分析

将表2数据整合后得泛克里金方程组权重矩阵，并将权重值代入泛克里金估计量公式(3)计算，第0号点估计值为7.57m3/t，实际测量值为7.41m3/t，误差为0.16m3/t。按照相同的流程选取小回沟煤矿2203工作面25个样本点分别进行计算，并与实测值进行对比，分析结果见表3，经验证，误差均不超过0.20m3/t，在实践中具有重要参考价值。

表2 两点之间的协方差函数值

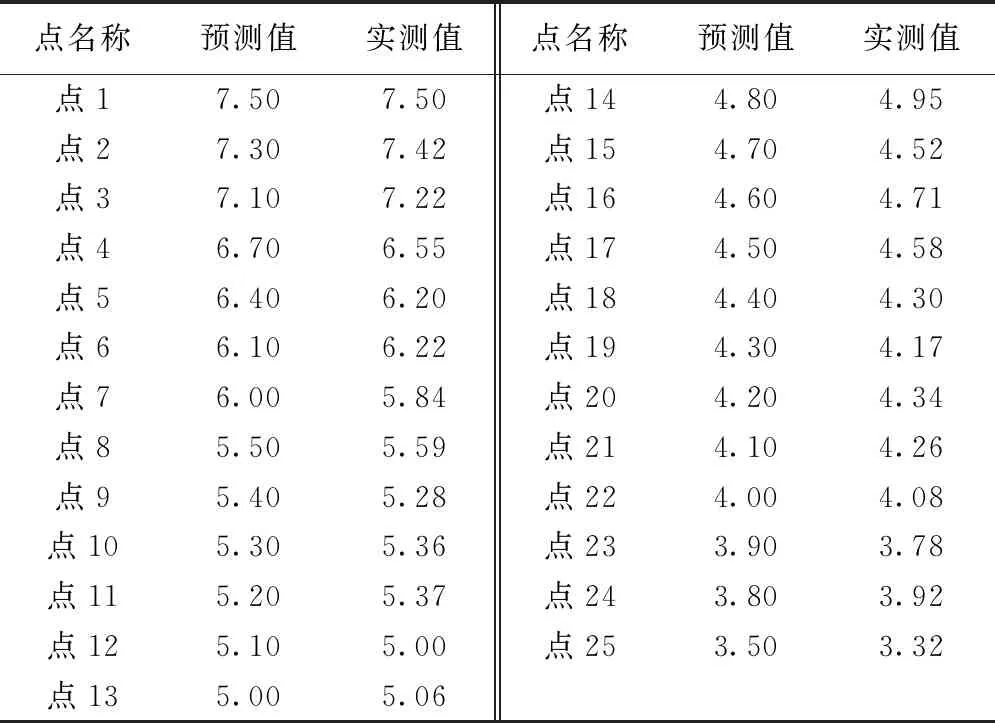
表3 样本点预测值与实测值 m3/t

3 软件系统研发

3.1 系统设计

瓦斯含量区域分级预测分布图是瓦斯地质图核心图件，随着瓦斯含量测点的不断变化需要动态更新瓦斯地质图，实现瓦斯地质精细化管理。矿井动态瓦斯地质图能集中反映煤层采掘揭露和地质勘探等手段测试的瓦斯地质信息，可较准确预测矿井未开拓开采区域的瓦斯压力、瓦斯含量、瓦斯涌出量等的区域分布。此外，反映矿井瓦斯赋存规律和涌出规律，分级分区域显现瓦斯灾害危险性程度。综上所述，动态瓦斯地质分析系统需要包含底图编辑，含量点、压力点、涌出量点绘制及等值线图与区域分布图绘制，系统模块构成如图1所示。

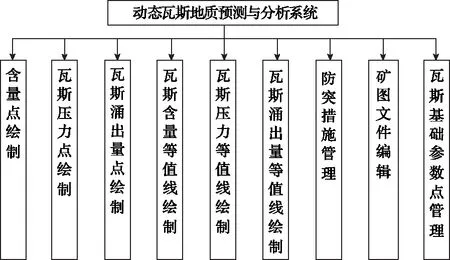
图1 瓦斯地质预测与分析模块

3.2 预测结果验证

3.2.1 区域预测图绘制

矿井瓦斯地质信息具有区域性、动态性、多维性等特征，因此需要进行地质单元划分，因小回沟矿瓦斯赋存主要受地质构造影响，根据地质构造分布初步确立地质单元边界，首先尽可能小范围确定地质构造影响空间，然后逐步加大影响半径，最后将各确定的较小范围地质单元组合，完成全矿井瓦斯地质单元划分。每个地质单元分别取样，对取样点进行过滤，筛选后的数据进行插值拟合形成数据集，并生成瓦斯含量等值线图和区域分级预测分布图。

将小回沟煤矿2203工作面瓦斯含量样本点数据导入所研发软件系统，生成瓦斯含量赋存状况区域预测图，如图2所示，取25个样本点进行实测后，应用所测数据对该算法分析模型准确性进行验证。其中，点1的大小为7.50m3/t，从左至右每条等值线的间距为0.10m3/t，依次减小，根据等值线标记的数值可推断矿井瓦斯含量的区域分布。

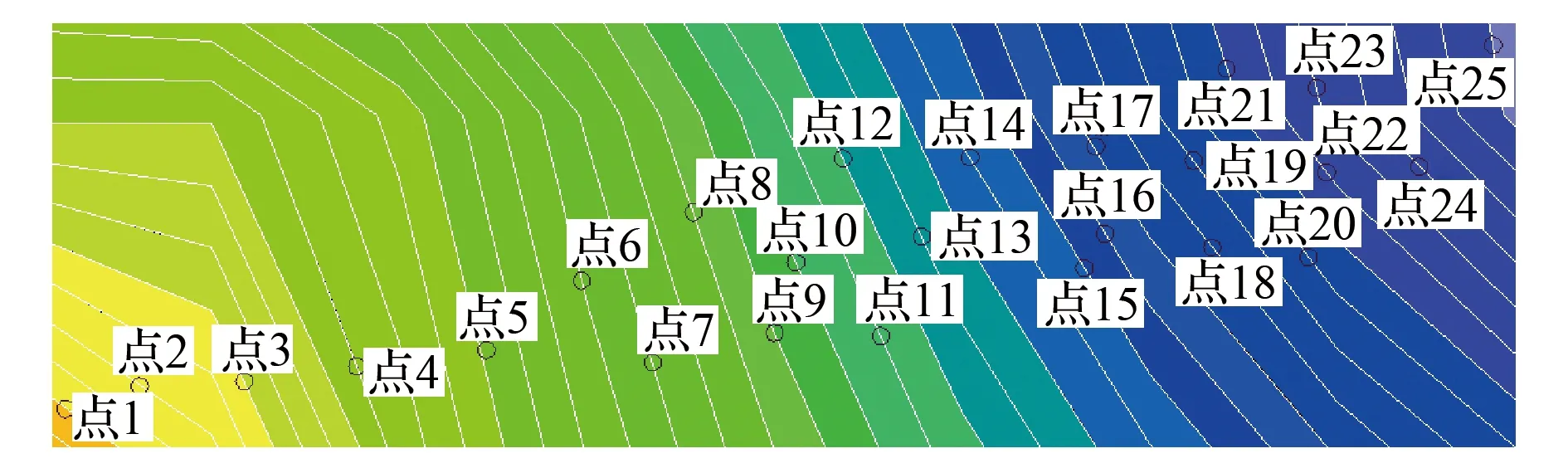
图2 验证点分布

3.2.2 误差分析

从图2中抽取25个验证点，分别命名为点1，点2，…，点25，根据预测图等值线的数值可推测出所有验证点的瓦斯含量预测值，然后根据样本点在矿井中所处位置进行瓦斯含量实测，将验证点预测值与实测值误差绝对值变化趋势绘制成曲线，如图3所示。由图3可知，抽取的样本点误差绝对值均位于0.00m3/t至0.20m3/t之间，当实测值大于7.00m3/t时，即该点处于危险区域内部，样本点均落在标注为7.00m3/t的等值线区域内部，根据矿井生产要求，立即启动红色预警，因此可认为误差为零，符合煤矿安全规范，预测精度处于行业领先。

图3 验证点误差曲线

4 结 论

1)根据瓦斯地质单元划分结果，采用泛克里金插值法进行瓦斯含量预测，准确率较高，既说明瓦斯赋存在空间上分布的复杂性，也证明复杂地质构造条件下的瓦斯含量具有可预测性。

2)采用泛克里金插值算法在同一地质单元内对瓦斯含量样本点进行插值过程中，地质单元划分的合理与否是决定预测精准性的前提，实际生产中，由于瓦斯地质状况的复杂性，随机变量漂移的不确定性都会影响预测结果。

3)动态瓦斯地质预测与分析系统，抽取空间样本点瓦斯含量数据，采用泛克里金插值算法可对矿井瓦斯含量进行智能计算与分析，自动绘制等值线和区域预测图，实现了瓦斯地质信息化与精细化管理。