基于双高斯纹理滤波模板和极值点韦伯对比度的圆柱锂电池凹坑缺陷检测

郭绍陶，苑玮琦

1 引言

由于生产工艺不当从而导致圆柱锂电池底部金属表面受到挤压而形成凹坑缺陷，其实际深度为0.1~0.5 mm，直径为1~3 mm. 凹坑形状多样、尺寸不一、深浅不同. 凹坑严重影响锂电池的使用性能和寿命，因此凹坑是圆柱锂电池缺陷检测的重要指标之一.

由于人工检测存在低效率、高误检率和高漏检率等问题，基于机器视觉的检测算法应运而生. 从目前掌握的文献来看，针对圆柱锂电池底部金属表面凹坑检测方法的研究很少. 朱慧［1］提出了基于3σ 准则和形态学提取电池端面凹坑的方法，该方法无法检测出视觉上不明显的浅凹坑，且没有排除噪声的干扰. 本文对基于机器视觉的金属表面凹坑检测相关研究进行文献检索发现，当前的算法虽然取得了较好的效果，但是并不完全适用于本文主要研究的浅凹坑缺陷，原因如下：

（1）目前的方法主要依赖图像的灰度值［2~4］，当采集到的图像背景亮度不均衡时，亮度变化小的凹坑会被背景淹没. 贺振东等［4］提出基于背景差分的钢轨表面缺陷检测算法，用图像每列的均值构成背景图像，与原始图像相减得到差分图像，采用自适应阈值分割法提取出缺陷，该方法的检测效果取决于所设定阈值的大小，过低的阈值会造成漏检，过高的阈值会产生大量噪声，对锈迹等抗干扰能力较弱；

（2）目前的方法很多依赖相邻像素的灰度差［5~8］，无法分割出亮度变化范围小，与背景的亮度对比度低的浅凹坑. 苑玮琦等［8］提出一种基于灰度差分模型的锂电池圆周面凹坑检测方法，该方法取得了较好的检测效果，但是由于本文金属表面的反射不均，使得该方法不能很好地检测本文的研究对象；

（3）目前的方法对弱信号的提取有效性不高［9~12］，不能同时检测深度不同的凹坑. 文献［9］建立了哈尔-威布尔方差模型，用局部斑块的哈尔特征代替局部梯度幅值特征，这种方法很难检测出渐变强度或低对比度的缺陷；

（4）近年来，基于深度学习的检测方法［13~15］取得了良好的效果，然而，因为在工业生产线上收集和标记大量的缺陷样品比较费时，并且相关方法高度依赖数据集，所以很少应用于实际检测中.

综上可知，目前关于圆柱锂电池底部凹坑检测的研究很少，本文提出一种基于双高斯纹理滤波模板和极值点韦伯对比度的检测算法，对于光照不均匀、金属表面反射不均及干扰纹理等情况具有较好的鲁棒性，有效提升了凹坑检测效果.

2 浅凹坑特征分析

浅凹坑凹陷程度非常小，轮廓模糊，人眼很难分辨，如图1（a）矩形框标注所示. 图1（b）为黑色虚线灰度分布曲线，可见，正常区域的亮度变化很小，相邻像素之间的灰度值有不同幅度的波动，浅凹坑与周围邻域的对比度低，灰度值呈先减小后增大的变化趋势，亮斑纹理灰度值比其邻域的灰度值略高，暗斑纹理灰度值比其邻域的灰度值略低，近乎相等. 整幅图像灰度分布不均匀，存在很多高频噪声，不能使用传统的缺陷检测方法检测凹坑.

综上可知，在一定的局部区域内，凹坑与背景具备一定的灰度差，因此，提出了一种基于底部金属表面反射特性的凹坑检测方法.

3 圆柱锂电池底部金属表面凹坑检测算法

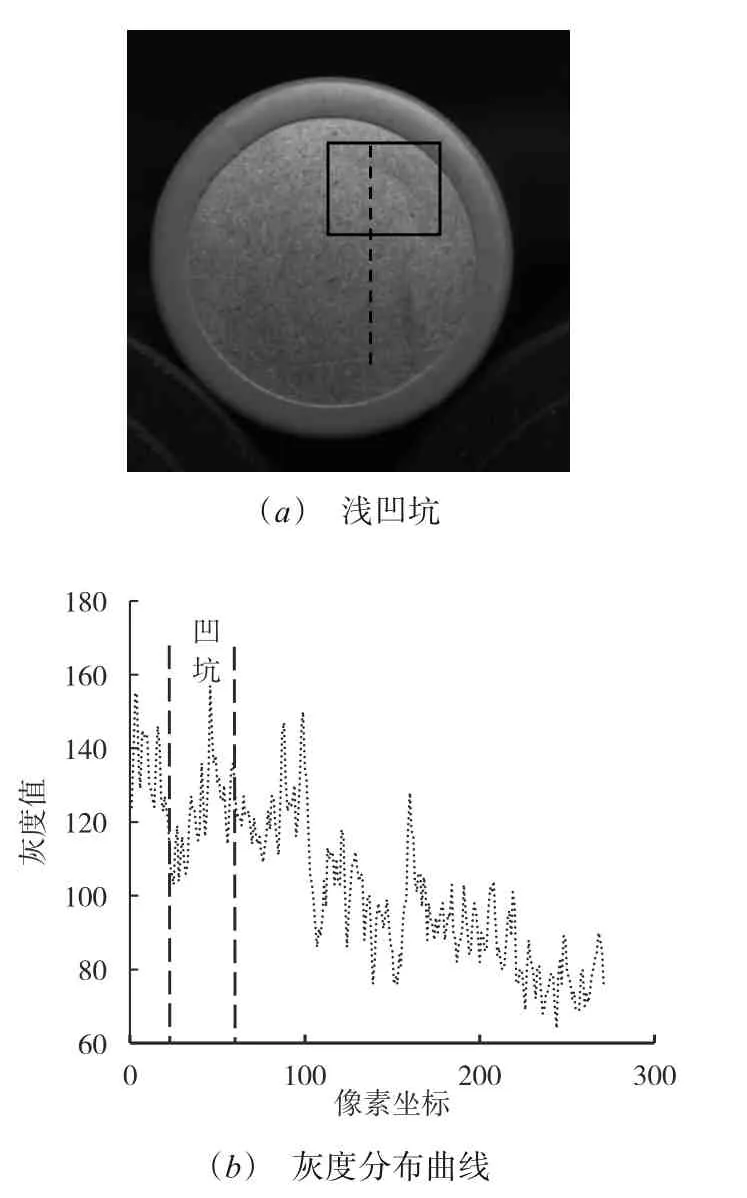
图1 浅凹坑及灰度分布曲线

利用近似于凹坑形状的双高斯纹理滤波模板与图像做卷积，在一定程度上削弱图像中不必要的高频信息，突出凹坑特征；找到卷积后所得的图像每列中具有最大韦伯对比度的像素点，确定凹坑候选区域；根据区域特征和灰度特征排除非凹坑纹理，完成检测，如图2所示.

图2 凹坑检测算法流程

3.1 图像预处理

利用Canny 边缘检测算子［16］、最小二乘圆拟合法［17］和Huber 函数［18］分割 出底 部金 属表 面图 像I（x，y）.

3.2 双高斯纹理滤波模板的定义和使用

从图1（b）可以看出，凹坑的灰度分布曲线有一个谷值和一个峰值，为了设计出可以满足不同形状和不同尺寸的凹坑的核函数，本文采用由反向的钟形高斯曲线和正向的钟形高斯曲线组合的方式，通过调节改进的高斯函数的参数，设计出具有凹坑纹理结构特征的滤波模板，将其与图像进行卷积运算，可以在抑制图像中不必要的纹理信息的同时，突出凹坑纹理. 本文设计的纹理滤波模板定义为由m×n个数排成的矩阵A：

其中，m和n的取值应该以能滤掉高频噪声且能保留凹坑内部对比度为原则.n的大小取决于凹坑的宽度，若n值过大，会导致浅凹坑被过度平滑，降低了局部对比度，所以，n需要等于图库中最小的凹坑宽度，取值为9.m的大小取决于图库中凹坑的最小高度，取值为14.

根据对凹坑纹理的结构分析，矩阵A中各分量值按照式（2）改进的双高斯函数等距采样生成.

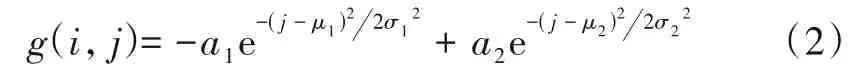
其中g（i，j）为当i∈［1，m］，j∈［1，n］时的函数值；a1和a2为正数，分别决定了曲线的谷值和峰值的幅度，通过统计图库中凹坑区域的灰度分布曲线中谷值和峰值的幅度比值发现，最小的比值为1.2，所以，a1取值为1，a2取值为1.2.σ1和σ2为高斯函数的标准差，随着σ1和σ2的增大，平滑效果越好，通过测试对噪声的平滑效果，最终选取σ1=1，σ2=4.μ1和μ2为高斯函数的两个均值，分别决定了曲线谷值和峰值的位置，本文根据凹坑暗斑和亮斑分别对应的灰度分布曲线长度的比值求得，μ1=2.5，μ2=9.5.

按照上述分析，构建的双高斯函数如图3所示.

将生成的双高斯纹理滤波模板Am×n与金属表面图像I（x，y）进行卷积运算，得到图像I′（x，y）.

3.3 极值点韦伯对比度的定义和使用

为了提高浅凹坑的检测率，本文引入人眼视觉感官特征，以韦伯定律［7］为基础，提出一种新的方法，称为极值点韦伯对比度（Extreme Point Weber Contrast，EPWC）.

（1）沿竖直方向提取灰度分布曲线，每条曲线之间间隔2个像素.

图3 双高斯函数示意图

（2）为了减少噪声点影响，用高斯函数平滑一维函数G（u，v），平滑参数取值为2.

（3）用函数G（u，v）表示每列的灰度分布曲线函数，（u，v）表示像素位置，其中v表示数据所处图像行，u为数据所处图像列，曲线上存在多个极值，而凹坑区域内的极大值和极小值的差值比较大，所以本文定义的极小值点（u，vc）处的极值点韦伯对比度EC（u，vc）如式（3）所示：

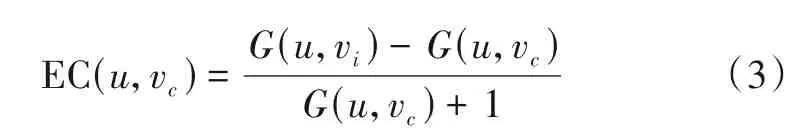
其中G（u，vi）代表在一条竖直灰度分布曲线上的某个极大值，G（u，vc）代表与G（u，vi）相邻的极小值，根据光源照射方向可知，i>c且EC（u，vc）>0.

根据上述分析可知，凹坑区域内EC 值应为最大值，计算每条灰度分布曲线上的极小值点处的韦伯对比度，得到最大的韦伯对比度ECmax（u，vc），将其与阈值T1进行比较，并求出该列的所有大于0的韦伯对比度均值M，将ECmax（u，vc）与M进行比较，这样可以减少噪声点造成的误检，如式（4）所示.

其中t为调整常数，T1和t的取值将通过实验获得，True表示像素点（u，vc）是凹坑区域的候选极小值点，False表示该条灰度分布曲线上没有凹坑候选像素点.

（4）根据上一步骤中求得的极小值点（u，vc），求出与其相邻的极大值点（u，vi），通过式（5）、式（6）得到凹坑候选像素在灰度分布曲线上的起始位置rs和终止位置re，则在此区间内的像素即为凹坑候选像素.

rs=vc（5）

re=vi+12 （6）

（5）对判断为有凹坑的曲线标记为1，根据凹坑宽度范围，定义若有大于3 条且小于106 条相邻曲线都被标记为1，则认为该区域为凹坑候选区域U.

3.4 排除非凹坑纹理

凹坑候选区域可能含有氧化锈斑、焊穿等非凹坑纹理，这些干扰纹理在竖直方向上会产生较大的EPWC，被误检为凹坑，排除非凹坑纹理步骤如下：

（1）将区域U映射回金属表面图像I（x，y）.

（2）根据先验知识，若区域U与图像中心点的最大距离小于42个像素，则为焊穿纹理；若区域U的高度大于91个像素或小于14个像素，则为非凹坑纹理；区域U中的最大灰度值小于92，则为非凹坑纹理.

（3）由于凹坑亮斑上下邻域存在一定的对比度，而非凹坑纹理的上下邻域的对比度较低，根据这个特征，将区域U映射回图像I′（x，y），提取区域垂直方向上中线的灰度分布曲线，计算两个连续的极小值点的极值点韦伯对比度EC（A），和极大值点与相邻的下一个极小值点的极值点韦伯对比度EC（C），根据式（7）判断区域U是否为真正的凹坑.

其中T2和T3是韦伯对比度阈值，将通过实验获得.

4 实验结果与分析

4.1 测试环境

测试本文算法实验的软件平台为Visual Studio C++2010，所使用的计算机处理器型号为Intel i7-4790，4 核，主频为3.60 GHz，内存为8 GB，操作系统为Win‑dows 7 64 位.

4.2 实验图库的建立

本文基于真实生产现场环境自行建立了一个18650圆柱锂电池底部金属表面图像数据库SUT-BYE，为了保证凹坑的完整度和清晰度，本系统对每个电池等角度60°拍摄6 张图片，每张图片分辨率为600×540.将SUT-BYE 分成两个子图库：凹坑图库SUT-BYE-B（209 个电池，共1254 张图片）和良品图库SUT-BYE-G（110个电池，共660张图片）.

4.3 算法评价指标

算法评价指标如下：

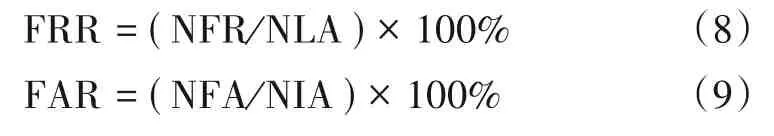
其中FRR 为拒真率，即有凹坑的锂电池被误检为良品的比率；FAR 为认假率，即良品锂电池被误检为有凹坑锂电池的比率；NFR 为有凹坑的锂电池被检测为良品锂电池的个数；NLA 为有凹坑的锂电池的总数；NFA 为良品锂电池被检测为有凹坑锂电池的个数；NIA为良品锂电池的总数. 对于图库SUT-BYE-B，同一个电池的6张图片中至少有一张检测为有凹坑视为一次检测成功；对于图库SUT-BYE-G，同一个电池的6 张图片中至少有一张检测为有凹坑视为一次误检.

4.4 算法关键参数的确定

4.4.1 阈值T1和调整系数t的确定

T1和t的大小将决定凹坑候选像素提取的准确性，对图库SUT-BYE-B 中的所有电池进行测试，如表1 所示，当T1=0.13，t=3.6 时，满足在不漏掉凹坑候选像素的情况下噪声最少.

表1T1和t不同取值时的FRR/%

4.4.2 阈值T2和T3的确定

T2和T3决定了排除非凹坑纹理的能力，在确定的阈值T1和调整系数t下，本文对图库SUT-BYE的所有电池进行测试，如表2所示.

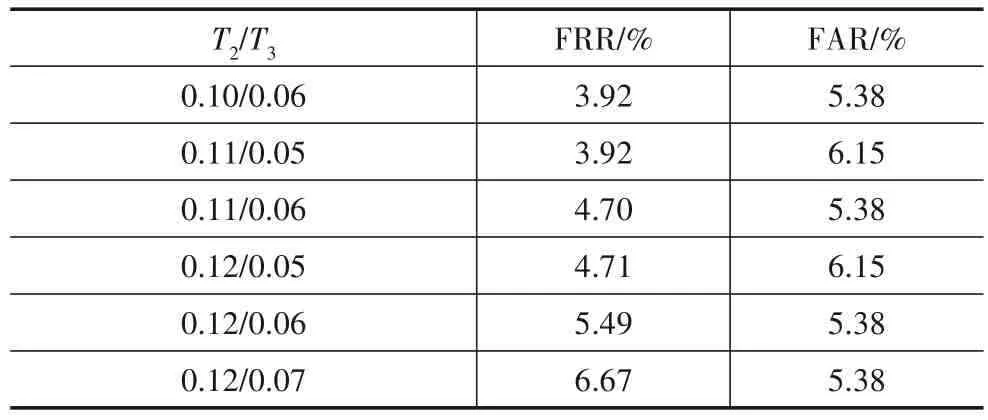
表2T2和T3不同取值时的FRR/%和FAR/%

可见，T2=0.12，T3=0.06 能保 证FRR 与FAR 的平衡，可获得最佳检测性能：拒真率是5.49%，认假率是5.38%.

4.5 与其他方法比较

将本文方法与其他表面凹坑检测方法进行了对比实验及分析. 实验过程中，所有参数的选择都是按照4.4节的方法获得的. 有凹坑的图像实验结果如图4所示，良品图像实验结果如图5 所示，从第一列到第六列依次为原始图像、金属表面图像、文献［4］方法分割效果图、文献［6］方法分割效果图、文献［7］方法分割效果图以及本文方法分割效果图. 表3 为FRR 和FAR 的对比结果.

实验结果表明，其他方法由于受限于局部特性和参数大小，没有充分考虑凹坑和非凹坑纹理的特征，导致检测效果不佳，本文方法定义了可以真实描述凹坑灰度突变特征的极值点韦伯对比度，并且通过定义的双高斯纹理滤波模板增强了凹坑灰度特征，能够消除光照不均和反射不均的影响，能排除一定的干扰纹理，所以能够比较完整地分割出不同深度不同尺寸的凹坑，得到了较好的检测结果.

图4 凹坑图像分割效果对比

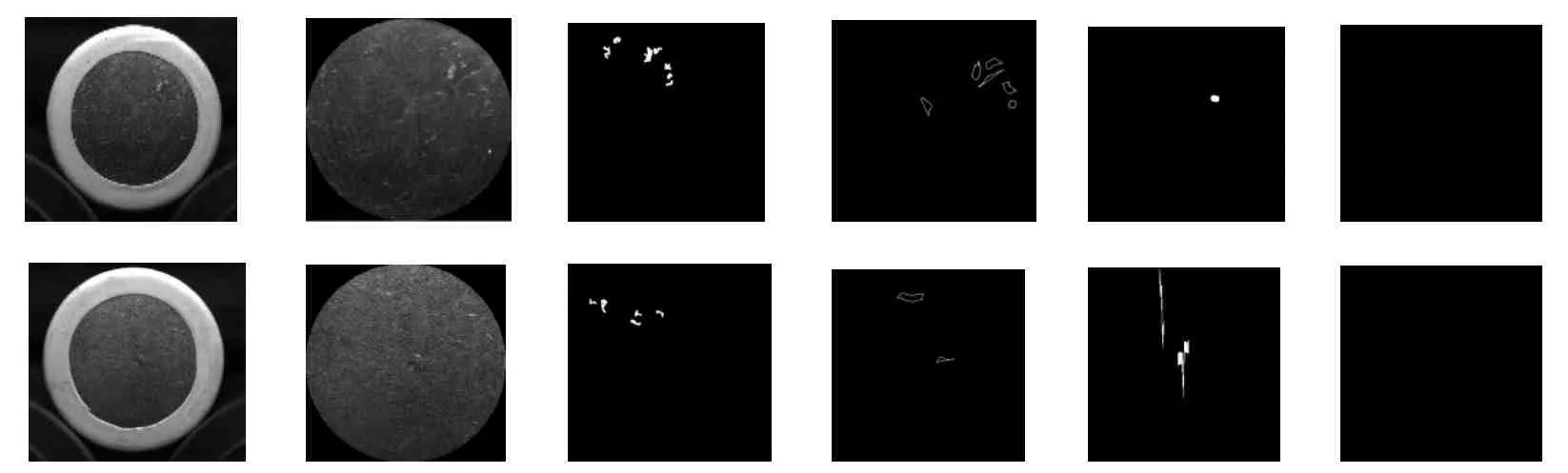
图5 良品图像分割效果对比

表3 算法性能指标对比

5 结论

本文在分析圆柱锂电池底部金属表面凹坑图像特征的基础上，提出了基于双高斯纹理滤波模板和极值点韦伯对比度的凹坑检测算法，在自建的图库上进行了验证，得出以下结论：

（1）本文方法不受锂电池壳体材料的限制，能够解决图像亮度不均、金属表面反射不均对检测的影响；

（2）定义的双高斯函数作为图像卷积核函数，计算简单，在对图像进行平滑降噪的同时保留了凹坑的灰度突变特征；

（3）本文将韦伯定律应用于图像特征引起的视觉刺激，根据金属表面反光特点，能够准确地提取出不同尺寸、不同深度的凹坑区域，并对噪声具有一定的抗干扰性；

（4）本文方法可以广泛应用于光照不均匀和反射不均匀的情况下，目标与背景灰度差异较小的微弱信号的检测问题，具有普适性和实际应用价值.