抗主瓣多假目标欺骗干扰EPC-MIMO波形自适应优化设计技术

张洋，位寅生，于雷

1 引言

为提高雷达对复杂环境的适应能力和满足雷达日益多样化的任务需求，20 世纪初国外学者将多输入多输出（Multiple-Input Multiple-Output，MIMO）技术从通信领域引入雷达领域，提出了MIMO雷达概念［1，2］. 相比于传统相控阵雷达，MIMO 雷达具备更优越的搜索、目标跟踪、抗饱和攻击性能等，可有效改善雷达战场工作能力［2］. 但随着现代电子干扰技术的不断进步，各种新型干扰不断被提出，特别是数字射频存储［3，4］（Digital Radio Frequency Memory，DRFM）欺骗干扰技术，一经提出便迅速被应用于各种作战场景. 如现代作战飞机、舰船以及低空突防目标等往往配备自卫干扰机，或与随队干扰机协同工作，在被雷达锁定后会通过DRFM 技术生成单个或多个主瓣假目标，诱使雷达锁定并跟踪假目标［5，6］，从而丢失真目标，严重影响了雷达系统的目标探测性能.

DRFM 欺骗干扰根据采样转发方式的不同可分为两种，一是全脉冲转发干扰［7］，干扰机对整个探测脉冲进行截获再转发；二是间歇采样转发干扰［8，9］，干扰机对探测信号部分片段采样后快速转发. 本文主要考虑全脉冲转发干扰的对抗. 对于全脉冲转发干扰，干扰信号相比于目标至少延迟一个脉冲宽度进入接收机，这导致假目标远远偏离真目标所处距离单元，极大弱化了干扰的欺骗性. 为此，干扰机一般通过调整干扰转发时延，延迟一个或多个脉冲重复周期（Pulse Repetition Interval，PRI），从而在目标所处距离-多普勒单元附近产生超前或滞后的假目标.

对于具有一个或多个PRI延迟的转发欺骗干扰，脉冲分集是解决该干扰的有效手段. 国内外已有学者开展关于脉冲分集抗干扰技术的研究，如设计具有低互相关特性或局部低互相关特性的波形组［10~13］使干扰信号与目标在快时间域失配，以及设计脉间相位编码波形使干扰信号与目标在慢时间域失配等［14~16］. 但这一类技术不适用于MIMO雷达体制，因此有学者提出了基于频率分集阵MIMO（Frequency Diverse Array MIMO，FDA-MIMO）雷达的欺骗干扰对抗方法. 该技术利用FDA-MIMO 波形的距离-角度耦合性，通过调整阵元间频偏量使干扰在发射频率域搬离雷达波束主瓣，成为旁瓣干扰，进而通过自适应波束形成在空域实现干扰抑制［17~22］，但自适应波束形成会带来计算量大，造成一定信噪比损失以及需进行干扰样本筛选［17］等问题. 为此，一种FDA-MIMO 雷达非自适应波束形成抗欺骗干扰方法被提出，其通过设计雷达阵元间的频偏量，使干扰在空域搬移至目标主瓣波束方向图零点，进而通过数字波束形成实现干扰抑制［23］. 但由于这种方法只能使干扰在发射频率域线性搬移，当主瓣内分布多个假目标情况下，难以将所有假目标都搬移至波束零点位置，假目标能量会通过旁瓣泄露到真目标检测区域，造成真目标检测失败.

针对主瓣多假目标欺骗干扰对抗的难题，本文提出一种基于阵元脉冲编码MIMO（Element-Pulse Cod‑ing MIMO，EPC-MIMO）波形自适应优化设计的干扰对抗方法. 阵元脉冲编码技术属于空时编码技术，空时编码技术最早应用于通信领域［24］，用于解决不同通道互干扰的问题，后引入雷达领域，具体包括快时间空间信道编码［25，26］以及阵元脉冲编码［27~29］等. 本文主要研究阵元脉冲编码技术，其是对积累周期内MIMO 雷达不同发射天线辐射的不同脉冲初始相位分别进行编码. 文中首先推导及分析了EPC-MIMO波形特性，建立了EPC-MIMO 雷达回波中的目标与干扰模型，证明了EPC-MIMO 波形抗欺骗干扰的内在潜力；进而提出一种基于EPC-MIMO 波形自适应优化设计的抗干扰方法. 该方法以真假目标空域相关性极小化为目标函数，建立了EPC-MIMO 波形自适应优化问题，分别考虑了真目标准确方位已知与未知两种情况，引入自适应梯度算法［30］进行优化求解，实现主瓣内多个假目标同时与真目标收发流型矢量准正交，其物理意义是使假目标能量分布于真目标检测区域外，因此在接收端通过数字波束形成即可实现干扰抑制，避免了文献［17~22］中自适应波束形成处理带来的问题以及解决了文献［23］中主瓣多假目标旁瓣能量泄露的问题；此外，考虑到所提EPC-MIMO波形自适应优化设计方法需要对干扰进行认知，同时考虑到战场环境的实时性要求，提出一种基于EPC-MIMO 波形的干扰快速认知方法，在较短时间内即可实现干扰认知，形成了波形设计-干扰认知闭环系统；最后通过仿真实验验证了本文所提抗干扰方法以及干扰快速认知方法的有效性.

2 EPC-MIMO雷达目标与干扰模型

2.1 EPC-MIMO波形定义

记雷达发射阵与接收阵分别是由M个与N个天线组成的等距线阵，阵元间距皆为d，此外，雷达收发共置，远场目标相对于发射阵与接收阵方位差异可忽略.记雷达第m个发射天线辐射的第l个脉冲信号为

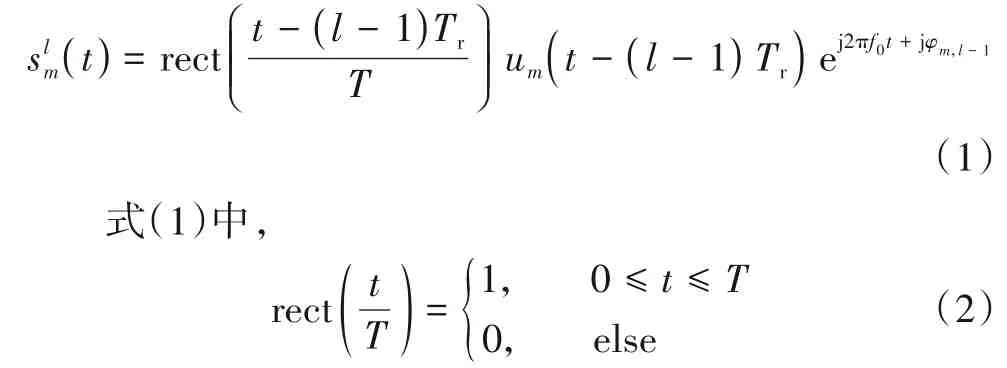
此外，式（1）中m∈｛1，…，M｝与l∈｛1，…，L｝分别为波形标号与脉冲标号，L为积累周期内雷达发射脉冲数，Tr为脉冲重复周期，T为脉冲宽度，f0为雷达工作频率，φm，l-1=(l- 1)φm为第m个发射天线辐射的第l个脉冲附加的相位，其中φm∈[0，2π]，um（t）为第m个发射天线辐射信号的基带调制信号. 为了描述方便，本文采用正交波形假设条件［31，32］，即满足下式条件：

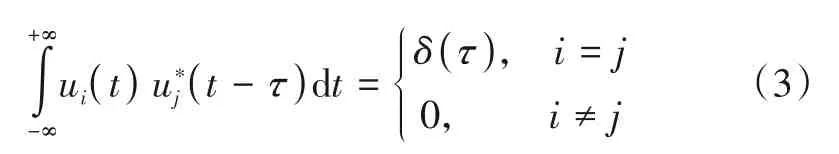
式（3）中i∈｛1，…，M｝与j∈｛1，…，M｝皆表示波形标号，（∙）*为共轭运算符，δ（τ）为冲激函数.

2.2 目标与干扰回波模型

假设存在一远场目标位于发射阵θT方位，接收阵θR方位，距发射阵与接收阵的径向距离分别为rT和rR，相对发射阵与接收阵的径向速度分别为vT和vR，由于雷达收发共置，可记θT=θR=θ，rT=rR=r，vT=vR=v. 则第n个接收天线接收到的第m个发射天线辐射的第l个脉冲信号回波可表示如下：

式（4）中ξ0为回波复系数，fR(θ) =dcos(θ) /λ为接收角 频率，fT(θ) =dcos(θ) /λ为发 射角 频率，由于fR(θ) =fT(θ)，下文中θ方位对应的发射角频率与接收角频率统一记为f(θ)，此外λ=为信号波长，τ=2(r-vt) /c为回波延时. 记雷达M个发射天线在第l个PRI 发射的信号为，其中（∙）T为转置运算符，则第n个接收天线单元接收到的回波信号为

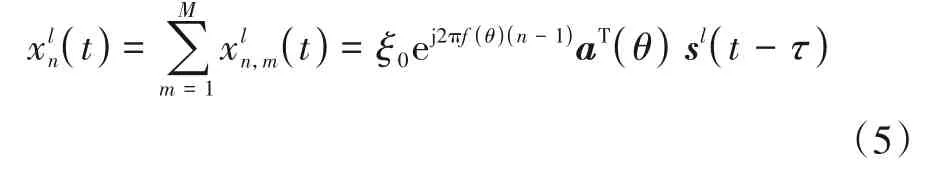
式（5）中a（θ）为对应θ方位的发射流型矢量，其可表示如下：

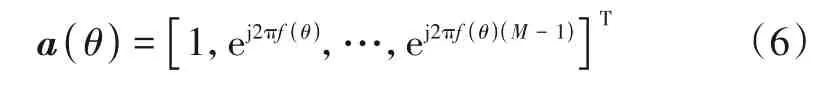
同理可将对应θ方位的接收流型矢量b（θ）表示如下：

进一步，对第n个接收天线单元接收到的回波信号进行多通道匹配处理［33］，来实现各天线单元发射信号的分离以及阵元脉冲码的解码. 记式（3）中回波延时pTr＜τ＜(p+ 1)Tr，且p=0，1，2，…，即雷达在第l个PRI发射的信号回波在第（l+p）个PRI进入接收机，因此用于多通道匹配处理的M个参考信号为[sl+p(t) exp{ - j2πf0t}]∗，其中第m个通道参考信号为首先对进而将其输入第m个通道匹配处理，输出结果去载频得到(τ)如下：

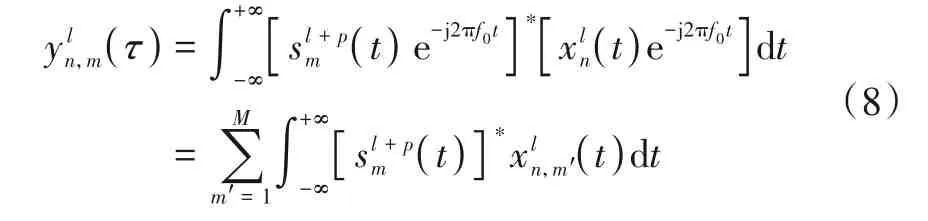
将式（4）带入式（8），同时由于不同发射天线辐射

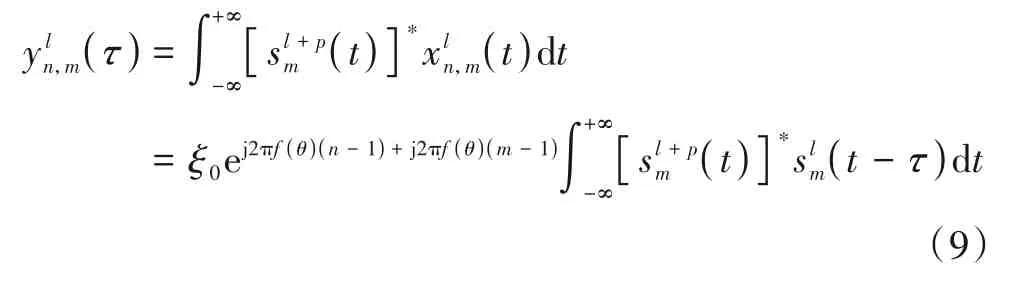
信号正交，因此式（8）可改写为进一步将式（1）带入式（9），可得

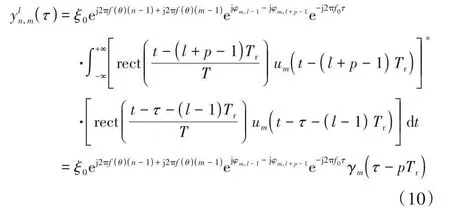
式（10）中γm(τ)为第m个天线辐射信号的自相关函数，由于不同天线辐射信号自相关函数差异较小，在此忽略，统一记为γ(τ)，则式（10）可进一步改写为

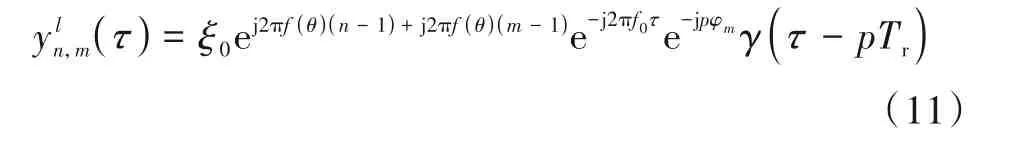
通过上述分析，对N个接收天线收到的回波信号分别进行多通道匹配处理，则NM个通道的处理输出结果yl(τ)可表示如下：

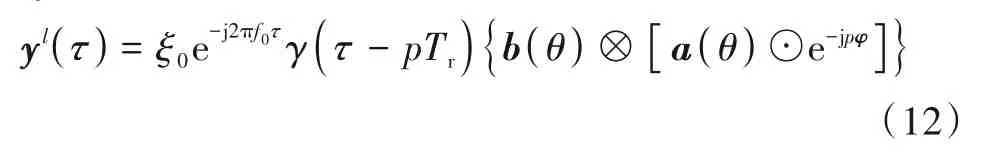
式（12）中⊗为Kronecker 积运算符，⊙为Hadamard积运算符，φ=[φ1，…，φM]T为可优化设计的阵元脉冲相位码组. 由式（12）可见，回波信号收发流型矢量可表示为

c(θ，p) =b(θ) ⊗[a(θ)⊙e-jpφ] （13）

式（13）中收发流型矢量除了与回波方位θ有关，还与阵元脉冲相位码组φ以及回波延迟脉冲数p有关，而回波延迟脉冲数p取决于回波延时τ，根据回波延时τ取值的不同，可分为以下两种情况：

情况①：当0 ＜τ＜Tr时，散射点回波无距离模糊，即回波在当前脉冲周期进入雷达接收机，p=0. 这种情况下回波空域收发流型矢量可表示为

c(θ，0) =b(θ) ⊗a(θ) （14）

情况②：当τ>Tr时，散射点回波距离模糊，即回波延迟一定PRI进入接收机，p=⎿（τ-τ0）/Tr」，其中⎿∙」为向下取整运算符，τ0为目标测量延时. 这种情况下回波空域收发流型矢量可表示为

c(θ，p) =b(θ) ⊗[a(θ)⊙e-jpφ] （15）

由上所述，根据回波延时是否超过一个PRI，可分为两种情况. 对于真实目标，其一般位于雷达最大无模糊距离范围内，属于情况①，记来自θs方位的目标回波收发流型矢量为cs（θs）：

cs(θs) =b(θs) ⊗a(θs) （16）

而对于延迟p个PRI，来自θI方位的假目标回波，对应的收发流型矢量为cI（θI，p）：

cI(θI，p) =b(θI) ⊗[a(θI)⊙e-jpφ] （17）

可见，EPC-MIMO 雷达回波中真目标发射角频率与接收角频率皆为f(θs)，位于发射-接收二维角频率谱对角线上［21］，而假目标发射与接收流型矢量分别为[a(θI)⊙exp(-jpφ)]与b(θI)，发射角频率不等于接收角频率，与阵元脉冲相位码组φ有关，因此可通过设计φ来使假目标能量分布于发射-接收角频率谱对角线外.图1 给出了θs=θI时，MIMO 信号与EPC-MIMO 雷达回波中真假目标回波在发射-接收二维角频率谱上能量分布对比图.

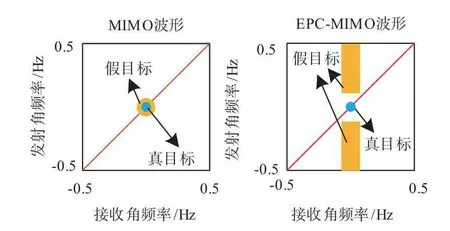
图1 真假目标发射接收二维角频率谱能量分布

3 EPC-MIMO波形自适应设计与干扰认知

3.1 EPC-MIMO波形设计方法

实际工作过程中，当目标被认定存在威胁时，雷达会打开跟踪文件，持续跟踪目标［34］，如火控雷达，具有自动跟踪能力，锁定目标后能不断准确给出目标坐标数据，转换成武器的射击单元，进而通过伺服系统实现火力武器的自动瞄准射击. 在这种情况下，位于远场的目标所处方位可看作已知，记为θs，功率为σ2s. 远场目标为摆脱雷达系统的锁定，会释放欺骗干扰来诱骗雷达系统使其脱靶，假设生成K个假目标，分别位于θI，1，…，θI，K方位，功率分别为，延迟脉冲数分别为p1，…，pK. 此外，回波中还存在白噪声，白噪声协方差矩阵记为RN=，其中为噪声功率，I为单位矩阵. 则雷达回波在目标方位做波束形成输出信干噪比SINR可表示如下：

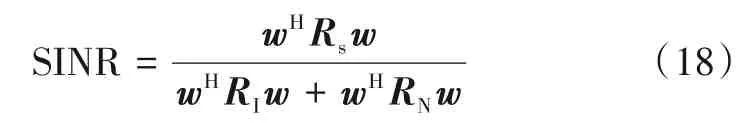
式（18）中波束形成处理加权值w=cs（θs）. 此外（∙）H为共轭转置运算符，Rs，RI分别为目标协方差矩阵与干扰协方差矩阵，由式（16）与式（17）可知，来自θs方位的目标回波收发流型矢量为cs（θs），延迟p个PRI，来自θI方位的假目标回波收发流型矢量为cI（θI，p），则目标协方差矩阵Rs与干扰协方差矩阵RI可表示为

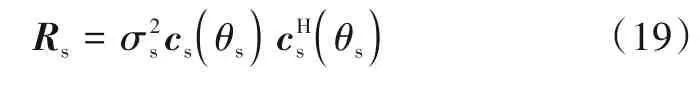
以及

结合式（19）与式（20），式（18）可改写为

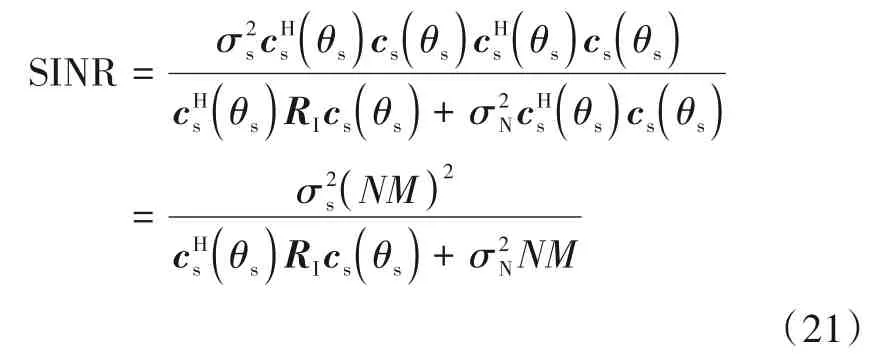
由式（21）可见，为获得最大输出信干噪比，可以通过极小化来实现. 其中干扰协方差矩阵RI由干扰方位、干扰功率、干扰延迟脉冲数以及阵元脉冲相位码组φ决定，前三个参量无法人为调整，因此可通过自适应设计φ来极小化极小化是为了使干扰与目标收发流型矢量准正交，其物理表现为使干扰能量分布于目标空域检测区域外.

由上所述，可将cHs(θs)RIcs(θs)作为代价函数，记为

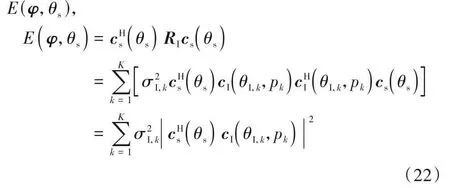
将式（16）与式（17）代入式（22），式（22）可进一步改写为

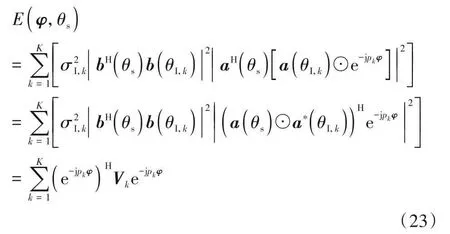
其中，

式（24）中|∙|2表示模平方.

当雷达锁定目标，目标准确方位已知时，为获得最大输出信干噪比，可通过极小化代价函数E(φ，θs)来优化阵元脉冲相位码组. 但实际作战场景中，由于测角精度，目标运动等因素导致雷达获取的目标方位信息不准确，目标位于角度区间κ=[θs-δ，θs+δ]内任意位置. 为此，可建立如下优化问题：

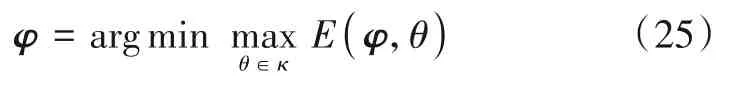
当式（25）中κ=θs时，表示目标准确方位已知的情况，可见目标准确方位已知情况下的优化问题为式（25）优化问题的一个特例.

式（25）最小最大优化问题为一多目标优化问题，但在单次优化中使最大值下降是一单目标非凸优化问题，在此采用自适应梯度优化算法［30］对其进行求解，如算法1所示：

算法1 自适应梯度优化算法

算法1 步骤3 中阵元脉冲相位码组φi对应调整量∆φi求解过程如下所示：

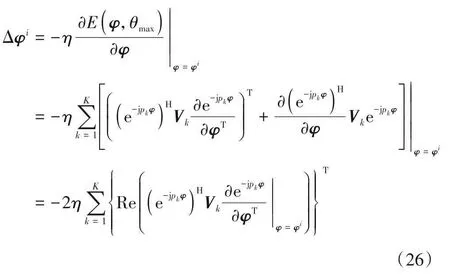
式（26）中η为步进因子，用于控制每次优化步长，其可自适应调整，调整方法参考文献［30］，在此不进行赘述. 此外，等式右侧中

其中diag（∙）为向量对角化运算符，将式（27）带入式（26）可得

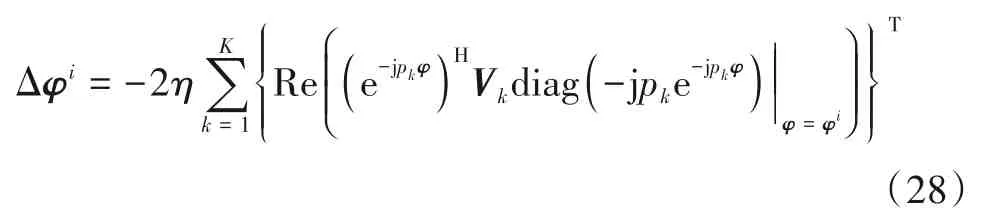
上文所述EPC-MIMO 波形自适应优化设计方法需要对干扰进行认知，为了形成波形设计-干扰认知闭环系统，下一小节给出基于EPC-MIMO 波形的干扰先验知识快速获取方法.

3.2 干扰参数快速认知方法

文献［6］提出了一种欺骗干扰认知方法，其以脉间随机相位编码信号作为试探信号，进而对积累周期内的回波进行多延迟相关通道处理，来提取干扰参数. 该方法需对一个积累周期内的回波接收结束后才能开始干扰参数提取，时间较长，难以满足战场实时性要求.此外，其无法提取干扰方位信息. 针对该问题，本部分对文献［6］所提方法进行改进，提出一种基于EPCMIMO波形的干扰参数快速认知方法，实现方法如下：

（1）雷达系统首先发射随机EPC-MIMO 信号作为试探信号，即φ=[φ1，…，φM]T中的M个相位值在0~2π范围内随机选取.

（2）选取某一天线接收到的回波进行多延迟相关通道处理，假设对第n个天线接收到的回波进行处理，记第n个接收天线单元积累周期内接收到的回波为dn（t），对其进行多延迟相关通道处理流程如下图所示：

图2 中每一个延迟相关处理通道都包括M个匹配处理通道，来实现不同发射天线发射信号回波的分离，不同延迟相关处理通道内用于多通道匹配处理的参考信号不同，下图以相关处理通道l的组成结构为例，具体给出了积累周期内不同脉冲重复周期用于多通道匹配处理的参考信号.

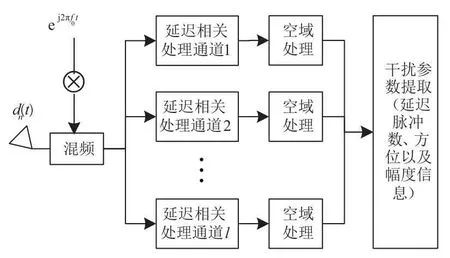
图2 多延迟相关通道处理方式

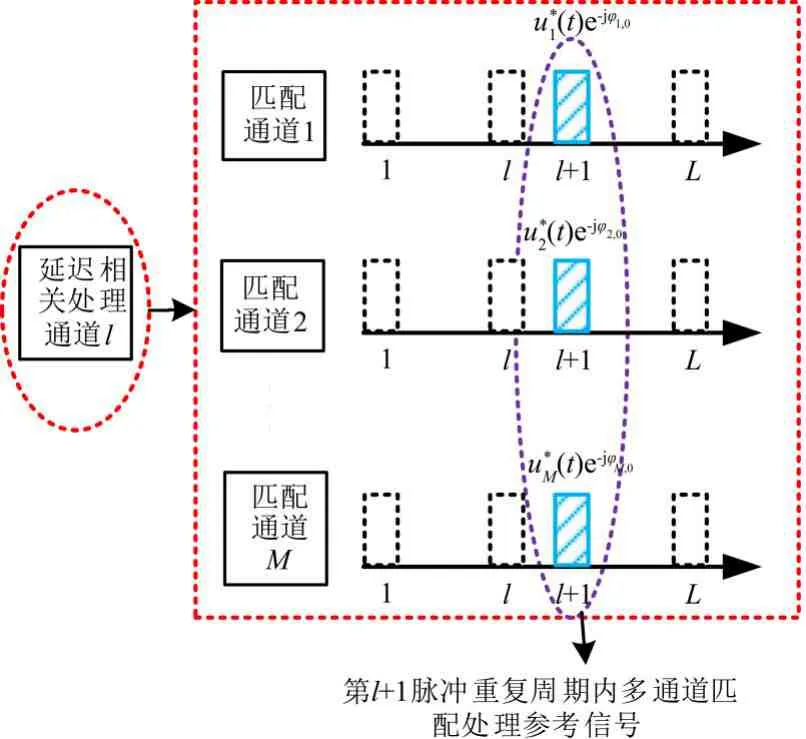
图3 延迟相关处理通道l组成结构

由图3可知，对于回波dn（t）中延迟l个PRI的干扰，将其在第l+1个PRI内的回波输入延迟通道l，与对应周期内的参考信号进行匹配处理可将附加的随机阵元脉冲相位码抵消，进而通过空域处理可输出峰值，而真目标回波以及延迟脉冲数不为l的干扰输入延迟通道l处理无法消除阵元脉冲相位码的影响，因此通过空域处理无法输出峰值. 基于这一原理可提取干扰延迟脉冲数以及方位信息.

（3）步骤2 获取了干扰延迟脉冲数以及方位信息，进一步可利用干扰方位信息，对与干扰延迟脉冲数对应延迟处理通道输出的结果进行滤波处理，提取干扰幅度信息.

由上述分析可知，当干扰延迟脉冲数最大为P时，在对前P+1 个脉冲周期内的回波处理后，继续对后续脉冲周期内的回波进行处理无法获取新的干扰信息.因此可设定当对连续Q个周期回波数据处理后都无法获取更多干扰信息，则停止处理，即对P+Q+1 个脉冲回波信号处理后即可实现对假目标先验知识的提取，相比于文献［6］所提方法需要对L个脉冲周期回波信号处理后才能实现干扰认知，更符合战场实时性要求.

需要注意的是，图2中的空域处理包括对延迟通道输出进行空域超分辨处理，来提取干扰方位信息，如MUISC 算法［35，36］，以及利用获取的干扰延迟脉冲数与方位信息进行空域滤波处理，来提取干扰幅度信息，如维纳滤波［37］，MVDR［38］算法等.MUISC 算法以及自适应空域滤波处理计算量主要受限于矩阵求逆过程，当匹配通道输出数M较小时，求逆计算量可忽略，当匹配通道输出数M较大时，可根据实际情况选取部分匹配通道输出进行处理，降低计算量.

由上所述，干扰认知方法需要对P+Q+1 个脉冲周期内的回波信号进行处理，每个脉冲周期内的回波需要经过多通道匹配处理来实现不同发射天线发射信号回波的分离，处理通道数为发射天线数M，即需要经过M次匹配处理，记一次匹配处理计算量为ς1，进一步需要对M个通道输出进行空域处理，记一次空域处理计算量为ς2，最后需利用空域处理获取的干扰方位信息对回波进行滤波处理，记一次滤波处理计算量为ς3，则总计算量可记为(P+Q+ 1)(Mς1+ς2+ς3).

结合本节所述干扰参数快速认知方法，可在发射自适应EPC-MIMO 波形用于目标探测的同时，对其回波进行多延迟相关通道处理，提取新的干扰信息，更新阵元脉冲相位码组，形成发射-接收闭环认知系统.

4 仿真实验

本节通过仿真实验对所提方法进行分析与验证，对比方法为正交MIMO 波形，FDA-MIMO 波形，随机EPC-MIMO 波形以及基于傅里叶基的EPC-MIMO 波形［28，29］，为便于后文描述，正交MIMO 波形记为MIMO波形，随机EPC-MIMO 波形记为REPC-MIMO 波形，基于傅里叶基的EPC-MIMO 波形记为FEPC-MIMO 波形，本文所提自适应优化设计得到的波形记为AEPC MIMO.

雷达阵元配置与波形仿真参数如表1所示：

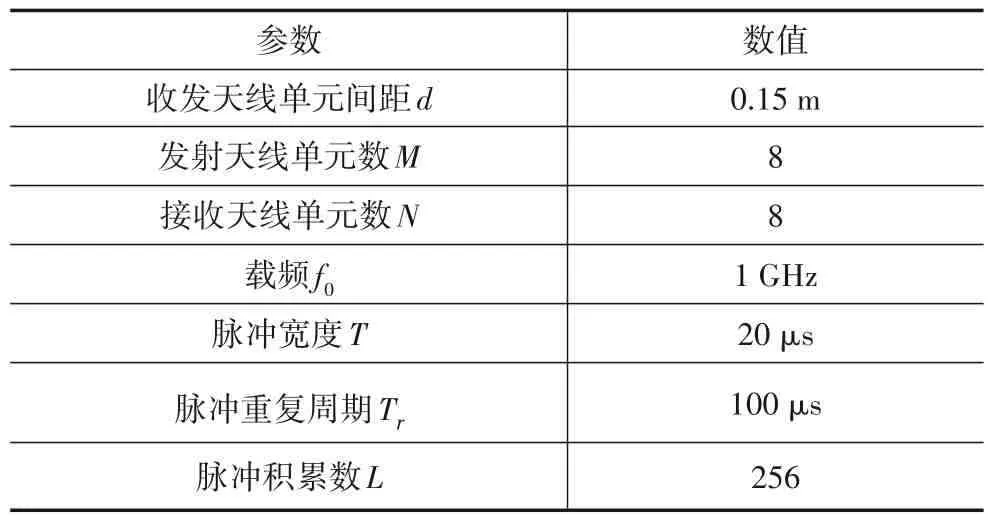
表1 雷达阵元配置与信号仿真参数

4.1 发射接收二维角频率谱分析

如2.2小节所述，本文所提波形可自适应调整干扰在发射频率域的能量分布，本节通过分析波形回波发射接收二维角频率谱来进行验证. 仿真场景中包含1个真目标与3 个假目标，真目标空域检测区域为87°~93°，真假目标仿真参数如表2所示.

图4给出了MIMO，FDA-MIMO，REPC-MIMO，FEPC-MIMO以及本文所提AEPC-MIMO 信号回波中真假目标发射接收二维角频率谱对比图，红色虚线框区域为真目标检测区域，其中FDA-MIMO 信号在回波中仅有一个假目标的情况下，可以通过调整阵元间的频偏，使得假目标搬移至真目标主瓣波束零点位置，但当存在多个假目标时，难以将所有假目标都搬移至真目标主瓣波束零点位置，为此本文仿真实验中FDA-MIMO 信号频偏量选取方式采用文献［39］所提方法，其可使回波中假目标都搬离真目标检测区域，并最大程度远离真目标所在位置，FEPC-MIMO 信号第m个天线发射的第l个脉冲附加的编码值为为回波中假目标最大延迟脉冲数. 由图4 可见，MIMO 信号回波中三个假目标都位于真目标主瓣区域，且假目标2方位与真目标重合；FDA-MIMO 信号回波中三个假目标在发射角频率维搬离真目标主瓣区域，但假目标部分能量依旧通过旁瓣泄漏到真目标检测区域；REPCMIMO 信号回波中三个假目标在发射角频率维噪声化，能量弥散在整个发射角频率维上；FEPC-MIMO 信号与FDA-MIMO 信号具有相同的能力，使干扰信号在发射维被搬移，同样存在假目标能量泄漏的问题；而本文提出的AEPC-MIMO 信号回波三个假目标能量在真目标检测区域形成了保护凹口. 通过上述分析可知，MIMO信号抗干扰性能最弱，FDA-MIMO 信号与FEPC-MIMO信号可使干扰在发射角频率维搬移，REPC-MIMO 信号可使干扰在发射角频率维白化，但由于这三种信号都存在假目标能量泄漏的问题，因此无法通过数字波束形成实现干扰抑制，而本文所提AEPC-MIMO 信号可使干扰能量分布于真目标检测区域外，因此通过数字波束形成即可有效抑制干扰，验证了本文方法的有效性.

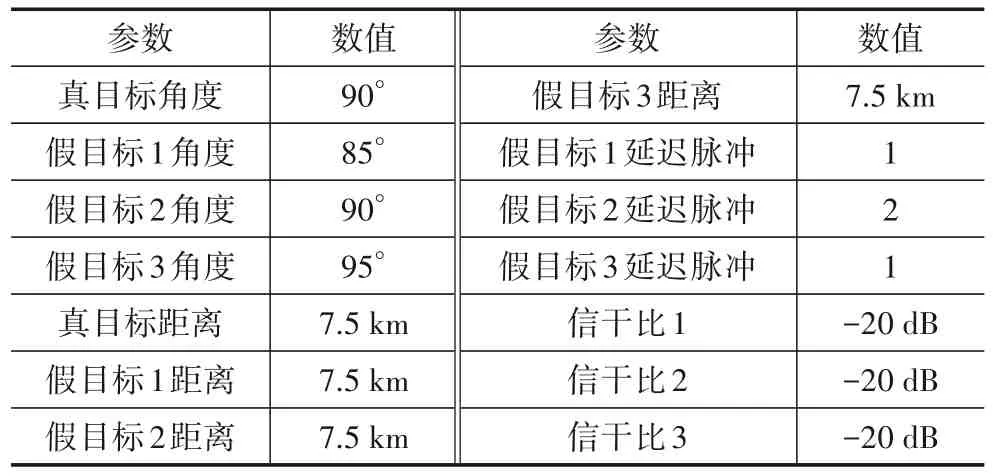
表2 真假目标仿真参数

4.2 波形抗干扰稳健性分析

本部分对所提方法抗干扰稳健性进行分析，由式（22）与式（24）可知，本文所提AEPC-MIMO 波形优化结果受目标检测角度区间κ，假目标数，假目标延迟脉冲数的影响，因此本部分设置三组子实验对这三个因素的影响进行分析.

4.2.1 目标检测区间κ取值大小影响分析

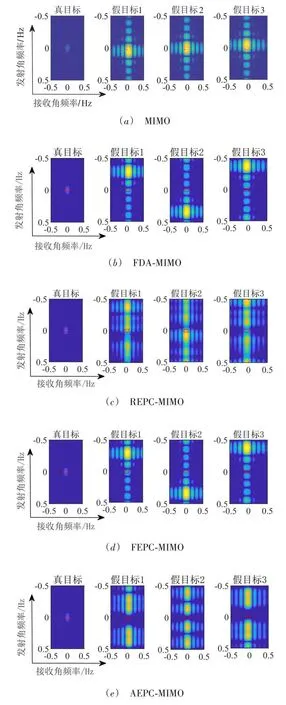
图4 真假目标回波发射接收二维角频率谱

该部分对目标空域检测区域［θs-δ，θs+δ］的大小对EPC-MIMO波形抗干扰性能的影响进行仿真分析，仿真场景如下：

假设存在3 个假目标，分别位于88°，90°以及92°方位，假目标延迟脉冲数皆为1，径向距离皆为7.5 km，输入信干比皆为-25 dB，真目标空域检测区域κ设置为［90°-δ，90°+δ］，图5 给出了随着δ值增大五种信号回波处理输出信干噪比的变化曲线. 其中MIMO 信号，FDA-MIMO 信号，REPC-MIMO 信号 和FEPC-MIMO 信号抗干扰性能与目标空域检测区域大小无关，MIMO 信号输出信干比约为-25 dB，FDAMIMO 信号与FEPC-MIMO 信号输出信干比约为0 dB，REPC-MIMO 信号输出信干比会波动，约为0 dB，可见这四种波形都无法有效抗干扰. 本文所提AEPCMIMO 波形输出信干噪比随着δ值增大而下降，当δ取值为5°时，输出信干噪比依旧可达16.61 dB，可见，在目标准确方位未知情况下本文方法依旧具备稳健的抗干扰性能.

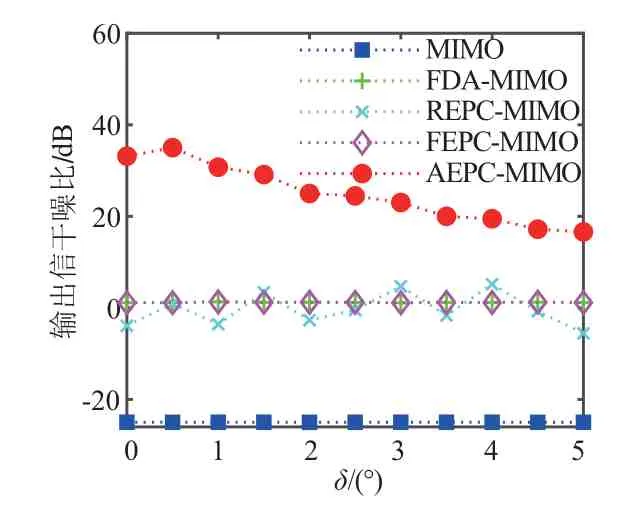
图5 目标检测区间κ对优化结果影响

4.2.2 干扰源数取值大小影响分析

该部分对干扰源数对EPC-MIMO 波形抗干扰性能的影响进行仿真分析，仿真场景如下：

假设存在一个真目标，位于90°方位，与雷达径向距离7.5 km，此外还存在P1 个假目标，均匀分布于（85°，95°）空间范围内，所有假目标延迟脉冲数皆为1，此外径向距离皆为7.5 km，输入信干比皆为-25 dB，图6 给出了随着P1 取值增大五种信号回波处理输出信干噪比的变化曲线. 其中MIMO 波形输出信干噪比约为-25 dB，未优化的REPC-MIMO 波形输出信干噪比在0 dB 附近波动，两者都无法有效抗干扰，FDA-MIMO 信号与FEPC-MIMO 信号在单假目标场景下输出信干噪比为33.58 dB，可有效抑制干扰，但在多假目标场景下会失效，而本文方法虽然输出信干噪比随着假目标数目增加而逐渐下降，但下降速度较为缓慢，在干扰数目为15 时，输出信干噪比依旧可达到31.67 dB，可见本文方法在多假目标场景下依旧具有较高稳健性.

图6 不同干扰源数情况下输出信干噪比

4.2.3 延迟脉冲数取值大小影响分析

该部分对干扰延迟脉冲数对EPC-MIMO 波形抗干扰性能的影响进行仿真分析，仿真场景如下：

假设存在一个真目标，位于90°方位，与雷达径向距离7.5 km，此外还存在P2 个假目标，均匀分布于（85°，95°）空间范围内，径向距离皆为7.5 km处，输入信干比皆为-25 dB，延迟脉冲数分别为［1，…，P2］，图7给出了随着P2取值增大五种信号回波处理输出信干噪比的变化曲线. 其中MIMO波形输出信干噪比约为-25 dB，未优化的REPC-MIMO 波形输出信干噪比在0 dB 附近波动，两者都无法有效抗干扰，FDA-MIMO 信号与FEPCMIMO 信号在单假目标场景下输出信干噪比为，可有效抑制干扰，但在具有不同延迟脉冲数的多假目标场景下会失效，而本文方法在P2 取值小于等于4 的情况下输出信干噪比可达33.53 dB，相比于前四种波形具有更稳健的抗干扰性能. 当P2取值大于4时，抗干扰性能下降，这是由于受限于波形优化自由度，可增加发射天线数改善.

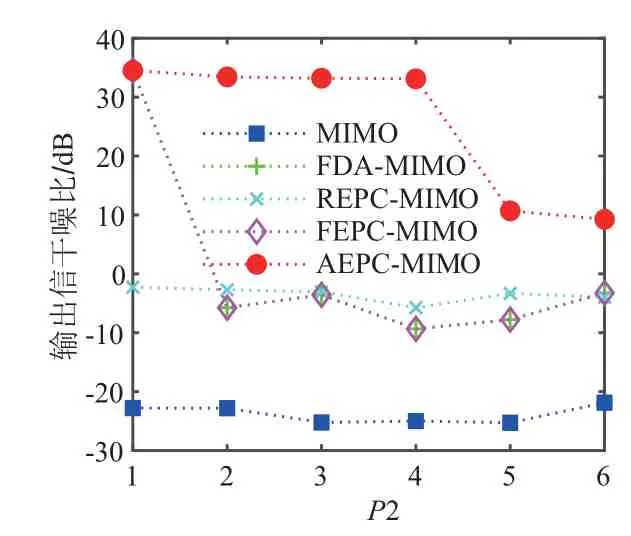
图7 不同干扰延迟脉冲数情况下输出信干噪比

4.3 干扰认知方法仿真分析

本部分对3.3 小节介绍的基于多延迟通道处理的干扰认知方法有效性进行验证，仿真场景中包含1个真目标与3个假目标，三个假目标信干比分别设置为-25 dB，-30 dB 以及-25 dB，径向距离分别为6 km，7.5 km，9 km，其他参数同表1与表2，用于多延迟通道处理的回波数据为第1 个接收天线在第4 个脉冲重复周期内接收到的回波信号，多延迟处理通道数设置为4，每个延迟通道处理输出分别采用MUSIC 算法处理，如图8所示.

图8 多延迟通道处理结果

由图8 可见，只有延迟通道1 与延迟通道2 存在峰值输出，峰值输出数分别为2与1，可见回波中存在2个延迟1 个PRI的干扰信号以及一个延迟2 个PRI的干扰信号，其中延迟通道1的两个峰值输出分别位于-0.043 Hz与0.043 Hz，分别对应85.0665°与94.9335°，延迟通道2的峰值输出位于0 Hz，对应90°，与设置参数相符. 为提取假目标幅度信息，进一步对延迟通道1处理输出结果分别在94.9335°与85.0665°方位进行自适应空域滤波处理，对延迟通道2 处理输出结果在90°方位进行自适应空域滤波处理，如图9所示.

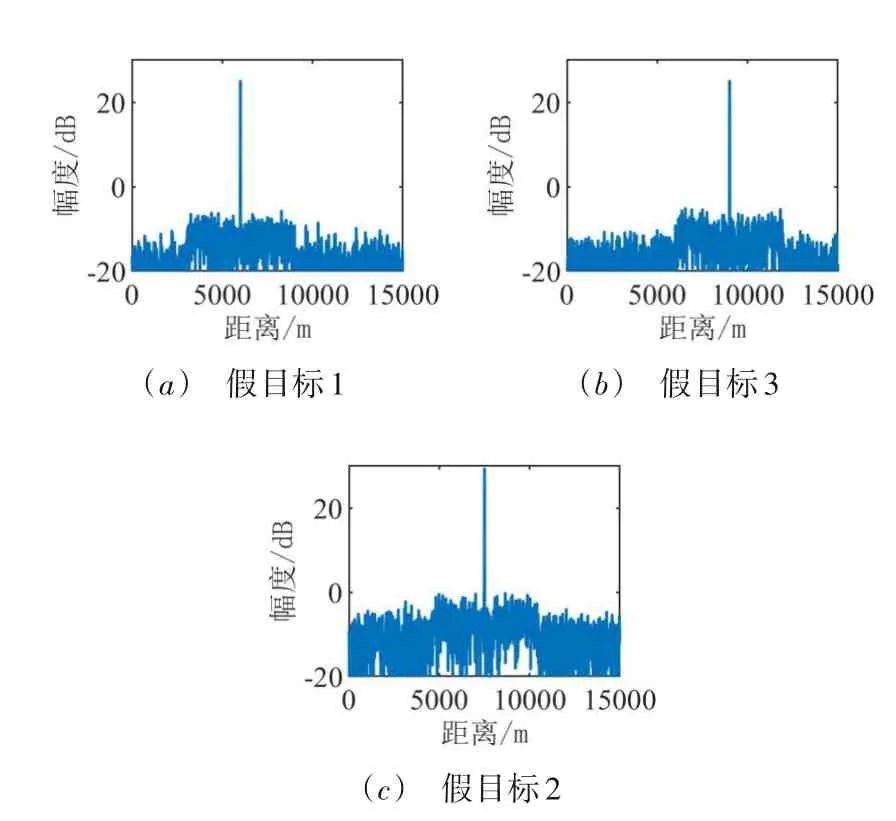
图9 自适应空域滤波处理结果

对不同假目标幅度进行相同的放大或缩小并不会影响式（24）所示优化问题优化出的最优相位码值，因此只需要提取不同假目标相对幅值信息即可. 由图9可见，假目标1 输出值为25.00 dB，假目标3 输出值为24.99 dB，假目标2 输出值为29.33 dB，假目标1 与假目标3 幅度相近，与假目标2 幅度相差约5 dB，三个假目标相对幅值差与设置值相符，可见3.2 小节所提方法可有效提取假目标参数.

5 结论

针对主瓣多假目标欺骗干扰抑制的难题，本文提出一种基于EPC-MIMO波形自适应优化设计的干扰对抗方法. 在对EPC-MIMO波形回波特性分析基础上，给出了基于认知的EPC-MIMO波形自适应设计方法以及干扰参数快速认知方法，形成波形发射-干扰认知闭环系统. 通过仿真实验，验证了自适应EPC-MIMO波形抗干扰有效性以及稳健性，以及干扰参数快速提取方法的有效性.