多通道盲电磁辐射现场分离方法研究
刘胜,王帮民,张兰勇
1 引言
由于船舶综合电力推进系统中,各类电气设备的广泛应用与密集放置,设备彼此之间存在各种耦合关系,不同设备的电磁辐射信号交织在一起. 并且各个设备的电磁特性以及传输特性事先无法得知. 因此,如何在没有设备电磁辐射信号先验知识的前提下,从复杂环境中获得各个设备自身的电磁辐射信号是进行系统级复杂电磁环境下设备电磁辐射测试所要重点解决的问题. 国军标中规定的设备电磁辐射测试的标准场地是电波暗室,但在该场地空间有限,仅能进行设备组装完成之前的电磁兼容预测试,难以满足系统级电磁兼容测试的需要,并且单台测试合格的设备在组装成系统时候仍然有可能出现不兼容的情况,因此有必要开展船舶综合电力推进系统多设备电磁辐射现场测试方法的研究.
现场测试的难点在于系统会受到环境噪声以及其它设备电磁干扰的影响. 常见的现场测试方法有虚拟暗室测试方法[1~5],基于波束形成的空域滤波方法[6,7]以及时频组合测试方法[8,9]等,但上述方法多是针对单台设备的现场测试,通过自适应滤波或者空域滤波等方法滤除设备电磁辐射信号中的背景噪声. 然而对于船舶综合电力推进系统而言,各设备之间分布密集,对设备电磁辐射干扰最大的往往不是环境噪声,而是其它设备的电磁辐射信号,这些信号往往处在相同的频段,常规的滤波方法难以奏效. 因此,系统级设备电磁辐射测试所要考虑的问题是如何在从现场测试采集到的电磁辐射混合信号中将多个电磁特性和传输特性未知的设备电磁辐射信号同步分离出来. 文献[10]已将盲源分离算法应用于同频基站杂波干扰抑制. 但船舶综合电力推进系统设备电磁辐射测试在应用盲源分离算法的时候有其独特的问题,即受限于船舶系统的空间有限和船舶正常运行的需求,不可能允许测试系统在设备周围放置过多的天线,这就要求提出的盲源分离算法能够在欠定条件下即测试天线数少于设备数的情况下完成多设备电磁辐射信号的分离. 常规的盲源分离算法如独立成分分析(Independent Component Analysis,ICA)对欠定问题难以取得较好的分离效果[11]. 解决此类欠定ICA 问题的一个重要思路是对输入信号进行预分解,构造虚拟通道,增加信号个数来解决欠定问题[12]. 比较常用的预分解手段是经验模态分解(Empirical Mode Decomposition,EMD),它可以将信号分解成多个本征模函数(Intrinsic Mode Functions,IMFs),实现简单且运行效率较高. 将EMD 与ICA 结合已广泛引用与脑电波信号伪迹去除[13,14]以及故障诊断[15,16],文献[13]利用集合经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)分解多元数据,之后利用熵和峭度筛选含有伪迹信号的IMFs,再利用ICA 得到多元数据中的伪迹,最后,ICA 和EEMD 的逆过程得到不含伪迹的多元数据,从而实现多元信号的伪迹去除. 上述算法虽在噪声抑制及故障诊断领域得到广泛应用,但较少涉及船舶多通道盲电磁辐射信号现场分离领域,究其原因还是因为EMD 是一种自适应的数据分析方法,它的分解结果取决于数据本身,在进行不同通道的EMD 分解时难免会存在不同通道分解IMFs 个数不一致的情况,从而导致同一阶次的IMFs 之间无相关信息,难以对分解结果进行横向考量. 文献[17,18]提出了一种多元经验模态分解(Multivariate Empirical Mode Decomposition,MEMD)通过改进EMD来保障不同通道信号的IMFs 分解个数一致,但其分解层数的不确定导致了筛选算法的设计困难. 另一个预分解手段是小波变换,通过设置小波基和分解层数来保障不同通道信号的分解层数和每层信号的频率域的一致性. 文献[19]将小波分解(WD,Wavelet Decompo‑sition)与ICA结合来解决脑电信号的伪迹去除问题. 但它的小波重构信号筛选方法,很难应用于船舶电磁辐射信号测试这样的高频领域.
因此,本文提出一种基于小波分解、相关性筛选以及独立成分分析的多通道盲电磁辐射现场同步分离方法(Wavelet Independent Component Analysis,WICA). 该方法利用小波分解构造虚拟通道解决欠定盲源分离问题,通过小波阈值去噪解决现场噪声问题,并设计基于信号相关性的筛选算法最大限度地保留有效分量,并最终实现大型系统多通道盲电磁辐射信号现场同步分离测试.
2 基于信号相关性的筛选准则的WICA算法
多通道盲电磁辐射现场分离问题的难点在于现场测试环境下噪声复杂,电磁辐射源之间耦合关系以及辐射特性未知,并且观测通道数受限于系统空间要少于电磁辐射源数.
针对上述问题,本文有针对性地提出了基于信号相关性筛选的WICA 算法. 该方法所要解决的问题如下:
(1)多通道信号去噪预处理问题;考虑到现场环境噪声复杂,WICA 算法采用小波阈值去噪对实际信号进行去噪处理,详见2.1节小波阈值去噪.
(2)有效分量的筛选问题;以信号相关性为性能指标,通过相关性的统计特征对有效成分进行筛选,详见2.2 基于信号相关性的筛选算法.
(3)多通道欠定盲源分离问题. 通过小波分解与ICA 结合,构造了虚拟的通道,解决多通道欠定盲源分离问题,详见2.3 WICA算法.
本文选用小波分解作为构造虚拟通道的手段,是基于如下的考虑:
(1)小波分解既可以保证分离结果的可控,又能通过调整小波分解的小波基和分解层数对分离结果进行调整,如增加分解层数使得分离结果在频率域上更加细化,调整小波基可以处理更多类型的信号.
(2)对每个信号采集通道进行相同的小波分解,可以保障每一个通道对应分解结果的次序和数目是一致的,每个通道的相同层数在频率域上对应相同的区间,这对于筛选算法的设计十分关键.
2.1 小波阈值去噪
考虑到实际信号往往受现场噪声干扰比较严重,在进行信号分离之前有必要对实际信号进行去噪处理. 而小波阈值去噪是一个很好的选择. 其核心在于阈值选取和阈值函数的选择. 为选取适合实测数据的小波阈值去噪参数,本文以均方误差(Mean Square Er‑ror,MSE)作为性能指标,比较不同分解层数level下,常用小波阈值去噪算法的性能,结果如图1 所示. 从图中可见,当阈值算法为‘visushrink’,阈值函数为‘less’时,MSE 最小,可保证性能指标最佳. 此外,该组合的小波阈值去噪性能受小波分解层数level的影响不大,因此,为降低运算复杂性,本文设置小波分解层数level=5. 综合使用经验,本文选择的阈值算法为‘visushrink’,阈值函数‘less’. 阈值算法‘visushrink’的阈值定义如下:
其中x是每层小波分解对应的小波系数,N表示每层小波系数的长度,T为每层选取的小波阈值.
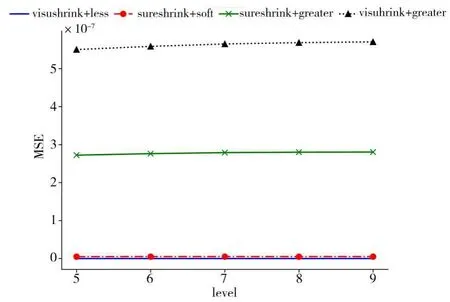
图1 不同level下,典型小波阈值去噪算法的性能
2.2 基于信号相关性的筛选算法
考虑到观测信号OBs(OBservation signals)经WD的虚拟通道扩展后分量成分复杂,由小波分解特性可知,在频率域上小波分解表现为将宽带信号划分为宽度不均匀的子带信号SD1,SD2,…,SDn,SAn,且所对应的频率是依次降低的. 如图2所示.
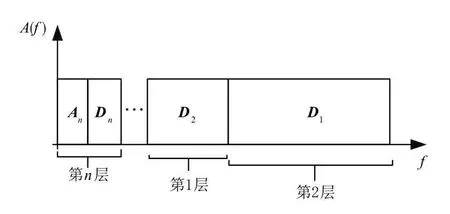
图2 频率域小波分解
WD 由分解和重构两个阶段组成:在分解阶段,产生一系列系数集,每个系数集表示信号在不同尺度上的信息. 如图3、4 所示,其中G1(z)表示高通滤波器,G0(z)表示低通滤波器,它们共同构成了分解滤波器组,↓2 表示降采样因子为2,↑2 表示升采样因子为2,H1(z)是合成高通滤波器,H0(z)是合成低通滤波器. 以3 层为例,原始信号S产生两组系数,即细节系数向量D1和近似系数向量A1. 这些向量是通过使用高通滤波器G1(z)进行卷积以获得细节分量,使用低通滤波器G0(z)获得近似分量,然后进行下采样来获得的.G1(z)和G0(z)构成分解滤波器组. 以相同的方式获得D2、D3和A3. 为了获得对应于A3的重构信号,首先,我们保留近似系数向量A3,剩余的系数向量设置为零. 其次,在Mallat算法的重构阶段重构上述系数向量. 我们可以用同样的方法得到D1、D2和D3的重构信号. 重构过程如图4 所示. 同样地,我们可以将3 层分解扩展到任意层数. 从整个分解过程可见,小波分解过程随着分解层数level 的增加,表现在频率域上就是不断的将近似分量即低频带进行平分,产生新的近似分量,而level层数的增加则对高频部分即细节分量不产生影响,因此在进行level 的选择时可根据实际研究频段进行选择. 以0~1 GHz 为例,分解层数level=5,那么D1~D5所涵盖的频率范围即为31.25 MHz~1 GHz. 如果需要更低频段的分解即可增加level 的层数,本文主要研究的频率范围30 MHz~1 GHz,因此选用level=5.
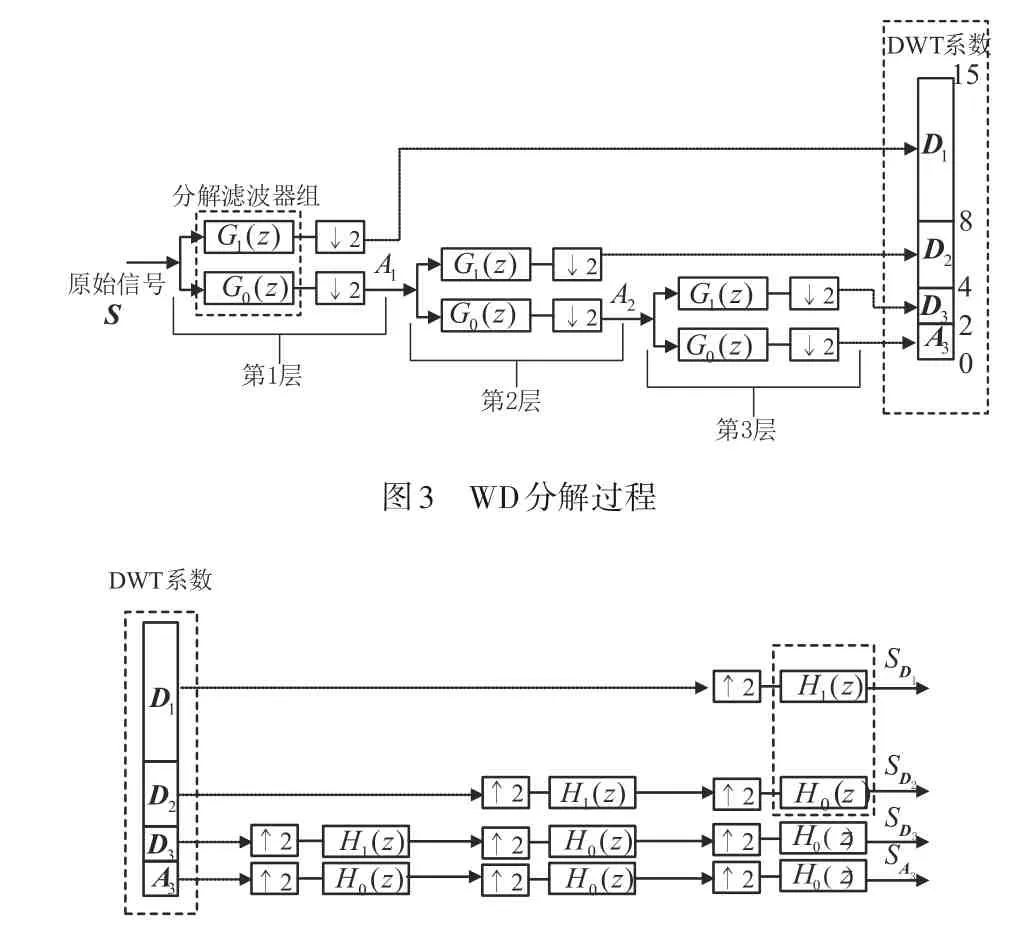
图4 WD重构过程
若直接将WD 结果应用ICA 获取独立成分(Inde‑pendent Components,ICs),ICA首先会对数据进行降维,其降维依据是计算输入信号的协方差矩阵特征值,之后对特征值进行排序,舍弃特征值较小分量. 这样做不仅会损失信号中能量不高的有效分量,而且可能会保留现场测试的低频成分,这是高频电磁辐射测试所不希望的. 因此有必要WD 信号预筛选,这样既降低了ICA 的计算负担,又最大限度地保留了目标信号中的有效分量. 此外,根据经验手动筛选不仅难以保证可靠性,而且也不满足现场测试快速性、实时性的要求.
为解决上述问题,本文提出基于信号相关性的筛选算法. 该算法的目标是从多通道的WD 信号中根据提出的算法自动确定的阈值筛选出包含要分离设备电磁辐射源信号的分量,为后续ICA 做准备. 该算法可根据信号相关性的统计特征自动调整阈值克服了经验筛选的弊端,且能够保证筛选序列与目标信号有较好的关联性.
基于信号相关性的筛选算法概述如下:在小波分解完成后计算WD 与OBs的相关性,根据相关性的统计分布特性确定相关性阈值,保留WD中相关性大于阈值的序列,并舍弃小于阈值的序列,最终将保留的序列组合成新的序列作为选中的分解序列,具体见算法1. 基于信号相关性的筛选算法的关键点有两个,一是WD和OBs 之间相关性的计算,见式(2);二是,筛选准则的确定,其中阈值threshold 取互相关系数(Cross Correlation Coefficient,CRC)四分位数.
阈值确定的关键指标互相关系数CRC定义如下:

其中,sd(n)和s(n)代表相关性比较的两个信号和分别是它们对应的信号均值.CRC 可以表达信号时
域波形形态之间的相似程度.筛选准则式(3)如下:

这里,comp_all 表示待筛选的信号序列,filter()代表筛选函数. 如果comp_all 的CRC ≥threshold 那么待筛选序列保留,否则舍弃.
值得注意的是,此筛选算法具有通用性,不仅适用于WD 的筛选,同样适用于其它信号分解算法比如EEMD. 基于信号相关性的筛选算法是本文提出WICA算法的核心,是区别其它分离算法,保障WICA 有效性的关键.
2.3 WICA算法
算法结构框图如图5所示,WICA算法分为三步:第1 步小波去噪分解并设置小波分解的小波基和分解层数n,将传感器采集到的N个通道的信号经过小波分解分解成N组长度相同的小波重构信号{Dij},其中,i=1,2,…,n;j=1,2,…,N;第2 步,基于信号相关性的筛选算法(见算法1),筛选出包含设备原始电磁辐射信号的分量,这一步既降低了后续FastICA 的计算量,又起到滤波效果,将包含噪声的分量剔除出去;实现与目标信号有关分量的保留和无关分量的剔除;第3 步,独立成分分析得到多设备电磁辐射目标信号ICs,将选中的小波重构信号整理成新的输入信号X,在进行FastICA之前先经过主成分分析(PCA)实现对原始数据的降维得到͂,再传入FastICA 分离出M个源信号Y. 值得一提的是相较于直接将第1 步分解的小波重构信号通过PCA 降维传入FastICA 进行分解,本文提出的WICA 增加第2步的意义在于,PCA 进行数据降维的依据在于计算输入信号的协方差矩阵特征值,之后对特征值进行排序,舍弃特征值较小分量. 这在复杂环境下的多通道盲电磁辐射信号中往往是行不通的,因为实际信号的小波重构分离结果中低频部分和高斯白噪声分量,往往会占据较大的特征值,不经过筛选而直接进行FastI‑CA 处理往往很难得到有效的分离结果. 本文提出WI‑CA 方法的第2 步是算法的核心,它综合考量了小波分解特性和重构信号的相关性,保证了后续FastICA 分离效果的有效性.

图5 为基于相关性筛选的WICA 算法流程图,其具体实现见算法2.
3 试验验证
为验证提出的WICA 算法在解决多通道欠定盲电磁辐射现场分离问题的有效性,本文采用某游轮发电机组现场电磁辐射测试数据作为验证数据.
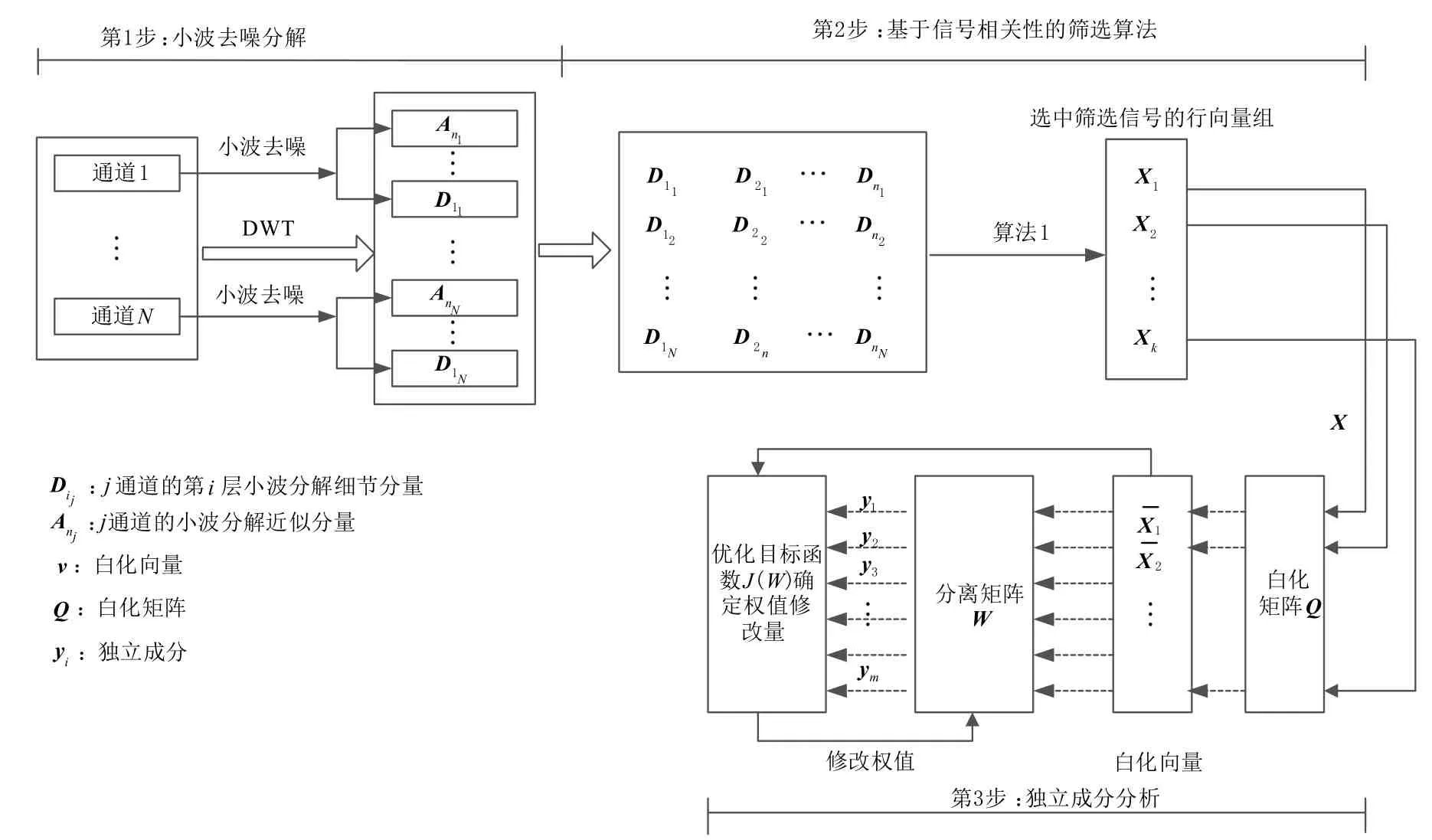
图5 基于相关性筛选的WICA算法结构框图

测试条件:在游轮额定工况正常运行下展开测试,测试系统及天线模块现场布局如图6所示,三组天线模块之间的间隔设置为2.5 m,天线高度设置为1.5 m,天线模块分布在一条直线上.
测试系统采样参数设置:采样频率fs=2 GSa/s,存储深度N=4 M,采样时间
此外,引入EEMD-ICA 作为对比算法,使用相关系数CRC 和信号相关性Cxy(式(4))作为性能指标,验证算法的有效性.
信号相干性Cxy定义如下:


图6 额定工况下测试系统及天线模块
其中,Pxy是信号x(n)和y(n)的互谱密度,Cxy用来表征两个信号频域的相似性.
图7 显示了利用天线1、2、3 获取的EMR(Electro Maganetic Radiation)信号的幅值频谱和通道间的相干性. 通过比较3个天线获得的EMR信号,可以确定发电机在额定状态下产生的EMR 信号覆盖的频率范围很广,各天线获得的EMR 信号相差很大. 从通道之间的相干性可以看出,各通道信号之间的共同分量大致了解,相干性在0.8 以上的频率点收集在图8 中. 这个结果是由四个发生器的EMR 信号之间的耦合引起的. 然后用所提出的MEMD-ICA算法将每个发生器的EMR信号从上述三个天线(通道)收集的混合EMR信号中分离出来.
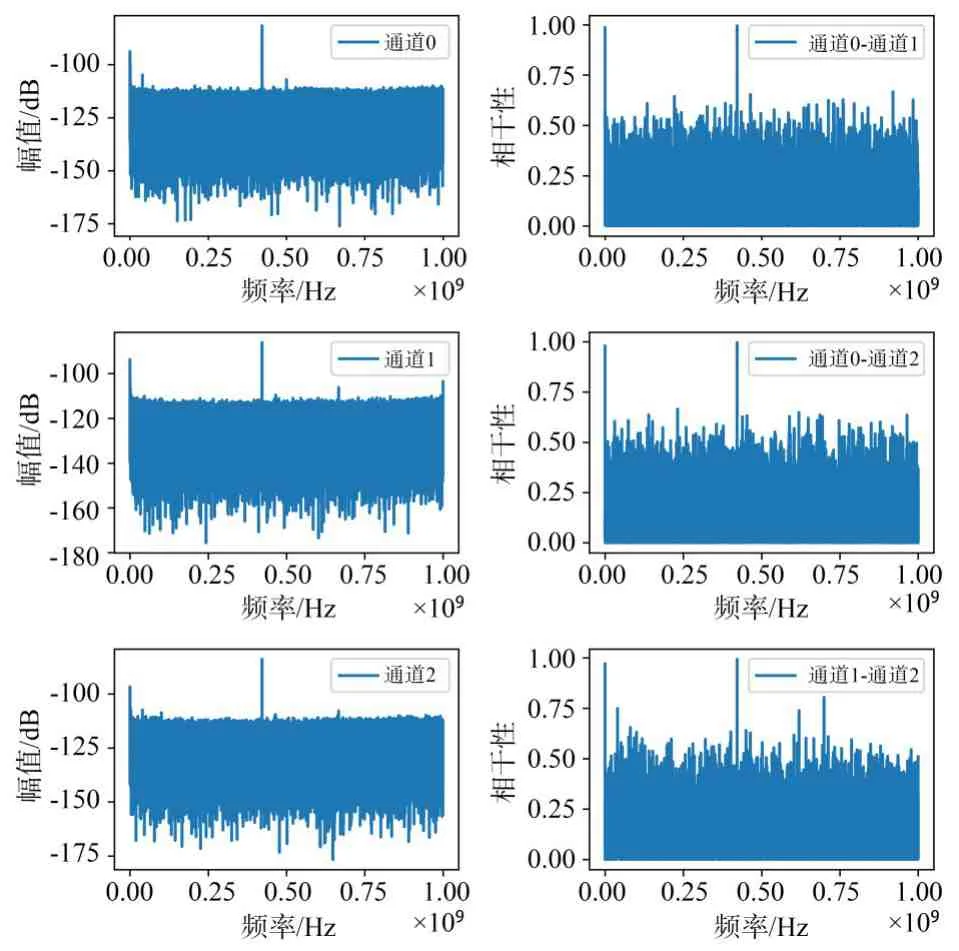
图7 各通道EMR信号的幅值谱与相关性
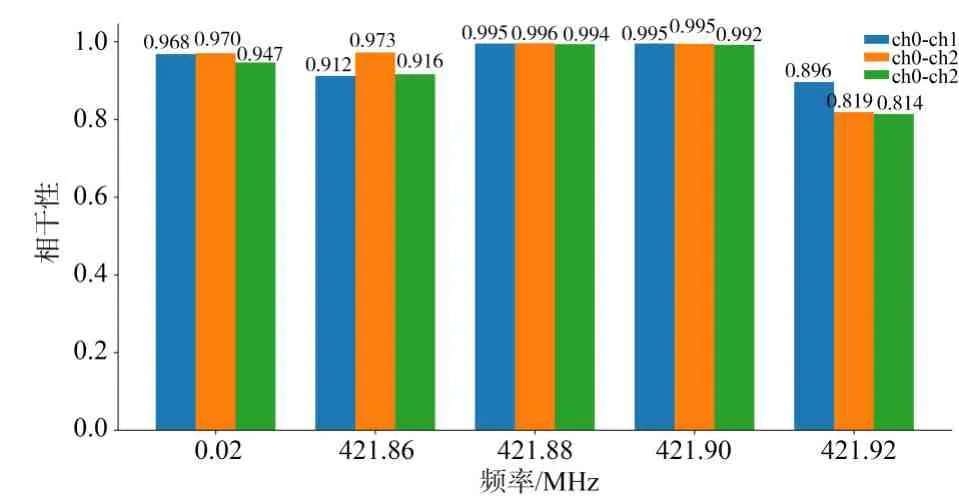
图8 两通道间相关性大于0.8的频点的分布
在获取现场电磁辐射数据后,使用WICA(算法2)和EEMD-ICA 算法首先分别对数据执行WD 和EEMD操作,使用算法详细参数见表1,结果如图9所示. 由图可见,WICA 可以保障三个通道信号分解层数相同(6层),且每层所对应的频段一致. 而EEMD 分解层数并不一致(通道0分解8层,通道1和2分解为7层),因此,通道对应IMFs 之间没有明确的对应关系,这将不利于信号的筛选.
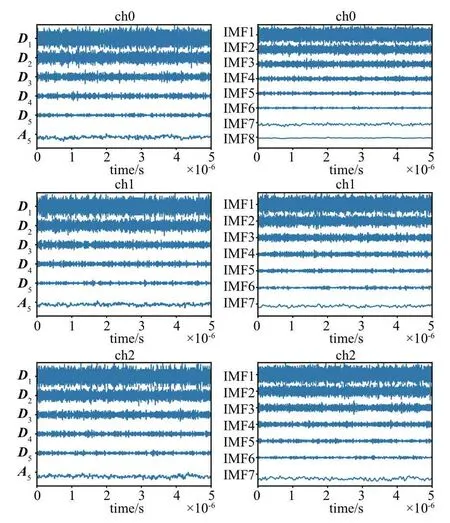
图9 WD与EEMD分解结果
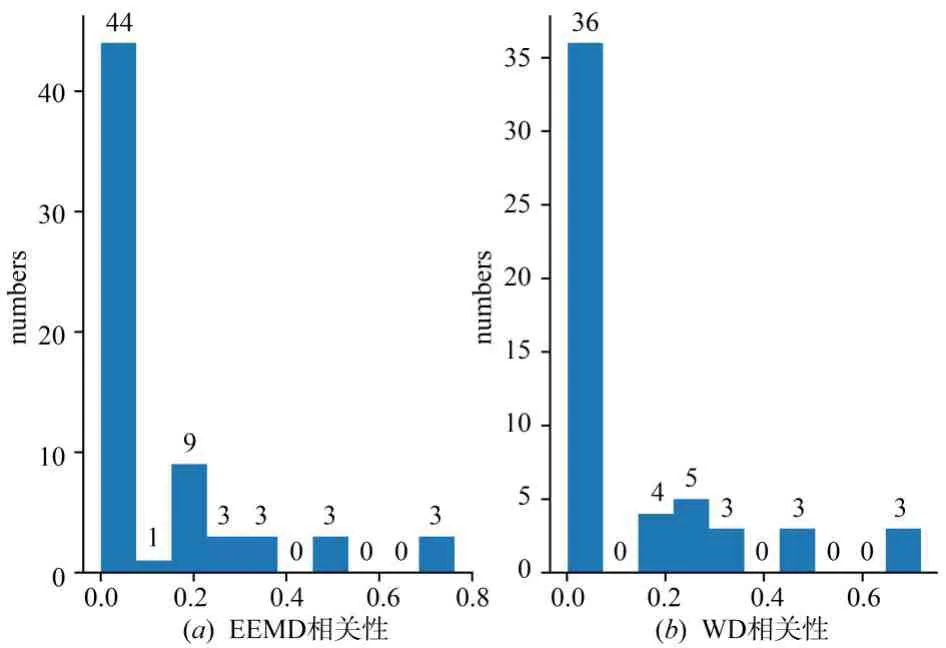
图10 不同算法下三通道分解结果与观测通道相关性分布
之后,将本文提出的基于相关性的筛选算法分别应用于EEMD 和WICA 以获取筛选分量. 图10 和11 分别给出了EEMD/WD 分解结果与观测通道相关性的分布直方图和箱线图. 图11 可见,WD 和EEMD 的相关性分布类似,但WD 分量所对应的相关系数分布更为紧凑,且WD 的中分位和四分之三分位都要高于EEMD 的分解结果,这说明WD 中的有效分量更加集中,筛选结果可以更加有效的剔除无关分量,并保存有用分量. 根据算法1确定的相关性阈值(EEMD 0.47/WD 0.49)也验证了这一点,说明筛选算法对WD 的筛选效果更佳. 此外,算法1 还给出了EEMD 和WD 的筛选结果如表1 所示,从表中可以看出,被舍弃的分量大多是分解结果里的低频分量,这符合相关分量信号筛选的直观印象. 但对具体算法而言,仍有较大的不同,EEMD-ICA 对于各通道的高频分量IMF1和IMF2都予以保留,而WICA在ch2通道中将D2分量剔除,也说明了筛选算法对WD的筛选更为精细. 之后将上述选择的分量selected_comp组成新的数组,送入ICA,进行后续处理,两种算法的频域的分离结果如图12 所示,左图为EEMD-ICA 分解的ICs,右图为WICA 分解的ICs. 其中分离结果ICs 即为测试对象4 组发电机组的辐射源,WICA 的分离结果中不仅分离出了观测信号中包含的20 kHz,421 MHz,而且还包括观测信号中淹没的520 MHz. 这说明了WICA 的分离结果即为每个发电机组的辐射源的信号,它们之间一一对应,并且具有唯一性. 此外,从图中可见EEMDICA 和所提出的WICA 都做到了从3个设备电磁混合信号(OBs)中分离出了4个ICs,证明了扩展虚拟通道解决欠定盲源分离问题的可行性. 但从两种算法ICs频谱的对比定性表明WICA分离的ICs保留了更多的频率成分如IC1 的200 KHz,600 MHz 等,而这 些频 率成 分在EEMD-ICA 的ICs 中完全丢失,这也证明了EEMD 在有效分量的聚合方面不如WD. 此外,WICA 的ICs 从频谱上区分明显,不同ICs 有较大的差距,而EEMD-ICA 的IC0,IC2,IC3的频谱区别并不大.

表1 EEMD‑ICA与WICA采用基于相关性的筛选算法比较
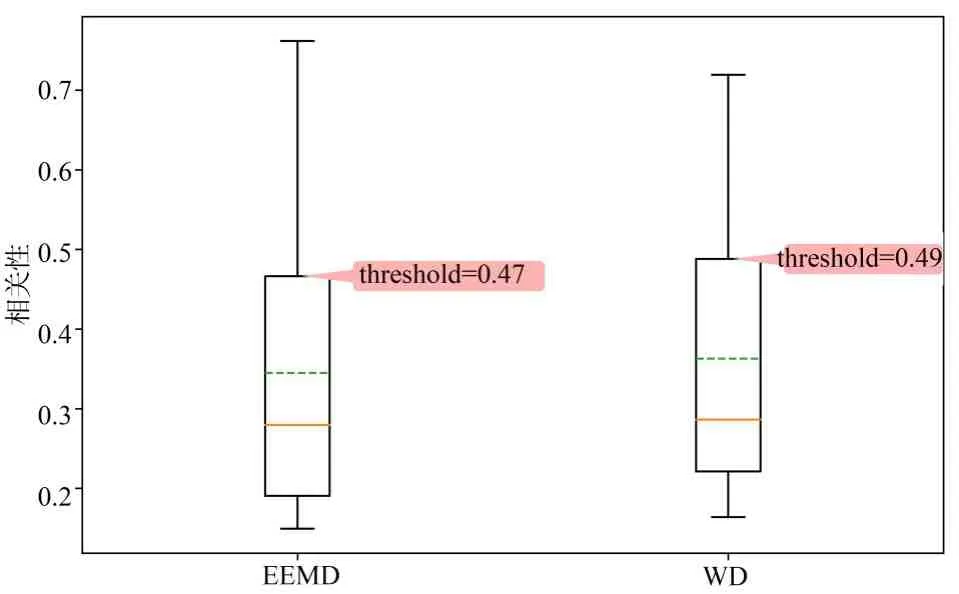
图11 不同算法下CRC分布箱线图
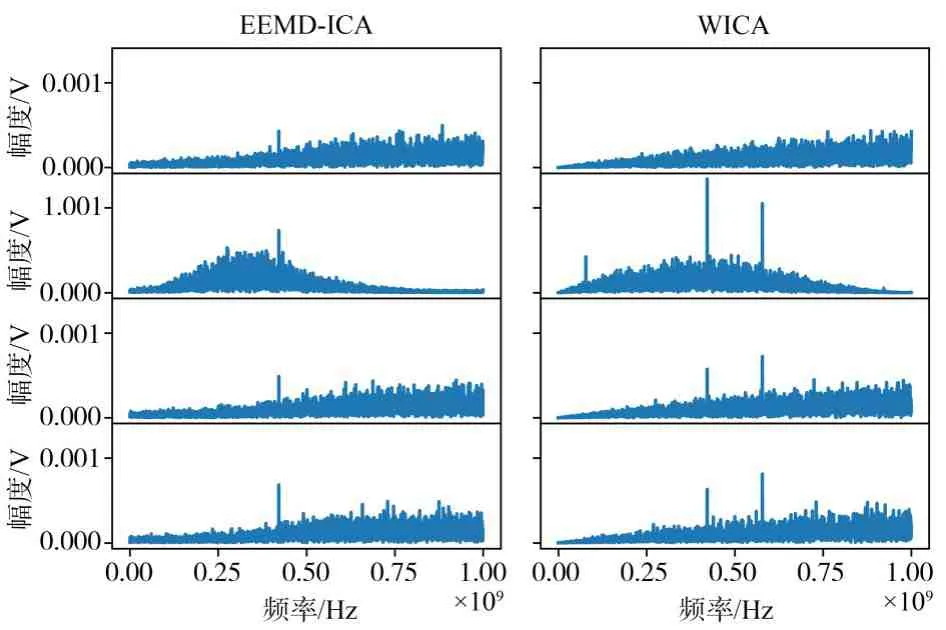
图12 EEMD-ICA和WICA分离ICs频域结果
此外,本文从时域和频域两个方面入手进一步证明WICA 算法的有效性. 根据式(2),从时域角度计算EEMD-ICA 和WICA 的ICs 与观测通道OBs 之间的CRC作为性能指标,这是因为OBs 是ICs 经过混合而来,它们之间存在一定的相关性. 值得注意的是,之所以不采用常规的MSE 作为性能指标是因为现场测试环境下很难得到纯净的辐射源信号,即暗室中得测试结果,难以计算常规MSE 指标. 由图13 可见,总体来看,WICA 的ICs 与OBs 的CRC 都要高于EEMD-ICA 的ICs. 而且WI‑CA 的ICs 都只和一个通道的CRC 高,而与剩余通道CRC 都比较低. 相比而言,EEMD-ICA 的ICs 与各OBs的CRC 仍比较高,这说明EEMD-ICA 分解的ICs 并不彻底,不同ICs 之间仍存在频谱的混叠. 值得注意的是,WICA 的IC1 之所以与OBs 相似性不高,主要是因为它分离出了OBs 中幅值较小的组分(200 KHz),这也说明了WICA有更强的信号分离能力.
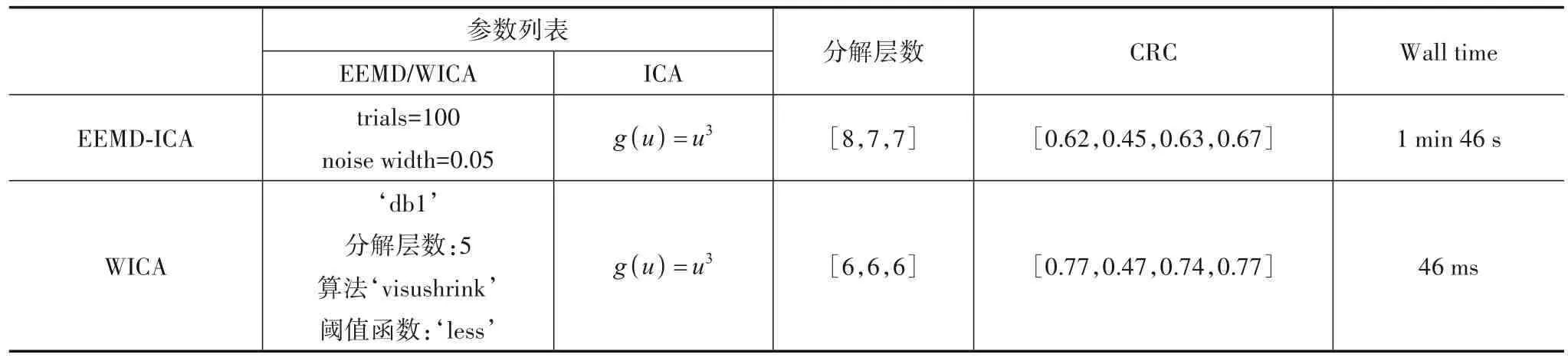
表2 EEMD‑ICA/WICA 算法参数与指标对比
此外,根据式(4),从频率角度计算ICs 之间的相干性,结果如图14 所示. 从图中可见,EEMD-ICA 的IC0-IC1 在400 MHz 以及900 MHz 处有较大的相干性,更糟糕的是IC1 和IC2 在全频段相干性都很高. 而相比于EEMD-ICA,WICA 不同ICs 之间的相干性都比较低,总体低于0.5. 证明了WICA的ICs之间的独立性更好,WI‑CA比EEMD分解地更为彻底.
因此,无论是从时域CRC还是频域Cxy的指标比较都表明:虽然EEMD-ICA和WICA都做到了从3个设备电磁混合信号(OBs)中分离出了4个ICs,解决了多通道欠定盲电磁辐射现场测试分离问题. 但与EEMD-ICA相比,WI‑CA的分离的ICs更为彻底,更能反映源信号的时频特征.
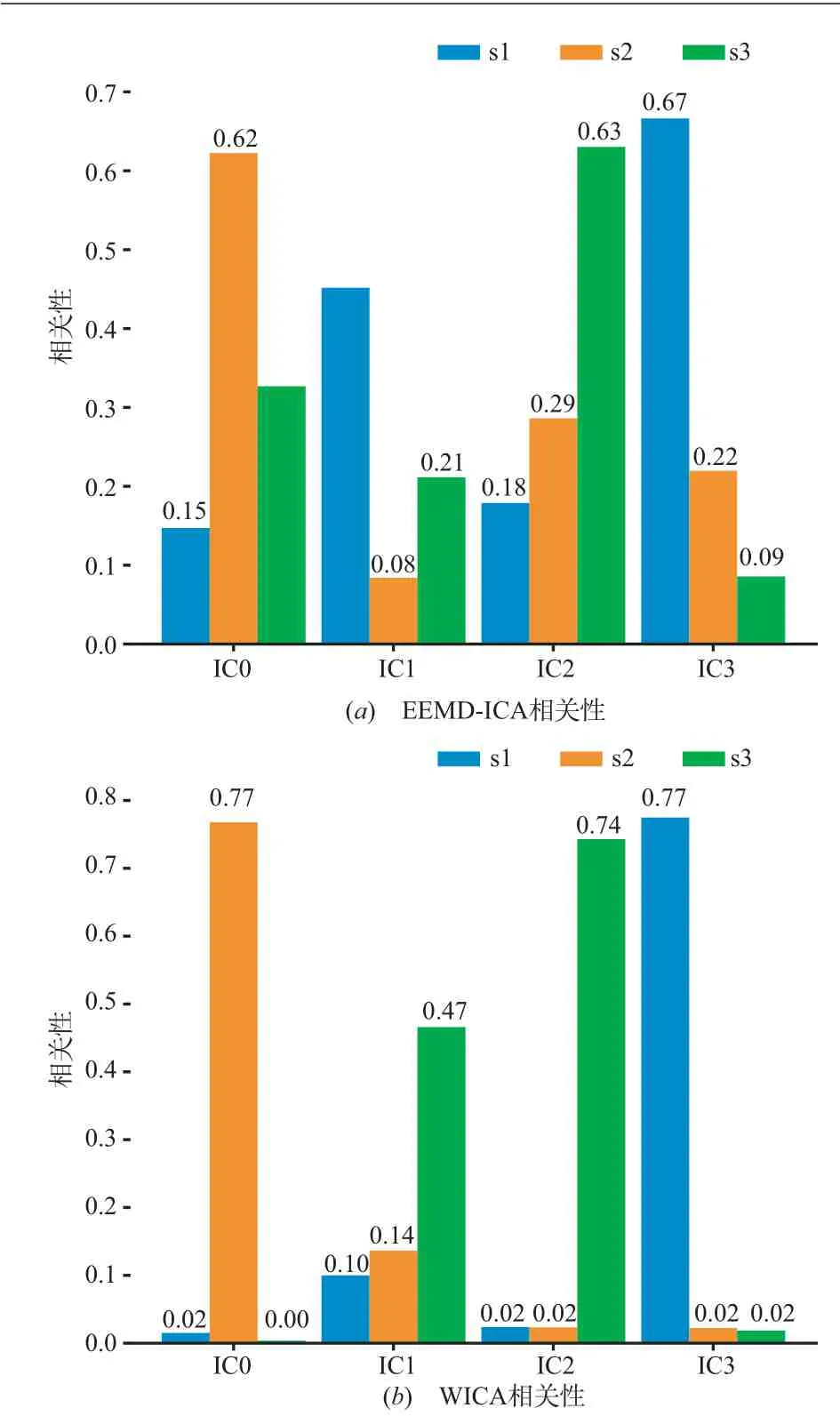
图13 OBs与ICs之间的CRC比较
此外,经实际试验测算WICA 的执行时间是46 ms,而EEMD-ICA 的执行时间是1 min 46 s,经详细分析发现,EEMD-ICA 算法时间损耗主要集中在EEMD 算法模块部分,这是因为EEMD 通过引入高斯白噪声求平均值的方法抑制模态混叠,但这大大增加了数据处理的运算量和运算时间,这对实时性要求很高的现场测试来说,非常不利. 说明WICA 更能满足现场电磁辐射测试实时性的需求. 综上,本文将WICA 和EEMD 的关键参数和性能指标总结在表2 中. 通过比较可以发现,无论从实际应用的角度(wall time)还是算法性能(CRC,Cxy)的比较,本文所提出的WICA 算法都更能满足多通道盲电磁辐射现场分离的需求,可以为设备现场电磁兼容测试提供行之有效的方案.
为了更充分地验证提出算法的有效性,我们以均方误差NMSE 和NCRC 作为衡量指标,将提出算法与FastICA,JADE[20],CuBICA[21]和TDSEP[22]四种竞争算法进行比较. 其中,性能指标NCRC定义如下:
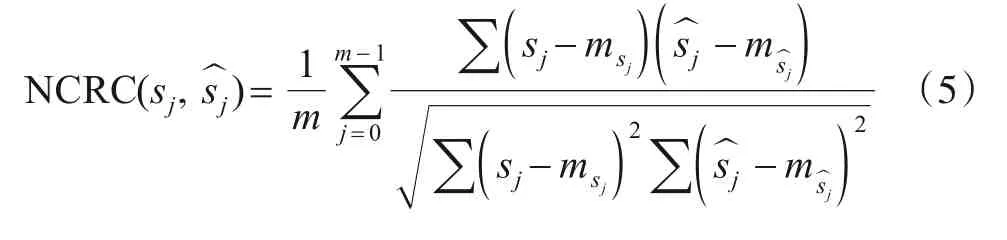

图14 ICs之间的相干性
上述算法关键参数配置如表3所示.
其中,s和̂都是n×m维信号矩阵,n是采样点,m是信号维度,sij是矩阵s中i行的第j列,sj是矩阵s的第j列.考虑到实际测试中源信号s难以获得,本文采用观测信号代替源信号s进行计算.

表3 对比算法参数配置
比较结果如图15 所示,当考虑NCRC 时,WICA 分离结果与观测信号的NCRC 在四种比较算法中最高为0.76,说明提出算法的分离信号更佳. 对于NMSE 指标而言,WICA 算法的均方误差最小. 究其原因,WICA 在进行分解信号筛选时采用的是本文提出的相关性筛选准则,能够有效筛选相关分量,而上述比较算法则是以协方差矩阵特征值作为筛选依据,因此分离性能较差.综上所述,提出算法的两项性能指标都是最好的(NCRC=0.76,NMSE=0.35),充分说明提出算法与竞争算法相比具有更好的稳态分离性能.
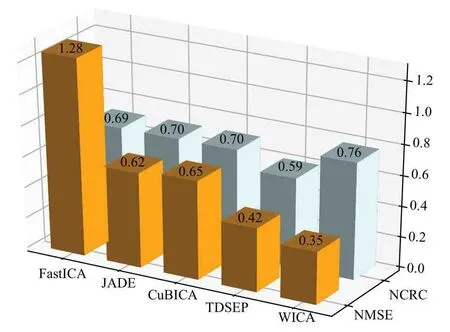
图15 不同算法性能指标比较
4 结论
本文提出了一种基于小波分解、相关性筛选以及独立成分分析的WICA 算法,算法可以应用于大型系统复杂电磁环境下多通道欠定盲电磁辐射信号的分离任务,该方法设计了一种新型的WICA 算法结构,采用小波阈值去噪克服现场噪声对信号分解的影响,利用小波分解分离出多层信号,解决了常规ICA算法的欠定问题,提出了相关性筛选准则,结合小波分解各层之间的频率特点,筛选有效分量,解决了ICA 处理多输入信号时,有效分量容易被高能量低频或高噪声分量掩盖的问题. 为验证提出算法的WICA 方法的有效性,应用实船测试数据对提出的算法展开验证. 通过与已有EEMD-ICA 算法的对比,从定性和定量的角度验证了提出的算法在处理系统级复杂电磁环境下多通道欠定盲电磁辐射的分离问题的有效性和优越性,为系统级虚拟暗室理论提供了新的途径,具有较高的应用价值,当然,算法在实现过程中也存在一定的不足,因为实船测试中采集的电磁辐射信号数据量较大,在进行WICA 处理的时候,耗时较长,后续将从WICA 并行优化的角度出发,对算法的实现进行优化,以提高船舶电磁辐射测试对实时性的要求.

