凹坑局部干扰热环境数值模拟研究
童福林,唐志共,国义军,代光月
(中国空气动力研究与发展中心,四川 绵阳 621000)
0 引 言
当前,由于高超声速飞行器结构和防热设计的需要,飞行器表面不可避免出现凹坑或缝隙等局部间断,如导弹天线窗和防热瓦间隙等。这些凹坑的存在会对流场产生干扰而引起局部热流的陡增,从而给飞行带来极大的安全隐患。因此,对凹坑局部干扰热环境分布规律的研究是十分必要的。
20世纪60年来以来,国内外[1-6]针对凹坑局部热流问题进行了大量的试验研究,并通过对试验数据的相关性分析,拟合出了一些经验或半经验的热流关联公式,但由于关联公式的局限性,在工程应用方面还存在较大的不足。近年,随着CFD技术的发展,数值模拟方法在凹坑局部流动问题中应用越来越广泛[7-8],但目前研究主要集中在凹坑流动的力学特征以及非定常振荡和声学特性等方面,而在凹坑局部热环境数值模拟研究方面做的工作相对较少。
本文通过求解雷诺平均N-S方程,采用NND格式和SST两方程湍流模型,对开/闭式凹坑二维和三维流动情况进行了模拟,得到了凹坑内压力和热流的分布,并将计算值与试验结果进行了比较,分析了开/闭式凹坑在凹坑侧壁影响下局部压力和热流分布的差异。
1 凹坑流动分类
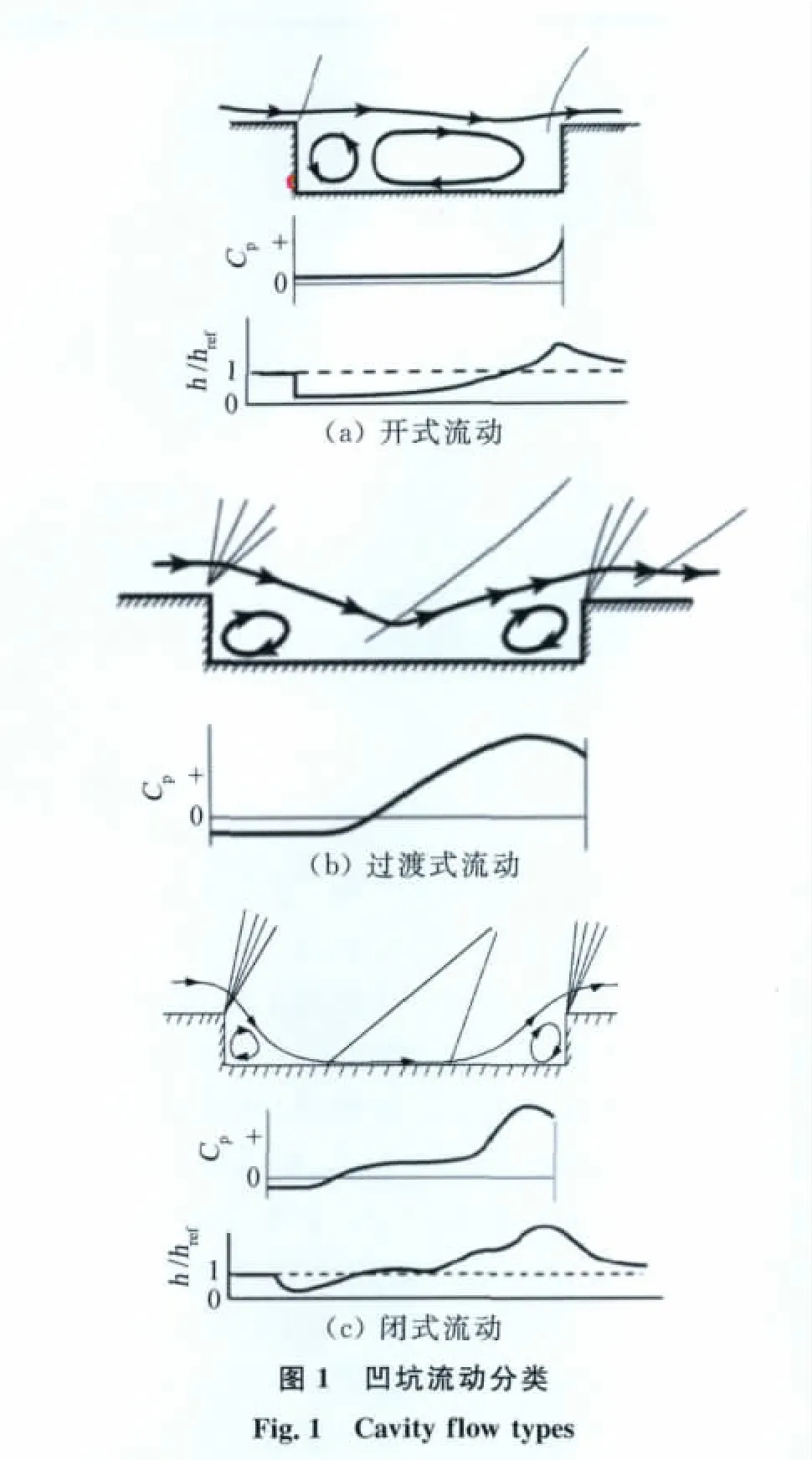
研究表明[1-3],依据凹坑长深比L/H 的不同,凹坑流动可分为三大类:开式流动、过渡式流动和闭式流动,如图1所示[4]。一般取1≤L/H≤10为开式凹坑流动,此时凹坑内部将产生较强的旋涡,坑内压力和热流均逐渐升高,并在凹坑后沿附近达到峰值。L/H≥14时流动为闭式凹坑流动,气流在凹坑前沿膨胀分离后,直接打在凹坑底部,随后向凹坑后沿压缩再附,在凹坑前后沿底部分别产生了旋涡运动,同时凹坑底部中心附近存在着压力和热流平台。对于过渡式凹坑(10<L/H<14),其流动特征界于开式流动和闭式流动之间,但过渡式凹坑流动带有较强的非定常性,在实际应用中一般尽量避免出现。本文主要针对开式和闭式凹坑局部热环境进行研究。
2 数值方法
2.1 控制方程
控制方程采用一般曲线坐标系下三维无量纲守恒型N-S方程:
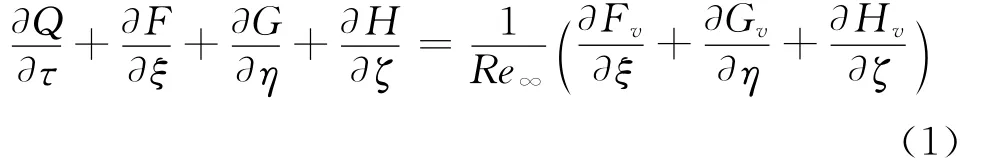
其中Q表示守恒量,F、G和H 表示无粘矢通量,Fv、Gv和Hv表示粘性矢通量。Re∞为基于特征参考长度的来流雷诺数。
2.2 SST湍流模型
本文采用Menter SST两方程湍流模型。控制方程为:
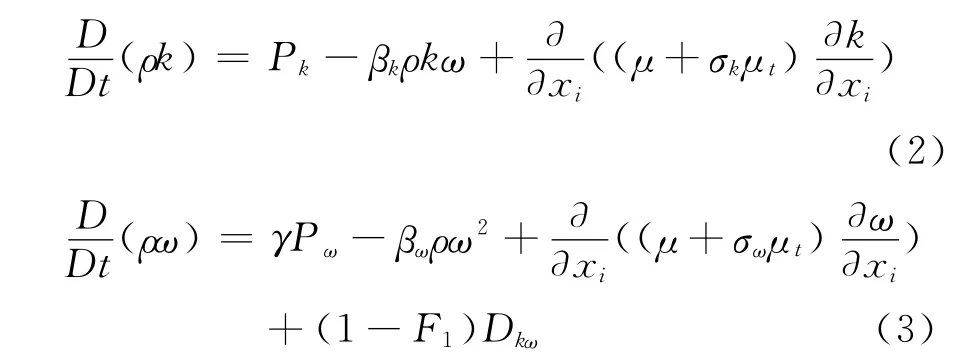
其中Pk和Pω为生成项,βkρkω 和βωρω2为破坏项,Dkω为耗散项混合导致的交叉项,各项具体表达式参考文献[9]。F1为混合函数,形式如下:

模型中各常量均通过混合函数由k-ε方程和k-ω方程中的常数混合生成,具体方式如下:
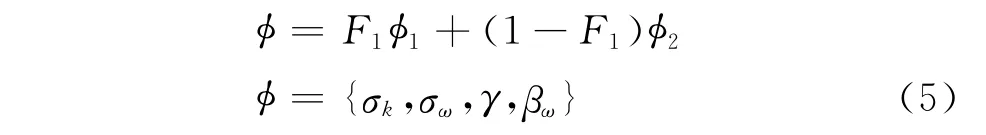
湍流粘性系数μt的计算公式为:
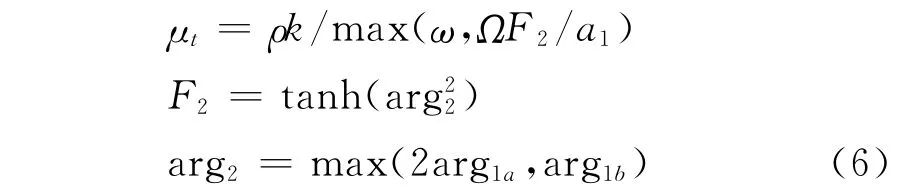
2.3 方程离散
N-S方程采用原始变量型NND格式离散,无粘项计算采用Kim[10]的AUSMPW+格式,粘性项采用二阶中心格式离散。对于定常问题,时间推进采用隐式LU-SGS方法。以ξ方向为例:
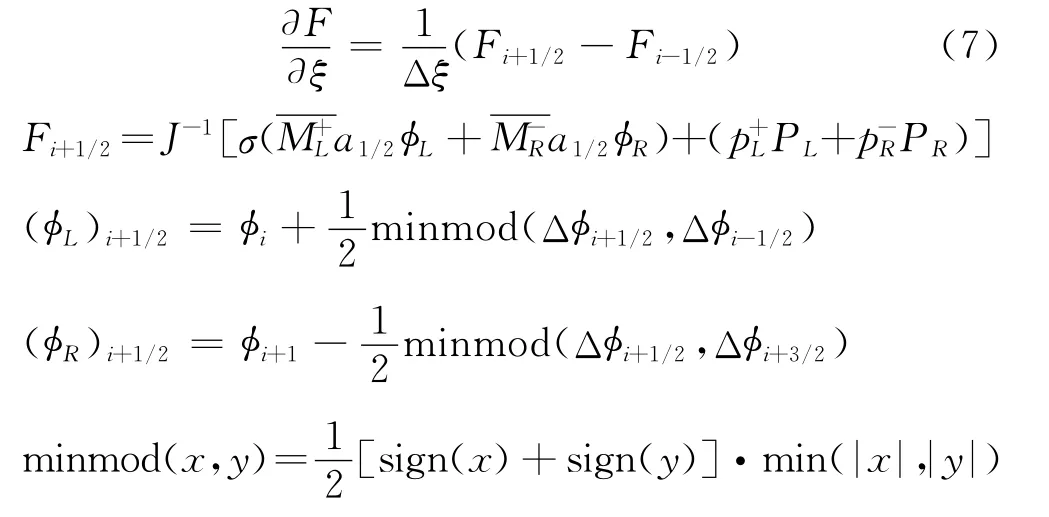

湍流模型方程中无粘项采用一阶迎风格式离散,粘性项采用二阶中心差分格式离散,模型方程与N-S方程非耦合求解。
2.4 计算网格和来流条件
计算模型取自文献[5]中的试验。图2为计算网格。为了准确模拟凹坑内流动分离和再附、激波干扰等复杂现象,本文对壁面、凹坑拐角和剪切层等流动区域内网格进行了加密处理,网格点数为87×43×39(凹坑内)和237×51×75(凹坑外),物面法向第一层网格距离取1×10-6m。由于流动的对称性,这里只对半流场进行计算。
来流条件[5]:迎角α=-11.5°,来流马赫数 M∞=10,来流雷诺数Re∞=0.9×107m-1,来流温度T∞=50K。
流场边界由物面、远场和进出口条件组成。物面边界采用无滑移条件(u=v=w=0)和等温壁条件(Tw=300K)。由于超声速来流,入口和远场固定为来流值,出口边界采用一阶外插得到。
3 结果分析与讨论
3.1 二维情况
为了比较开/闭式凹坑在二维和三维情况下局部流动的差异,本文首先对二维情况下开式和闭式凹坑局部流动进行了模拟。这里的二维情况指的是在没有考虑凹坑侧壁影响下的流动情况,其它来流条件不变。
图3和图4分别给出了开式(L/H=5)和闭式(L/H=30)凹坑内流线及等马赫数云图。可以看到,对于开式凹坑,气流在凹坑前沿膨胀分离后,直接滑过凹坑打在凹坑后壁上压缩、再附和分离,凹坑内存在一个较强的主旋涡,左下角有强度较弱的次旋涡,凹坑内流动马赫数较低;而对于闭式凹坑而言,气流在凹坑前沿膨胀分离后,探底打在凹坑底部,随后沿底部向前流动,并在凹坑后沿附近发生分离、回流和再压缩,因此闭式凹坑左下角和右下角分别出现了两个旋涡,并且由于气流的探底,闭式凹坑内流动马赫数较高。
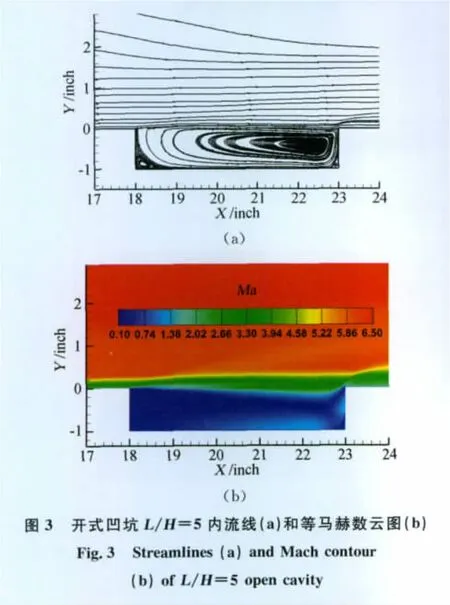
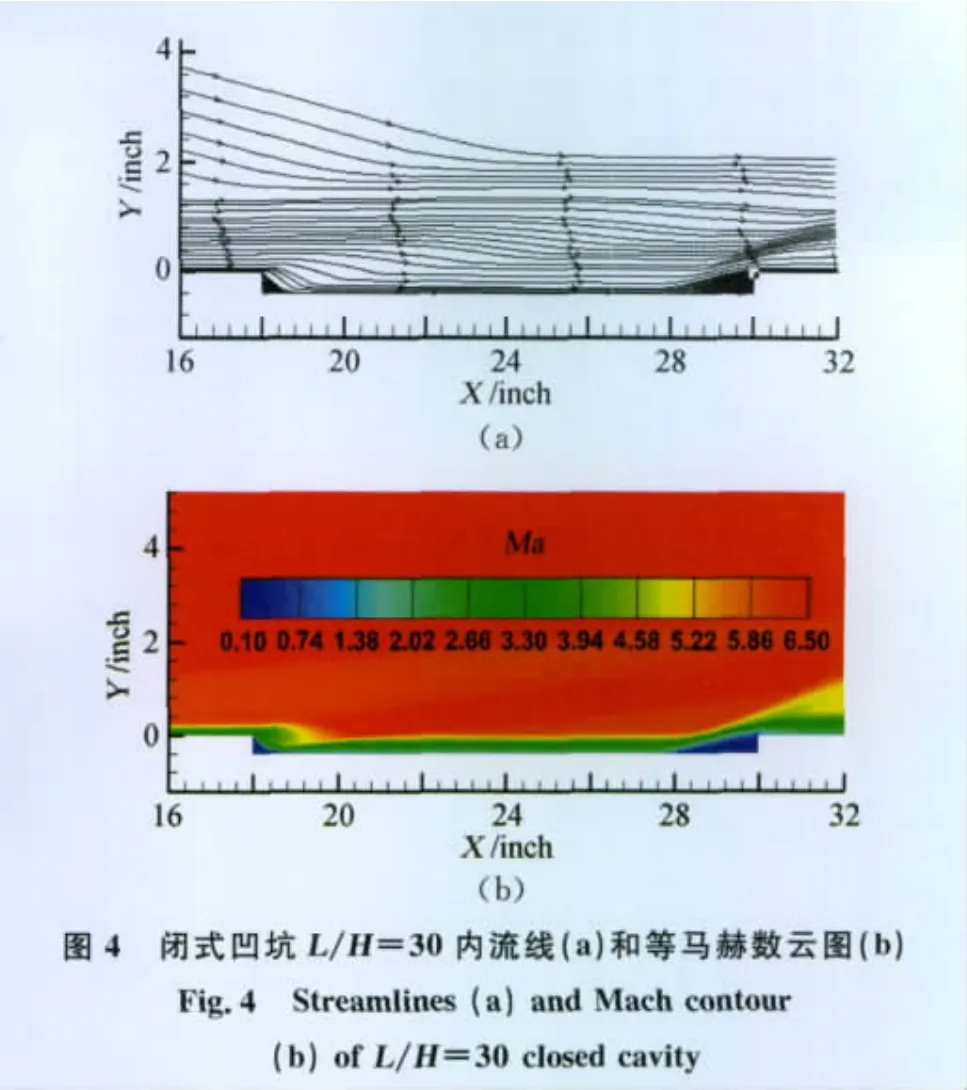
3.2 三维情况
图5(a)和图5(b)分别给出了三维流动情况下凹坑底部压力和热流分布计算结果与试验的比较。
这里的三维流动指的是考虑了凹坑侧壁影响的流动情况。图中P0和Q0为当地无凹坑干扰情况下压力和热流值。可以看到,压力和热流分布的计算结果与试验数据[5]较为吻合。这说明了本文采用的数值方法和湍流模型是可行的,能够模拟出凹坑内局部压力和热流的分布情况。
从图5(a)中压力整体分布趋势上来看,底部峰值压力均出现在底部靠近凹坑后壁的区域,这是由于气流压缩再附的缘故。闭式凹坑流动时,随着气流在前沿膨胀分离后再附于底部,底部压力下降后急剧升高,当气流沿底部流动时,压力出现了一个平台区,它的长度一般依赖于L/H 值[4]。而开式凹坑流动时,底部压力变化相对较小,只是在靠近后沿的区域由于气流压缩后逐渐升高并达到峰值。
从图5(b)中底部热流分布图中可以看到,底部峰值热流同样出现在底部靠近凹坑后壁的区域,热流整体分布规律上与压力分布也较为相似。且闭式凹坑底部热流更为严重些,在底部靠近前沿的区域内热流逐渐升高,到底部中心区域后热流变化趋于平缓,随后在靠近后沿的区域热流急剧升高,峰值热流Q/Q0达到3.0,而开式凹坑底部热流值相对较小,并有2/3的区域热流比值Q/Q0小于0.5。
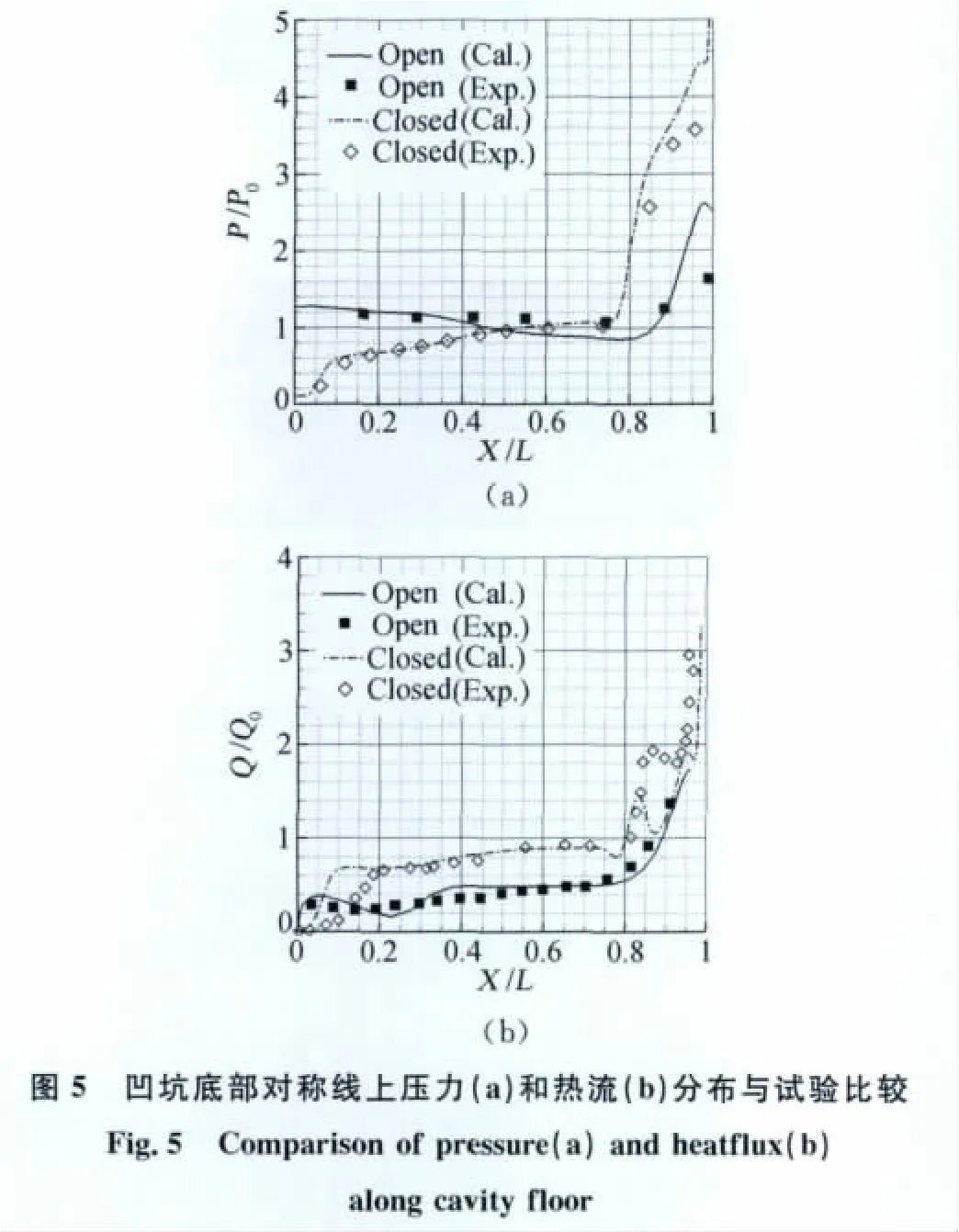

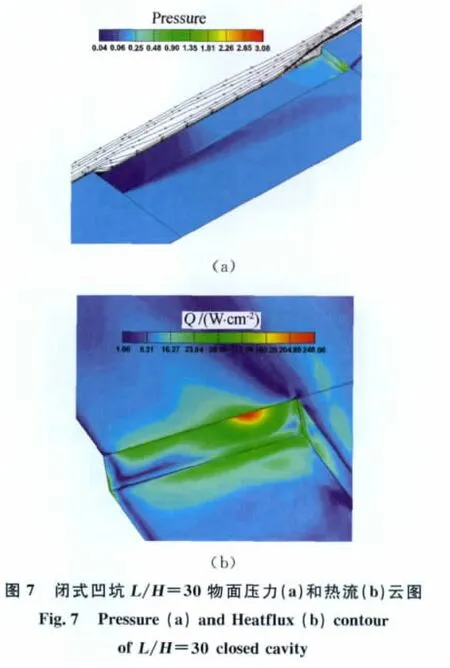
图6和图7分别给出了三维情况下开式凹坑(L/H=5)和闭式凹坑(L/H=30)物面压力及热流的分布云图。
可以看到,在三维流动情况下,由于凹坑侧壁的影响作用,凹坑内气流将发生横向流动。从图6(a)可以看到,气流直接滑过了凹坑,沿凹坑展向存在较为相似的旋涡结构,而在图7(a)闭式凹坑空间流线分布中可以看到,气流探底后沿凹坑底部向下游流动,在凹坑内靠近后沿的区域,由于凹坑侧壁的影响,凹坑下游内产生了较强的横向旋涡流动。这表明开式凹坑在沿后沿展向上主要以二维流动为主,而闭式凹坑内则存在着明显的三维流动特征。
4 结 论
本文通过求解雷诺平均N-S方程,采用NND格式和SST两方程湍流模型,分别对开/闭式凹坑二维和三维流动情况进行了模拟,得到了凹坑内压力和热流的分布,并与试验结果进行了比较。通过计算和分析,得出以下结论:
(1)本文计算得到的凹坑底部压力和热流分布与试验结果吻合较好,计算获得的凹坑流场结构与凹坑流动规律一致,这说明本文采用的数值方法和湍流模型是可行的,能够模拟出凹坑内局部压力和热流的分布情况。
(2)凹坑局部峰值压力和热流均出现在凹坑后沿附近,但闭式凹坑局部热流较开式凹坑更为严重些。在三维流动情况下,由于凹坑侧壁的影响,开式凹坑峰值热流沿后沿展向变化较小,而闭式凹坑峰值压力和热流会离开后沿中心而出现在后沿靠近侧壁的区域。
[1]CHARWAT A F,ROOS J N,DEWEY F C Jr,et al.An investigation of separated flows-part I:the pressure field[J].Journal of the Aerospace Science,1961,28(6):457-470.
[2]CHARWAT A F,ROOS J N,DEWEY F C Jr,et al.An investigation of separated flows-part II:flow in the cavity and heat transfer[J].Journal of the Aerospace Science,1961,28(7):513-527.
[3]NESTLER D E.An engineering analysis of reattaching shear layer heat transfer[R].AIAA Paper 72-717,1972.
[4]EVERHART J L.Supersonic/hypersonic laminar heating correlations for rectangular and impact induced open and closed cavities[R].AIAA Paper 2008-1283,2008.
[5]NESTLER D E.Heat transfer to steps and cavities in hypersonic turbulent flow[R].AIAA Paper 68-673.
[6]唐功跃,吴国庭.二维空腔内的流动及热环境分析[J].航天器工程,1996,5(4):15-22.
[7]候中喜,夏刚,秦子增.三维超声速开式空腔振荡特性研究[J].国防科学技术大学学报,2004,26(6):1-4.
[8]罗柏华,二维高亚声速空腔流激振荡的数值模拟研究[J].空气动力学学报,2002,20(1):84-88.
[9]MENTER F R.Two-equation eddy-viscosity turbulence models for engineering applications[J].AIAA Journal,1994,32(8):1598-1605.
[10]KYU HONG KIM.Accurate computations of hypersonic flows using AUSMPW+ scheme and shock-aligned grid technique[R].AIAA Paper 98-2442.
