含混合储能的铁路10 kV配电网综合能源系统规划
肖 斐,吴命利,何婷婷
(北京交通大学 电气工程学院,北京 100044)
0 引言
随着经济、社会、文化的快速发展,人民生活质量在日益提高的同时,对能源供应质量和能源种类也提出了更高的要求[1]。区域综合能源系统作为一种集成冷、热、电、气等多种能源形式的新型供电系统,目前已受到广泛的关注[2]。已建成的示范性区域综合能源系统包括上海迪士尼度假区示范工程[3]、天津中新生态城[4]、北京延庆光热发电基地[4]、广东佛山冷热电联供微网系统等。通过大量实践表明综合能源系统通过多能生产、能源转换和存储环节可有效提升系统能源使用效率,降低总体经济成本。
在区域综合能源系统规划方面,文献[5]提出一种联合区域综合能源系统管网规划和能源站枢纽规划的双层规划方法,上层规划模型以直流潮流模型和气网潮流模型为基础,下层规划模型以多能源转换模型为基础,以实现多能设备容量配置和线路优化配置。文献[6]提出一种考虑多区域互联协同的分布式能源站规划模型,涵盖了设备类型选择、管道路径规划和多区域间协同优化运行。文献[7]提出一种计及需求响应不确定性的区域综合能源系统协同规划配置方法,利用证据合成理论实现需求响应的不确定性评估,并结合双层规划模型确定最优电价和设备容量配置方案。文献[8]提出一种考虑冷热电多能负荷不确定性的区域综合能源系统鲁棒规划方法。文献[9]提出以综合能源系统建设成本和运行费用最低为目标,且考虑多种能源枢纽架构的规划模型。上述模型主要用多能源之间的转换关系和多能源设备的经济成本计算得到各类设备的最优容量。以光伏与风力发电为典型代表的发电形式存在间歇性、随机性及波动性等缺点,为确保上述系统中的功率平衡、稳定性、电能质量等,必须配备相应的储能系统[10-14]。近年来,混合储能作为一种兼具功率型和能量型的复合储能设备,已成为区域综合能源系统盈利和分布式能源功率平抑的关键环节。
在混合储能容量规划方面,文献[15]基于区域综合能源系统架构,设计一种考虑系统全寿命周期收益的冷、热、电混合储能配置方法,为工程实践提供参考。文献[16]在净负荷功率频谱分析的基础上,提出一种协调蓄电池(BES)与超级电容器(SC)运行的微电网功率分配策略,并以混合储能年综合成本最小为目标建立了容量优化配置模型。文献[17]提出了一种基于集合经验模态分解(EMD)的交直流微电网混合储能容量优化配置方法,该方法以平抑后的负荷功率波动量和年综合成本最小为目标。文献[18]基于离散傅里叶变换方法将孤岛型微电网中的电源负荷不平衡功率进行分频处理,提出频率分断原则以实现混合储能经济优化配置。由上述分析可知,现有的区域综合能源系统规划多以能源均衡分配为约束,有必要考虑混合储能对分布式能源波动量的消纳平抑。另一方面,铁路10 kV 配电网作为保障铁路安全运行的关键,有必要对其开展含混合储能的综合能源系统规划研究,以提升其运行的可靠性和经济性。
综上,本文提出一种含混合储能的铁路10 kV配电网综合能源系统规划模型。首先,针对铁路配电网用能需求设计区域综合能源系统架构。其次,提出一种基于EMD 的光伏出力高频分量提取方法,并联合典型日负荷数据生成考虑多类光伏高频分量平抑的典型场景集。然后,以等值年总成本最低为目标、混合储能和综合能源系统的运行和功率平衡为约束,建立多场景铁路10 kV 配电网综合能源系统优化配置模型,并利用混合整数线性规划算法求解该模型。最后,以我国北方某铁路10 kV 配电网为例分析验证了所提方法的有效性和可行性。
1 含混合储能的铁路10 kV 配电网综合能源系统架构
混合储能是由功率型和能量型储能共同组成的复合储能装置,具有响应速度快、循环寿命长的特点。通过合理配置不同种类的储能容量,可充分利用其在充放电性能和经济性之间的互补特性。鉴于上述分析,有必要在铁路10 kV 配电网规划中引入混合储能系统。通过合理规划SC、BES 和储热(HS)设备的容量,以实现铁路10 kV 配电网光伏出力波动消纳平抑和经济效益提升。另一方面,通过接入热电联产(CHP)设备可满足配电网的多能源需求。
图1 展示了铁路10 kV 配电网综合能源系统内多能设备的物理连接拓扑和多能转换关系。由图可知,综合能源系统包含了燃气锅炉(GB)、CHP、SC、BES、HS 和光伏(PV)设备。鉴于现有配电系统已建设了电网线路和热网管道,本文不考虑从配电网至各用户负荷端传输电、热的管线投资成本[19]。
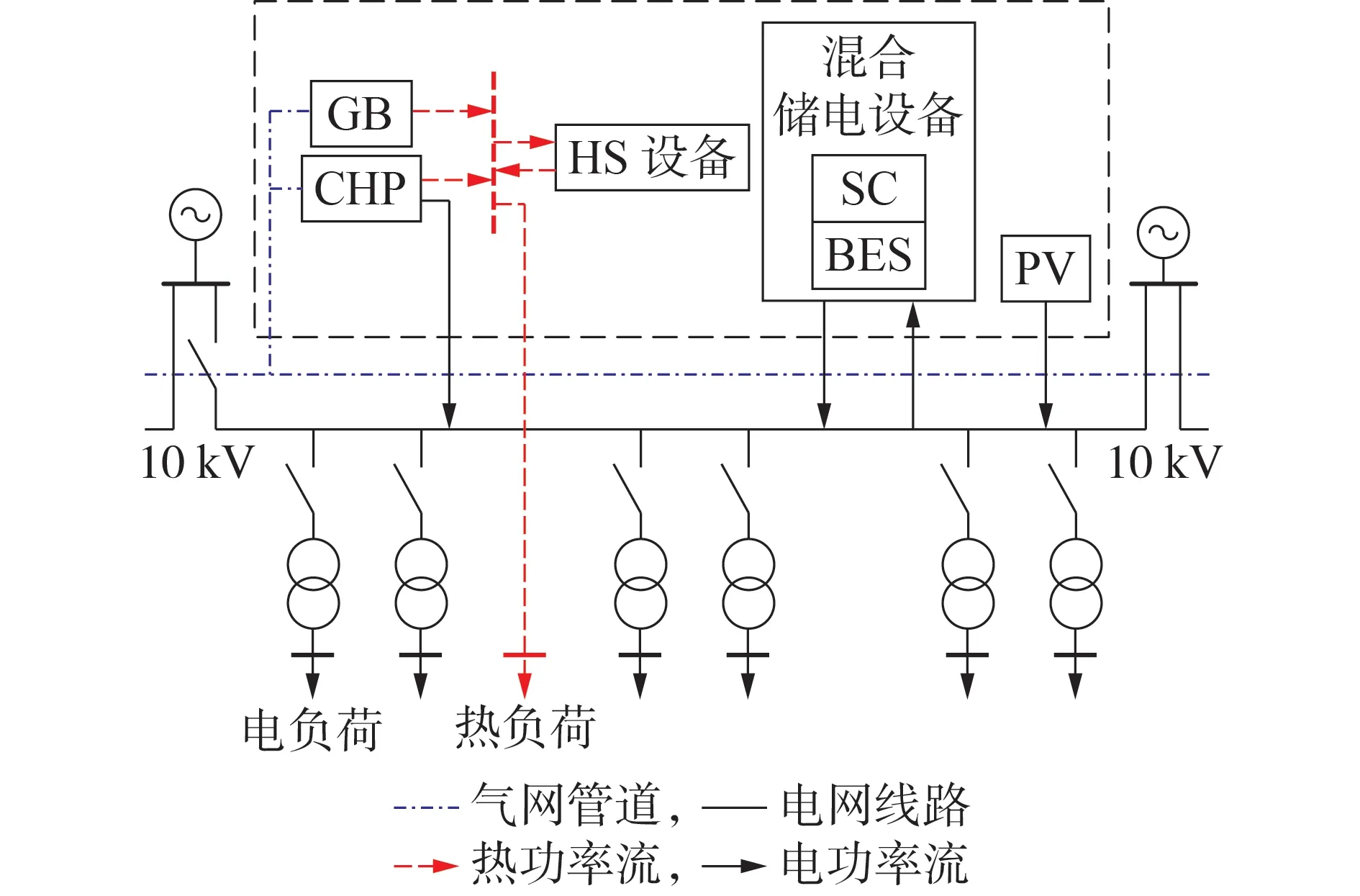
图1 含混合储能的铁路10 kV配电网综合能源系统架构Fig.1 Architecture of railway 10 kV distribution network integrated energy system with hybrid energy storage
2 考虑光伏出力波动水平的场景生成方法
2.1 基于EMD的光伏高频分量提取
考虑到光伏出力的波动性,本文用EMD 方法对光伏出力曲线进行分解,将原始信号分解为一系列不同频率的信号,即固有模态函数(IMF)分量。相较于传统的傅里叶变换方法和小波变换方法,EMD方法无需设置基波分量且计算量较小,在实际工程中使用较为广泛。EMD方法提取IMF的步骤如下[20]。
步骤1:针对含NT个采样点的光伏出力曲线xpv=[xpv(1),xpv(2),…,xpv(NT)],根据曲线的局部极大值和局部极小值可求出上包络xpvup和下包络xpvdown的平均值,如式(1)所示。

通过反复迭代以上步骤可求得具有不同频率的光伏出力曲线,图2 展示了NT=720 时光伏出力曲线和经EMD后的各IMF分量(xIMF1—xIMF4)。

图2 光伏出力曲线和IMF分量Fig.2 Curve of PV output and IMF components
2.2 基于分频参数的光伏高频分量计算

2.3 考虑光伏高频分量的典型场景生成方法
为提升模型的通用性,本文按电、热负荷水平和光伏出力水平设置了3 种典型日。在此基础上,利用EMD 方法提取每类典型日光伏出力曲线的IMF分量,用于计算光伏出力的高频分量。综合考虑需平抑的光伏高频分量,本文将光伏高频分量参数NI最大值设为3,即每一类典型日数据可生成3种含不同光伏高频分量平抑需求的典型场景。综合以上分析,本文共生成3×3=9种典型运行场景。
3 铁路10 kV配电网综合能源系统规划方法
3.1 目标函数
本文所提规划模型以等值年总成本Ccost最低为目标,包含设备投资费用Cinv和系统运行费用Coper两部分,目标函数如下:


3.2 约束条件
含混合储能的铁路10 kV 配电网综合能源系统规划模型的约束条件包括GB、CHP、SC、BES 和HS设备的容量约束、运行约束以及系统能量平衡约束。
1)设备容量约束。
考虑到GB、CHP 设备的占地面积和实际用能需求,设置GB、CHP的规划容量约束分别如下:



3.3 模型求解

模型的具体求解步骤如下。步骤1:统计3种典型日下铁路10 kV 配电系统电负荷、热负荷、光伏发电、电价和气价数据,数据采样周期为2 min;利用EMD 方法将光伏出力曲线分解为IMF 分量;分别设定分频参数NI取值为1、2、3,并计算各场景下的光伏出力高频分量。步骤2:联合3 种典型日下的电、热负荷和光伏高频分量,生成9 种典型运行场景。步骤3:建立考虑多场景的铁路10 kV 配电网综合能源系统规划模型。模型目标函数包括等值年总成本,约束条件包括设备容量约束、设备出力约束、能量平衡约束和光伏高频分量平抑约束。步骤4:基于MATLAB 平台联合YAMIP 和CPLEX 优化工具箱求解所提规划模型,并求得系统最优规划方案和建设运行成本。
4 算例分析
4.1 测试系统及参数介绍
依据我国北方某铁路10 kV 配电系统实际数据进行算例分析,计划建设的GB、CHP、SC、BES 和HS设备的建设投资费用和运行维护费用参数见附录A表A1 和表A2[6]。3 种典型日下的光伏出力、电负荷和热负荷数据见图3,其中3种典型日的光伏出力峰值分别为6.77、10.16、3.39 kW,电负荷峰值分别为112.30、222.84、53.02 kW,热负荷峰值分别为0.60、1.22、0.33 kW。由典型日数据生成的9 种典型场景参数见附录A 表A3。电网分时电价曲线见图4,气价则用天然气热值折算求得为0.28 元/(kW·h)。本文算例测试均在MATLAB 2014a 平台下进行,硬件设备参数为:CPU Intel®CoreTMi7 2.40 GHz,RAM 8 GB,Win 7环境。

图3 典型日电负荷、热负荷和光伏出力曲线Fig.3 Electric load,thermal load and PV output curves in typical day

图4 分时电价Fig.4 Time-of-use electricity price
4.2 规划结果分析
4.2.1 光伏出力曲线高频分量提取
考虑到规划模型中光伏出力高频分量需由SC进行平抑,图5 和图6 分别展示了典型日2 下设置不同的分频参数NI时求得的光伏高频和低频分量曲线。由图可知,随着NI值增大,光伏高频分量曲线幅值逐渐增大,光伏低频分量曲线逐渐平滑。

图5 采用不同分频参数时典型日2下的光伏高频分量Fig.5 High frequency components of PV with different values of NI in Typical Day 2

图6 采用不同分频参数时典型日2下的光伏低频分量Fig.6 Low frequency components of PV with different values of NI in Typical Day 2
4.2.2 考虑光伏波动量平抑的规划结果分析
考虑到综合能源系统规划的经济性和光伏高频分量的平抑需求,求解综合能源系统规划模型,规划结果如表1 所示。该设备容量配置方案的等值年总成本为2.3467×105元,模型计算时间为3616.12 s。

表1 设备容量优化配置结果Table 1 Optimal configuration results of equipment capacity
为分析在最优规划方案下各多能设备的调度运行情况,附录B 图B1—B3分别展示了场景1、场景4和场景7 下的系统购电量、CHP 和GB 设备的出力情况。由图可知,GB 设备主要在电价较低的时段进行供热,该时段内CHP 设备的热出力较小;当电价较高时,CHP 设备出力较高承担了系统大部分电负荷和热负荷,多发的热能由HS设备进行存储。
为分析在最优规划方案下混合储能的充放电及充放热情况,图7(a)—(c)分别展示了场景1下BES、SC和HS设备的出力情况和剩余电量、热量曲线。由图7(a)可知,BES设备在低电价时段充电,高电价时段放电;由图7(b)可知,SC 为实现光伏高频分量平抑,在光伏出力时段进行了频繁的充放电;由图7(c)可知,热储能设备在CHP 低出力时段放热,在CHP高出力时段储存热量,提升了系统的经济效益。

图7 场景1下的仿真结果Fig.7 Simulative results under Case 1
4.2.3 混合储能经济性分析
为分析混合储能对综合能源系统建设运行的经济效益影响,在SC、BES 和HS 混合储能设备未建设的情况下,依据本文算例求得的规划方案为:CHP 设备选型为类型Ⅰ,功率限值为2.09 kW;GB 设备选型为类型Ⅰ,功率限值为1.10 kW,等值年总成本为2.381 6×105元。表1 中设备容量配置方案的等值年总成本为2.346 7×105元。由此可知,混合储能接入综合能源系统能够提升系统整体的经济效益。
4.2.4 CHP设备灵敏度分析
为了分析CHP 设备的投资费用和运维费用对规划方案的影响,可以设置不同的CHP 类型Ⅰ单位容量建设费用和单位容量运维费用,比较其等值年总成本变化情况。设置CHP 类型Ⅰ的单位容量建设成本为4 500 元/(kW·h),逐渐增加该成本并求得不同的规划建设方案,规划结果如表2 所示。由表可知,随着CHP 单位容量建设成本的增加,综合能源系统等值年总成本逐渐上升,CHP 设备的功率限值逐渐减小,热储能设备容量逐渐下降。这是由于模型中CHP 的热电比固定,CHP 多发的热能将存储在HS 装置中,故HS 装置容量与CHP 设备功率呈正相关关系。设置CHP 类型Ⅰ的单位容量运维费用为0.01元/(kW·h),逐渐增加该费用并求得不同的规划建设方案,规划结果如表3 所示。由表可知,随着CHP 运维费用逐渐增加,综合能源系统等值年总成本逐渐上升,CHP设备的规划容量和HS设备容量逐渐下降。

表2 CHP单位容量建设成本灵敏度分析Table 2 Sensitivity analysis of investment cost per unit capacity for CHP

表3 CHP单位容量运维费用灵敏度分析Table 3 Sensitivity analysis of maintenance cost per unit capacity for CHP
4.2.5 模型求解效率分析
为分析模型求解效率,本文分别按2、5、10 min调度时间尺度对模型进行求解,计算时间和计算结果如表4 所示。由表可知,随着调度时间尺度的增大,模型计算时间大幅缩短。由于规划模型中调度时间尺度存在差异,所以光伏高频分量等模型参数不同,造成各等值年总成本存在差异。

表4 模型计算时间和计算结果Table 4 Calculation results and calculation time of model
5 结论
本文以铁路10 kV 配电系统为研究对象,建立了含混合储能的铁路10 kV 配电网综合能源系统规划模型。首先,采用EMD 方法有效提取了光伏曲线的IMF 分量,并计算得到不同分频参数下需平抑的光伏高频分量。其次,将光伏高频分量联合典型日电、热负荷水平和光伏出力水平生成典型场景。然后,基于多能设备的运行和成本参数建立含混合储能的综合能源系统规划模型,并将需平抑的光伏高频分量作为SC 的充放电功率参考值。最后,基于我国北方某铁路10 kV 配电网实际量测数据,验证了所提模型的有效性和可行性。通过仿真分析可知,混合储能接入综合能源系统能有效平抑分布式能源功率波动,并提升系统整体的经济效益。
附录见本刊网络版(http://www.epae.cn)。

