单稳态声学超材料吸收器动力学特性

杨 森，冯进钤，党 慧，鲁甜甜

(西安工程大学 理学院，陕西 西安 710048)

0 引 言

传统吸声材料中的多孔材料和纤维材料对中、高频率范围的声波具有良好的吸收效果，但对低频声波宽带吸收较差。为此，学者们提出了在吸收器中放置柔性板或增加柔性结构[1-2]，或者使用多层微穿孔板或薄膜[3-5]等方案，然其复杂结构限制了它在深亚波范围的低频吸收效果。

近年来，具有设计简单、质量轻、主动吸声等超常物理特性的声学超材料引起了噪声控制领域学者的密切关注。基于局域共振[6]基本理论，具有等效负质量密度[7]、负模量[8]、负折射特性[9]的声学超材料相继被开发，诱发产生高效低频声吸收或者声隔离等现象。同时，学者们还利用该理论研发了板型、薄膜型等各种各样声学超材料[10-11]，对这类材料进行恰当设计便可在深亚波范围实现良好的吸收效果。然而受最小结构的限制[12]，这类线性声学超材料的吸收带宽实质上是个窄带[13]。非线性共振、跃迁、分岔、混沌等非线性动力学现象，有望为非线性声学超材料中声波传播提供新机理，实现低频、宽带、高效的吸收。KHAJEHTOURIAN等[14]应用转移矩阵法，推导出有限应变和无穷小应变运动情况下，具有几何非线性[13]弹性超材料光杆的色散带隙。FANG等研究了非线性声学超材料(简称：NAM)弹性波传播特性，给出了混沌带调控弹性波的新机理[15]，并从理论与实验两方面，描述了一维和二维非线性声学超材料混沌带抑制机理[16]，打破了非线性声学超材料声波传播的带宽限制，为非线性声学超材料的设计和实际应用提供了理论基础。LI等在线性声学超材料中引入磁场，设计出具有物理非线性效应的单稳态声学超材料吸收器，为解决低频噪声控制指明了方向[17]。然而单稳态吸收器在低频范围的吸收带宽较窄，并未达到预期的吸收效果。

通常情况下，谐波平衡法和摄动法分别用来解决强、弱非线性问题[18]。为了更好地满足单稳态吸收器实际应用的需求，针对其低频吸收带宽较窄，以及如何扩大深亚波范围内的低频吸收的问题，本文采用L-P方法，研究平面波激励作用下单稳态吸收器的主谐波响应特性，解释了跃迁现象的产生，找到了弱非线性是导致系统吸收带宽较窄的原因，通过增强系统的非线性扩大低频吸收宽带，为单稳态声学超材料吸收器模型的优化设计提供理论支撑。

1 单稳态吸收器模型

在平面薄板中心粘贴1个磁质量块制作成板型声学超材料(简称：AMM板)。在磁质量块同轴、对称位置，上、下两侧各放置1个磁场，且磁场对质量块产生引力作用，固定AMM板和2个外部磁场，组成如图1所示单稳态声学超材料吸收器模型。

图 1 单稳态声学超材料吸收器模型Fig.1 Monostable acoustic metamaterial absorber model

声音在空气中以声波的形式向前传播。当平面波从正上方垂直入射吸收器时，系统发生受迫振动，AMM板将入射平面波反射、损失、透射，形成反射波、透射波，如图2所示。

图 2 AMM板两侧波分布Fig.2 Wave distribution on both sides of AMM plate

透射波进入到吸收器的封闭后腔，腔内空气的局域振动将透射波消耗殆尽，实现吸收。当系统发生共振时，消耗最大、吸收效果最好。在时间域上，单稳态声学超材料吸收器的动力学方程为[17]

(K+ρcβ2S/D+k1)x(t)+k3x3(t)=

2βSpin(t)

(1)

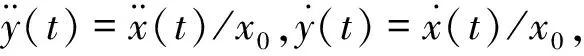
(2)

式中：

显然，方程(2)是典型的受谐波激励的Duffing型振动方程[18]。

2 吸收器主谐波响应

假设平面波激励频率Ω接近于吸收器的固有频率ω0，即Ω≈ω0，此时系统产生主谐波响应。考虑到磁场和薄板产生的恢复力是非线性的，引入小参数ε(0<ε<<1)，并把系统的恢复力和平面波激励看成是对系统的摄动[19]，方程(2)可以写成

(3)

(4)

Ω(ε)=ω0+εω1+ε2ω2+…

(5)

(6)

(7)

运用欧拉法[20]，解得齐次线性微分方程(6)的通解为

(8)

式中：A为振幅；φ为位相。将通解式(8)代入式(7)中，消去久期项可得

(9)

方程(9)为系统(2)的频率-振幅响应方程，刻画了系统的主谐波响应频率ω1与振幅A之间的关系。

在主谐波响应情形下，求解系统质量块振动的位移响应。通过消去久期项，方程(7)可改写为

(10)

(11)

由展开式(4)，得系统(2)的主谐波响应的一次近似解为

(12)

式中：第一项表示线性状态时的色散解；第二项为方程的一个特解，第三项表示存在ε2高阶无穷小量的误差。

针对单稳态声学超材料吸收器低频吸收带宽较窄的问题，在弱非线性和弱激励的阻尼情形下，利用L-P方法求得单稳态声学超材料吸收器振动的频率-振幅方程(9)及位移响应的一阶近似解(12)。

3 数值仿真

固定部分系统参数为ω=1.2,μ=0.05,f=0.05。考虑非线性强度对系统频率-振幅响应的影响，分别取γ=0.01和0.1，由方程(9)给出了系统的频率-振幅响应曲线，如图3(a)所示。其中黑色实线和虚线分别表示拟线性与非线性情形。从图3(a)可以看出，当γ=0.01时，系统表现为弱非线性特性。在拟线性状态下，系统振动频率-振幅响应曲线关于ω1=0具有轴对称性。对于上述渐硬弹簧特性系统，非线性特性导致系统的频率-振幅响应曲线向右弯曲。当平面波激励的振幅增大，频率-振幅响应曲线向右弯曲越大(即偏离轴线ω1=0就越大)，多值性、跃迁等现象越明显。

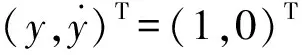
(a) 频率-振幅响应曲线

(b) 位移响应曲线图 3 系统(2)的频率-振幅响应与位移响应Fig.3 Frequency - amplitude response and displacement response of system (2)

为了进一步讨论非线性对单稳态声学超材料吸收器吸收效果的影响，图4给出了在不同非线性强度下系统的频率-振幅响变化曲线。此时，取Y=0.001时的响应作为系统线性状态时的响应。图中蓝色曲线表示拟线性状态时系统的频率-振幅响应，三条虚线分别表示非线性强度为0.5、1.5、2.5时对应的频率-振幅响应。

图 4 不同非线性强度下频率-振幅响应曲线Fig.4 Frequency-amplitude response curves for different nonlinear intensities

从图4可以看出，随着非线性强度的不断增强，系统的频率-振幅响应曲线向右偏移的程度逐渐增大，多值性、跃迁现象等非线性特性更加明显。同时，吸收器在低频范围的吸收带宽相对增宽。因此，增强系统的非线性能够扩大吸收器低频范围的吸收带宽，增强吸收效果。

4 结 论

1) L-P法的近似解曲线与龙格-库塔法的数值解曲线吻合较好，验证了理论推导的正确性。

2) 增强非线性能够扩大了吸收器的低频吸收带宽。增强系统非线性，能够扩大吸收器低频吸收带宽展望。

3) 下一步研究工作将非光滑或不连续等强非线性结构引入声学超材料模型中，以增强吸收器的结构非线性，以期扩展模型在低频吸音中的带宽，提高声学超材料的吸音效果。