改进的布谷鸟搜索算法对支持向量机参数优化

顾佳鑫，贺兴时, 刘 青

(西安工程大学 理学院， 陕西 西安 710048)

0 引 言

1995年，CORTES等学者基于VC维理论和结构风险最小原则(SRM)，提出了支持向量机理论，将需要处理的分类问题转化为凸二次规划问题[1]。目前,已被广泛应用到智能交通[2]、金融预测[3]、生物医学和图像处理[4]等领域。

虽然SVM具有训练速度快和精确度高的优点，但SVM的性能受模型参数惩罚因子C和核函数的参数σ的影响[5]。因此，如何选择这2个参数是SVM研究的热点和难点。传统的SVM参数优化方法为网格搜索法、实验法、交叉验证法[6]和梯度下降法[7]。网格法和实验法耗时长；交叉验证法计算量大，难以实现2个以上的参数选取；梯度下降法对初始值选择敏感，实验结果误差大。因此，设计高效的参数寻优方法是目前的研究重点。

群智能算法在参数优化方面具有较强的并行处理能力，同时具有全局寻优的优点，故常用于SVM的参数优化[8]。具有代表性的为粒子群算法(PSO)[9]、人工鱼群算法(AFSA)[10]、人工蜂群算法(ABC)[11]、萤火虫算法(FA)[12]、蝙蝠算法(BA)[13]、花授粉算法(FPA)[14]和布谷鸟搜索算法(CS)[15]等。

针对原始布谷鸟搜索算法易陷入局部最优解、收敛速度慢、求解精度低的问题，宋庆庆等将混沌序列引入到布谷鸟搜索算法中来初始化鸟窝位置，增加布谷鸟种群多样性[16]；陈程等提出了动态权重改变自适应概率的双重搜索布谷鸟算法(DECS)，通过在寻优过程中引入的新型步长因子以及记忆策略，实现算法双重搜索模式的能力[17]；张珍珍等将多阶段动态扰动引入到布谷鸟搜索算法中，并提出融合正弦余弦和种群初始化策略的布谷鸟算法[18-19]。该算法提高了求解精度，具有更好的优化性能。但上述文献都没有提到改进后布谷鸟搜索算法的应用问题。

为了提高原始布谷鸟搜索算法的寻优能力，本文提出改进的布谷鸟搜索算法(GFCS)：用动态发现概率P代替固定发现概率Pa，自适应地调整布谷鸟莱维飞行的步长控制因子α，在布谷鸟随机游走更新公式中改进动态惯性权重w*；利用GFCS算法优化SVM的惩罚因子C和核函数参数σ解决SVM参数选择盲目的问题，并和传统的SVM、粒子群算法优化SVM、萤火虫算法优化SVM和布谷鸟搜索算法优化SVM进行比较。

1 支持向量机

支持向量机的原理是建立一个分类超平面作为决策面，使得正类和负类样本间隔最大化。将大小为l的训练样本集{(xi,yi),i=1,2,…,l}分为2类：如果xi∈Rn属于第1类，则标记(yi=1)为正；如果xi∈Rn属于第2类，则标记(yi=-1)为负。其中Rn为样本空间的维数[1]。可求得最优分类超平面：

(1)

式中：w为超平面法向量；b为阈值；C为惩罚因子；ξi为松弛变量；φ(xi)为映射函数。引入Lagrange函数,得到式(1)的对偶问题：

(2)

求解式(2)得到最优分类函数：

(3)

式中：ai(i=1，2,…,l)T为Lagrange乘子，K(xi,xj)=φ(xi)Tφ(xj)为核函数。本文采用径向基核函数作为SVM模型的核函数，表达式为

K(xi,xj)=exp(-‖xi-xj‖2/2σ2)

其中σ为核函数参数。

2 布谷鸟搜索算法及改进

2.1 原始布谷鸟搜索算法

布谷鸟搜索算法起源于布谷鸟孕育雏鸟的行为。一些布谷鸟在生产时会将自己的蛋放入百灵鸟、黄莺等宿主鸟的巢中，让它们代替自己喂养雏鸟。当宿主鸟发现鸟蛋来源不明，就会抛弃这些外来的鸟蛋或者重新筑巢。为了模拟布谷鸟的孕育雏鸟行为，YANG等提出了以下3条理想规则[20]：

1) 布谷鸟一次只产下一个蛋，并随机选择鸟窝来孵化；

2) 最好的鸟窝将被保留到下一代；

3) 可选择的鸟窝数量N是固定的,宿主鸟发现外来鸟蛋的概率Pa∈[0,1]。

基于以上3个理想状态，YANG等采用式(4)更新下一代鸟窝位置[20]:

i=1,2,…,N

(4)

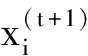
(5)

式中：α0为常数，一般取0.01;xb为当前最优解。

L(λ)～μ=t-λ(1<λ≤3)

(6)

由式(6)可知，布谷鸟在寻窝过程中，其飞行路径变化为带有重尾的概率分布，使得布谷鸟飞行路径表现出了莱维飞行的本质，即在寻优路径中频繁的短步长偶尔会出现长步长。采用式(7)计算莱维随机数[21]：

(7)

式中：μ和v服从标准正态分布；β=1.5，

结合式(4)～(7)，CS算法通过莱维飞行采用式(8)更新鸟窝位置：

(8)

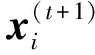
(9)

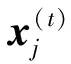
2.2 改进的布谷鸟搜索算法(GFCS)

2.2.1 动态调整发现概率

在原始布谷鸟算法中，用固定的发现概率Pa=0.25控制全局搜索和偏好随机游走，不利于全局搜索和局部搜索之间的平衡。本文提出动态发现概率P代替固定发现概率Pa提高算法寻优性能

(10)

式中：t为当前迭代的次数；T是最大迭代次数。P随t的变化如图1所示。

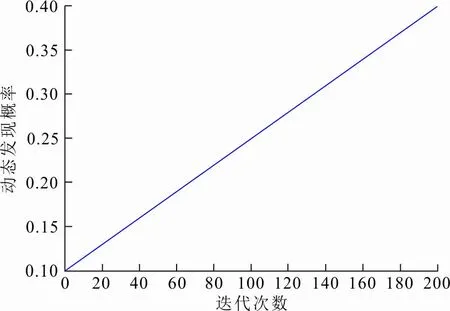
图 1 动态发现概率变化Fig.1 Change of dynamic discovery probability

由图1可以看出，动态发现概率P在[0.1,0.4]之间随迭代次数不断增大。迭代前期以较小的P进行全局搜索;随着迭代过程的进行，P不断增大，直至迭代后期；当P相对较大时，帮助算法在靠近全局最优解时进行局部精细搜索，提高算法的运算精度和搜索效率。

2.2.2 自适应调整步长

针对原始布谷鸟搜索算法寻优精度低的缺点，通过自适应地调整布谷鸟莱维飞行的步长因子α,使得莱维飞行步长随迭代的进行不断减小。在寻优初期拥有较大的步长因子，从而扩大算法前期的搜索空间，提高全局寻优能力；在寻优过程中，步长减小，提高算法局部搜索性能。基于上述分析，将式(7)的α0=0.01改成:

(11)

α0的变化如图2所示。由图2可以看出，α0的值随着迭代次数非线性递减。迭代前期α0的值较大，衰减速度较快，有利于提高算法全局寻优能力，保证算法前期收敛速度快；迭代后期α0的值逐渐减小，衰减速度放缓，提高算法的局部搜索精度。从而将式(8)更新为：

(12)

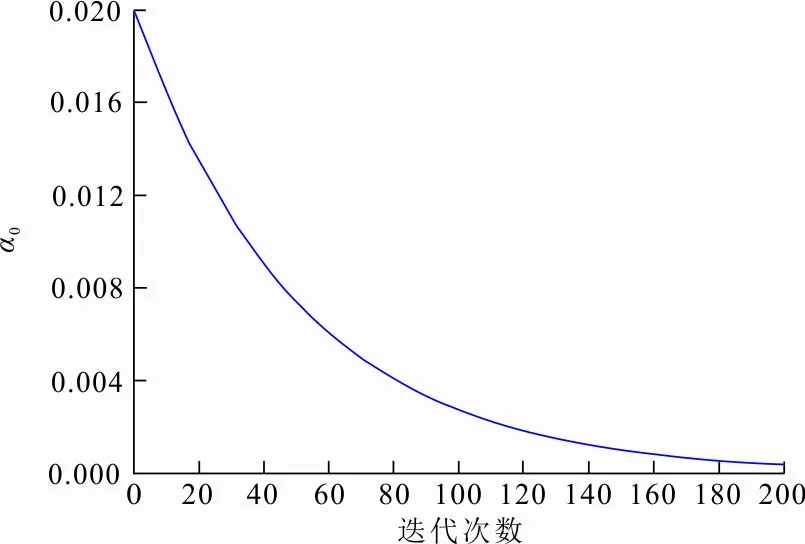
图 2 α0变化曲线Fig.2 Change of α0

2.2.3 动态惯性权重的偏好随机游动

在原始布谷鸟算法的偏好随机游动环节中，采用固定上一代鸟窝位置的更新方式，见式(9)，容易造成算法在迭代后期陷入局部最优值。本文在上一代鸟窝位置处引入动态惯性权重w*，灵活地将上一代鸟窝位置与迭代过程动态联系起来。

(13)

式中：t为当前迭代的次数；T是最大迭代次数。w*的变化如图3所示。

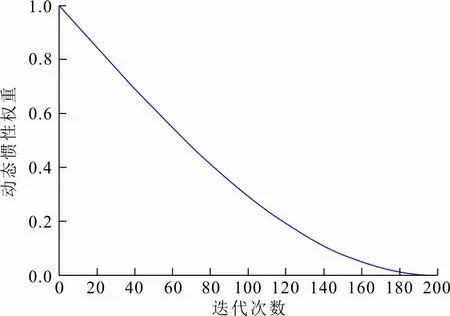
图 3 动态惯性权重w*变化Fig.3 Change of dynamic inertia weight w*

通过图3可以看出，w*在(0,1)之间随迭代次数非线性递减，即随着迭代次数增加，w*逐步减小。在迭代前期，给上一代鸟窝位置赋予相对大的w*，使上一代鸟窝具有更大的作用能力与范围，帮助布谷鸟算法在前期扩大搜索空间，广泛寻找全局最优解；到迭代后期，算法接近最优解时，对上一代鸟窝位置采用相对较小的w*，有效地削弱了上一代鸟窝的保留信息，帮助布谷鸟算法有效跳出局部最优，使布谷鸟个体具有更好的局部寻优能力。将式(9)更新为

(14)

3 GFCS算法对SVM参数优化

GFCS算法在优化SVM参数时，将待优化的参数组合(C,σ)模拟为鸟窝，具体步骤如下：

1) 原始数据集为训练集和测试集，并进行数据归一化。数据归一化公式为

(15)

式中：x、x*分别为归一化前后的样本值；xmax、xmin分别为样本数据中的最大、最小值。

2) 初始化参数。包括布谷鸟种群规模、布谷鸟鸟窝的位置、最大迭代次数、步长因子，被发现概率Pa、参数取值上下界及自变量(惩罚因子C和核函数的参数σ)等。

3) 随机分布鸟窝(C,σ)。采用式(16)作为布谷鸟鸟窝位置的适应度函数，并计算鸟窝的适应度值

(16)

式中：t为当前迭代的次数；a(t)为第t次迭代分类准确率。

4) 比较适应度值，保存当前最小适应度值及对应的鸟窝位置xi。

5) 根据改进后布谷鸟搜索式(12)、(14)更新鸟窝位置xi，并计算适应度值。

6) 产生一组随机数，与被发现概率Pa进行比较：若随机数小于被发现概率，则随机改变鸟窝位置；否则，保持原鸟窝位置不变。更新后的鸟窝位置有可能超出解空间范围，需要将其限制在解空间内：

(17)

式中：xmin和xmax分别为解空间的最大值和最小值i=1,2,…,n。

7) 比较适应度值，找到当前最优解并保留原最优鸟窝位置。

8) 若达到最大迭代次数或满足停止迭代条件，则转至9)；否则转至2)继续迭代。

9) 输出最小适应度值并保留最优鸟窝，即得到最优参数组合(C,σ)。

10) 将输出的最优参数C,σ进行SVM模型的训练和测试。

4 实验结果及分析

实验在Matlab环境下实现，硬件配置为Windows 10操作系统，4 GiB内存，1 TiB硬盘，i7-7500和3.1 GHz主频CPU的计算机。

4.1 GFCS算法性能

为了分析GFCS算法的优化性能，选择6个常用的基准测试函数进行测试。其中Ackley、Rastrigin、Griewank为具有多个局部最小值的多峰函数，用于测试算法跳出局部极值，避免陷入局部最优的能力；Schwefel's2.2、Sphere、Sum square为单峰函数，用于测试算法的优化精度和收敛速度。所选择的6种函数设置见表1。

本次实验将提出的GFCS算法与PSO算法[22]、FA算法[23]、CS算法[20]进行比较。参数设置如表2，实验结果如图4所示。

表 1 基准测试函数Tab.1 Benchmark function

表 2 算法参数设置Tab.2 Algorithm parameter settings

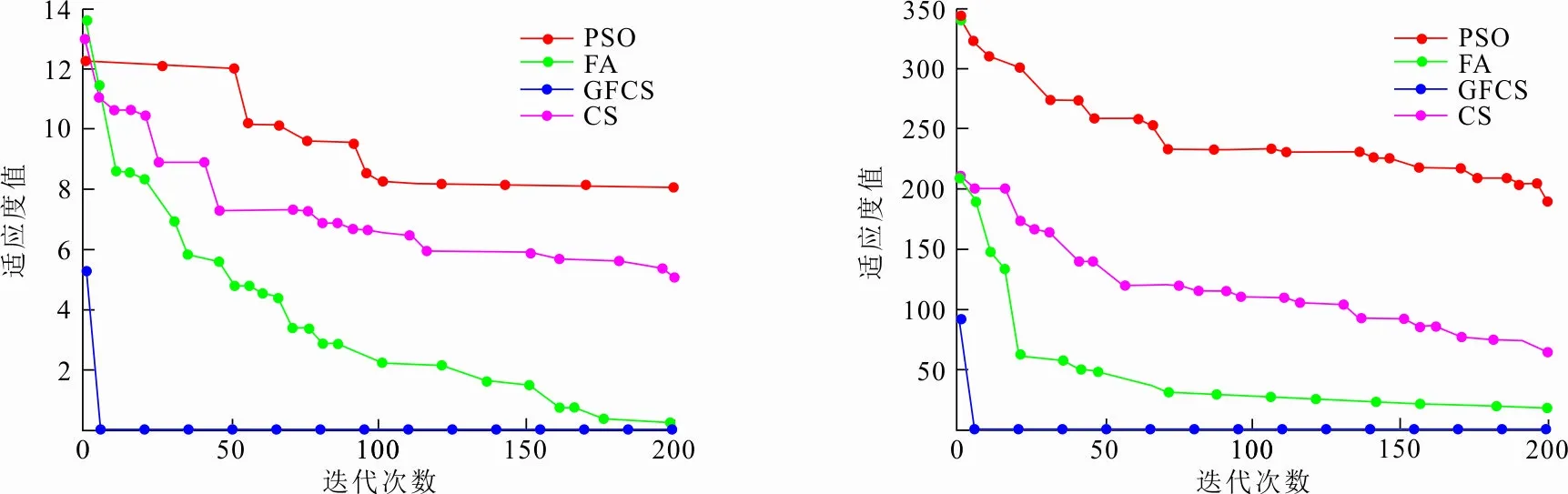
(a) Ackley函数收敛曲线 (b) Rastrigin函数收敛曲线

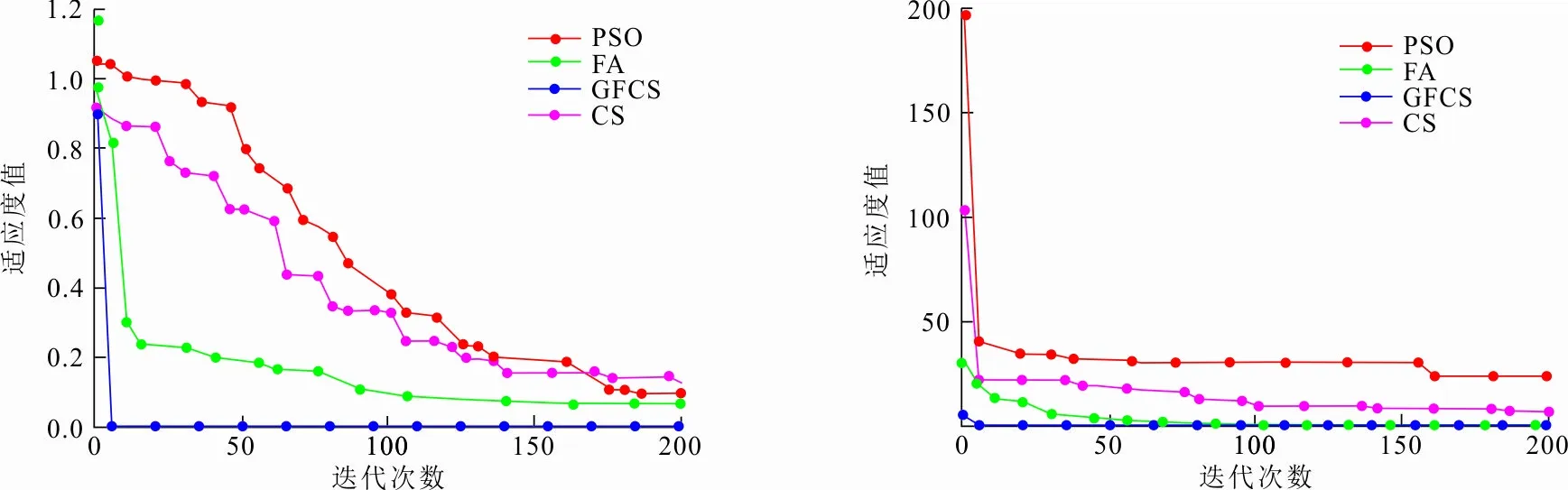
(c) Griewank函数收敛曲线 (d) Schwefel′s2.2函数收敛曲线

(e) Sum square函数收敛曲线 (f) Sphere函数收敛曲线图 4 不同算法在6种测试函数上收敛曲线Fig.4 Convergence curves of different algorithms on six test functions

4.2 GFCS算法优化SVM参数实验

为了验证GFCS算法对SVM的参数优化的有效性，选用径向基核函数作为实验核函数，优化对象为惩罚因子C和核函数的参数σ。采用UCI数据库中的标准数据集测试模型性能，实验数据集描述如表3所示。

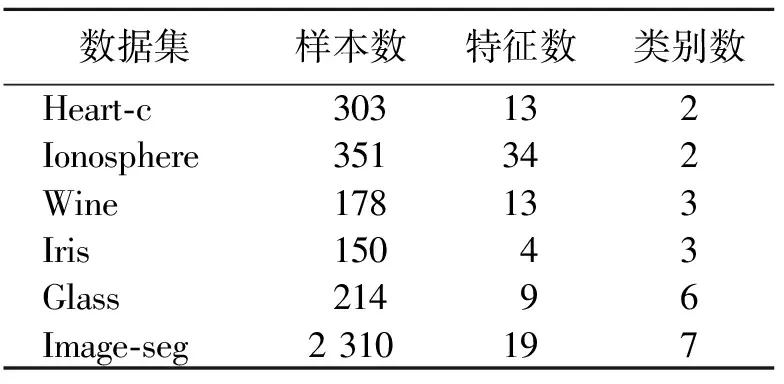
表 3 实验数据集描述Tab.3 Description of experimental data sets

从图4可以看出：GFCS算法收敛速度、稳定性和寻优能力明显高于PSO、FA、CS等算法，并且GFCS算法适应度值最低。表明GFCS算法全局寻优能力较强，不易陷入局部最优解。

实验中，选取未优化参数的SVM、基于粒子群算法的SVM(PSO-SVM) 、基于萤火虫算法的SVM(FA-SVM)和基于布谷鸟搜索算法的SVM(CS-SVM)作为对比实验，与GFCS-SVM相比较。

参数设置如下：SVM的惩罚因子C和核函数的参数σ上界为100，下界为0.01；PSO算法速度上界为5，下界为-5，学习因子γ1=γ2=1.5；FA算法步长因子k=0.5，光强吸收系数r=1，最大吸引度h=0.2；CS算法被发现概率Pa=0.25，步长因子a0=0.01；GFCS算法动态发现概率P∈[0.1,0.4]，自适应步长因子a0∈[0,0.02]，惯性权重w*∈[0,1]。PSO、FA、CS和GFCS算法的种群规模N=30，最大迭代次数T=200。

通过各个算法在6个UCI数据集上的实验仿真，分析GFCS-SVM分类性能。图5给出了GFCS算法优化SVM参数后在不同数据集分类效果，表4给出各算法在不同数据集上寻找的最优惩罚因子C和核函数的参数σ，表5给出各算法在不同数据集的分类准确率。结合图5和表5可以看出，GFCS-SVM在6个UCI数据集上都得到了最佳分类准确率。因此，和传统的SVM、原始群智能算法优化SVM相比，GFCS算法优化后SVM具有更好的分类效果。这是因为GFCS-SVM全局寻优和局部搜索最优解能力增强，可以更精确地锁定惩罚因子C和核函数的参数σ(见表4)，使得SVM分类准确率提高。

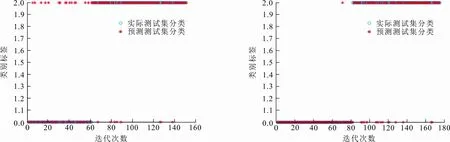
(a) Heart-c数据集 (b) Ionosphere数据集

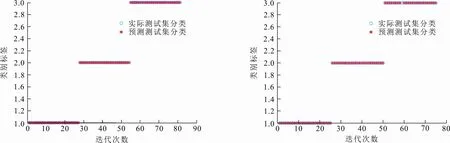
(c) Wine数据集 (d) Iris数据集

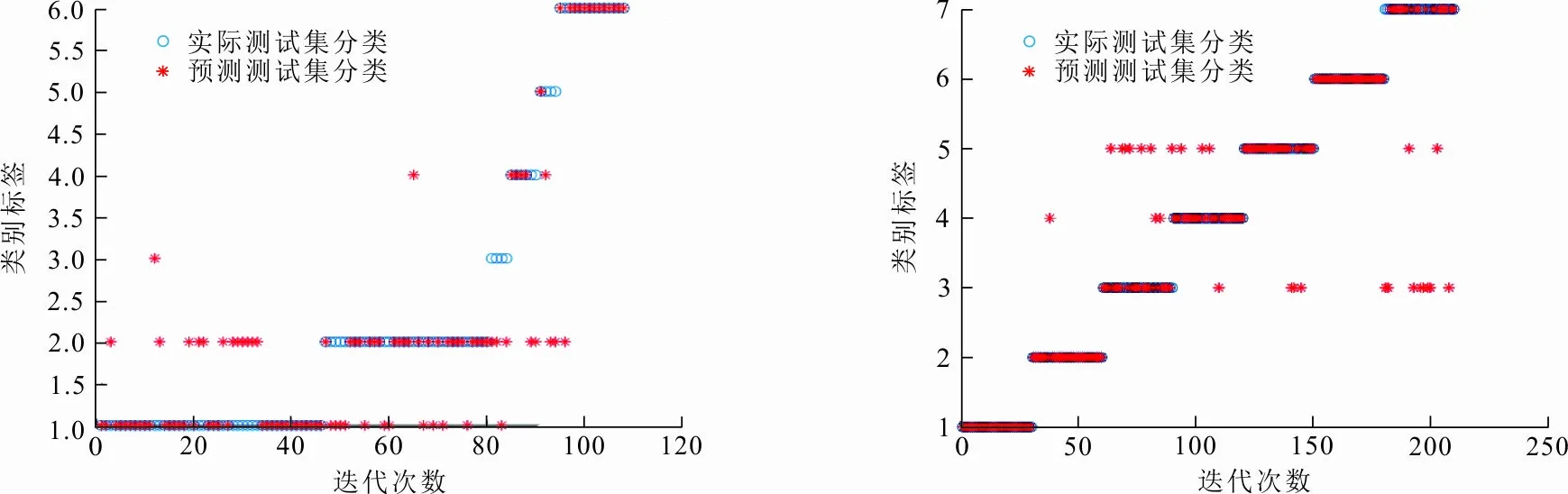
(e) Glass数据集 (f) Image-seg数据集图 5 GFCS-SVM在不同数据集的分类结果Fig.5 Classification result of GFCS-SVM on different data sets

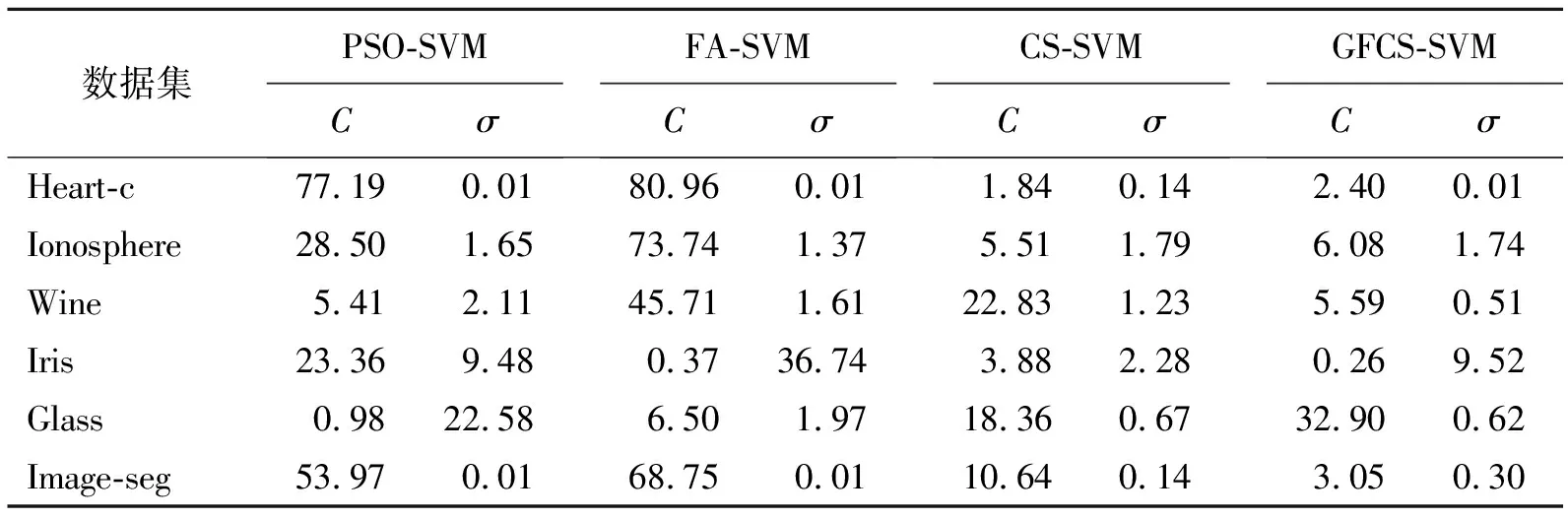
表 4 各算法在不同数据集上寻找的最优参数

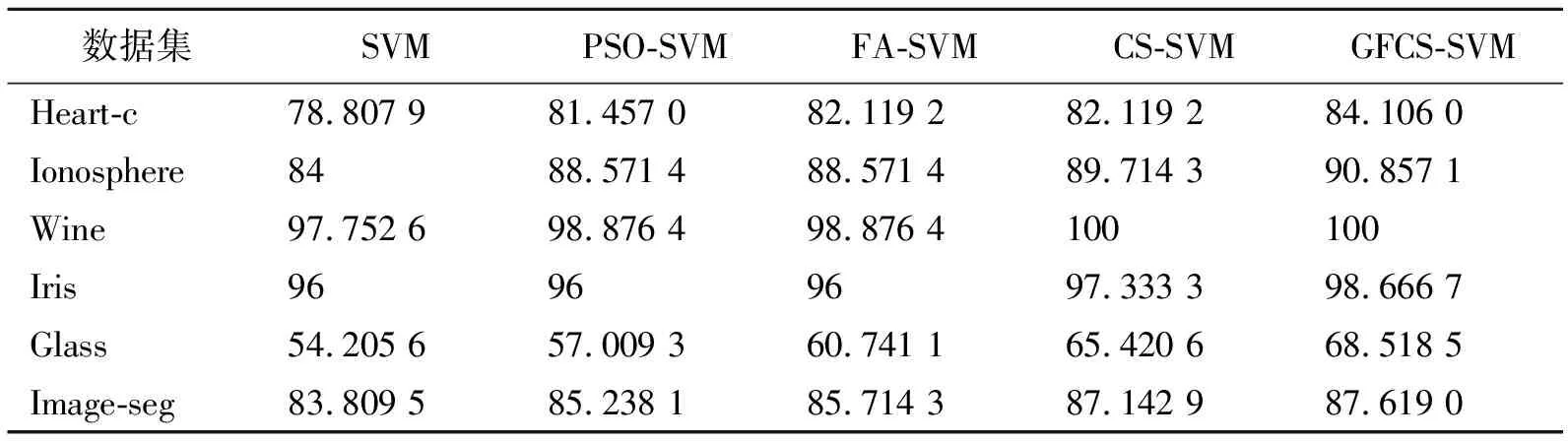
表 5 各算法在不同数据集上的分类准确率

5 结 语

针对原始布谷鸟搜索算法存在的易陷入局部最优、求解精度低,以及收敛速度慢等问题，从发现概率、步长因子和惯性权重等3个方面改进原始算法，提出了GFCS算法。通过6个基准测试函数的仿真，结果表明GFCS算法收敛速度快、有很强的稳定性和寻优能力。将GFCS算法应用于SVM惩罚因子C和核函数的参数σ寻优，避免了SVM参数选择盲目性；通过在6个UCI数据集进行测试，与未优化参数的SVM、PSO-SVM、FA-SVM、CS-SVM相比，GFCS-SVM分类效果最好。因此，GFCS算法是有效的SVM参数优化算法。未来可以将GFCS算法应用于其他SVM模型，如最小二乘支持向量机、孪生支持向量机和非平行超平面支持向量机等，解决大规模数据分类问题。