基于改进的Relief F多生理信号情绪识别算法

张晓丹,杜金祥,李 涛，佘翼翀，赵 瑞，柯熙政，康俊玮，王舒仪

(1.西安工程大学 电子信息学院，陕西 西安 710048；2.西安电子科技大学 生命科学技术学院，陕西 西安 710071；3.西安理工大学 自动化与信息工程学院，陕西 西安 710054)

0 引 言

21世纪被称为人工智能与脑科学的世纪[1]。情绪识别是通过获取人的生理和非生理信号对人的情绪状态进行自动辨别，更加友好和自然地实现人-机交互[2-3]。根据国际“10-20”系统分布在整个头皮上的16、32、64或128通道获取多通道脑电信号,电极数的增加会带来特征维数急剧上升，导致计算量过大，不利于特征情绪的分类[4-5]。文献[6]证明在进行情绪识别时，使用少数电极的数据并不影响识别准确率；文献[7]通过Relief F算法进行通道选择，选择16位被试者的通用最优通道；同理，因为被试者之间的个体差异，同样的特征并不能精确反应部分被试者的信息[8]；文献[9]利用F-score算法进行被试特征选择时，发现当特征数减少一半时，对应的情绪识别准确率基本保持不变；文献[10]在研究基于唯独模型的不同情绪识别准确率的评价方法中，利用Relief F算法进行了降维处理。根据“情绪效价假说”[11-13]，即大脑在处理消极和积极情绪时的前额非对称性，选取前额的对称电极,进行效价维度的两类情绪识别。为了综合考虑信号的时频域信息常采用小波分析[14-15];文献[16]使用小波能量矩进行脑电信号情绪识别，结合K近邻分类器分类准确率最高达到91.07%；文献[17]提取时域和频域特征，并使用K近邻进行唤醒度和效价二分类，平均识别准确率达到69.9%、71.2%；文献[18]通过脑电、肌电、皮肤电等外周生理信号进行情绪研究，采用最小二乘支持向量机进行识别；文献[19-20]使用K近邻算法进行音乐情感分类。

上述研究均存在因被试者个体特异性与全局阈值不匹配，以及仅采用单一脑电信号忽视了肌电、眼电中含有与情绪相关的信息而导致的正确率不高等问题。为解决以上问题，本文提出一种改进的Relief F匹配多生理信号特征选择方法。首先，通过优化特征组权重，获得不同被试者多生理信号特征组的权重，其中多生理信号包括脑电信号、肌电信号、眼电信号；其次，优选该被试者的匹配特征组，剔除冗余，同时根据特征组进行通道选择，减少特征维度；最后，采用概率神经网络(product-based neural network,PNN)和支持向量机进行识别验证算法的有效性。

1 数据处理与算法描述

1.1 数据来源与预处理

1.1.1 数据来源

在生理信号情绪分析数据库(database for emotion analysis using physiological singles，DEAP)[21]上进行实验测试。该数据库由Koelstra等人在2012年建立，包含32名被试者，每个被试者观看40段视频，被试者每观看1个视频被视为1个独立的实验。每个实验记录被试者的32通道的脑电信号和包含眼电、肌电等8通道的外周生理信号。视频观看结束后，被试者需使用自我评价模型分别在效价、唤醒度、优势度以及喜好程度4个维度进行打分。

1.1.2 数据预处理

首先，对32位被试者36通道生理信号去除3 s基线数据，剩下的60 s信号作为实验数据；其次，为了增加样本个数，使用8 s时间窗分割样本，相邻的时间窗有4 s的重叠窗，因此每个被试者对应40×14=560个样本；最后，采用“效价-唤醒度”情绪分类模型，对标签中的效价和唤醒度进行标准化处理，阈值为5，表1为情绪和标签所对应的关系。

表 1 情绪分类标签Tab.1 Emotion classification label

1.2 算法描述

1.2.1 传统Relief F算法

Relief F算法[22]是一种特征选择算法,即根据信号特征与分类标签的相关性给特征向量赋予权值,并根据权值大小删选对分类效果影响较小的特征子集。采用Relief F计算每类特征的权值，判断每类特征对分类的贡献度(即识别准确率)，其中需要计算各类特征的权重系数，式(1)为样本总量为m的样本集中第i个样本权值的计算公式。其权重系数变化，即

(1)

式中：W(fl)为权值集合，fl为第l个特征的权值;Hj为R与同类样本的间距;Mj(C)为R与不同类样本的间距;P(C)为C在样本集中所占比例;D(fl,R1,R2)为R1,R2两类样本在特征fl上的距离。当fl连续时，有

(2)

通过Relief F算法，将特征子集中全部特征权值相加，得到每类特征的权值并按其大小计算每类特征对分类的贡献，在进行情绪识别时需要使用多类特征进行组合作为分类的依据，但Relief F算法对消除冗余效果欠佳，因此，本文提出Relief F匹配多生理信号特征选择(relief F matching multi-physiological signal feature selection，RMMSFS)方法，通过Relief F算法计算特征种类和通道的权值，并通过使用交叉验证得到的分类贡献度对权值进行调整，剔除无关信息与冗余信息，得到识别使用的匹配特征组，提高识别准确率与减少运行时间。

1.2.2 RMMSFS方法

RMMSFS方法由特征种类选择和通道选择组成，利用特征种类选择得到被试者的所有特征的权值，并选出情绪识别率高的优选特征组，再根据特征的权值进行通道选择，有效地减少了通道数，提高了情绪识别率。

Ⅰ) 全局最优匹配特征组和通道选择。RMMSFS方法步骤:

步骤1：使用Relief F算法计算预处理后数据的n类特征权重。权值越大对正确分类的贡献越大；若权值为负值则相反。

步骤2：判断特征权重是否小于0，删除对分类有负作用的特征；将剩余特征组成优选特征组，重复使用Relief F算法，直到特征中没有负权值。

步骤3：将优选特征组中所有的特征进行降序排列，采用PNN分类器及20次5折交叉验证，得到前n类及n+1类特征识别准确率p(n)和p(n+1)。

步骤4：设定阈值δ1=0.01，判断|p(n+1)-p(n)|<δ1:

1) |p(n+1)-p(n)|<δ1，若前n+1与前n项的差绝对值小于阈值，则完成特征选择。

2) |p(n+1)-p(n)|>δ1，若大于阈值，则判断p(n)和p(n+1)的大小关系:

当p(n+1)>p(n)时，按式(3)计算前n项特征权值，获得更大增益。

(3)

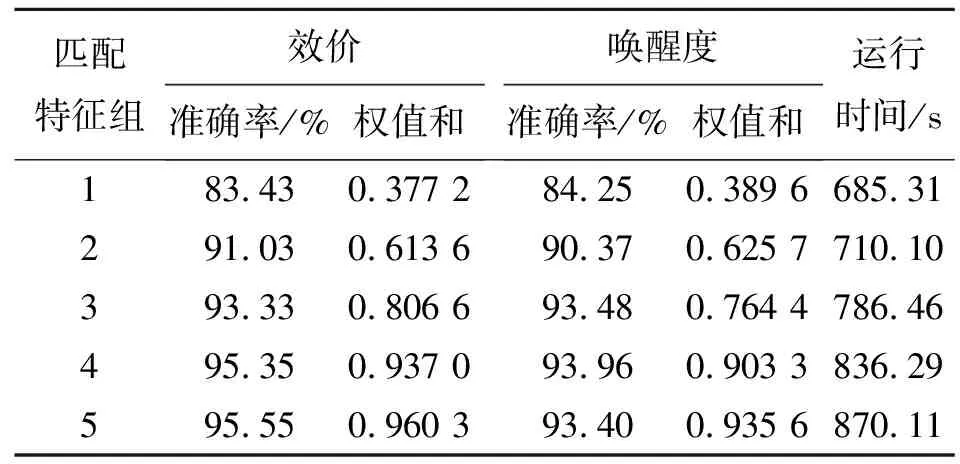
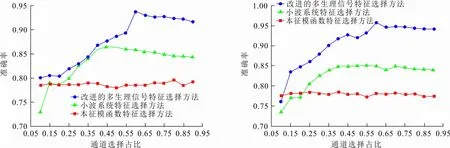
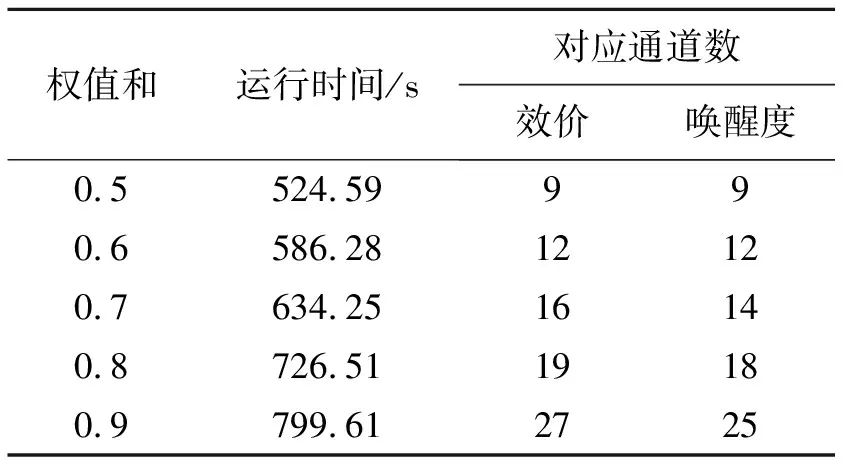
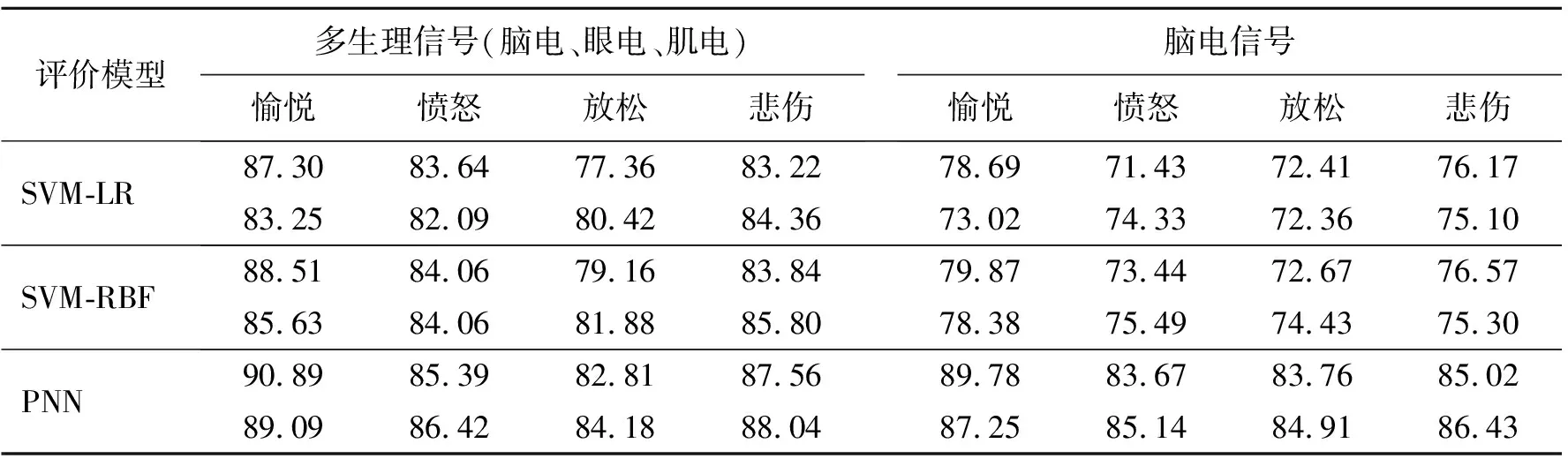
当p(n+1)

(4)

步骤5：使用优选特征组作为输入，计算36生理通道权重，并降序排列。

步骤6：剔除权重为负的生理通道，重复计算更新权重，直到所有生理通道权重为正。

步骤7：设定可变阈值δ2(δ2=0.05，0.1，…,0.9)，取权值和小于δ2的前n个通道，不同域值组成多种生理通道组合。

步骤8：通过PNN分类器进行20次5折交叉验证,得到不同通道组合的识别准确率及运行时间，最终输出最优通道优选特征组。

Ⅱ) 优化特征权重因子。通过Relief F算法，将特征子集中全部特征权值相加，得到每类特征的权值并按其大小计算每类特征对分类的贡献，但进行情绪识别时，需要使用多类特征进行组合作为分类的依据，且消除冗余的效果欠佳。区别于传统Relief F算法，本文使用权值在匹配特征组中所占比例对特征每个权值统一调整，使权值较大的特征得到更多的增益，而权值较小的特征得到较小的增益，这样可以使对分类贡献较高的特征在特征组中占有更重要的作用。在步骤4的式(3)中，更新特征权重排序，重新分类判断p(n)和p(n+1)的大小关系，一直更新权重直到满足阈值条件，此时完成前n类的特征选择。

1.2.3 PNN

PNN是一种结构简单的人工神经网络模型，分别为输入层、模式层、求和层以及输出层4个网络层次，PNN网络结构拓扑图如图1所示。

图 1 PNN网络结构拓扑图Fig.1 PNN structure topology of network

PNN样本层将输入的脑电、眼电和肌电信号进行加权，通过激活函数传输到PNN求和层，即

(5)

式中：ci为径向基函数中心值;δi为特性函数第i个分量所对的阈值参考量值。PNN利用非参数估计法求和估计各类的概率,即

(6)

式中：X为需要识别的样本数据；CI为标签的类型；m为数据向量的维度信息；δ为平滑参数；n为第i类别的样本数量。

2 结果与分析

本文所提算法在Matlab2017b软件上进行实验，硬件平台CPU为intel(R)Core(TM)i5-7400，主频为3 GHZ，机带RAM为8 GiB，搭载Windows10,64位操作系统。

2.1 单被试者特征选择

选用DEAP中的第25位被试者作为实验对象，通过对数据预处理，将560个样本按效价和唤醒度标签随机分为2组，取各自1/2样本为训练集，剩余部分为测试集。第25位被试者的特征类别选择结果见表2。

表 2 特征类别选择结果Tab.2 Results of feature category selection

从表2可以看出：随着特征种类增多，权值与分类准确率增大，当超过4种特征时识别准确率无明显变化，而程序运行时间明显增加。基于前4种特征的效价二分类准确率为95.35%，相较于前3类特征识别准确率增加0.020 2，大于设定阈值δ，随着特征数量的增加，正确率增量绝对值均小于δ，故该被试者效价二分类的匹配特征组为其优选特征组的前4项特征；基于前4项特征的唤醒度二分类准确率为93.96%，前3项特征组分类准确率为93.48%，二者差值为0.048，小于阈值δ，故唤醒度二分类的匹配特征组为其优选特征组的前三项特征。

由于被试者之间存在个体差异性，不同被试者匹配特征组不尽相同，而且不同特征直接影响相应通道权值的大小，从而影响识别结果，因此针对不同被试者选择匹配该被试者的特征组是正确识别情绪的重要前提。第25名被试者效价和唤醒度二分类通道选择结果如图2～3所示。

图 2 效价二分类通道选择结果 图 3 唤醒度二分类通道选择结果 Fig.2 Results of potency binary classification Fig.3 Results of potency binary classification channel selection channel selection

从图2～3可以看出，3条曲线分别为使用RMMSFS方法、小波系数特征与本征模函数分量特征通道选择准确率曲线，体现了在通道选择过程中不同方法的准确率变化规律,通道权值不同时各自对应的前n个通道的识别程序的运行时间见表3。

表 3 通道不同权值时程序运行时间Tab.3 Run time of program when channel selects different weights

从表3可见看出，采用RMMSFS方法进行特征选择的识别正确率随着选择通道权重和的增加而增加，当通道权值和为0.60时，2组分类结果都达到了最大值，分别为95.46%和93.63%，对应表3使用的通道个数均为12个，识别程序运行时间为586.28 s，较未经过通道选择时的836.29 s缩短了42.64%；当通道权重和为0.9时，随着通道权重和的增加，识别正确率并未显著增加，效价和唤醒度的通道数分别为27和25，所耗时间增加至799.61 s。表明特征数增加到一定数量时，对应的通道数也随之增多，数据冗杂反而影响情绪平均识别率。因此，综合考虑准确率与时间复杂度，在效价和唤醒度二分类时选择权重和为0.6时对应的通道。

2.2 RMMSFS特征选择

选用DEAP中32位被试者为实验对象，为增加样本容量，取4 s重叠时间窗将时长60 s的样本划分为14段，每段对应1 024个数据点，分为2组，进行100次随机实验。全体被试者效价和唤醒度二分类的匹配特征组构成及其权值如图4～5所示。

图 4 效价二分类匹配特征组构成及其权值Fig.4 Composition and weight of valence binary matching feature group

图 5 唤醒度二分类匹配特征组构成及其权值Fig.5 Composition and weight of arousal binary classification matching feature set

由小波系数均值、小波系数标准差、本征函数分量标准差与小波能量4类特征中的2～4类特征构成，但不同个体之间的匹配特征组构成有较大的差异：有32.81%样本的匹配特征组含有4类特征，59.38%样本中含有3种特征,而仅有7.81%被试者分类结果明显受2种特征影响。而第13位被试者的唤醒度二分类的匹配特征组由小波能量与本征函数分量标准差构成，且未经过RMMSFS特征选择的权值为负，说明其对大部分样本的分类有消极影响，而仅在该位被试者的唤醒度二分类中起到较强的积极作用，如图5中红色虚线框内所示。由此可知，此4类匹配特征及其权值虽然对大部分被试者适用，但不能匹配所有被试者。同时，若样本比例增加，匹配特征特异比例将会进一步上升。

2.3 PNN识别结果

对DEAP数据集32位被试者利用RMMSFS方法分别识别脑电和多生理信号在PNN模型下的4类情绪。对于每一位被试者，从脑电、眼电和肌电中组成的多生理信号中的每类情绪的特征样本中抽取一半样本作为训练集，剩余样本作为测试集，通过PNN分类器获得最终多生理信号分类结果。首先，在RMMSFS多生理信号特征提取算法中，计算每一类特征的权值并按降序排列，剔除权值为负的特征。选择不同特征及其对应通道的权值(贡献度)，根据贡献度调整其权值及其对应通道、多生理信号和脑电信号前n个特征对应的平均识别准确率见表4。

当脑电信号的特征数为21时，所需平均通道数为11.13，是多生理信号组合特征算法的2倍，且57.58%的识别率低于多生理信号组合特征62.72%；当脑电信号特征提取最高平均识别率为85.55%时，平均通道数为22.05，特征数为85个，多生理识别准确率最高达到87.31%,高于脑电通道1.76%，所需的通道数也少于脑电信号。当特征数增加到90以后，脑电信号平均识别率明显低于多生理信号的识别率，且呈现急速下降的形式。表明特征数增加到一定数量时，对应的通道数也随之增多，数据冗杂反而影响情绪的平均识别率。

表 4 多生理信号和脑电信号前n个特征对应的平均识别准确率Tab.4 Average recognition accuracy corresponding tothe first n features of multiple physiologicalsignals and EEG signals

2.4 算法与情绪识别结果

2.4.1 RMMSFS方法与Relief F算法对比

为了验证RMMSFS算法的有效性，对DEAP数据库32位被试者进行效价和唤醒度分析，使用传统的Relief F算法选择不同的2组特征，分别使用其中小波系数特征和小波能量熵、重构信号本征函数分量差值，使用PNN进行识别。其中RMMSFS代表改进的Relief F匹配多生理信号特征选择算法，Relief F COE代表使用小波系数特征进行实验，Relief F IMF代表使用重构信号本征函数分量差值进行实验。3组实验4分类情绪识别以及平均分类结果见表5。

表 5 情绪四分类实验结果Tab.5 Experimental results of four emotion classifications 单位：%

从表5可以看出，愉悦情绪识别率最高为90.89%，对比Relief F COE组提升7.50%，对比Relief F IMF组提升27.62%。而在放松情绪识别率最低为82.81%，对比Relief F COE组提升3.97%，对比Relief F IMF组提升28.33%。总体4类情绪的识别率皆高于82%，其中，4类情绪的平均识别率达到87.30%，而在Relief F COE情绪4分类中平均识别率为80.95%，Relief F IMF4分类平均识别准确率为60.17%，由此可见，使用RMMSFS方法可有效提取多生理信号中与情绪相关性较强的特征，优于传统的Relief F算法。

2.4.2 PNN与SVM情绪识别结果对比

为了验证PNN识别算法的有效性，采用PNN和SVM不同核函数分别进行多生理信号和脑电信号4分类情绪识别，并对2种分类模型进行综合评估。PNN和SVM不同核函数情绪识别结果的数据对比见表6。从表6可以看出，首先从脑电信号与多生理信号分析PNN与SVM不同核函数4类情绪的识别率和外周生理信号均得到提升，PNN平均提升1.76%，SVM平均提升8.28%，更加验证了多生理信号包含的情绪特征更利于情绪识别。其次，模型方面采用PNN多生理信号特征下的情绪分类准确率较SVM不同核函数的分类准确率都有一定程度的提高。RBF核函数准确率和F1值均高于LR核函数，是因为选择的数据特征数量较小，样本数量一般，后续选用RBF核函数与PNN对比。PNN对比RBF核函数的悲伤情绪识别准确率提升了3.72%，愤怒情绪最低提升了1.33%，4类情绪平均提升了2.07%。再次，其他指标如评价召回率与精度常采用更客观的F1值来综合评价，F1值越高，代表该模型的性能越好。从整体来看，2种模型在识别4类情绪时F1值都大于80%，其中PNN识别愉悦、愤怒、放松、悲伤的F1值分别为89.09%、86.42%、84.18%、88.04%，对比SVM分别提高了3.36%、2.36%、2.30%、2.24%。因为不同情绪状态下的脑部活动及反应并不是一种简单的线性系统，若把不同的脑电情绪特征进行简单的线性组合时，容易破坏脑电情绪特征的原本的非线性结构，使不同的情绪特征之间出现负面作用，进而导致了特征冗余的增加，背离了充分利用多生理情绪特征的初衷。因此本文的方法，能使脑电、眼电和肌电生理信号的情绪特征有效地组合在一起，提升了情绪识别的分类性能，证明本文提出的基于RMMSFS方法与PNN组合方式能够较充分挖掘生理信号的情绪信息。

表 6 PNN与SVM情绪识别准确率

3 结 论

1) 优化权重公式，获得特征组的分类贡献度和被试者匹配特征组，以及在匹配特征组中所占的比例，优选出有效的匹配特征组，剔除贡献度小的特征组，提高了算法识别准确率和效率。

2) 有效地识别不同被试者的特异性特征组，并根据被试者特异性特征选择通道，获得更高的识别准确率。

3) PNN与传统SVM算法进行对比，在4类情绪识别中均能够获得更高的识别准确率。RMMSFS方法能够获得全局匹配特征组和不同被试者的匹配特征组，提高了识别准确率和算法效率，验证了RMMSFS方法的有效性与可行性。