既有桥梁结构承载力检测及评估研究

郑宗鹤 樊聪镐

（中国市政工程中南设计研究总院有限公司，湖北 武汉 430014）

既有桥梁在运营期间，往往会出现一定程度的性能损失，使得其承载能力持续下降。尤其是在我国基础工程建设数量与体量飞速发展的背景下，桥梁监测的要求也越来越高。通过可靠的结构承载力检测与评估，能够较为准确地判定结构的损伤情况以及预期寿命，进而为后续结构的改建、加固等提供相应的理论支持。目前我国在桥梁结构承载力检测方面所应用的技术较为繁多，其中荷载试验凭借简单、有效的优势得到了广泛的应用。荷载试验不仅能够在新建工程中发挥良好的作用，同时也可用于旧桥加固前的检测评估。其中，对于新建桥梁而言，荷载试验能够较为准确、直观地反应结构的质量好坏，一般而言在重大桥梁工程项目正式投入运营前都应当通过荷载试验来做出评估；而对于旧桥而言，荷载试验能够针对性地提出加固指导意见，并为加固后结构的维护建立参考。

1 工程概况

本文以我国某桥梁工程实例为基础展开分析，该项目采用预应力混凝土连续梁桥设计，共四跨（33m+45m+45m+33m）。桥面分为左右幅，选定为双向六车道方案。设计荷载定为公路- Ⅰ级，设计车速为50km/h。该项目各跨的布置如图1 所示，目前已竣工投入运营达5 年。

图1 桥跨布置情况

2 有限元模型构建

本文采用Midas/Civil 软件建立与工程结构相应的模型并完成有限元分析。在本模型中，共将结构划分为79个节点及78 个单元。其中主梁的材料定义为C50 混凝土，其中的纵向预应力筋定义为15.24 钢绞线（fpk=1860MPa），预应力筋在张拉时应当将张拉应力控制在1395MPa 附近，且均以端部张拉的方式完成。由此所建立的有限元模型如图2 所示，各支座的约束条件如表1 所示。

图2 有限元计算模型

表1 各支座约束条件

3 承载力试验分析

3.1 静载力试验

3.1.1 试验工况

基于桥梁结构特点及其受力性质，可将静力荷载大致分为两个不同工况条件，并分别测试其最大正弯矩及最大负弯矩，荷载试验检测工况表如表2 所示。

表2 静载试验工况表

通过荷载试验测试可以得到控制截面弯矩的影响线如图3 和图4 所示。

图3 10-11#轴跨中最大正弯矩影响线

图4 10#轴最大负弯矩影响线

3.1.2 静载试验结果分析

控制截面的应力测试结果。通过静载试验结果发现，工况一、工况二在各级荷载下的应变、卸载时的应变以及相对残余应变分别如表3、表4 所示。表中数值为正则代表拉应变，负值则代表压应变。根据表中数据可以发现，试验荷载下结构出现的最大、最小残余应变比分别为18%、0，两者均满足我国现行规范20%的限值标准。

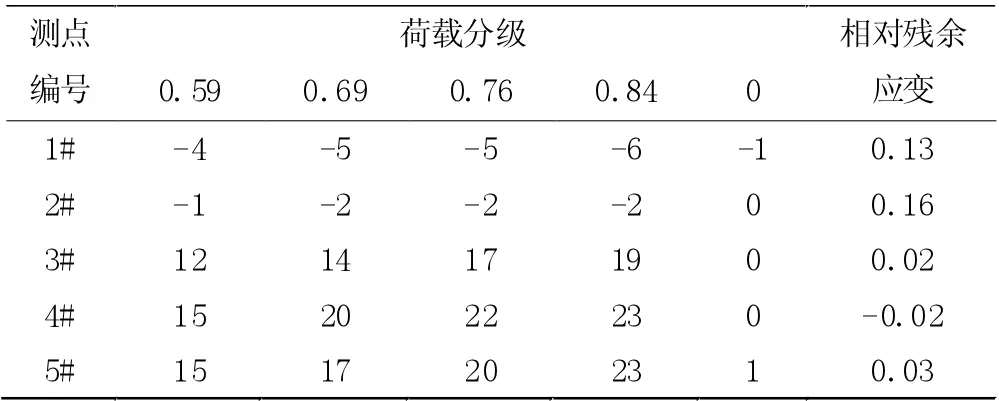
表3 工况一应变实测结果（部分）

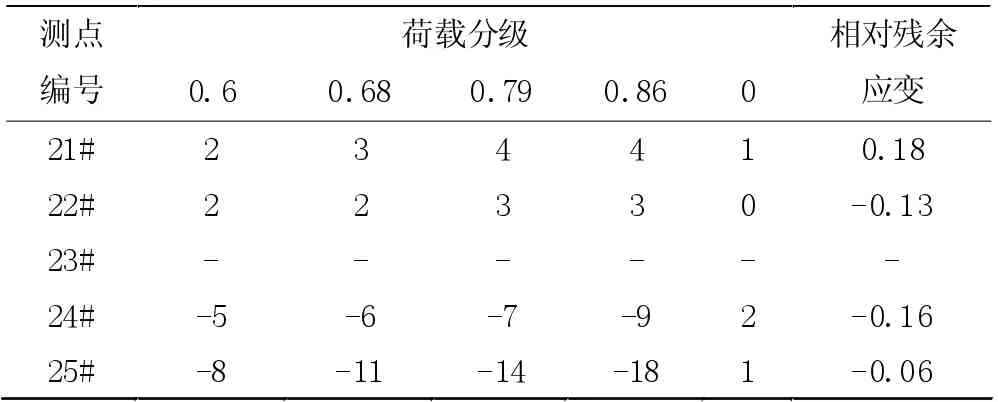
表4 工况二应变实测结果（部分）

试验研究发现，对于边梁不同侧面的相同高度位置，试验实测得到的应变量往往存在突出的差异，且受拉挖侧的应变显著大于内侧；但在受压区则呈现出相反的规律，这也表明梁体自身具有一定的斜弯曲。在结构中设置各个测点的实测数据与弯矩值之间保持近似线形相关，因此可以认定在该阶段下截面处于线弹性状态，由此也可得到在试验荷载作用下结构产生的最大应变。此外，试验实测得到的应变值与截面高度之间存在线性关联性，因此在试验过程中截面满足平截面假定。

按照上述研究结果即可归纳得到应变的回归方程，并以此为基础进一步推断得到最大试验荷载下的平均拉应变及平均压应变。在结构处于完全线弹性状态下时，可以通过测定测点处的应变情况来大致推算得到该位置的应力水平。其中计算值、实测值之间偏差可以通过结构效验系数来反映。对预应力混凝土桥而言，我国现行规范要求应当将这一指标控制在0.6-0.9 的区间内。调取有限元分析中工况一、工况二下控制截面的边缘应力水平，将其与试验实测值比对即可得到表5。

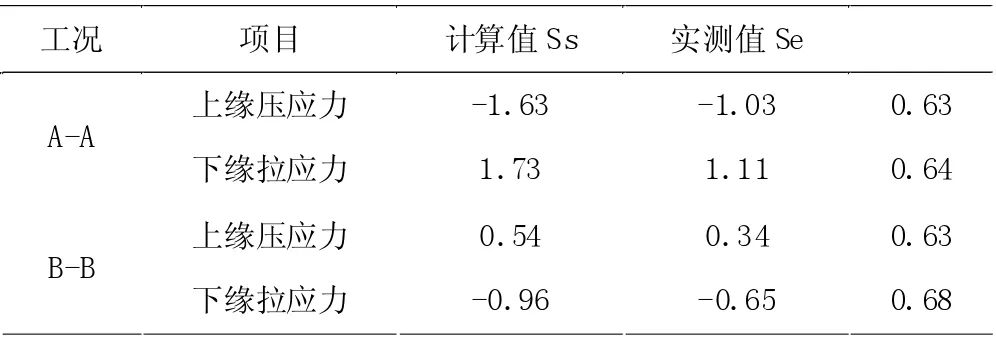
表5 实测值和计算值对比分析表

3.1.3 抗裂性分析

在预应力混凝桥梁的结构管理中，抗裂性也是一项需要重点关注的内容，同时其也直接反映着结构整体的承载能力。在开展荷载试验时，应当优先选用跨中位置顶部约1m 的区段，在其上连续布设5 个应变传感器，以此获取该位置在不同等级荷载所发生的应变。将荷载效率系数、实测应变分别作为X 轴、Y 轴，即可绘制得到ε-ηq 图，若在图中曲线存在拐点，也即代表在该试验测点位置出现开裂。

试验表明，实测应变、外加弯矩之前保持着较好的线性关联性，这也代表在加载过程中结构并未产生开裂现象。此外，试验加载时技术人员也对结构进行了全面的观察，并未发现裂缝，因此可认为梁体具有较好的抗裂性能。

3.2 动载力试验

3.2.1 行车试验

监测行车试验开展全过程中跨中以及1/4 跨位置处的振幅和动位移指标，并将其分别列在表6 及表7 中。

表6 行车时各测点响应幅值(mm)

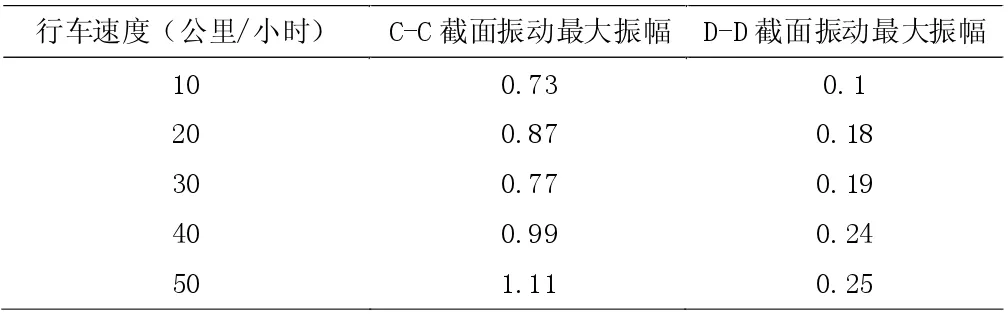
表7 行车时各测点响应幅值和冲击系数

根据研究结果可以发现，跨中及1/4 跨位置处的最大振动幅值均在500km/h 时达到，且这峰值随着车速的增加呈现出增加的趋势。同时，冲击系数与车速之间也存在正相关联，车速越大、冲击系数越大，当车速达到30km/h 时，试验测得相应的冲击系数为0.19，这与设计值比较贴合。

通过行车试验数据的自谱分析可以发现，在外加车辆荷载的基础上桥梁结构的自振频率分别达到了2.64Hz、3.51Hz、4.64Hz 以及5.08Hz。

3.2.2 制动试验

在试验过程中，借助自重为38 吨的车辆在跨中处开展两次制动。在跨中及1/4 跨位置处分别布置一个测点，测量桥梁顺桥向的振动响应，测得振动幅值如表8 所示。

表8 制动试验中跨中纵向振幅(单峰mm)

通过分析可以发现，制动试验中结构振动的衰减频率约为2.54Hz、3.66Hz 及5.08Hz。

3.2.3 跳车试验

在试验过程中，借助自重为38 吨的车辆在跨中处开展两次跳车试验，保持车辆顺下坡方向前进。在跨中及1/4 跨位置处分别布置一个测点，测量桥梁结构内产生的相应，其数据如表9 所示。

表9 跳车引起的最大振幅(单峰mm)

针对跨中位置的跳车余振做出分析发现，结构振动的衰减的频率约为2.59Hz、3.61Hz、4.64Hz 及5.08Hz。

3.2.4 脉动试验

受到风荷载、水流冲击等的影响，桥梁结构不可避免地会发生振动，在实际工程中可借助高精度设备监测结构振动情况，并以此为基础计算得到自振周期、振型、阻尼比等基本参数。传在本研究中将传感器布置于跨中及1/4 跨位置处，并分别获得相应的实测数据。在此基础上对脉动试验的结果展开研究发现结构的自振频率为2.62Hz、3.52Hz、4.57Hz 及5.08Hz。

3.2.5 桥梁固有频率理论值

在对桥梁结构开展自由振动分析时，若涉及到有限单元软件，一般可借助程序内置的子空间迭代法、多重Ritz 向量法等特征值计算法完成分析。其中，子空间迭代法对于大型矩阵特征值的求解具有较好的效果，在动力学研究中得到了广泛应用。系统整体一般具有较多的自由度，因此在分析其响应时仅要求掌握部分较低特征值即可，具有较高的求解效率。

在应用子空间迭代法进行求解时，需要首先假定r个起始向量并对其进行迭代计算以此得出矩阵的前p个特征值及其相应特征向量。若r 较小，不仅可能导致遗漏振型，同时还可能得出原不应出现的振型。

在通过有限元分析即可得出该桥梁结构固有频率的前5 阶计算值，如表10 所示。

表10 桥梁竖向固有频率理论计算值

根据表10 内容可以发现，该桥梁结构的横向、竖向一阶振动频率分别为1.05Hz、1.96Hz，且竖向一阶振动频率出现的时间稍晚，这表明结构在竖向上的刚度要大于横向，这与工程实际设计方案中的结构体系相契合。试验实测得到的自振频率均高于理论分析值，这也表明结构是刚度较理论更大，但仍处在合理范围内。

4 承载力评估分析

4.1 基于静载试验的承载力评估

4.1.1 应力校验系数

在工况一条件下测得上缘、下缘的压应力校验系数分别为0.63、0.64；在工况二条件下测得上缘、下缘的压应力校验系数分别为0.63、0.68。实测数据均满足我国现行规范的0.6-0.9 区间要求，且较标准区间更小，这也表明结构的应力状态较好。

4.1.2 挠度校验系数

在工况一条件下测得挠度校验系数为0.71，满足我国现行规范的0.7-1.0 区间要求，且较标准区间更小，这也表明结构的刚度较好。此外，将截面最大挠度控制在合理范围内，使得设计挠度小于L/600，这也满足我国现行规范的刚度要求。

4.2 基于动载试验的承载力评估

4.2.1 自振频率

根据理论分析得到该桥梁结构的一阶自振频率为1.05Hz，而在行车试验、制动试验、跳车试验以及脉动试验下分别实测得到结构的一阶自振频率为2.64Hz、2.54Hz、2.59Hz 以及2.62Hz。由此可见发现，实测得到的自振频率均大于理论分析值，这也表明结构实际刚度较大，这与静载试验的分析结果较为契合。

4.2.2 冲击系数

随着车速的提升，冲击系数也随之逐渐增大。当车速达到30km/h 时，其所对应的冲击系数实测值则为0.19。冲击系数较标准值更高，这就表明桥面平整度较差，在日常维护运营中应当采取有效措施进行改善，降低冲击效应的不利影响。

5 结论

本文基于目前国内外常见的桥梁承载力评价方法，分别从静载试验、动载试验两个层面展开分析，结合我国某四跨连续桥工程实例比对了Midas/Civil 有限元分析与试验实测数据。研究发现，桥梁结构所发生的变形均符合我国现行规范要求，且结构实测得到的残余挠度较小，受力过程中结构始终处于线弹性状态下。此外，动载试验测得结构的实际自振频率较理论分析值更大，反映了结构具有较高的刚度这与静载试验的结果较为一致。