分数阶MAC 系统同步及其在保密通信中的应用

李贤丽，温玉玉，朱金元，汤俊杰

（东北石油大学物理与电子工程学院，黑龙江大庆 163318）

近几年来，随着分数阶系统表现出丰富的动力学性质，混沌理论的研究及应用在很多领域都引起了极大的关注。研究者发现了很多分数阶混沌系统，如Duffing振子[1-2]、chua系统[3-5]、Liu 系统等[6-7]。为了丰富和发展分数阶混沌研究，也基于混沌在现实中的应用，关于系统的同步控制以及在保密通信中的研究等逐步引起了大家的关注。

十九世纪末，Pecora 与Carroll 首次实现了混沌系统的同步，从此研究者们开始对混沌同步展开了深入的探索，并且出现了很多同步方式和同步方法，如完全同步[8-9]、滑膜同步[10-11]、自适应同步[12]、主从同步[13-14]、投影同步[15-16]等。这些方法与方式适用于整数阶混沌系统的同时，对分数阶系统仍然适用，且生活中大多实际模型都是分数阶系统，因此，对分数阶系统作进一步的研究是有必要的。

文中对分数阶MAC 系统的混沌同步进行了探索和研究，并且将其应用在通信数据的保密传输中。基于李雅普诺夫直接法对系统进行了混沌同步，实现了系统的同步控制[17]，基于线性系统稳定性定理[18]，成功实现了信号的加密与解密。

1 分数阶MAC混沌系统

L.O.Chua 等提出了双涡卷MAC 系统，该系统的分数阶状态方程如下:

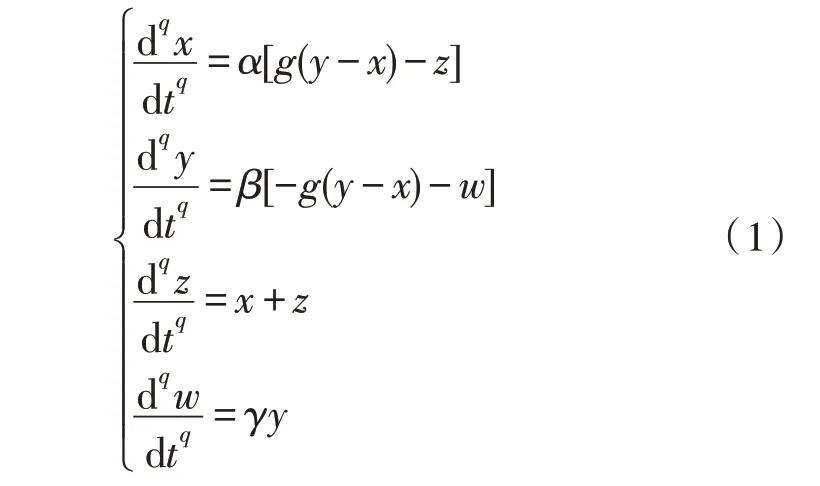
式中，x、y、z、w是系统的状态变量，q为系统分数阶导数的阶数，g(y-x)=m1(y-x)+0.5(m0-m1)[|y-x+x1|- |y-x-x1|]为3 个分段线性奇函数，α=2、β=20、γ=1.5、m0=-0.2、m1=3，x1是转折点，可为任意值，选取x1=0.5，在该取值下，利用预估-校正算法计算出分数阶MAC 系统随分数阶导数的阶数q变化的分岔图，如图1 所示。

图1 系统随阶数q 变化的分岔图

从图1 可以得出当阶数q∈[0.93,1)时，系统处于混沌状态。

图2 为阶数q取0.95 时的混沌吸引子。

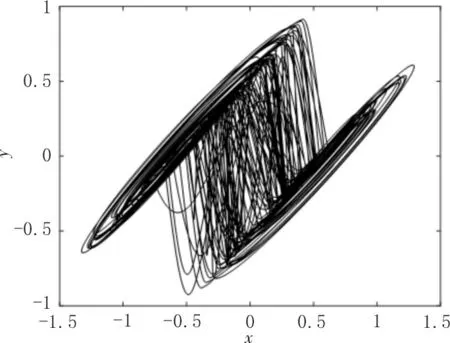
图2 阶数q=0.95时的混沌吸引子

2 分数阶系统的混沌同步

2.1 同步控制原理

若两个n维分数阶系统如下：

其中，x=(x1,x2,…,xn)∈Rn,y=(y1,y2,…,yn)∈Rn，u为系统同步设计的控制器。式（2）为驱动系统，式（3）为响应系统。定义误差为：

要使驱动系统和响应系统达到同步，则需设计合适的控制器，使x(0)和y(0)在任意初始状态都满足下列条件，即：

其中，‖ ‖· 为Rn中的范数，则系统的同步研究就转化为对系统误差的分析。该文采用李雅普诺夫直接法构造出一个能量函数V，通过计算V对时间的全导数来判断系统是否达到稳定状态。选择李雅普诺夫函数，计算该函数对时间的全导，若对误差方程的解为负定的，则误差系统在原点渐进稳定，即=0,i=1,2,…,n。故需选择合适的控制器u使对误差函数的解负定，从而使两系统达到同步。

2.2 控制器的选择

取式（1）作为驱动系统，响应系统如下：

2.3 同步数值仿真

利用预估-校正算法，对误差系统进行Matlab数值仿真，设定驱动系统（1）的初始值为x(0)=0.2、y(0)=0.2、z(0)=0.2、w(0)=0.1，响应系统（6）的初始值为X(0)=5、Y(0)=6、Z(0)=4、W(0)=6，阶数q=0.95。经过Matlab 软件仿真，同步误差曲线如图3 所示。

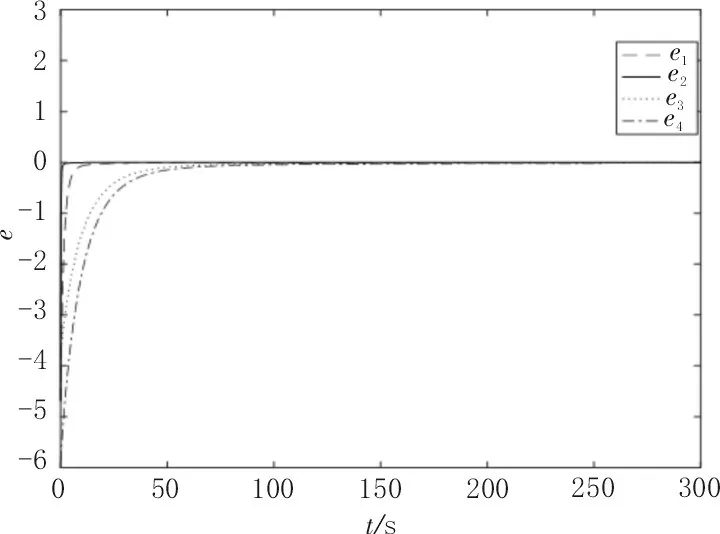
图3 系统（1）与（6）的同步误差曲线

由图可以看出，两系统的同步误差随时间t的变化逐渐趋于零，且在同步过程中非常平滑，没有反复震荡的现象，表明驱动响应系统趋于同步状态。

3 系统同步在保密通信中的应用

3.1 基于线性系统稳定性的混沌遮掩方案

考虑如下混沌系统：

再次构造一个新的系统作为响应系统：

其中，y=(y1,y2,…,yn)∈Rn，定义两系统的同步误差为e(t)=x(t)-y(t)，其解如下：

从式（13）可以得出，当矩阵A具有实部为负的特征值时，两系统即可达到完全同步。

基于上述同步方法对消息信号进行混沌掩盖，将要传输的消息信号i(t) 直接加到h(x(t))中的某一项，得到混沌信号与消息信号的叠加信号s(t)，混沌信号与数据信号经过混合传输到接收端。此时，输出端输出的信号即为同步后的混合信号h(y(t))，由于混沌系统已达到同步，所以在输出信号减去原混沌信号即可恢复出数据信号。

接收端的混沌响应系统如下：

利用接收端的混沌信号减去h(x(t))，得到解密后的消息信号为：

根据上述分析，该方法能够实现信号的加密和解密，也就实现了利用混沌信号对消息信号进行保密的目的。

3.2 数值仿真

将分数阶MAC 系统写成如下形式：

可以得到，当矩阵A具有实部为负的特征值时，两系统即可达到完全同步，从而能够成功恢复出消息信号。在数值仿真中，选取系统（17）和（18）的初始值为（0.2,0,0.1,0.1）和（1,2,1,3），图4(a)为需要加密的消息信号，图4(b)为消息信号与混沌信号叠加的掩盖信号，图4(c)为接收端恢复出来的消息信号，图4(d)计算出了该信号与原始信号的误差曲线图，从图中可以看出，在很短时间内，消息信号能够成功恢复出来。

图4 消息信号的加密与解密波形图

4 结论

该文对分数阶MAC 混沌系统进行了数值分析与计算，用Matlab 软件仿真出了系统随阶数变化的分岔图，从图中可以得出系统在各个阶数范围下的运动状态。用李雅普诺夫直接法实现了系统的同步控制[19-20]，从仿真出的误差结果可以看出，驱动响应系统误差值随时间的变化趋于零，表明系统已达到同步。最后，通过同步控制实现了保密通信，经过数值仿真得到了数据信号的波形图，并且绘制出原数据信号和恢复信号的误差图，经过短暂同步时间后，误差逐渐趋于零，成功实现了信号的加密与解密。