具有非线性记忆项的半线性Moore-Gibson-Thompson方程解的爆破研究
欧阳柏平, 侯春娟
(广州华商学院数据科学学院, 广州 511300)
在物理背景下,Moore-Gibson-Thompson(MGT)方程是描述在粘性热松弛流体中波的传播的数学模型,其数学表示如下:
τuttt+utt-c2Δu-bΔut=0,
其中,未知标量函数u=u(t,x)表示势函数,c表示声速,τ为热松弛因子,b=βc2与声音的扩散相关,τ(0,β]。需要说明的是,当0<τ<β时,其半群的指数是稳定的,而τ=β时,其半群的指数稳定性消失。
学者们对MGT方程解的存在性、爆破以及衰减等性态问题进行了研究[1-5]。如,文献[1]利用迭代方法结合切片技巧,研究了如下非线性项的MGT方程在次临界和临界情况下解的爆破问题:
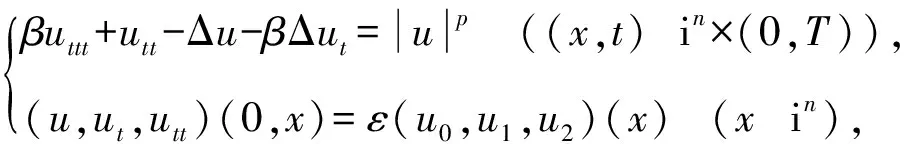
(1)
其中,p>1,β、ε>0,Δ是拉普拉斯算子。
文献[2]运用迭代等技巧,研究了β=0时的非线性记忆项的波动方程在次临界和临界情况下解的爆破问题:
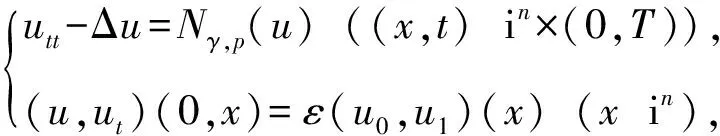
(2)
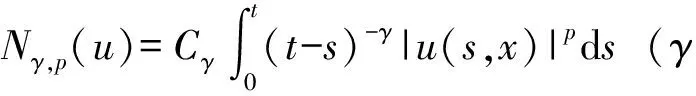
众所周知,有关波动方程柯西问题解的全局存在性与非存在性研究中,临界指数Pstr(n)(Strauss 指数)起着关键作用。方程(2)的临界指数Pstr(n,γ)由以下一元二次方程的正根表示:
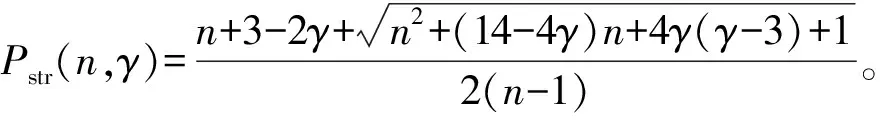
当n=1时,Pstr(1,γ)=∞。
已有研究主要利用Kato引理研究二阶波动方程解的爆破问题,然而,Kato引理只适用于二阶的波动方程,不适用于三阶的波动方程。近年来,有学者利用迭代技巧考虑了某些双曲方程解的爆破问题[6-10]。如,文献[6]利用迭代和泛函分析方法,研究了一般非线性记忆项下一类弱耦合半线性波动方程在次临界情况下解的爆破问题:
其中,p、q>1,gi(t)>0(i=1,2)。
文献[9]运用迭代技巧结合测试函数方法,研究了导数型非线性项下一类半线性双波动方程在次临界情况下解的全局非存在性问题:
其中,p>1,ε>0。
本文讨论具有非线性记忆项的半线性MGT方程解的爆破问题:
(3)

本文主要探讨非线性记忆项对半线性MGT方程爆破解的非局部影响。方程(3)中高阶扰动项βuttt-βΔut使得其迭代框架存在无界乘子,若运用文献[8-10]的处理方法,则在迭代过程中必然出现关于时间的指数形式衰减,仅能获得大初值下解的爆破,无法得到小初值下解的爆破。而对于半线性波动方程爆破问题的研究,小初值的爆破是其重点和难点。本文通过引入Lj的切片序列来克服该指数衰减的因子,解决了计算中出现的无界乘子问题。另外,在处理高阶项βuttt和非线性记忆项时,通过引入新的时变泛函F1(t)来估计关键的泛函F(t),从而得到F(t)的下界序列。最后对其迭代,证明了在次临界情况下解的爆破和生命跨度估计。
1 主要结果及证明
首先给出方程(3)能量解的定义。
定义1设(u0,u1,u2)H2(n)×H1(n)×L2(n),u是方程(3)在[0,T)上的能量解,如果uC([0,T),且满足


(4)

进一步,应用分部积分于式(4),可得


(5)
当t→T时,可得u满足方程(3)能量解的定义。
本文的主要结果如下:



ϒ(n,p,γ)=2-2γ+(n+3)p-(n-1)p2。
证明记
(6)
式(5)中,取φ(s,x)≡1,(s,x)[0,t]n且|x|≤R+s,得到

(7)
由式(7)可得
βF″(t)+F′(t)=βεF″(0)+εF′(0)+
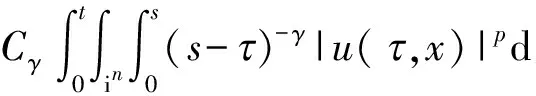
(8)
又对式(8)关于t求导,得到
(9)
因为支集u(t,·)⊂Bt+R(t(0,T)),应用Hölder不等式,可得

(10)

将式(10)代入式(9),得到

(11)
进行2次积分,可得
βF′(t)+F(t)-(βF′(0)+F(0))-(βF″(0)+F′(0))t≥

(12)
进一步对式(12)求积分,可得

(13)
接下来,将对F(t)的下界进行迭代,从而完成定理1的证明。需要指出的是,式(13)给出了迭代的框架。为了得到F(t)的第1个下界估计,引入Φ(x)函数[11]:
其中Sn-1为n-1维球面。该函数是正的光滑函数,且满足
ΔΦ(x)=Φ(x),Φ(x)~|x|-(n-1)/2e|x|,|x|→∞。
取Ψ=Ψ(t,x)=e-tΦ(x)。易知,Ψ满足βΨttt+Ψtt-ΔΨ-βΔΨt=0。泛函F1(t)定义如下:
(14)
应用测试函数Ψ于式(5),可得






(15)
由式(15),有

(16)
由F1(t)的定义,可以推出
(17)
将式(17)代入式(16),整理可得

(18)
其中

G′(t)+(1+δ)G(t)=εIβ[u0,u1,u2]+

(19)
对式(19)两边同乘 e(1+δ)t,积分,整理可得
(20)

类似地,对式(20)两边同乘 e2t,积分,可得
F1(t)≥
(21)
其中C为正常数。
由式(21)以及Hölder不等式,可得
(22)
其中p′为p的共轭指数。
利用Ψ的渐近性[8],可得
(23)
其中K>0。
联立式(22)、(23),有

(24)

由式(9)和式(24),可得

(25)

对式(25)进行2次积分,可得
(26)
其中,m1=βF′(0)+F(0),m2=βF″(0)+F′(0)。
式(26)两边同乘et/β/β,积分,整理可得
(27)
其中t≥β。

F(t)≥K0(R+t)-α0(t-β)γ0。
(28)
下面结合式(13)和迭代技巧推导F(t)的下界序列:
F(t)≥Kj(R+t)-αj(t-Ljβ)γj,
(29)
其中,t≥Ljβ;{Kj}j、{αj}j、{γj}j均为非负实序列;{Lj}j是具有收敛的无限积的部分积序列,其定义如下:
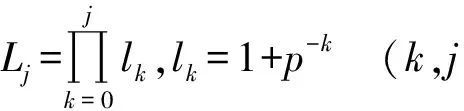
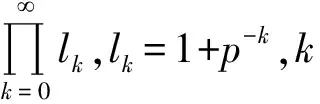
由式(28)可知,当j=0时,式(29)成立。假设式(29)对j≥0成立,下面证明式(29)对j+1也是成立的。
联立式(13)和式(29),有
Kjp(R+η)-pαj(η-Ljβ)pγj]dηdσdτds≥


Kjp(1-e-t(lj+1-1)/βLj+1),
(30)
其中t≥Lj+1β。
又
(31)
由式(30)、(31),可得
(32)
其中
(33)
式(32)表明式(29)对j+1成立。
下面将估计Kj。由式(33),可得
αj=n(p-1)+γ+pαj-1=…=(n(p-1)+γ)(1+p+p2+

γj=pγj-1+3=…=3(1+p+p2+…pj-1)+γ0pj=

(34)
因为
(pγj-1+1)(pγj-1+2)(pγj-1+3)≤(pγj-1+3)3=γj3,

(35)
联立式(33)~(35),有

(36)

对式(36)两边取对数,得到
logKj≥logD+plogKj-1-5jlogp≥logD+p(logD+
plogKj-2-5(j-1)logp)-5jlogp≥…≥(1+p+p2+ … +pj-1)×
logD+pjlogK0-5(pj-1+2pj-2+…+j)logp=
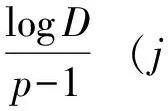
(37)
设j0=j0(n,p,γ)为下式成立的最小正整数:
由此,有

(38)
其中E0=E0(n,p,γ)>0。

结合式(29)、(34)和式(38),可得
F(t)≥exp(pjlog(E0εp))(R+t)-((γ/(p-1)+n+α0)pj-(γ/(p-1)+n))×

(R+t)-(γ/(p-1)+n)(t-Lβ)-3/(p-1),
(39)
其中,j≥j0,t≥Lβ。
取t≥max{R,2Lβ},则式(39)进一步化为
F(t)≥
exp(pj(log(E0εp2-((3+γ)/(p-1)+n+α0+γ0)t3/(p-1)+γ0-(γ/(p-1)+n+α0))))×
(R+t)-(γ/(p-1)+n)(t-Lβ)-3/(p-1)=
exp(pj(log(E1εpt3/(p-1)+γ0-(γ/(p-1)+n+α0))))×
(R+t)-(γ/(p-1)+n)(t-Lβ)-3/(p-1),
(40)
其中E1=E02-((3+γ)/(p-1)+n+α0+γ0)。
式(40)右边项中t的指数为
由γ(0,1),当n=1时,p>1;当n≥2时,1 设ε0=ε0(u0,u1,u2,n,p,γ,R,β)>0,有 t≥max{R,2Lβ},log(E1εptΥ(n,p,γ)/2(p-1))>0。 此时,式(40)中,令j→∞,则当ε(0,ε0以及t>E2ε-2p(p-1)/Υ(n,p,γ)时,F(t)的下界爆破。由此可知方程(3)不存在全局解。另外,可进一步推得u的生命跨度估计为 本文主要研究了MGT方程在非线性记忆项下解的爆破问题,通过迭代技巧得到了非线性记忆项对其柯西问题解的非局部影响。后续的工作将进一步讨论在临界情况下解的全局非存在性问题,此时需要重新构造新的时变泛函,因而问题会更复杂。


2 结束语

