二维Helmholtz方程的改进六阶紧致差分法

王肇君， 吴亭亭*， 曾泰山

(1. 山东师范大学数学与统计学院, 济南 250358; 2. 华南师范大学数学科学学院, 广州 510631; 3. 广东省大数据分析与处理重点实验室, 广州 510006)

Helmholtz方程是一类重要的物理方程,在电磁学[1]、声学[2]和地球物理[3]等科学领域有着广泛的应用。众所周知,Helmholtz问题的困难在于高波数问题[4]。对于高波数的Helmholtz问题,由于其解高度震荡,建立其高效和高精度的数值方法是困难的[5]。因此,寻求Helmholtz方程的高效数值解法具有重要的理论意义和应用价值。

目前,数值求解Helmholtz方程的方法主要有有限元法[5-8]、有限差分法[3,9-16]和谱元方法[17]等。其中,有限元法的精度高于有限差分法的,易于复杂边界条件和非均匀结构化的处理,但其计算量较大;有限差分法的计算简单、存储量小,易于实现。基于有限差分法,文献[18]针对高波数问题提出了一种并行预条件迭代法来求解 Helmholtz 方程,有效地提高了计算效率。由于高波数 Helmholtz 方程的解高度震荡,应用有限差分法求解高波数问题时常常受到非物理震荡的困扰,即所谓的“数值频散”。数值频散通常是由计算中采用粗网格引起的，因此,数值求解 Helmholtz 方程时,需要考虑数值频散和计算量。

近年来,求解 Helmholtz 问题的有限差分法得到了迅速的发展。为了提高差分法的数值精度,一方面,学者们提出了带参数的差分格式,并通过优化参数得到高精度的差分法[3,9];另一方面,学者们采用高阶差分格式来求解Helmholtz方程[10-13,15-16,19]。基于极小化数值频散的思想,文献[3,9]构造了求解Helmholtz方程的多种二阶差分格式:文献[3]利用旋转坐标系和借助加权平均的思想，建立了一种旋转九点差分格式，从而有效地抑制数值频散,提高数值精度;文献[9]基于点加权的思想,提出了一种带PML的Helmholtz方程的差分格式，该格式为二阶格式,且采用极小化数值频散的思想来得到差分格式的优化参数。紧致差分格式具有精度高、计算简单和对网格节点数要求不高等优点,因此受到了很多学者的关注。如:提出了多种四阶紧致有限差分格式[10-11,13,15,19];构造了二维Helmholtz方程的六阶紧致有限差分格式[12,16];通过对六阶紧致差分格式的截断误差进行二阶紧致逼近,从而得到一种高精度的紧致差分格式[12];采用9个点(中心节点及围绕该节点的8个节点)的加权平均来近似零阶项,以抑制数值频散[16];提出了三维Helmholtz方程的六阶紧致差分格式[14]。

本文主要构造了二维Helmholtz方程的一种六阶紧致差分格式。首先,给出了文献[16]的六阶紧致差分法的截断误差。然后,为了提高数值精度、减弱误差对波数k的依赖性,对所得截断误差的部分项进行二阶紧致逼近,从而得到一种改进的六阶紧致差分格式。其次,将改进的六阶紧致差分格式的误差方程进行转化,即将二维误差方程转化为若干个一维问题。在一维问题的基础上,证明了该格式在一定条件下的解存在唯一,且为六阶收敛的。再次,通过极小化数值频散的思想给出差分格式优化参数的加细选取策略。最后,给出2个数值算例来验证所提格式的精确性和有效性。

1 改进的六阶紧致有限差分格式

二维Helmholtz方程有如下形式

(1)

4um,n-2(um,n+1+um,n-1+um+1,n+um-1,n)]。

接下来,在文献[16]提出的六阶紧致差分格式的基础上,构造改进的六阶紧致有限差分格式。为此,先回顾文献[16]提出的六阶紧致差分格式。具体地,令

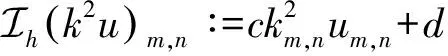
其中,c,d,e是满足c+d+e=1的参数。事实上,h(k2u)是k2u的二阶近似[20]。基于Equation-based方法[21]以及加权平均的思想[20],文献[16]对二维Helmholtz方程建立了如下六阶紧致差分格式

(2)

其中

利用 Taylor 展开可得该格式的截断误差为：

O(h8)。

(3)

易知,R满足

(4)

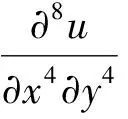
(5)

其中

证明首先,易知

(6)

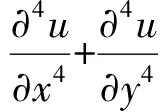
(7)

类似地,对Helmholtz方程(1)的两端关于y求二阶偏导,可得

(8)

将式(7)与式(8)相结合,可得

(9)

(10)

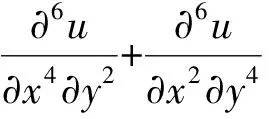
(11)

类似地,对式(8)的两端关于x求二阶偏导,可得

(12)

将式(11)与式(12)相加,可得

(13)

代入式(6),可得

(14)

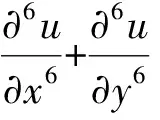
(15)

类似地,对式(8)的两端关于y求二阶偏导,可得

(16)

将式(15)与式(16)相加,可得

(17)

(18)

(19)

类似地,对式(16)两端关于x求二阶偏导,可得

(20)

将式(19)与式(20)相结合,可得

代入式(14),可得

(21)

(22)

对式(16)两端关于y求二阶偏导,可得

(23)

将式(22)与式(23)相加,可得

(24)

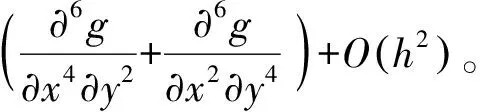
(25)

将式(6)、(10)、(14)、(18)、(21)、(25)代入截断误差R(3),即可得到命题的结论。证毕。

将截断误差(5)代入式(4)，可得:

(26)

其中

(27)

(28)

2 差分格式的收敛性分析

本节研究改进的六阶紧致有限差分格式(28)的解的存在性、唯一性和收敛性:首先，将二维误差方程转化为若干个一维问题;然后,证明了当k2不是-Δ的特征值且kh充分小时,差分格式(28)的解存在唯一;进一步地,证明了差分格式(28)为六阶收敛的。

为便于表述,考虑在方形区域Ω∶=(0,1)×(0,1)内进行收敛性分析。首先,引入一些记号。令步长h∶=1/N,N为正整数,并记N∶={1,2,…,N-1}。对于向量V=[Vm:mN],令

对矩阵W=[Wm,n:m,nN],定义其离散L2- 范数为：

(29)

对任意nN,定义Wn为矩阵W的第n个列向量,且有

其次,为了进行收敛性分析,给出差分格式(28)的误差方程。对任意m,nN,令Em,n∶=Um,n-um,n。将式(28)与式(26)相减,得到差分格式(28)的误差方程:

(30)

接下来,为了分析误差方程(30),将误差方程(30)转化为若干个一维问题。为此,引入矩阵D(N-1)×(N-1):

显然,三对角矩阵D是对称正定的,且D的特征值如下:

相应的特征向量为rn∶=[rm,n:mN]T,其中

(31)

事实上,特征向量组{rj,jN}是N-1空间的一组正交基。以下引理将误差方程(30)转化为N-1个一维问题。

引理1基于特征向量组{rj,jN},误差方程(30)可转化为N-1个一维问题:对任意jN,有

(32)

其中:

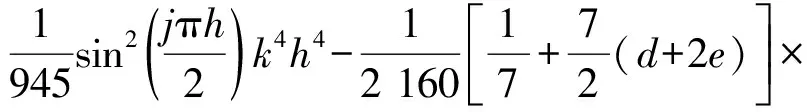
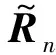
(33)

借助特征向量的分量表达式(31),由式(33)知,对任意m,nN,有:

(34)

下面考虑一维问题(32)的解的存在唯一性,并给出收敛性分析。

引理2假设k2不是-Δ的特征值。对于任意jN,当kh充分小时,一维问题(32)的解存在且唯一,且有以下估计式

(35)

其中,C为某一常数。

其中,Hj是一维问题(32)的系数矩阵。由于Hj是三对角托普利茨矩阵,由文献[22]可知

(36)

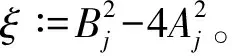
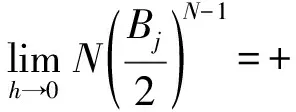
所以,当ξ=0时,有det(Hj)≠0。当ξ>0时,由式(36)知det(Hj)≠0。接下来,证明当ξ<0且kh充分小时,det(Hj)的值不为零。当ξ<0时,由式(36)得:

因此,可以得到

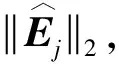
其中,C1为正常数。因此

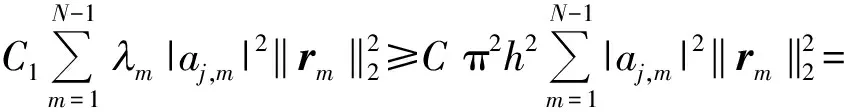
(37)

(38)

联立式(37)和式(38),即得引理的结论。证毕。

最后,给出差分格式(28)的解的收敛性分析。

定理1假设k2不是-Δ的特征值。当kh充分小时,差分格式(28)的解U存在且唯一。若在狄利克雷或诺伊曼边界条件下的Helmholtz方程(1)的解u在求解区域Ω上满足u则有

‖|u-U|‖≤Ch6,

其中,U∶=[Um,n:m,nN],u∶=[um,n:m,nN],C是依赖于u的常数。

证明下面只给出狄利克雷边界条件下的证明,在诺伊曼条件下的证明类似可得。为证明差分格式(28)的解存在且唯一,首先分析误差方程(30)。引理1说明了误差方程(30)可以转化为N-1个一维问题(32)。由引理2可知,当kh充分小时,一维问题(32)的解存在且唯一。因此,当kh充分小时,误差方程(30)的解也是存在唯一的。所以,当kh充分小时,差分格式(28)的解存在且唯一。

令E∶=[Em,n:m,nN],m,n:m,nN]。为了对差分格式(28)进行收敛性分析,只需估计‖|E‖。首先,根据范数的定义和内积的性质,有

(39)

(40)

对式(39)的右端应用式(35),并结合式(40),可得

(41)

定理得证。

由截断误差的表达式(27)知,当kh充分小时,差分格式(28)的误差仅依赖于函数u,对波数k的依赖性较弱。

3 差分格式的参数优化选取策略

本节给出差分格式(28)的频散方程。从频散方程出发,基于极小化数值频散的思想,给出差分格式(28)的优化参数的加细选择策略。

为了得到优化参数d和e,首先给出差分格式(28)的频散方程。为此,将差分格式(28)进行改写。为便于分析,引入以下记号:

(

W

)

m,n

∶=

W

m+1,n+1

+

W

m-1,n-1

+

W

m+1,n-1

+

W

m-1,n+1

,

(

W

)

m,n

∶=

W

m+1,n

+

W

m-1,n

+

W

m,n-1

+

W

m,n+1

。

从而将差分格式(28)改写为:

A0Um,n+A(U)m,n+A

(42)

其中,

A∶=

接下来,对差分格式(28)进行频散分析。为此,令g=0,并将Um,n∶=e-ik(xmcos θ+ynsin θ)代入差分方程(42),利用欧拉公式得频散方程:

4APQ+2A(P+Q)+A0=0,

(43)

其中,P∶=cos(khcosθ),Q∶=cos(khsinθ)。

标准化的数值相速度和标准化的数值群速度是衡量数值频散的重要标准[3]。在实际应用中,常用标准化的数值相速度来作为衡量数值频散的标准。对于有限差分法,当其标准化的数值相速度越接近1时,其数值频散越小,相应的数值精度越高。由文献[20]可知，要得到标准化数值相速度kN/k,需要获得数值波数kN。然而,对于差分格式(28),很难获得其数值波数kN。因此,借鉴文献[16]的方法,直接从频散方程出发来获得差分格式的优化参数。

为了得到差分格式(28)的优化参数,再次考虑频散方程(43)。令v为波传播的相速度,λ为波长,G∶=λ/h为每个波长的网格节点数。由λ=2πv/ω,k=ω/v，可得kh=2π/G。在频散方程(43)两端同时乘以h2,并用2π/G替代kh,可得:

(44)

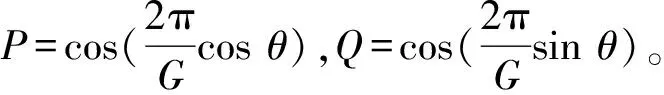
加细选择策略:

步骤1： 估计区间IG∶=[Gmin,Gmax],其中Gmin代表G的最小值,Gmax代表G的最大值。令

其中，n=1,2,…,s；s为给定的正整数。

步骤3： 将1/G和θ代入方程(44),得到一个超定方程组。

步骤4： 应用最小二乘法求解得到的方程组,即可得到差分格式(28)的优化参数。

4 数值算例

下面将通过2个数值算例来验证本文提出的改进六阶紧致差分格式的有效性。在本节中,数值解与精确解之间的误差用离散L2-范数(式(29))衡量。根据经验将区间[2.5,400]划分为7个小区间，基于加细选择策略，对于部分区间IG，得到差分格式(28)的多组加细的优化参数(表1)。在下面的计算中，均采用表1中的参数作为差分格式(28)的优化参数。将本文提出的差分格式(28)(简记为IC6)与文献[16]构造的带优化参数的六阶紧致差分格式(简记为OC6)进行了数值精度的对比。

表1 加细的优化参数Table 1 The refined optimal parameters

问题1考虑二维 Helmholtz 方程

Δu+k2u=-a2sin(ax)sin(ky),(x,y)Ω∶=(0,π)×(0,π),

其边界条件为

u(x0,y0)=0,(x0,y0)Γ∶=∂Ω。

假设a、k为正整数，该问题的真解为

u(x,y)∶=sin(ax)sin(ky),(x,y)[0,π]×[0,π]。

a=1,k=24;a=3,k=24 和a=3,k=48 时,不同网格剖分下所对应的 2 种差分格式的离散L2- 范数误差 (表2至表4)表明:与OC6相比,IC6的数值精度有较大的提高;在参数a相同的情况下,IC6的数值精度对波数k的依赖性弱于OC6的,与前面的理论分析结果一致。a=1,N=256时,不同波数k所对应的2种差分格式的离散L2-范数误差(表5)表明:当网格剖分N固定,随着波数k的增大,OC6与IC6的离散L2-范数误差都有所增大,但是与OC6 相比,IC6 的数值精度依然有显著的提高。此外,离散L2-范数误差曲线图(图1)表明了2种差分格式的误差曲线与斜率为-6的直线近似平行，说明2种差分格式均为六阶格式。

表2 a=1,k=24 时的离散 L2- 范数误差Table 2 The error in the discreteL2- norm for a=1,k=24

表3 a=3,k=24 时的离散 L2- 范数误差Table 3 The error in the discreteL2- norm for a=3,k=24

表4 a=3,k=48 时的离散 L2- 范数误差Table 4 The error in the discreteL2- norm for a=3,k=48

表5 a=1,N=256 时的离散 L2- 范数误差Table 5 The error in the discreteL2- norm for a=1,N=256

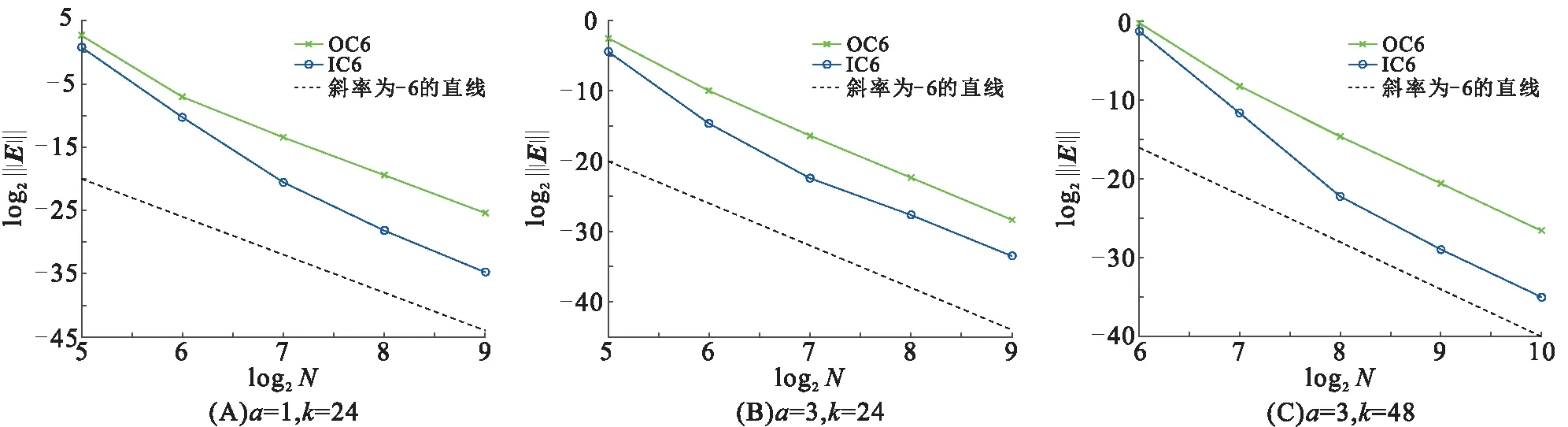
图1 问题1的离散 L2- 范数误差曲线

问题2考虑二维 Helmholtz 方程

Δu+k2u=0,(x,y)Ω∶=(0,π)×(0,π),

其边界条件为

假设k为常数,则上述问题的真解为u=eiβysinx,且有 12+β2=k2。在y=π 处使用 Sommerfeld 型边界条件uy-iβu=0的原因是:将特征值移到复平面,从而消除在实特征值处发生共振的可能性[23]。因此,对任意k>0,该问题的解存在且唯一。

β=100,k=100.005 0;β=199.997 5,k=200和β=499.999 0,k=500时不同网格剖分下所对应的2种差分格式的离散L2-范数误差(表6至表8)表明:与OC6相比,IC6的误差明显减小,说明IC6的数值精度高于OC6的。N=700时,不同波数k所对应的2种差分格式的离散L2-范数误差(表9)表明:随着波数k的增大,OC6和IC6的离散L2-范数误差都有所增大,但是IC6的数值精度依然高于OC6的。此外,离散L2-范数误差曲线图(图2)表明2种差分格式的误差曲线与斜率为-6的直线近似平行，说明2种差分格式均为六阶格式。

表6 β=100,k=100.005 0时的离散 L2- 范数误差Table 6 The error in the discreteL2- norm for β=100,k=100.005 0

表7 β=199.997 5,k=200 时的离散 L2- 范数误差Table 7 The error in the discreteL2- norm for β=199.997 5,k=200

表8 β=499.999 0,k=500 时的离散 L2- 范数误差Table 8 The error in the discreteL2- norm for β=499.999 0,k=500

表9 N=700 时的离散 L2- 范数误差Table 9 The error in the discreteL2- norm for N=700

图2 问题 2 的离散 L2- 范数误差曲线

5 结论

本文建立了二维 Helmholtz 方程的一种改进的六阶紧致差分格式,该格式的特点是其误差较弱地依赖波数k,收敛性分析表明该格式是六阶收敛的。数值算例验证了该格式可以有效地提高数值精度,抑制数值频散。