以“说理”为抓手 促算法形成
文/乐昌市乐城第一小学 尹秀兰
小学数学计算教学可以通过说算理、明算法的方式,培养学生运算能力及解决问题的能力。教学过程中,教师要引导学生主动参与“说理”,经历知识的形成过程,达到“授人以渔”的目的,并让学生通过表达,加深对算理的理解,不断发展他们的理性思维和理性精神。下面以两位数乘两位数的计算教学为例进行探讨。
一、乘得的积与谁对齐?
北师大版小学数学三年级下册的《乘法》单元的重点就是两位数乘两位数的计算方法,可以引导学生在交流算法的过程中理解算理。
如学生在计算“14×12”时,总是会把积写在个位上,看上去是算法的错误,实际上是对算理不理解。如何让学生理解?可以借助课本中的点子图(见图1),先说一说“14×12”的计算过程:将12排点子分成2排和10排,先算14乘2得到28,再算14乘10得到140,最后把所得的积相加得到168。

图1
二、从哪位开始乘?
在学习第三单元《乘法》第三课时,教师可能会发现像“21×14”这样的题,学生练习时正确率100%,而像“24×56”这样的题,就有部分学生做错。通过观察学生计算过程和追问,我们不难发现做错的学生是从高位开始算起。反观教学过程,我们会发现,数学课本上第二课时的例题中的点子图和表格计算方法都是从高位开始计算的。
在教学时怎样让学生明白要从个位算起,为什么要从个位算起?我们可以进行对比教学,在练习时出示“21×32”“27×53”,让学生分别进行计算。汇报时,学生会发现“21×32”既可以从个位开始乘,也可以从十位开始乘;而“27×53”只能从个位乘起,从十位开始乘就算不下去,因为“5×7”有进位,“2×5”也有进位,需要不断进行修改,非常不方便。
到底该怎么算?这时让学生充分讨论,然后通过比较、辨析、说理,引导他们了在自我否定中领会正确的做法,理解从高位开始算不是错的,只是不适用于所有的两位数乘法,一般情况下应该从个位开始算。
三、怎样处理末尾的“0”?
个“理”在学生学习两位数乘以整十数的时候就要讲清楚了。
教学三位数乘两位数时,会发现学生在列竖式时习惯末位对齐,就算三位数的末尾是“0”。回顾三年级下册《乘法》单元的第一课时,就是两位数乘整十数,教材中并没有呈现竖式方法,而是通过找规律口算(见图2)得到结果。
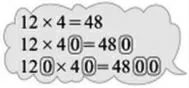
图2
当没有规律可循时,学生就不知道怎样处理这个“0”比较简便,如果只是简单告诉学生列竖式时可以先把“0”放一边,可将47的7与210的1对齐。学生不明白为什么十位的1和个位的7可以对齐,如果只是简单的模仿,那他们不但记不住这种简便算法,还会质疑:乘法竖式不是应该末位对齐吗?因此这
例如计算“56×30”,可以先让学生自己计算,口算能力强的学生可能直接口算,也有学生会利用以前学过的两位数乘一位数的经验列竖式计算,可能会出现这样的情况(如图3)。这时让学生观察竖式,说一说:在第一步计算时为什么会出现“00”,这个又有什么意义?当学生说出“0”没有意义的时候,老师应当追问:既然“0”没有意义,那我们就不要,可以吗?

图3
通过说理,让学生明白算式中的“00”虽然没有意义,但个位上的“0”起到了占位的作用,如果去掉的话,那结果就变成了168,比正确的结果缩小了10倍。最后再让学生交流喜欢用哪种方法计算,通过比较,让学生总结出末位是“0”时,怎样算更简便合理。
在计算教学中引导学生“说理”,让学生有表达的机会,让知识有构建的过程,才能让他们真正掌握数学的本质,培养他们想数学和说数学的能力,促进算理理解和算法掌握。

