基于RNN-RBM 模型的配网馈线长期负荷预测方法

杨剑文 朱 林 林凌雪 吴子龙 陈元榉 陈展纶

(1.华南理工大学 电力学院,广州 510640;2.广东电网有限责任公司 广州供电局,广州 510600)

长期负荷预测是电力公司系统规划活动的基础[1],能引导电力公司以经济有效的方式规划长期的基础设施升级或改造.配网馈线长期预测是其中的重要一环[2-3],必须加以重视.国内外对长期负荷预测进行了大量的研究,文献[4]提出了一种堆叠长短期记忆循环神经网络模型,对多尺度的负荷数据进行预测,文献[5]提出了一种基于历史天气的区域电网负荷预测模型,文献[6]采用元胞自动机技术对农村用电负荷进行预测,文献[7]基于有序充电思路利用非线性规划算法对居民区电动汽车进行中长期充电负荷预测,文献[8]采用支持向量机和改进灰色GM(1,1)模型实现了中长期氢负荷预测.

总的来说,长期负荷预测方法可分为自上而下和自下而上两种模式.自上而下预测模式侧重于预测整体层面的用电量.例如,文献[9-11]采用单变量回归模型ARIMA 模型来直接分析负荷变化趋势,但忽略了经济、人口和天气等外部变量的驱动力.为了解决这一不足,也有学者引入多元回归模型分析这些外部变量与负荷变化之间的关系,如模糊神经网络(FNN)[12-15],BP神经网络[16-17]和随机森林模型[18-19]等.此类方法适合预测区域负荷整体水平的场景,但没有考虑馈线的特征信息,故而应用于配电馈线预测时会存在一定不足,例如在整体负荷分配给各个馈线的过程中,无法明确各馈线之间的关系,而配电线路峰值需求受负荷的影响较大,这样必然与整体负荷有较大偏差.因此,针对配网馈线的长期负荷预测需求,自上而下的预测模式只能为具体馈线的预测和调整提供整体参考.自下而上的预测模式通过收集底层馈线负载信息来进行[20].负载信息通过直接统计用户负荷来获得,通过新负荷的预期大小来估计每年馈线负荷变化,实际工作中会聚焦对馈线负荷变化影响巨大的大客户负载变化,但客户信息不可靠或预测期间客户计划的变化均会影响预测结果.文献[21-22]提出了一种基于部分负荷预测的方法,即先将部分负荷分别预测,然后再聚合到整体进行集群预测,但该方法依然没有考虑到外部因素对负荷变化的影响.

由上述分析可知,面对馈线长期负荷预测采用单一预测模式均会存在不足:自上而下的预测模式会忽略馈线的特征信息,只能为具体馈线的峰值预测提供整体参考;而自下而上的预测模式又缺乏考虑外部因素对负荷的驱动作用.事实上,将两种模式下的特征以及历史负荷数据有效地融合,是打破目前工作瓶颈的有效途径.

1 配网馈线长期负荷预测基本思路

本文提出了一种基于RNN-RBM 模型的配网馈线长期负荷预测方法,基本思路如图1所示.

图1 配网馈线长期负荷预测基本思路

输入数据包括自上而下特征(经济、人口和温度等)、自下而上特征(大客户负荷和馈线负载组成)以及历史负荷数据.首先,通过参考文献[23]的方法对历史负荷数据进行缺失值插值和异常数据剔除,完成相关数据预处理工作.其次,将不同类型的特征归一化到同一数值尺度,再运用主成分分析对相关特征进行降维,提高模型训练效率,避免过拟合问题,提出虚拟馈线方法解决负荷转移问题.再次,通过模型评估和网络参数调整,建立RNN-RBM 预测模型.然后,将处理好的数据和特征输入模型进行预测.最后,根据选用的评价指标进行预测结果分析.

2 特征选择和处理

2.1 特征选择

特征选择是建立预测模型的第一步,目的是分析和选择与问题相关的原始特征.本文从自上而下和自下而上两个方面选择了与配电馈线需求相关的特征.

2.1.1 自上而下的特征

自上而下的特征描述了预测区域的总体驱动因素,会考虑年经济、人口和温度特征.其中,历史和未来的经济和人口特征通常可以从政府机构公开的信息获得,而历史温度来自气象统计数据.

1)经济特征:与短期电力需求不同,长期电力需求与当地经济密切相关.本文主要考虑年实际地区生产总值增长率(%)特征和总就业增长率(%)特征.

2)人口特征:人口规模显著影响住宅负荷增长.即使经济放缓,稳定的人口规模仍然可以支撑稳定的住宅负荷水平.此外,人口增长可能导致住宅开发,进而促进电力发展.而且作为人口的一部分,劳动力反过来影响经济活动,并与总就业增长有关.因此,本文选择人口增长率(%)作为人口特征.

3)温度特征:一般选择夏季最高温度或者冬天最低温度.因为夏季用电高峰和冬季用电高峰与制冷和制热用电的极端温度相一致.考虑到制冷几乎全是依赖于电力能源,但制热可能依赖于其他能源,比如天然气,所以本文采用夏季最高温度作为温度特征.

2.1.2 自下而上的特征

自下向上的特性描述了详细的馈线层信息,本文将考虑大客户净负荷变化和馈线负荷组成.

1)大客户净负荷变化:指的是馈线上所有大客户的预计净负荷变化,即馈线上来自大客户的所有报告的负荷变化的总和.其中大客户包括工厂、购物中心、办公楼和新住宅区.

2)馈线负载组成:配电馈线上有不同类型的负载,考虑住宅负载、商业负载和工业负载3类.其中,住宅负荷与温度和人口的关系更大,工业负荷与经济的关系更大.

馈线住宅峰值负荷百分比Z的计算见式(1):

式中:PF是前一年的馈线高峰负荷为住宅负荷i在前一年馈线峰值时刻的负荷;n是此馈线上住宅负载的总数.

馈线商业峰值负荷百分比S的计算见式(2):

式中:PF是前一年的馈线高峰负荷为商业负荷i在前一年馈线峰值时刻的负荷;m是此馈线上商业负载的总数.

工业负荷百分比G可由式(3)计算得出:

最终,初步选择的特征见表1.

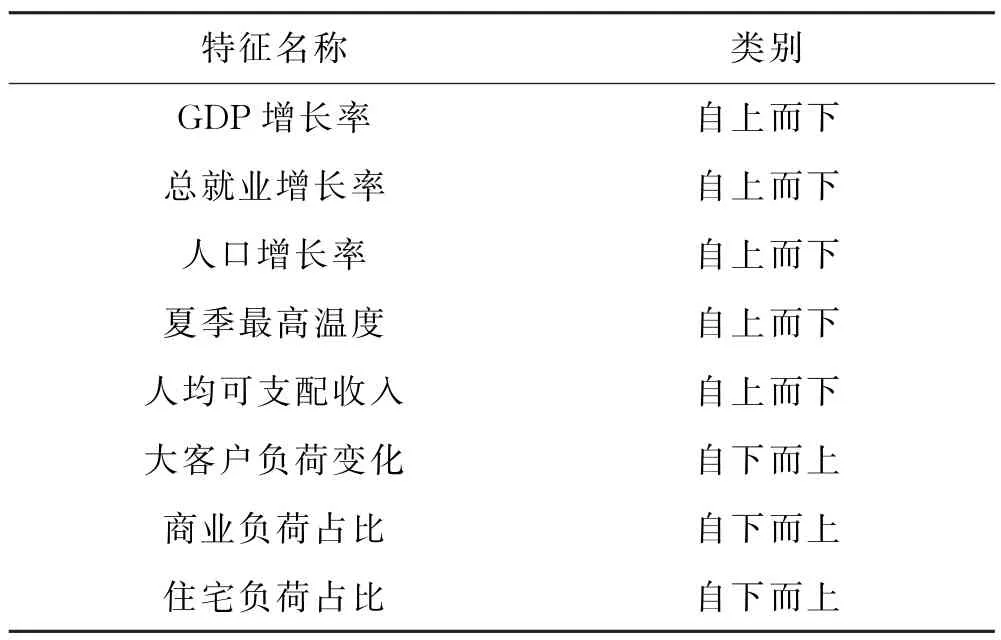
表1 模型初选特征

2.2 特征处理

特征处理是将以上讨论的原始特征转化为合适的特征,以便输入到之后的训练模型中.其目的是消除数据噪声,降低模型复杂度,提高模型精度.

2.2.1 归一化处理

上述讨论的特征使用不同的单位量纲,它们之间有很大的幅度差异,因此还需要归一化处理.本文选用最小-最大归一化方法,见式(4),可将特征归一化到[0,1]的取值范围.

式中:特定特征Xnorm是归一化之后的值;XRaw是归一化前的值;Xmax是该特征的最大观测值;Xmin是该特征的最小观测值.

2.2.2 特征主成分分析

表1中的特征虽然体现在不同领域、不同方面,但是也存在内部联系.例如,就业增长可以刺激国内生产总值增长,亦导致在人口、可支配收入上的增长.考虑到特征间的关联,可以依据主成分分析来聚合降维,不仅降低特征间的冗余信息,而且可缩短模型训练时间,提升整体效率.

本文采用文献[24]所提的主成分分析法,将在常规正交坐标系的变量通过矩阵变换操作映射到另一个正交坐标系中的主元,从而减少了变量间的线性相关性.设有n组数据,每组数据有p个变量.基本步骤如下:

1)对数据进行标准化处理

在实际应用时,指标的量纲往往不同,所以在进行主成分计算之前先要进行标准化处理,通过数据变换来消除量纲的影响,见式(5):

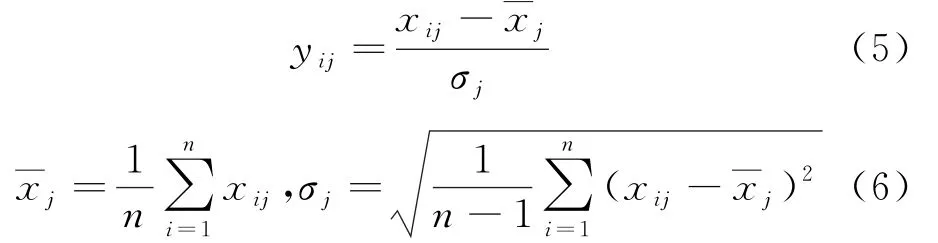
式中,i=1,2,…,n;j=1,2,…,p.

无论是歌舞音乐还是说唱音乐，其少数民族音乐都有着十分强烈的民族特性：感情深沉、气息宽阔、旋律优美。就表现形式来看，有丰富的长短调民歌以及民族歌舞剧、歌舞音乐、说唱音乐等，这些音乐表现形式都具有十分强烈的民族性。就内容来看，有着十分丰富的种类，如儿歌、叙事歌、短歌、礼俗歌、思乡曲、赞歌、狩猎歌；舞蹈有孔雀舞、甩发舞、蜂桶鼓舞、象脚鼓舞等，这些内容将民族音乐特点以及民族文化传统都淋漓尽致地体现出来。就风格来看，其音乐多是旋律明快、节奏活泼，民族气息强烈，歌曲的曲风表现也非常明显突出。

2) 建立相关矩阵R,见式(7):

式中:Y为标准化后的数据矩阵.

求特征值和特征向量,并将特征向量按照特征值大小进行排序,组成特征向量矩阵α:

3)计算累积方差贡献率β(k),通过β(k)＞95%筛选出k个独立特征:

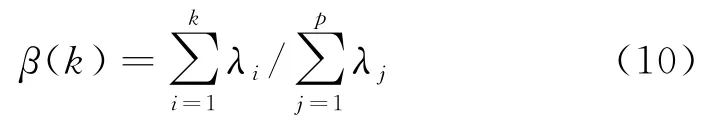
4)获得主成分矩阵Z=Yα

利用主成分分析,在累积方差贡献率为95.85%下可将就业增长率、GDP 增长率、人口增长率、人均可支配收入这4个特征压缩为2个独立特征,见表2.进行特征处理后的最终模型输入特征见表3.

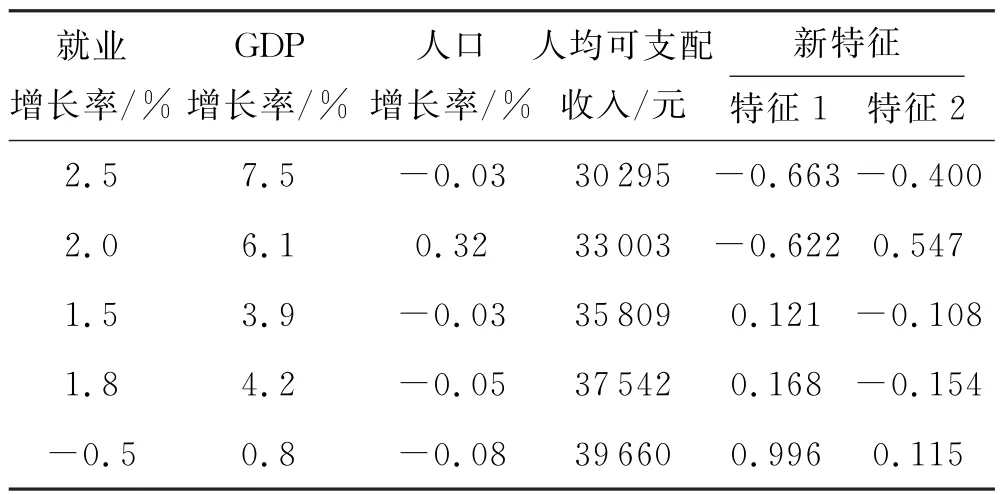
表2 特征主成分分析

表3 最终模型输入特征

2.2.3 虚拟馈线方法

在实践中,影响馈线峰值特性的一种重要数据噪声来自相邻馈线之间的负荷转移情况.例如,当馈线A 的负荷接近其容量约束时,会将位于馈线A 的馈线分支上的用户转移到相邻的馈线B上,以便馈线A和B 可以继续可靠地为其用户提供服务.这种情况下,负荷转移使馈线A 的负荷突然下降,馈线B的负荷突然上升.这种变化偏离了之前馈线和馈线的负荷趋势,与前面讨论的自上而下和自下而上的特征无关.

为了解决这一问题,本文提出了虚拟馈线的概念.该方法将保证馈线负荷特征趋势的连续性.对于存在负荷转移情况的馈线,可以生成一个虚拟馈线,其负荷值为发生负荷转移事件的相邻馈线的平均值,见式(11):

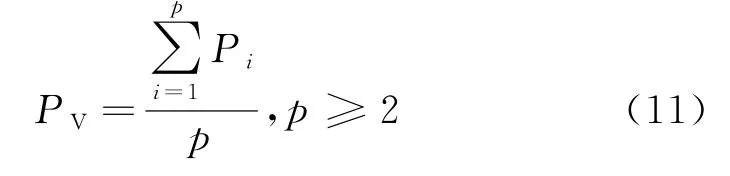
其中:PV为虚拟馈线的最大峰值负荷值;Pi为发生负荷转移的第i条馈线的最大峰值负荷值,p一般为2.

3 基于RNN-RBM 长期负荷预测模型

3.1 问题描述

配网馈线长期负荷预测问题需要分析输入的负荷数据和特征信息的高维时序非线性映射关系.同时,长期负荷预测数据大都是以年为计量单位来统计的,存在数据稀疏问题.

RNN 有着强大的记忆功能,方便处理任意时序的输入序列,可以捕获多变量时间序列之间的时间自相关特征;而RBM 有强大的无监督学习能力,能够描绘数据中复杂的规则,可以有效拟合离散分布.可以结合RNN 和RBM 的特点来构造出RNN-RBM模型[25],该模型不仅可以更全面地分析特征与负荷变化的内在联系,而且还可以将离散特征序列映射到连续空间来评估下一样本出现的概率,从而解决数据稀疏的问题.可见,RNN-RBM 模型的优势非常契合配网馈线长期负荷预测的场景需求.

3.2 RNN-RBM 模型建立

将第2节处理好的负荷数据和特征输入给RNN网络,由RNN 网络来进行时序特征处理,输出值作为RBM 的输入.利用RBM 强大的描绘复杂分布的能力,以无监督的模式训练输入进来的样本,从而生成新的样本空间,最终进行预测.RNN-RBM 模型如图2所示.

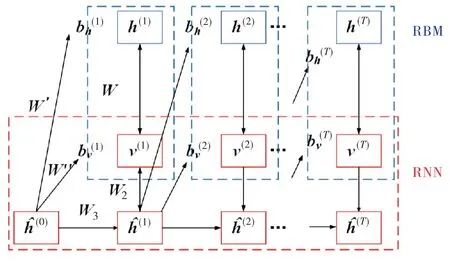
图2 RNN-RBM 模型

在图2所示的结构图中,红色框内是沿时序展开的RNN 网络,每一个蓝色框内是一个RBM.模型中,h(T),v(T)和分别为RBM 隐藏层、RBM 可 见层和RNN 网络中包含的神经元个数为RBM隐藏层的偏置向量为RBM 可见层的偏置向量;W为RBM 隐藏层和可见层之间的权重;W2为RBM 可见层与RNN 网络中相对应神经元之间的权重;W3为RNN 网络中神经元之间的权重;W＇为RBM 隐藏层与RNN 网络神经元之间的权重;W″为RBM 可见层与RNN 网络神经元之间的权重.

从图中可以看出,模型当前时间步长的输出不仅基于当前输入,而且还基于之前的时间步长信息,非常适用于预测问题.正如馈线长期负荷预测问题,当前的电力需求往往不仅与当年有关,还与过去几年的条件和势头有关.

h和v之间相互生成的条件概率,见式(12)、(13):

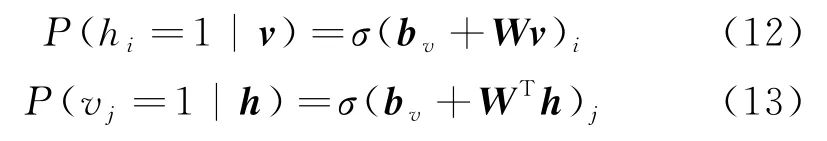
其 中:σ为sigmoid函 数.

RNN-RBM 的联合概率分布见式(14):

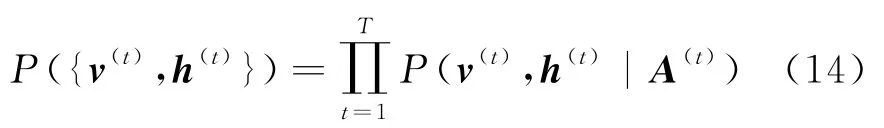
式中:P(v(t),h(t)|A(t))代表第t个RBM 的联合概率,参数由式(15)～(17)定义:

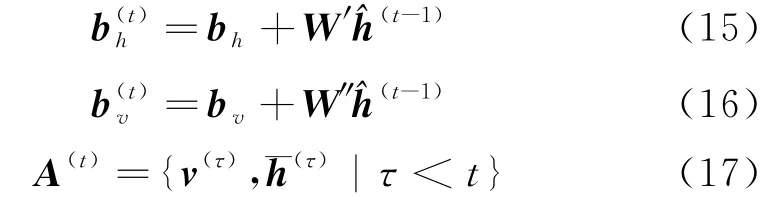
式中:A(t)为所有t时刻之前的{v,h}集合,其中为h(t)的平均值.

RNN 部分就是一个单层的沿时序展开的RNN网络,隐藏层单元计算式见式(18):

针对配电网馈线长期负荷中多特征变量的时间序列特点,本文采用交叉熵作为模型的损失函数,见式(19).

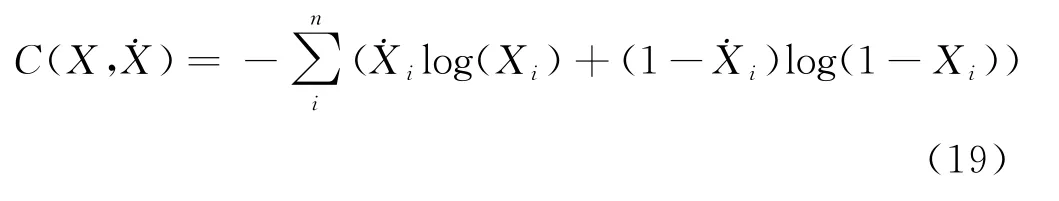
其中:X为输入数据的分布;为拟合模型重构数据的分布.

该损失函数通过计算输入数据与RNN-RBM 模型重构数据之间的概率分布差异,可以量化模型在训练集中的准确性.

3.3 评价指标

为了评估预测的性能,本文设置平均绝对百分比误差EMAP为评价指标,见式(20):

式中:n为预测总次数;xact(i)和xpred(i)分别为i时刻的负荷真实值和预测值.

4 算例分析

为了验证本文所提RNN-RBM 模型的有效性和准确性,算例以广州市某地区2009—2020年475条馈线最大峰值负荷和年度经济以及气象数据为数据集.其中184条存在负荷转移情况,转换为84条虚拟馈线,有291条馈线不存在负荷转移情况;选用如表3所示的特征,进行负荷预测;最后在同一数据集的基础上,将仿真结果与随机森林模型以及LSTM 网络模型预测结果进行对比分析,证明本文所提模型预测结果的准确率更高.

4.1 仿真设置

工作站硬件处理器为Intel Xeon E5,内存为64 GB,采用Tensorflow 软件框架(版本1.12.1).模型参数的具体设置见表4.

表4 模型参数设置

选用文献[26-29]方法,设置两种对比模型的参数.其中,随机森林模型中决策树个数为100,最大特征数为8;而LSTM 循环神经网络中隐藏神经元24个,输出神经元16个.

4.2 预测结果分析

对上述模型进行训练,限于篇幅,这里仅展示了RNN-RBM 模型的情况,其损失函数下降曲线如图3所示.可以看出,RNN-RBM 已经训练收敛.另外两个模型均也训练收敛.

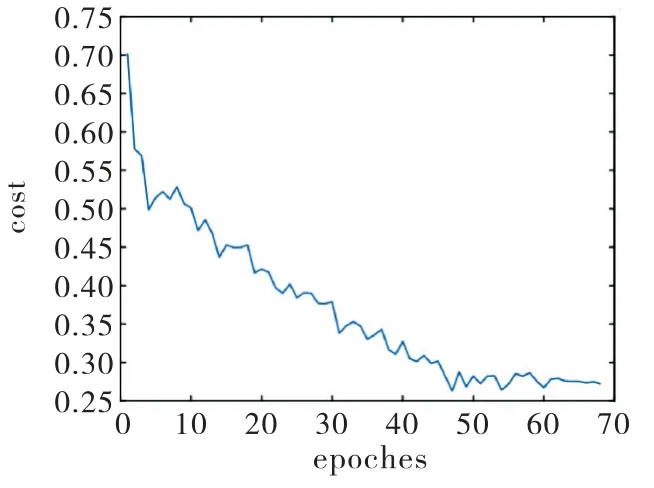
图3 RNN-RBM 模型损失函数下降图

本文对2020年的馈线负荷进行长期负荷预测,图4为不同算法模型预测值与实际值的对比图,其中图4(a)为所有馈线预测值与实际值的对比图,图4(b)为其中节选的20条馈线的预测值与真实值的对比图.图5为某条馈线历史数据与预测年(2020年)真实数据、各模型预测结果构成的对比图.从图中可以看出,通过对样本特征的深层挖掘与学习,本文所提的RNN-RBM 模型预测精度最高.

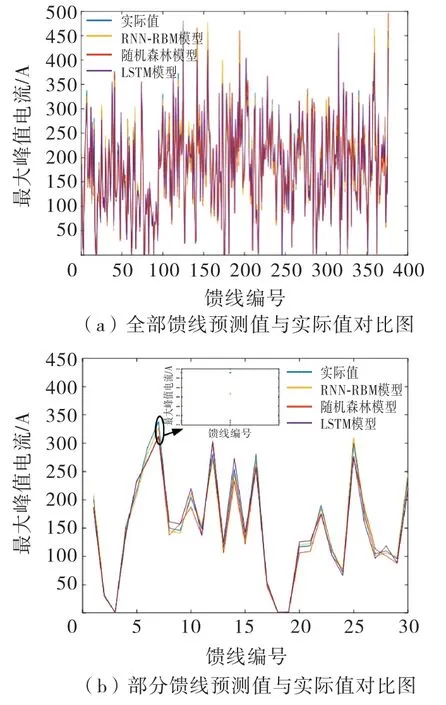
图4 不同模型馈线预测值与实际值对比图

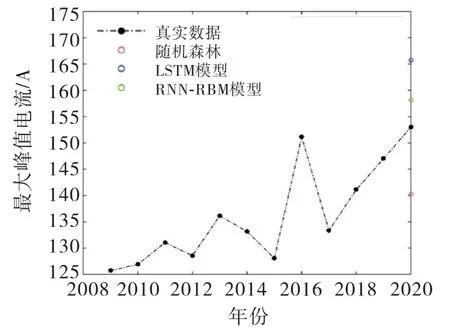
图5 2020年某条馈线历史数据与预测值对比图

将不同算法模型下的预测值与实际值进行汇总比较,并考察引入的EMAP指标,结果见表5.可以看出,本文所提模型的精准度最高.

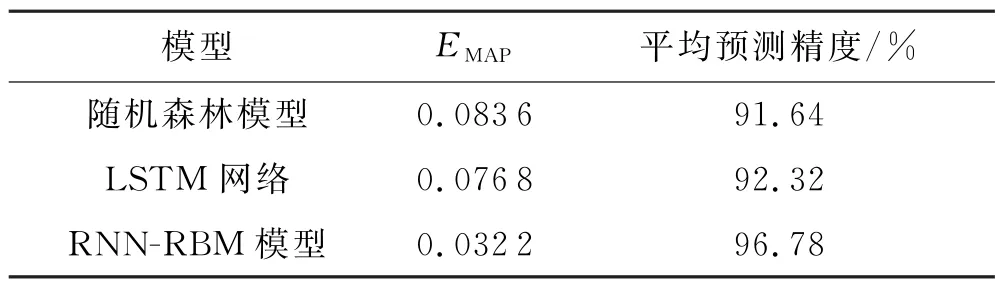
表5 不同模型预测结果

5 结论

本文提出了一种基于RNN-RBM 网络混合模型的配电馈线长期负荷预测方法,并在实际配电网中进行了验证,结果表明:

1)混合采用自上而下和自下而上两种模式,通过主成分分析来压缩冗余关联,通过虚拟馈线方法解决负荷转移问题,所构造的特征信息可满足配电网馈线长期负荷预测需求.

2)通过RNN-RBM 模型可挖掘负荷数据时序性和复杂特征关系的内在关联,提升了馈线长期负荷预测的精度.

在未来的研究中,本文的相关研究还可以扩展到其他类型的预测问题上,为配电网的设计规划和高级分析等提供数据基础.