一类递归神经网络系统的有限时间同步

阮泽宇 胡军浩 梅 俊

(中南民族大学 数学与统计学学院,武汉 430074)

递归神经网络作为一种非线性电路网络系统[1],近年来得到了广泛的研究与关注,并被成功地应用于各种领域,如联想记忆[2]、图像处理[3]和模式识别[4].神经网络能够模拟大脑,为超级人工智能神经计算机奠定了基础.在神经网络的实际应用中,其系统稳定性和同步现象是一个非常重要的动力学行为,受到了许多学者的关注和研究.学者们提出了许多有效的控制方法研究神经动力系统,如自适应控制[5-6]、滑模控制[7-8]、脉冲控制[9-10]等.

间歇控制是介于连续反馈控制和脉冲控制之间的一种不连续控制.同连续反馈控制相比,能有效降低控制成本[11];同脉冲控制相比,能提高控制性能.因此,间歇控制作为一种间断控制方法,具有成本效益高、控制能力强等优点.该控制方法的工作原理是将工作时间分为两部分:控制区间和非控制区间,在控制区间工作,在非控制区间关闭.

间歇控制作为一种典型的时间触发控制策略,其控制区间是预设的,而事件触发只有在系统状态满足触发条件时才进行各种操作,可以有效降低通信带宽,节约能源.事件触发控制更符合实际情况,可以避免资源浪费.因此,事件触发间歇控制[12]可以在不同程度上克服时间触发控制的一些缺陷.

有限时间同步[13-14]具有较强的抗干扰能力,收敛速度快,控制效率高.上述文献主要研究指数或渐近同步,很少有文献研究事件触发间歇控制的有限时间同步,所以研究基于事件触发控制的神经网络系统的有限时间同步具有重要的理论价值和实际意义.

符号说明:R 表示实数空间,Rn,Rn×m分别表示n维欧式空间和n×m实矩阵空间;PT表示P的转置;矩阵P＞0表示P为正定矩阵;‖·‖表示欧几里得范数;λmax(A),λmin(A)分别表示矩阵A的最大,最小特征值;N 表示自然数集合.

1 模型描述与准备知识

考虑如下由电子线路实现的Hopfied递归神经网络:

其中在电路网络中,xi(i=1,2,…,n)表示第i个神经元在t时刻的输入电压;Ci为第i个神经元的细胞膜输入电容;Ri为跨膜电阻;Rij=(bij)-1为确定阻抗为放大器的输出电压;wi为外加偏置电流.

可以改写为如下形式:

其矩阵形式为:

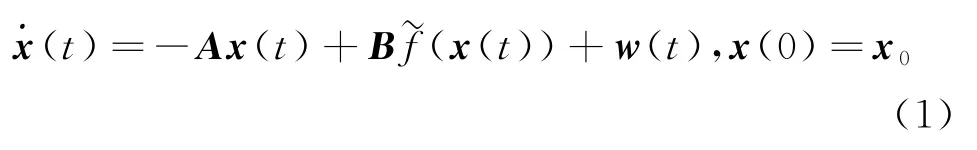
其中:x(t)=(x1(t),x2(t),…,xn(t))T∈Rn表示系统的状态向量;xi(t)(i=1,2,…,n)为第i个神经元在t时刻的状态;B=(bij)n×n∈Rn×n是连接权重矩阵;A=diag(a1,…,an)∈Rn×n(t),…(xn(t)))T∈Rn为神经元的激活函数,是连续的;w(t)为外部输入.

将递归神经网络(1)作为驱动网络,其响应网络为:

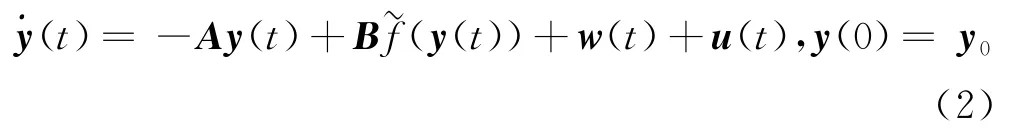
其中:A,B,w(t)在方程(1)中定义;y(t)为响应网络系统的状态向量;u(t)为控制输入.

定义e(t)=y(t)-x(t),则得到如下误差系统的状态方程:

其中:f(e(t))=

因此,递归神经网络(1)和(2)的有限时间同步问题则转化为误差系统(3)的有限时间稳定性问题.

定义1对于驱动网络(1)和响应网络(2),若存在一个常数T*＞0,使得:

并且对于任意t＞T*都有‖yi(t)-xi(t)‖2≡0,则驱动网络(1)和响应网络(2)实现有限时间同步,常数T*为稳定时间.

假设2[15]:对于非周期间歇控制策略,存在0＜ω＜v＜∞,使得

其中,k∈N,tk,sk是时间序列.对于任一时间区间[tk,tk+1],[tk,sk)是控制区间,(sk-tk)为第k个控制宽度;[sk,tk+1)是非控制区间,(tk+1-sk)为第k个非控制宽度.

定义2[15]对于非周期间歇控制策略,定义

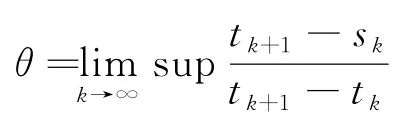
引理1[15]基于假设2,θ≤1-成立.

引理2[16]假设任意向量a1,a2,…,an∈Rn,实数n和0＜p＜2满足

在这个不等式中,当n=1时可以用绝对值表示.

引理3[17]假设V(t)是一个连续可微的正定函数,α0＞0,α1＞0,α2＞0和μ∈(0,1),当t∈[0,∞)时,满足如下条件:

其中,θ在定义2中给出,T*是收敛时间.则可得

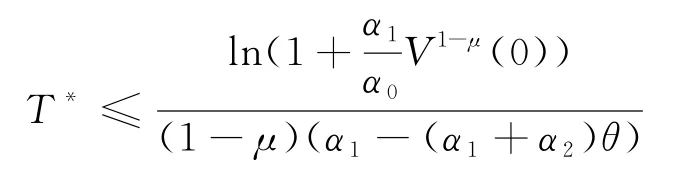
引理4对于事件触发间歇控制,控制瞬间tk和休息瞬间sk由事件触发规则决定,tk和sk如下定义:

其中:V(t)是一个连续可微的正定函数.μ,α1,α2和M0在引理3中定义,∈(0,1),h＞1和ωk∈(0,1)满足:

因此,当以下条件成立时,将触发控制事件

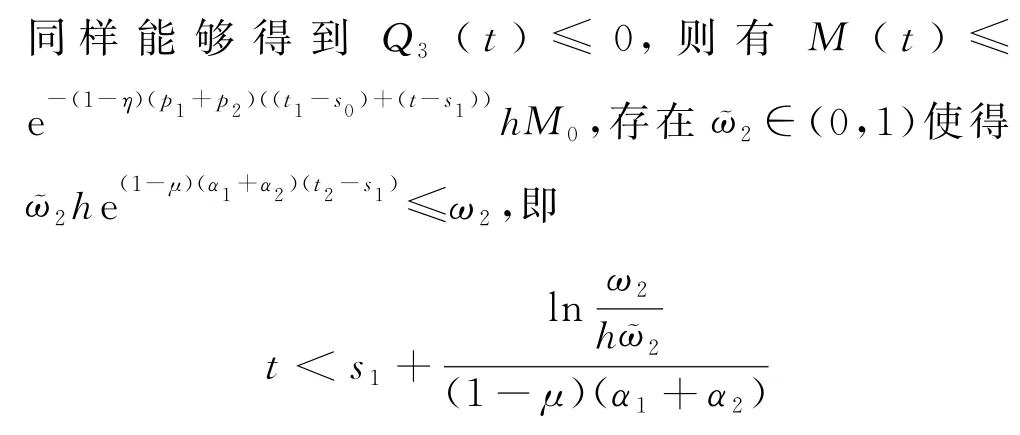
因此,当以下条件成立时,将触发控制事件

根据数学归纳法,可以得到事件触发规则.

证毕.

2 主要结果

设计如下非周期间歇控制器:

其中:l1,l2＞0为控制增益.

将非周期间歇控制器代入误差系统得:

定理1若假设1成立,ξ,β＞0,如果存在正常数α0,α1,α2,d＞0使得下列条件成立:

其中,θ定义在定义2中.

基于事件触发的间歇控制策略,误差系统将在有限时间内稳定,并且Zeno现象没有出现.稳定时间T*满足:

证明考虑下面的Lyapunov函数:

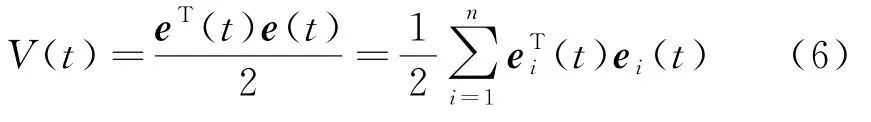
当t∈[tk,sk),k∈N,由式(5)可得式(6)沿误差系统(5)的轨迹对时间t的导数如下:

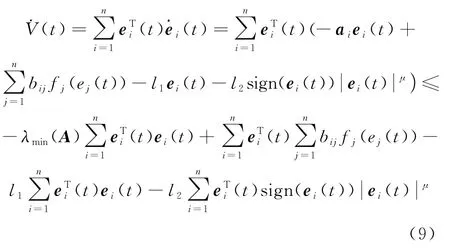
根据假设1,可得:

其中,b=max{bij}.

根据引理2,可得:

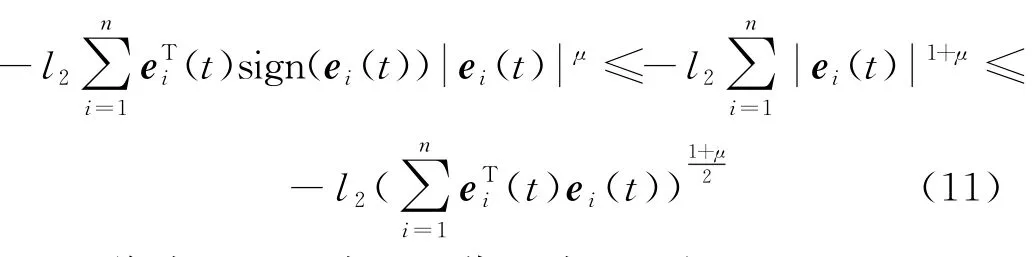
将式(10)和式(11)代入式(9),得:

根据式(12)以及条件(Ⅰ),可得:

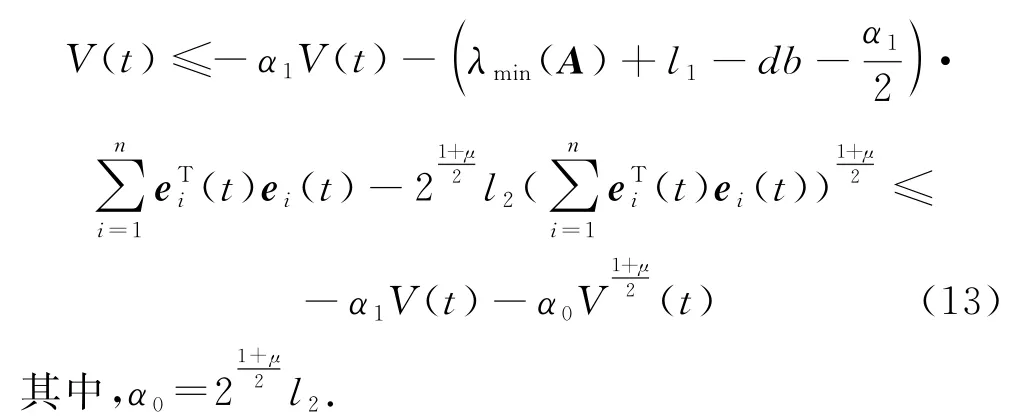
当t∈[sk,tk+1),k∈N,由式(5)可得式(6)沿误差系统(5)的轨迹对时间t的导数如下:

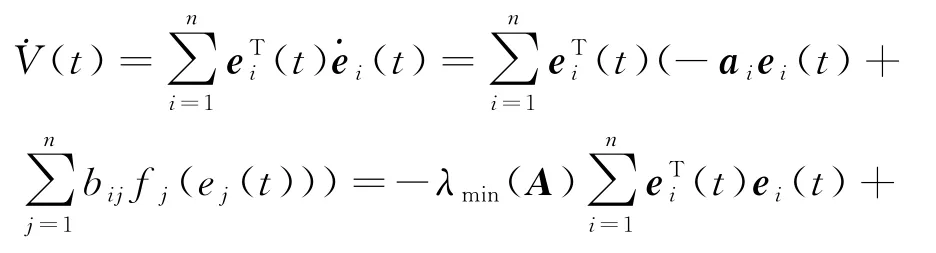
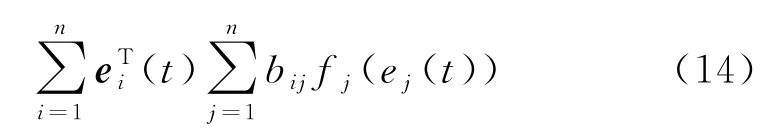
根据式(10),有

根据式(15)以及条件(Ⅱ),可得:

因此,根据引理3,可以得到稳定时间为:

根据引理4中的事件触发规则,对于任何k∈N,当

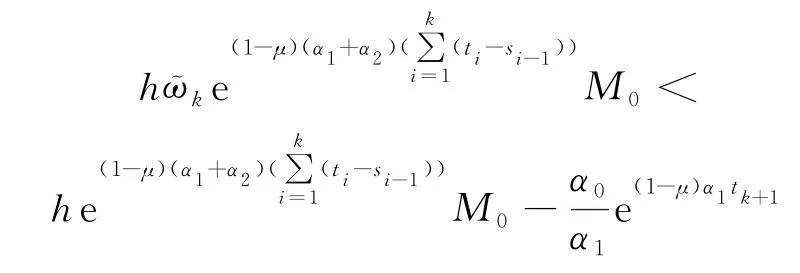
根据条件(Ⅳ),可得:

最后,根据条件(Ⅲ),可得:

即,Zeno行为不可能发生.

证毕.

注1:本文根据事件触发间歇控制实现了一类特殊非线性电路网络系统—递归神经网络的有限时间同步,本文提出的基于有限时间间歇控制方法的事件触发间歇控制策略不同于大多数论文中的事件触发间歇控制[18-19].

3 数值仿真

对于误差系统(3),考虑如下参数:

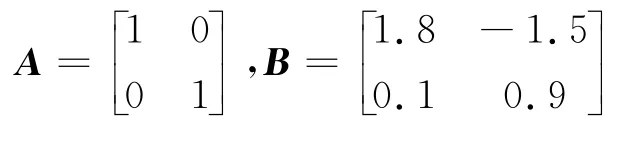
系统(1)的初值为:

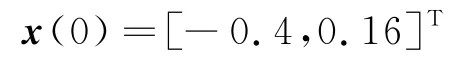
绘出系统(1)的状态变量x1(t)和x2(t)的轨迹图,如图1所示.可以看出,如果不施加控制器,系统(1)是不稳定的.

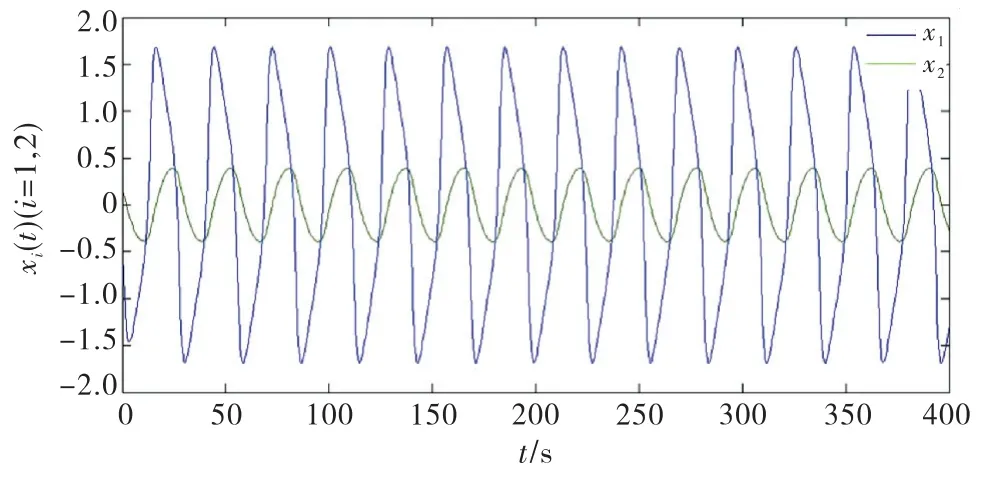
图1 未加入控制器的系统状态时间响应

驱动网络(1)和响应网络(2)的初值分别为:

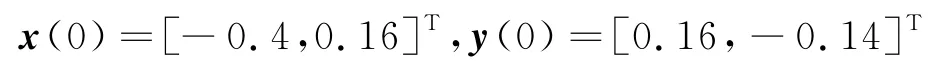
取l1=2.2,l2=1.7660,α0=4.97,α1=2.78,α2=2,μ=,则有

定理1的条件成立,则知驱动系统(1)和其响应系统(2)在控制器(4)下实现有限时间同步.

在控制器(4)下,图2描述了误差系统(3)的轨迹图.从图2可以看出,误差系统的状态变量在有限时间内趋向于零平衡点,即驱动网络(1)和响应网络(2)在有限时间内达到同步.

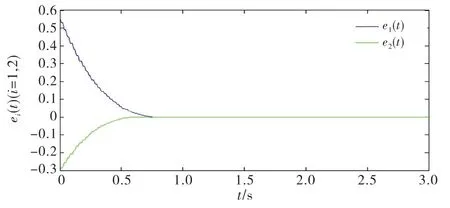
图2 基于事件触发控制器的误差系统时间响应

图3描绘了事件触发瞬间以及间歇控制的控制区间和非控制休息区间,图中的点表示事件触发瞬间.图3的纵坐标值为1时,表示为控制区间,为0时表示非控制区间.

图3 事件触发瞬间以及间歇控制的控制区间和非控制休息区间

4 结论

对于神经网络有限时间同步问题,不少文献已经进行了深入研究.但是,至今还没有人研究事件触发间歇控制的神经网络有限时间同步.因此,本文将事件触发机制引入非周期间歇控制方法,提出事件触发间歇控制方法实现神经网络的有限时间同步.首先,设计了一个间歇控制器,根据有限时间稳定性的证明提出事件触发规则.然后利用Lyapunov 稳定性理论,获得神经网络有限时间同步的充分条件.最后,通过数值仿真验证了结果的有效性.仿真结果表明,在提出的事件触发间歇控制策略下,驱动-响应神经网络系统能够实现有限时间同步.