一种基于标签传播的重叠社区发现算法

贾慧娟，刘 园，史爱静，张霄宏

1(河南理工大学 计算机科学与技术学院，河南 焦作 454003)

2(吉林大学 计算机科学与技术学院，长春 130012)

1 引 言

复杂网络中普遍存在着群集特征.网络中的节点可以形成不同的群组，同一群组内的节点之间关系相对密切，而不同群组的节点间关系相对较弱，称之为“社区结构特性”[1].研究结果表明，网络中的某些节点并不是只属于一个社区，不同的社区在这些节点处发生了重叠[2]，即网络中存在重叠的社区.发现网络中的重叠社区不仅有助于理解网络的功能，还可以帮助人们从用户的行为、群体结构和关系模式中发现复杂网络中隐藏的规律.

有很多方法都可以用来发现重叠社区[3-6]，标签传播算法(Label Propagation Algorithm，LPA)便是其中之一.LPA算法[7]最初用于发现非重叠社区，因具有接近线性的时间复杂度而被广泛关注.Sun等[8]利用优势标签传播来检测重叠社区，利用膨胀算子控制社区之间的重叠率.为了降低标签传播算法在标签更新过程中采用的随机策略导致的社区划分结果不稳定问题[9]，刘世超等[10]引入节点影响力，并按节点影响力由大到小的顺序更新各节点标签.梁世娇等[11]在通过粗聚类得到的社区划分基础上，利用节点亲密度进行重叠社区发现.这些方法都采用了异步的方式更新各节点的标签.与上述方法不同，由Gregory等[12]提出的COPRA算法(Community Overlap Propagation Algorithm，COPRA)采用同步的方式更新标签，即在每轮迭代中仅根据上一轮迭代的标签传播结果来进行本轮的标签更新，本轮中已经更新过标签的节点不对其它节点的标签更新产生影响.COPRA引入了标签归属值以及参数v控制每个节点拥有的标签，在可选标签的归属值都小于1/v的情况下，COPRA仍然采用随机策略选择标签.马健等[13]在COPRA的基础上提出了COPRAPC，该算法利用聚类系数限制每个节点拥有的标签数量.张昌理等[14]的工作也在COPRA的基础上进行，他们采用了异步的标签更新策略，但是按照各节点信息熵的大小顺序对各节点进行标签更新.虽然COPRA采用了同步的标签更新策略，不同的学者也从不同的角度对COPRA进行了改进，但是这些算法中仍然存在随机策略，由随机策略引起的重叠社区划分结果不稳定问题仍然是一个开放问题.

针对COPRA因在标签更新过程采用随机策略而导致的重叠社区划分结果不稳定问题，本文对COPRA进行了改进，提出了COPRA-S算法(Simple Community Overlap Propagation Algorithm).COPRA-S算法采用同步的方式传播标签，且只在以边缘节点为中心的桥梁节点群内进行标签传播，以此提升发现重叠社区的速度.COPRA-S算法还引入了节点连接社区强度，利用其降低标签更新过程中的随机性.此外，引入节点连接社区强度，还可以防止标签的过度传播.

2 COPRA问题分析

COPRA利用标签传播发现重叠社区.该算法采用同步的方式更新标签，引入标签归属值以及参数v控制每个节点拥有的标签.凡是满足条件归属值大于1/v的标签都会指派给节点；如果不存在满足此条件的标签，则随机选择一个标签更新节点，而这种随机选择标签的策略会导致社区划分结果不稳定.

图1所示的例子展示了COPRA存在的社区划分结果不稳定问题.图中节点旁的二元组表示标签与其对节点的归属值.该图给出了相应轮次的迭代后各节点拥有标签的情况.假设在第2轮迭代中，节点的随机遍历次序为v5，v6，v7，v1，v3，v2，v4.由于在v2的邻居节点中出现的标签的归属值都小于1/v，即1/2，故应从这些标签中随机选择一个更新v2，假设选择标签γ.相似的，为v4随机选择标签δ.在这种情况下会得到正确的社区划分结果.但是，如果随机地为v2和v4选择了标签ε，则最终所有的节点都被划分到一个社区.这充分说明了COPRA算法采用的随机策略带来的社区划分结果不稳定问题.

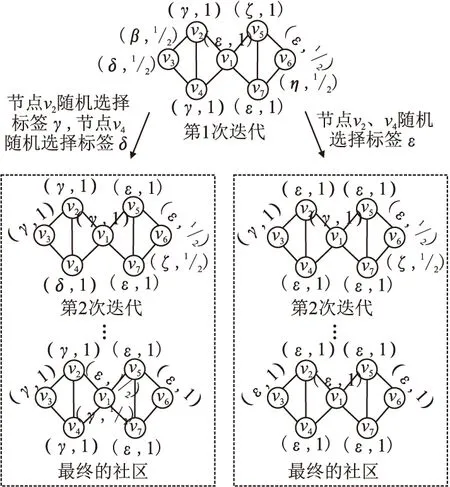
图1 COPRA在v=2时不同的标签更新结果Fig.1 Different label update results of COPRA at v=2

3 COPRA-S算法

为了降低随机性对社区划分结果稳定性的影响，提升算法的性能，本文在COPRA的基础上提出了COPRA-S算法.本节阐述该算法的思想及实现细节.

3.1 算法思想

根据文献[13]的结果，社区内部的节点一般是非重叠节点，而社区边缘的节点由于连接多个不同的社区一般会成为重叠节点.依据这一结果，COPRA-S算法要求即将分析的社交网络要经过预处理划分出非重叠社区，然后在以边缘节点为中心的小范围节点内进行标签传播，并最终发现重叠节点.通过将标签传播限制在以边缘节点为中心的小范围节点内以来提升利用标签传播算法发现重叠节点的速度.在图2所示的网络中，COPRA的标签传播范围包括图中所有节点，而COPRA-S算法只在虚线圈定的节点范围内传播标签.

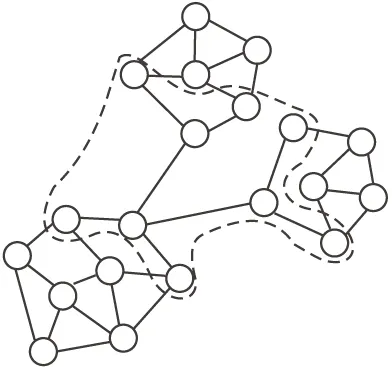
图2 COPRA和COPRA-S两种算法的标签传播范围比较Fig.2 Label propagation comparison of COPRA and COPRA-S

在COPRA中，当某个节点所有邻居节点标签的归属值都小于预设阈值时，随机从这些标签中选择一个更新当前节点，从而导致社区划分结果不稳定.为了降低由随机选取标签引起的社区划分结果不稳定性，在COPRA-S算法中引入一个新的标签选择指标—节点连接社区强度.在所有邻居节点标签的归属值相等且都小于预设阈值情况下，优先采用最大的节点连接社区强度所对应的标签.只有在多个节点连接社区强度对应的标签都满足要求的情况下，才随机选择标签更新节点.

此外，在标签传播过程中引入节点连接社区强度还可以防止标签的过度传播.图3展示了标签的过度传播.在该图中，社区2的标签β经由桥梁节点b3传播到桥梁节点b1.引入节点连接社区强度后，通过设计恰当的节点连接社区强度计算模型和标签传播策略，可以阻止社区2的标签β经由b3继续传到其它社区中的节点.

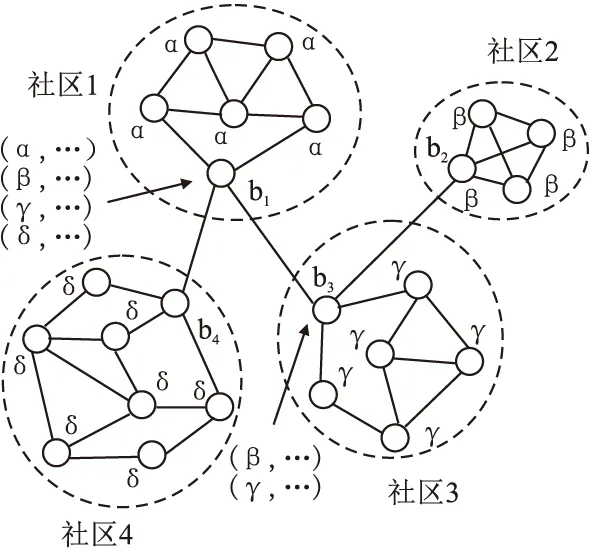
图3 标签的过度传播Fig.3 Excessive spread of labels

3.2 标签传播范围计算

COPRA-S算法的创新点之一是通过在以边缘节点为中心的小范围节点内进行标签传播，来提升利用标签传播算法进行重叠节点发现的速度.为便于划定以边缘节点为中心的标签传播范围，引入桥梁节点、桥梁节点群等概念.

定义1.桥梁节点

∀vi∈V，若vi的标签与某个邻居节点的标签不相同，则vi为桥梁节点.孤立节点不是桥梁节点.

定义2.桥梁节点群

∀vi∈V，若vi是桥梁节点，与vi有边相连的节点共同构成以vi为中心的桥梁节点群，记为Bvi.

桥梁节点连接两个或者多个社区，它们最有可能成为拥有多个标签的重叠节点.但是，重叠节点的标签只能来自于以其为中心的桥梁节点群中的节点.算法1描述了桥梁节点的筛选过程.以某桥梁节点为中心的桥梁节点群则由该桥梁节点及其邻居节点共同构成.

算法1.桥梁节点筛选

输入：G=(V，E)；

输出：Blist；

1.for eachv∈Vdo

2. ifv的邻居节点拥有的标签不完全相同，则

3. 记v为桥梁节点，并加入桥梁节点列表-Blist；

4. end if

5.end for

6.output Blist；

3.3 标签传播

COPRA-S算法采用COPRA算法提出的同步更新节点标签的策略，即本轮标签更新仅受上一轮迭代后的标签更新结果影响，本轮中已经更新的标签只对下一轮的标签更新产生影响.

COPRA-S算法仍然采用归属值作为节点标签更新的重要依据.当桥梁节点群中出现的标签相对于桥梁节点的归属值大于预定义的阈值θ时，将这样的标签指派给桥梁节点，并重新对标签的归属值进行归一化处理，使得桥梁节点拥有的各标签归属值之和为1.

(1)

(2)

(3)

(4)

为了降低标签传播过程中的随机性以及防止标签的过度传播，定义了节点连接社区强度.节点连接社区强度反应节点与社区关系的紧密程度，节点对某个社区的节点连接强度越大，节点和这个社区关系越紧密，节点接受这个社区标签的倾向性就越强，反之亦然.

定义3.节点连接社区强度

节点连接社区强度表示节点连接或归属于某个社区的程度，记为DCon.

∀vi∈V，C为与vi相连的一个社区，vi对社区C的节点连接社区强度记为DCon(vi，C)，可根据式(5)计算.在该式中，Nvi表示vi的邻居节点集合，VC表示社区C中的节点集合.

(5)

COPRA-S算法的详细内容如算法2所示.该算法包含筛选桥梁节点以及标签传播两个阶段.假设网络有n个节点，e条边，每个节点的平均度数为d，筛选桥梁节点的时间复杂度约为O(nd)；影响力计算的时间复杂度是O(et1)，t1为影响力计算过程中的迭代次数；标签传播的时间复杂度约为O(bdt2)，b为桥梁节点的总数，t2为迭代次数.因此COPRA-S算法总的时间复杂度约是O(et1+nd+bdt2).

算法2.COPRA-S算法

输入：已划分好非重叠社区的网络G；

输出：重叠社区划分；

1.t←1；

3.Blist←桥梁节点筛选；

4.for eachvi∈Blistdo

5. 计算Bvi中每个标签相对vi的归属值；

6. 计算vi对于这些标签所属社区的节点连接社区强度；

7. if 存在归属值大于θ的标签

8. 将节点连接社区强度大于0的标签指派给vi；

9. else

10. if 所有标签的归属值都相等

为营造良好的政策环境，双创园先后制定出台促进投资和产业发展、培育绿色企业的产业政策，从培育企业原创技术推广、专利技术产业化、“两化融合”等方面予以重点支持，不断提升企业自主研发水平和原创能力；启动“金豆子”培育工程，力推企业挂牌上市。

11. if节点连接社区强度不等

12. 将最大的节点连接社区强度对应的标签指给vi；

13. else

14. 随机选择一个标签指派给vi；

15. end if

16. else

17. 将归属值最大的标签指派给vi；

18. end if

19.end if

20.end for

21.t←t+1；

22.if传播停止条件未满足

23. 回到步骤4；

24.end if

25.返回标签传播结果.

4 实 验

本文通过在真实网络数据集和人工合成网络数据集上将COPRA-S算法与COPRA、CPM[2]、Demon[16]及CONGA[17]算法进行对比来验证COPRA-S算法的正确性和有效性.展示的所有实验结果均为相关算法独立运行50次的平均结果.

4.1 实验环境及数据集

本文所有的实验均在单台主机上进行.该主机采用了 Intel core i5-7200U 处理器，配置了8GB的内存，并安装了Windows10操作系统.

在实验中既用到了真实网络数据也用到了人工合成网络数据.表1展示了真实数据集的基本信息，其中，前6个数据集来自Newman数据集(1)http：//www-personal.umich.edu/～mejn/netdata/，后3个数据集来自SNAP数据集(2)http：//snap.stanford.edu/data/.

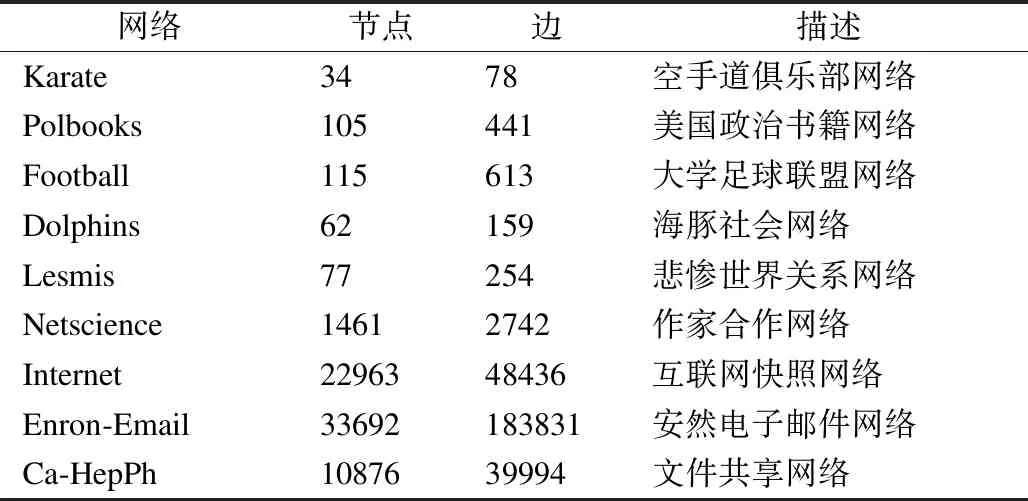
表1 真实网络数据集Table 1 Real network data sets

人工合成网络数据集由LFR基准发生器[18]生成，参数配置如下：节点总数n=5000，平均度数k=50，最大度数maxk=100，社区最小节点数minc=50，最大节点数maxc=100，重叠节点数on=500，每个重叠节点所属的社区个数om=5，mu是混合参数，取值范围从0.1-0.6，以0.1为间隔递增.随着mu的增长，网络结构变得越来越模糊，社区检测的难度也越来越大.

4.2 实验结果及分析

在实验中采用了4个评价指标，分别是重叠模块度-EQ、综合评价指标-F[10]、标准化互信息-NMI以及执行时间，其中，执行时间适用于所有的数据集.由于真实网络数据集中没有重叠社区的真实社区划分，仅采用EQ和F平均值两项指标来评价各算法在真实网络数据集上的表现.在人工合成网络数据集上采用EQ和NMI平均值作为评价指标.此外，COPRA-S算法需要对输入数据进行预处理，即划分非重叠社区，在实验中采用文献[19]中的方法进行非重叠社区划分.

图4展示了各个算法在真实数据集上EQ平均值的比较结果.由图可知，COPRA-S算法在每个数据集上的表现都比COPRA算法要好.其中，COPRA-S算法在Karate、Foot-ball、Netscience、Internet及Enron-Email 4个数据集上的EQ平均值相比于COPRA算法均提高了20%以上.COPRA-S算法在真实数据集上的表现也明显优于其它3个算法.

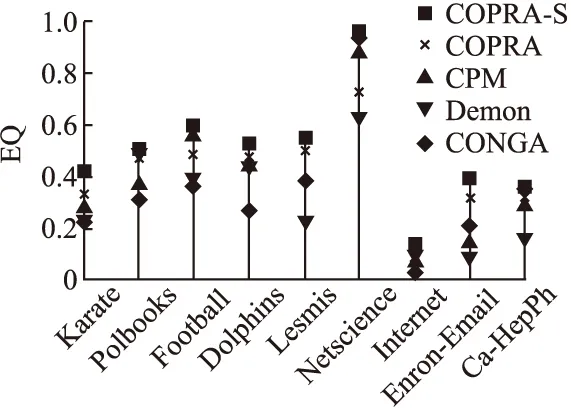
图4 真实数据集上EQ平均值对比Fig.4 Comparisson of average EQ on real data sets

图5展示了各个算法在真实网络数据集上综合评价指标F平均值的比较结果.由图可知，COPRA-S算法在每个数据集上的表现都比COPRA算法要好.其中，COPRA-S算法在Karate、Dolphins、Football、Netscience及Internet 5个数据集上的F平均值相比于COPRA算法均提高了10%及以上.COPRA-S算法在真实网络数据集上的F平均值也明显优于其它3个算法.

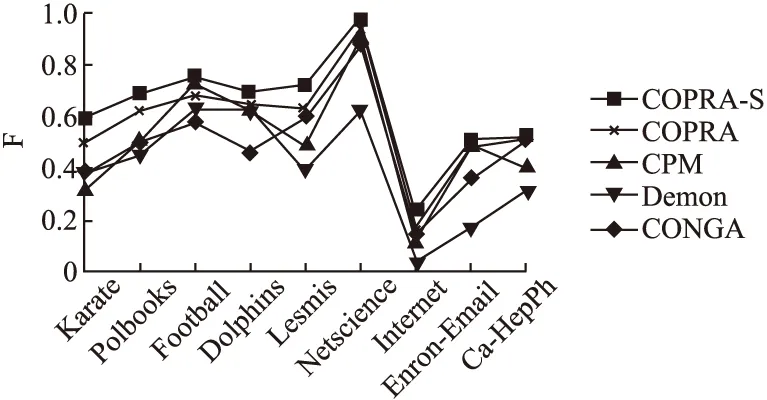
图5 真实数据集上F平均值对比Fig.5 Comparison of average F on real data sets

表2展示了各算法在真实网络数据集上的平均运行时间，时间单位为s.在该表中，COPRA-S算法的执行时间只包括标签传播时间，不包括数据预处理时间，即非重叠社区划分时间.由表可知，COPRA-S算法在各真实数据集上的执行时间明显少于其它算法在这些数据集上的执行时间.

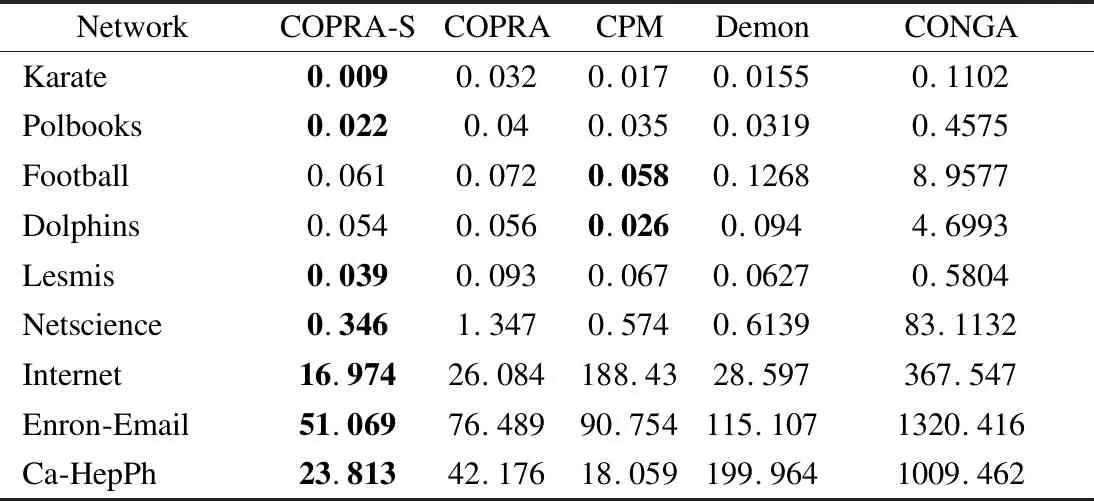
表2 算法在真实数据集上的平均运行时间对比Table 2 Average running time comparison on real data sets

图6展示了各算法在人工数据集上的EQ平均值.从图可知，COPRA-S算法的EQ平均值明显高于COPRA、Demon和GONGA算法.虽然COPRA-S算法在mu为0.2、0.5及0.6时的EQ平均值略低于CPM算法，但是当采用NMI和执行时间这两项指标进行评价时，COPRA-S算法要优于CPM算法.在其他情况下COPRA-S算法所取得的结果都是最好的.

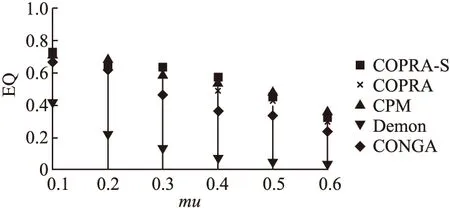
图6 人工数据集上EQ平均值对比Fig.6 Average EQ comparison on artificial datasets

图7展示了各算法在人工数据集上的平均NMI值.由图可知COPRA-S算法的平均NMI值除了在mu=0.3时略低于COPRA外，在其它情况下都大于或等于COPRA.此外，COPRA-S算法的平均NMI值明显高于其他3个算法.综上，COPRA-S算法检测重叠社区的准确性要好于其它算法.

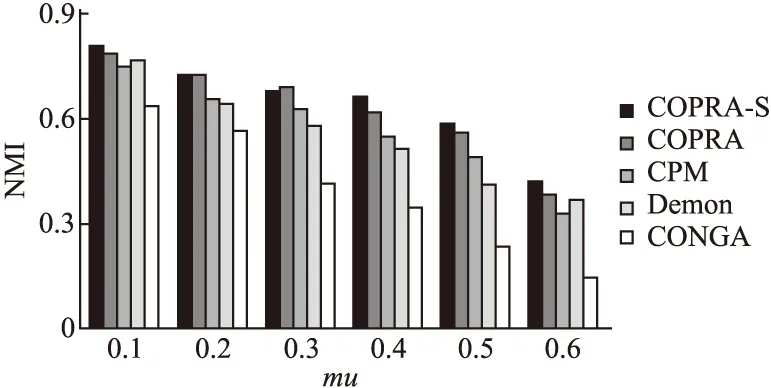
图7 人工数据集上NMI平均值对比Fig.7 Average NMI comparison on artificial datasets

表3展示了各算法在人工生成数据集上的平均运行时间，时间单位为s.在该表中，COPRA-S算法的执行时间只包括标签传播时间，不包括数据预处理时间，即非重叠社区划分时间.由表可知，COPRA-S算法在各人工生成数据集上的执行时间明显少于其它算法在这些数据集上的执行时间.

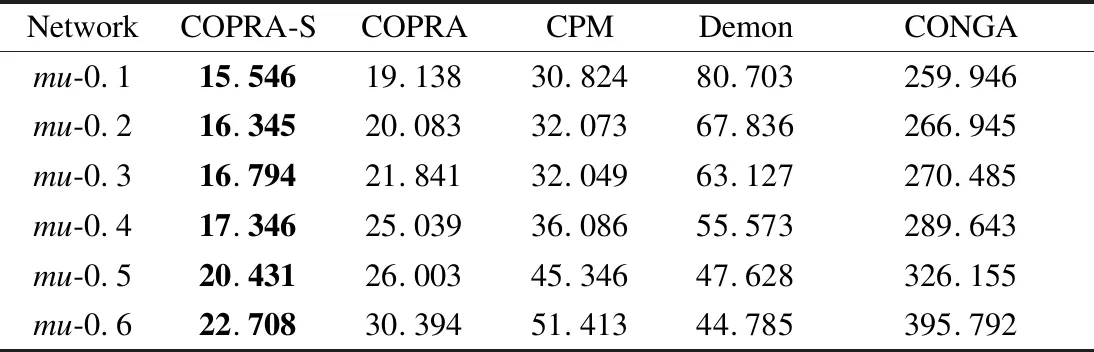
表3 算法在人工数据集上的平均运行时间对比Table 3 Average running time comparison on artificial dataset

5 结束语

本文对COPRA进行了改进并提出了COPRA-S算法.COPRA-S算法采用同步的方式传播标签，且只在以边缘节点为中心的桥梁节点群内进行标签传播，以此提升发现重叠社区的速度.COPRA-S算法还引入了节点连接社区强度，利用其降低标签更新过程中的随机性，并防止标签的过度传播.在9个真实网络数据集和人工合成网络数据集上的实验结果验证了本文方法的正确性和有效性.下一步，将在本文算法的基础上开展动态重叠社区发现方面的研究.