多目标优化视角下在线学习群体形成方法
李浩君,岳 磊,张鹏威,杨 琳
1(浙江工业大学 教育科学与技术学院,杭州 310023)
2(杭州市电子信息职业学校,杭州 310021)
1 引 言
随着互联网的发展以及人工智能、大数据等新兴技术与教育的深度融合,在线学习已成为当今时代的应用新常态.协作学习是在线学习中最有效的学习模式之一,而形成最优在线学习群体是进行协作学习的基础和前提,形成符合教师的教学要求且满足学习者需求的在线学习群体,可以有效改善在线协作学习过程中的学习体验和学习效率.
在线学习群体的形成是在线协作学习领域的重要研究内容,吸引了众多学者对在线学习群体形成开展研究.Abnar[1]、Sun[2]等探讨了在线学习群体形成发展的生命周期;Ho[3]、Zheng[4]等优化了在线学习群体的形成过程;Graf[5]、Yannibelli[6]等研究了影响在线学习群体形成的相关因素等,其主要应用到聚类算法、近似算法、自学习算法等方法,但上述方法存在着噪声敏感、结果不稳定、收敛速度慢、运算量大等缺点.鉴于在线群体形成问题本质上是不同特征人群的组合优化问题;而元启发式算法将随机搜索算法与局部搜索算法相结合,被众多学者认为符合组合优化的求解问题.粒子群算法和遗传算法作为常见的元启发式算法,前者具有参数少、收敛速度快的优势,后者具有编码特征与在线学习群体形成问题参数设置高度吻合的优势,因此将两者应用于在线学习群体形成问题的求解策略中.有学者使用粒子群算法解决分组问题:Matheus等人在粒子群优化算法的基础上,融入了学习者的知识水平和兴趣爱好,以形成大规模在线开放课程的合作小组[7].Lin等人提出了一种改进的粒子群优化算法,不仅可以帮助教师规划不同类型的协作学习过程,而且构建的协作学习组具有良好的结构性[8].Zheng等人以离散粒子群优化算法为基础来构造异构在线学习群体,该算法考虑了性别差异和人格类型的异质性[9].也有学者使用遗传算法解决分组问题:Utomo等人提出了利用遗传算法动态组建学生团体的方法,实证研究表明该方法能够公平地组成项目团队[10].Chen等提出了一种基于遗传算法的惩罚函数组学习群体形成方法,该方法考虑了学生知识水平、学习角色的异质性以及学习组成员之间社会互动的同质性,以生成能够平衡学习特征的协作学习组[11].
上述对学习群体形成问题求解的方法较多采用单目标优化的方式,对个别在线学习群体在优化过程中获得的适应度值控制有限.而在线学习群体形成问题本质上是多目标优化问题,因此采用单目标优化方式求解会存在着难以解决多目标问题复杂性和分组问题全局最优性等局限.因此,近年来有学者尝试从多目标视角进行求解来优化最优在线学习群体的形成过程,Miranda等人基于遗传算法,通过考虑组内同质性、组内异质性和同理心3个方面优化在线群体的形成过程[12].Lin等利用遗传算法和相似度排序技术进行方法改进,以促进多目标学习群体分组的优化[13].Moreno提出一种基于遗传算法的方法来实现同质群体和异质群体,该方法的主要特点是允许考虑尽可能多的学生特征,将分组问题转化为多目标优化问题[14].Garshasbi等人提出了多目标非支配排序遗传算法,该算法能够同时满足预先定义的多个目标,提高最优学习群体形成过程的有效性和准确性[15].目前,多目标优化算法已经成功解决了数字图像水印质量[16]、卫星周期性持续观测[17]、有效产品率提高[18]、通信系统中用户功率优化控制[19]、搜索定位精度[20]等多个领域的多目标优化问题,但采用多目标优化方式对在线学习群体形成方法开展的相关研究仍然较少,是未来在线学习群体形成领域的重要应用研究方向.
针对上述问题,本文首先根据学习者多项特征构建在线学习群体形成模型MOLGFM,学习者特征匹配是形成在线学习群体形成的前提;其次,基于在线学习群体形成模型,设计整合多目标粒子群算法和遗传算法的多目标优化算法GAMOPSO,提出多目标优化视角下在线学习群体形成方法GAMOPSO-FA,从而形成最优在线学习群体;最后,与1种随机方法、1种单目标进化算法、1种经典聚类算法和3种多目标进化算法进行对比分析,验证GAMOPSO-FA方法在在线学习群体形成过程中的可行性与有效性.
2 多目标优化视角下在线学习群体形成模型构建
2.1 问题描述
在线学习群体形成是指根据收集到的在线学习者相关数据,向学习者推荐满足其特征需求的学习群体.多目标优化视角下在线学习群体形成是指将在线学习群体形成问题以多目标问题的形式进行优化求解,从而形成最优在线学习群体.根据已有研究,本文在求解在线学习群体形成问题时考虑的学习者特征有:性别(S)、位置(L)、认知水平(C)、学习风格(M)、学习时间(T)、兴趣偏好(HP)和学习偏好(LP)等.
在分析学习者的学习风格时,依据Kolb的学习风格分类理论,分为聚合型、同化型、发散型、调节型4种[21],表示为M={M1,M2,M3,M4}.在分析学习者的兴趣爱好时,将兴趣爱好分为兴趣偏好和学习偏好两部分[22],表示为HL={HP,LP},其中,兴趣偏好有音乐、财经、科技、旅游、读书、游戏、电影、动漫、体育9类,表示为HP={HP1,HP2,HP3,HP4,HP5,HP6,HP7,HP8,HP9};学习偏好指学习者偏爱使用的学习资源类型,分为视频、图片、文字、音频4类,表示为LP={LP1,LP2,LP3,LP4}.
通过对学习者的特征进行分析,根据其特征采用“组间同质,组内异质”的分组模式.“组间同质”可以使各学习群体公平合理的竞争:“组内异质”可以使学习群体成员合理分工,互帮互助.在整体考虑学习群体互补性和亲密性的基础上,决定以多目标优化为视角,在融合求解后形成最优在线学习群体.
2.2 多目标在线学习群体形成模型构建
基于2.1节中所提出的原则和需求,构建多目标优化视角下在线学习群体形成模型MOLGFM,如图1所示.
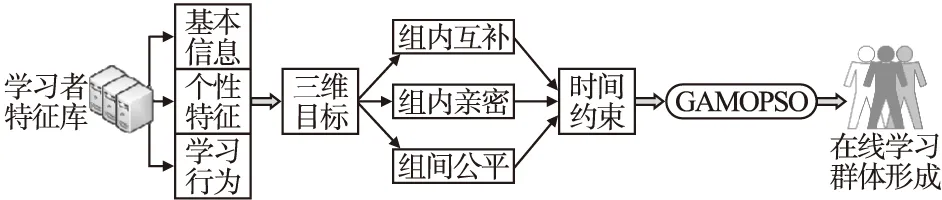
图1 在线学习群体形成模型MOLGFMFig.1 Online learning group formation model MOLGFM
多目标优化视角下在线学习群体形成模型属于三元组结构,包含3个子目标函数,即保证组内互补的学习者特征函数f1、保证组内亲密的学习者特征函数f2以及保证组间公平的学习者特征函数f3,如表达式(1)所示.三者共同决定所形成的在线学习群体能否满足要求.子目标函数f1表示性别、认知水平、学习风格等特征在形成的在线学习群体内部的差异,如表达式(2)所示;子目标函数f2表示兴趣爱好、学习时间、位置等特征在形成的在线学习群体内部的差异,如表达式(3)所示;子目标函数f3表示形成的各在线学习群体间的整体差异,如表达式(4)所示.
minimizeF(x)=(f1,f2,f3)
(1)
f1=(maxMSE(S,C,M))+(minError(S,C,M))
(2)
f2=(minMSE(HL,T,L))+(minError(HL,T,L))
(3)
f3=(minMSE(Gg)|i)+(minError(Gg)|i)
(4)
为了检验在线学习群体形成问题是否是多目标优化问题,同时分析所提出的各子目标函数之间是否存在冲突性.通过随机初始化学习者的各项特征值,然后求解得到3个子目标函数的值及变化状态,最后判断3个子目标函数的最小值所对应的自变量是否为同一个.经检验发现,3个子目标函数不存在在一个解上均达到最优的情况,因此可认为在线学习群体的形成问题是多目标优化问题.然后对各子目标函数的变化状态进行分析,在不同子目标函数上解的变化状态是截然不同的,因此可认为各子目标函数之间是存在冲突性的.
2.3 多目标在线学习群体形成函数设计
首先将X个学习者分成Y组,学习者总群体由数组A表示,具体如表达式(5)所示.
A={A1,A2,A3,…,AX}
(5)
(6)
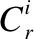
(7)
学习群体形成问题是将定量的学习者分成指定个数的等量在线学习小组,每组学习者数量的个数为:X/Y.在初始学习群体形成后,所有学习者都应用明确的标准进行评估,因此,需要定义相应的适应度函数来对学习者进行更加精确的分组.有学者提出可利用各在线学习群体的各项特征均值与学习者总群体的各项特征均值之差来衡量分组[15].

(8)
(9)
(10)
(11)
表达式(11)在最小化学习群体总误差时并不能保证最小化每组在线学习群体的误差.因此,在解决在线学习群体形成问题时,既要考虑学习群体的总误差,又要考虑各学习群体中的各特征误差.这便需要计算各在线学习群体与学习者总群体的百分比偏差,如式(12)和式(13)用于计算第g组的均方误差和总偏差百分比.
(12)
(13)
3 多目标粒子群优化算法GAMOPSO的提出
3.1 多目标粒子群算法基本框架

(14)
(15)
3.2 多目标粒子群优化算法GAMOPSO设计
3.2.1 粒子进化状态
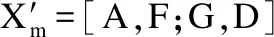

图2 粒子进化状态示意图Fig.2 Schematic diagram of particle evolution state
3.2.2 GAMOPSO算法的伪代码表示
开始
输入:种群规模N、最大迭代次数T
惯性权重ω,认知系数C1,C2,C3
外部档案Archive数量;
for t=1:MaxIt
for m=1:noP
calculate the fitness function;
选择交叉粒子
计算粒子Xm与各粒子之间的距离,选择离Xm远的粒子Xn作为交叉粒子
设定阈值H=0.5
if H<0.5
Delete Xn;
else
Xn→交配池;
end
粒子交叉生成中间粒子
Xm=[A,B;C,D]交叉Xn=[E,F;G,H]

Caculate fitness
else
end
中间粒子变异生成新粒子
将非劣解放入外部档案并维护;
采用轮盘赌策略从外部档案中选择全局最优;
惯性权重ω、个体认知系数C1、社会认知系数C2、探索认知系数C3自适应更新;
达到最大迭代次数;
输出:Pareto Optimality
结束
3.3 GAMOPSO算法在学习群体形成中的应用
在GAMOPSO算法中,将多目标粒子群算法中的粒子赋予遗传算法中染色体的结构.以多目标优化为视角,融合遗传算法和多目标粒子群算法对算法改进设计.在前期依靠GA的交叉变异和全局探索能力以保证种群个体的多样性,提供初步的优化结果,保留全局捜索的优势,在算法运行的后期转为执行MOPSO,强化局部开发,提高收敛速度和计算精度.
3.3.1 编码设置
遗传算法需要将输入特征进行编码,并将其转换为问题潜在解的染色体结构来实现初始化.因此需要设计一个合适的染色体结构来将学习者按预定需求分组为最优学习群体.在定义染色体结构的过程中,还需定义在线学习群体形成的组数和每组学习者数量,且应保持两者均不发生变化,因此本文将定量的学习者聚类到等大的学习群体中.
3.3.2 种群初始化
随机产生初始种群需要预先设定染色体数目.新一代种群通过遗传算子动态调整基因值产生并进化.每个学习者在每次迭代过程中可以通过遗传算子改变其在染色体中的位置,从而形成最优在线学习群体.因此,在种群初始化时,染色体结构中的数字应以随机分布.
3.3.3 适应度函数计算
初始种群产生后,所有染色体粒子都应用适应度函数进行精确评估.基于第2.3节中提出的多目标在线学习群体形成函数求解计算每个学习群体序列在各个目标函数上的适应度值,以此检验形成的在线学习群体是否符合需求.
3.3.4 遗传算子应用
为使形成的在线学习群体序列更好地满足要求,可以应用遗传算子交叉和变异来进行调整.对于最优学习群体形成问题,相关研究者应用了一种顺序交叉算子来产生后代[23],其主要过程是:首先,选择父代1,并随机选择交点,将得到的子字符串直接复制到子代1的相同位置.然后,将选择的父代1基因在父代2中指定.最后,按顺序将父代2中未指定的基因在子代1中的空缺位置进行填补.而在最优学习群体形成过程中,某些基因的随机改变并不能保证新染色体的再现,需要及时处理置换型染色体的突变,交换突变常被用来解决该问题,即一个候选染色体的两个随机基因同时被选择并交换其值,以此产生新的置换型染色体.
3.4 利用GAMOPSO算法优化MOLGFM模型
学习者在进行在线学习时往往具有时间限制,因此应该在保证在线学习群体满足需求的前提下,尽可能缩短形成时间,从而使学习者有更多的时间完成在线协作学习任务.形成的在线学习群体既能保证各学习群体中学习者之间互补,又能确保在线学习群体间学习者之间的亲密度,还能确保各在线学习群体之间的整体水平一致,公平合理的开展组间竞争.本文在MOLGFM模型的基础上,将遗传算法与多目标粒子群算法融合优化形成GAMOPSO算法,并在此基础上提出多目标优化视角下的在线学习群体形成方法GAMOPSO-FA,使其更好地解决在线学习群体的形成问题.模型求解的具体流程如图3所示.
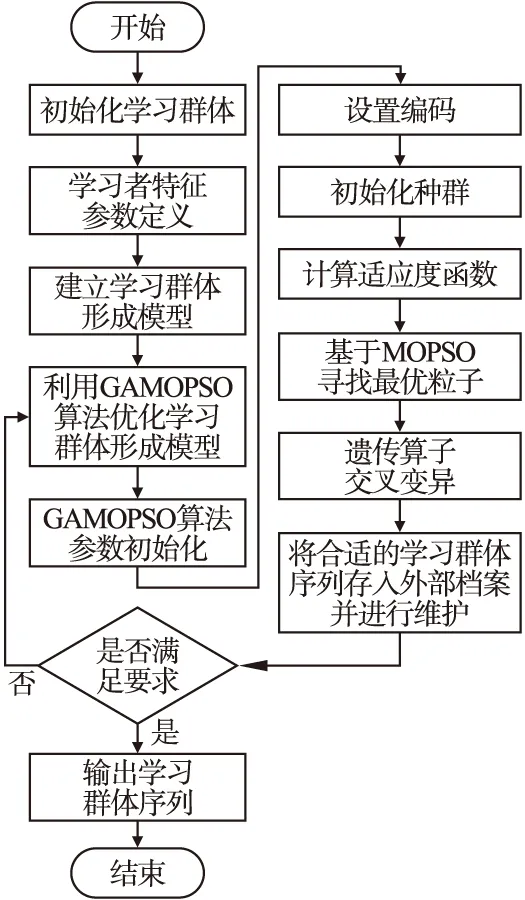
图3 MOLGFM模型求解流程Fig.3 MOLGFM model solving process
特征参数定义是建立多目标优化视角下在线学习群体形成模型的第一步,在2.1节中对模型中的各个参数进行定义.在2.2节中对多目标在线学习群体形成模型的整体框架进行介绍,是否符合所定义的三维目标是在线学习群体能否形成的核心.在2.3节中根据模型对多目标在线学习群体形成函数进行设计.
在使用GAMOPSO算法对在线学习群体形成模型进行求解时,将与在线学习群体形成模型匹配度高的学习群体序列筛选出来,当迭代循环结束时,将其输出.由于学习者分组依靠所形成的学习群体序列,因此外部档案中存储的粒子将直接影响在线学习群体形成的分组结果,也将进一步影响在线协作学习的效率和效果.因此要对外部档案的存储与管理进行维护,设定档案大小为M,当超过M值时便对其进行更新和维护.
4 算法性能及实验结果分析
4.1 实验环境
本文所用编程平台为 Matlab R2018a,硬件环境为intel处理器i5-4200M,操作系统为 windows 7,内存4GB,主频2.50GHz.
4.2 算法性能分析
以MOLGFM模型为核心,利用Huband等人总结的七个测试函数TQ1-TQ7[24]来检验所提GAMOPSO算法的性能.将本文提出的GAMOPSO算法与MOPSO(Multi-objective Particle Swarm Optimization)[25]算法、MOEA/D(Multi-objective Evolutionary Algorithm based on Decomposition)[26]算法、NSGA-III(Nondominated Sorting Genetic Algorithm-III)[27]算法做对比分析,通过收敛性[28]、多样性[29]、成功率[30]、寻优时间和时间复杂度来验证各在线学习群体形成算法的性能.
4.2.1 收敛性分析
逆世代距离IGD[28]是通过计算在真实 Pareto前沿面上的每个点射向算法而获取到的个体集合之间的最小距离和来评价算法的收敛性能,其值越小,算法收敛性能越好.计算公式如式(16)所示:
(16)
其中,P*表示的是均匀分布在真实 Pareto 面上的点集,P表示的是算法在测试函数中搜索到的最优非劣解集,d(v,P)表示个体v到种群P的最小欧式距离,v∈p*, |P*|为分布在真实 pareto面上的点集个体数.
表1是4种算法在7个测试函数上获得的IGD均值和方差.从表中均值数据分析,MOPSO算法仅在测试函数TQ7上获得最优均值,MOEA/D算法和NSGA-III算法均未获得最优均值,而本文所提GAMOPO算法在TQ1至TQ6这6个测试函数上都获得最优均值,说明GAMOPSO算法表现出较好的收敛性.从表1中方差数据分析,NSGA-III算法和MOEA/D算法均未获得最优方差,MOPSO算法在测试函数TQ3和TQ5上获得最优方差,而本文所提GAMOPO算法在测试函数TQ1、TQ2、TQ4、TQ6以及 TQ7上均获得最优方差,说明所提算法GAMOPSO具有良好的稳定性.这是因为GAMOPSO算法将多目标粒子群算法和遗传算法进行融合,解决了种群多样性差,容易陷入局部最优,运行时间长等问题,从而有效提升了GAMOPSO算法的整体优化性能.

表1 4种算法的收敛性指标均值和方差Table 1 Mean and variance of the convergence index of the four algorithms
4.2.2 多样性分析
多样性指标可以用来测量非支配解集的多样性情况,包括不是Pareto最优集合的解集[31],其值越小,算法的多样性越好.计算公式如式(17)所示:
(17)
表2是4种算法在7个测试函数上获得的Delta指标均值和方差.从表2中均值数据分析,MOPSO算法在测试函数TQ2和TQ4上获得最优均值,NSGA-III算法和MOEA/D 算法均未在测试函数上获得最优均值,而本文所提GAMOPSO算法在TQ1、TQ3、TQ5、TQ6和TQ7这4个测试函数上均得到最优均值,说明所提GAMOPSO算法具有较好的多样性.从表中方差数据分析,GAMOPSO算法在测试函数TQ1至TQ3以及TQ5至TQ7上均获得最优方差,具有较好的稳定性.这是因为GAMOPSO算法将遗传算法与多目标粒子群算法相融合,改进了两者各自的不足,突出了两者的结合优势.通过图4的5个二目标测试函数图像可看出GAMOPSO算法在二目标测试函数上均能找到较好的Pareto前沿,且获得的二目标解在Pareto前沿图像上均具有较好的分布,说明GAMOPSO算法的分布性能优于其他3种对比算法.通过图5上的两个三目标测试函数图像可看出,GAMOPSO算法得到的三目标解大部分位于Pareto前沿面上.因此,GAMOPSO算法在7个测试函数中整体表现优异.

表2 4种算法的多样性指标均值和方差Table 2 Mean and variance of the diversity index of the four algorithms
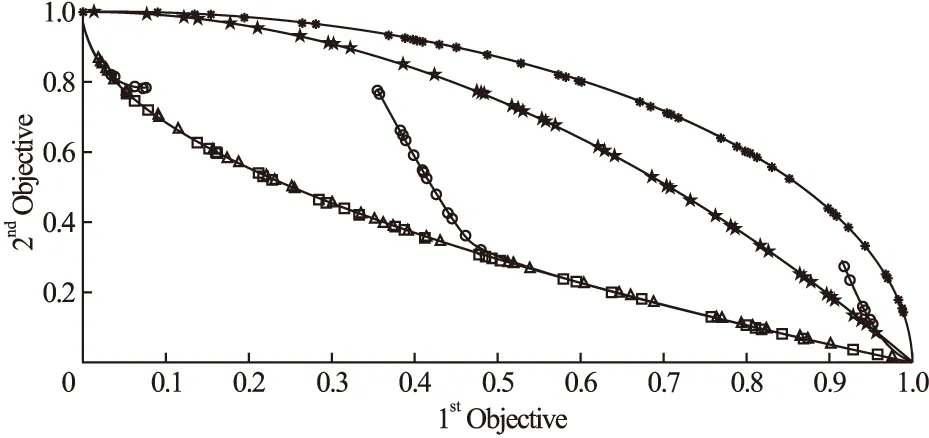
图4 GAMOPSO算法在5个二目标测试函数上解的分布图Fig.4 Distribution diagram of GAMOPSO algorithm on five two-objective test function

图5 GAMOPSO算法在2个三目标测试函数上解的分布图Fig.5 Distribution diagram of GAMOPSO algorithm on two three-objective test function
4.2.3 成功率分析
算法的成功率是指算法寻优精度达到指定精度的次数与总寻优次数之比.本文通过公式(18)计算指定精度AC的数值[28].
(18)
4种算法达到成功率和AC值的次数分别如表3至表6所示,从表中数据分析,GAMOPSO算法在7个测试函数上成功率均为80%以上,且均高于其他3种对比算法.这是因为GAMOPSO算法融合遗传算法和多目标粒子群算法后实现算法全局搜索与局部开采的平衡,因此,GAMOPSO算法获得了较高的成功率.

表3 MOPSO算法的测试结果Table 3 MOPSO algorithm test results
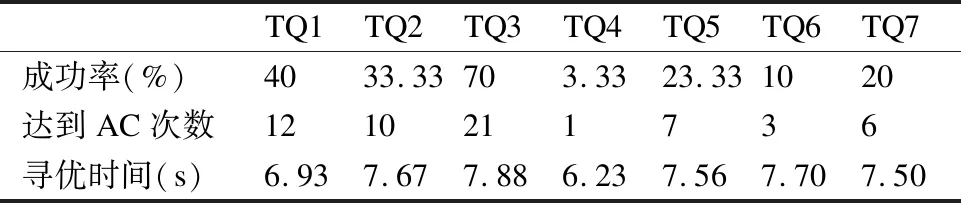
表4 MOEA/D算法的测试结果Table 4 MOEA/D algorithm test results
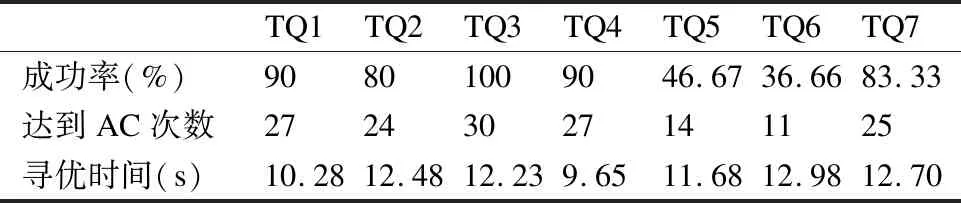
表5 NSGA-III算法的测试结果Table 5 NSGA-III algorithm test results
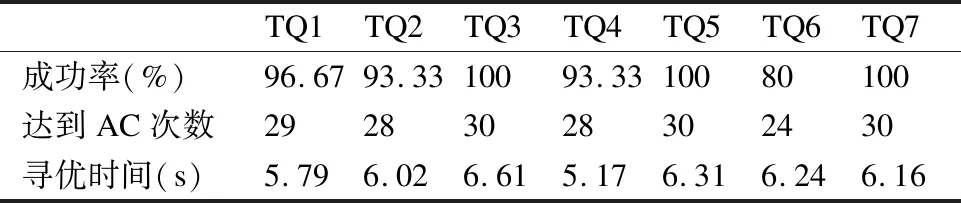
表6 GAMOPSO算法的测试结果Table 6 GAMOPSO algorithm test results
4.2.4 寻优时间分析
算法的寻优时间即运行一次算法求解问题所用的时间.采用不同算法解决在线学习群体形成问题时,既要考虑各个算法形成在线学习群体的匹配性,同时也要考虑各个算法形成在线学习群体所用的时间,以大量时间为代价来提升精度的优化算法方式并非完全可取.因此,可通过寻优时间来进一步分析,表3到表6中呈现了4种算法的寻优时间均值.图6以曲线对比图的形式可以更加直观的显示.从图6可看出,MOPSO算法在测试函数上所用时间最少.由于GAMOPSO算法增加了遗传变异算子,因此所用时间略多于MOPSO算法.
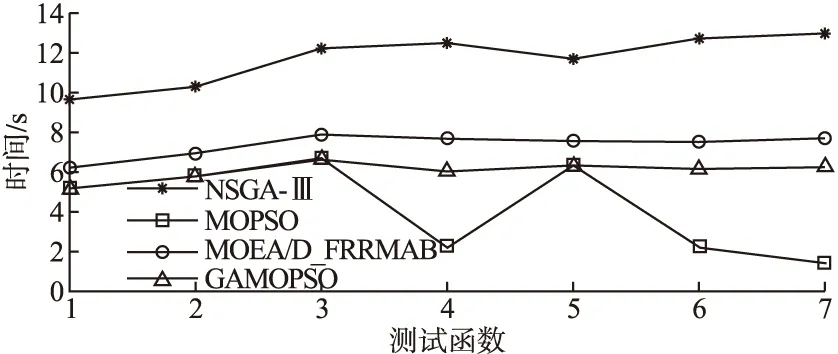
图6 4种算法寻优时间分布图Fig.6 Four algorithms to optimize the time distribution map
4.2.5 时间复杂度分析
设N为群体规模,总目标数为M,外部档案大小为(1/2)*N;GAMOPSO算法循环一次的主要复杂度估计如下:
1)初始生成种群的复杂度为O(MN);
2)粒子适应度计算的复杂度为O(MN);
3)选择交叉粒子的复杂度为O(MN2-MN);
4)生成中间粒子的复杂度为O(N(N-1));
5)中间粒子变异成新粒子复杂度为N;
6)非劣解生成与外部档案维护的复杂度为O(M*(N2/2)).
综上所述,GAMOPSO算法的时间复杂度如表达式(19)所示:
O(MN+MN+MN2-MN+N2-N+N+M*(N2/2))
=O(MN+MN2+N2)=O((M+1)N2)
(19)
根据文献[26-28]可知,MOPSO算法、MOEA/D算法和NSGA-III算法的时间复杂度分别为O(MN2)、O(MTN2)和O(N2logM-2N).MOEA/D算法中的T为邻域大小.由上述分析可知,GAMOPSO算法的复杂度略大于MOPSO算法,但小于MOEA/D算法;说明所提算法的时间复杂度在可接受范围内,GAMOPSO算法在提高性能的同时,并不会以耗费大量的时间为代价.
4.3 实验结果分析
在实验中,将多目标优化算法GAMOPSO构成的GAMOPSO-FA方法与进化算法中的随机方法[32]和单目标PSO-FA方法[33]、传统的K-means聚类算法[34]以及第4.2节中的对比算法MOPSO、MOEA/D和NSGA-III构成的在线学习群体形成方法,从公平性、互补性、亲密性三方面对在线协作学习群体形成结果进行对比分析.由于K-means聚类算法按照欧式距离值进行分类,每次分类数目不一定,即形成的各在线学习群体中人数不一定,为了保证学习群体人数相等,本文根据误差从小到大的顺序,逐个中心点分配固定数目的点,直至数目相等,确保形成的每个在线学习群体中人数相同.
4.3.1 数据集
本实验主要验证所提方法在小规模问题上的优化效果,适合小班化在线协作学习群体的形成.选择一个包含30名学习者(编号为S1-S30)七项特征信息的模拟数据集,主要目标是将学习者分成6个5人学习小组,在满足预定的“组间同质,组内异质”原则的基础上增加组内亲密度、互补度以及组间公平性.基于多目标优化视角下的在线学习群体形成模型,需考虑七项特征的取值范围如表7所示,30名学习者各项特征值如表8所示.
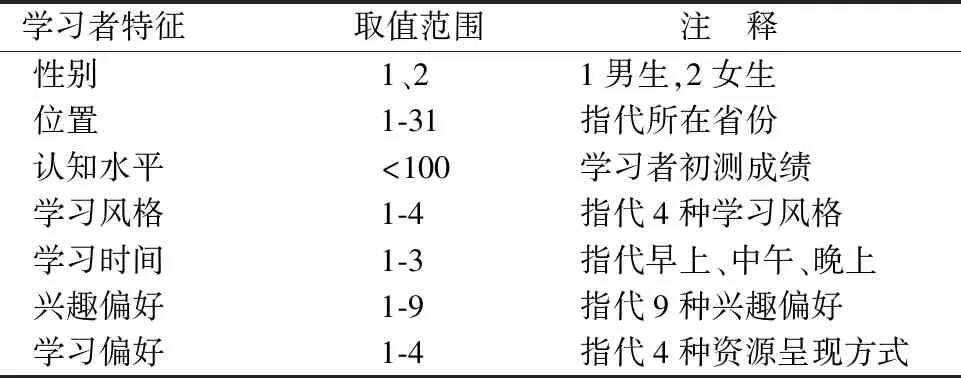
表7 学习者特征的取值范围Table 7 Range of learner characteristics
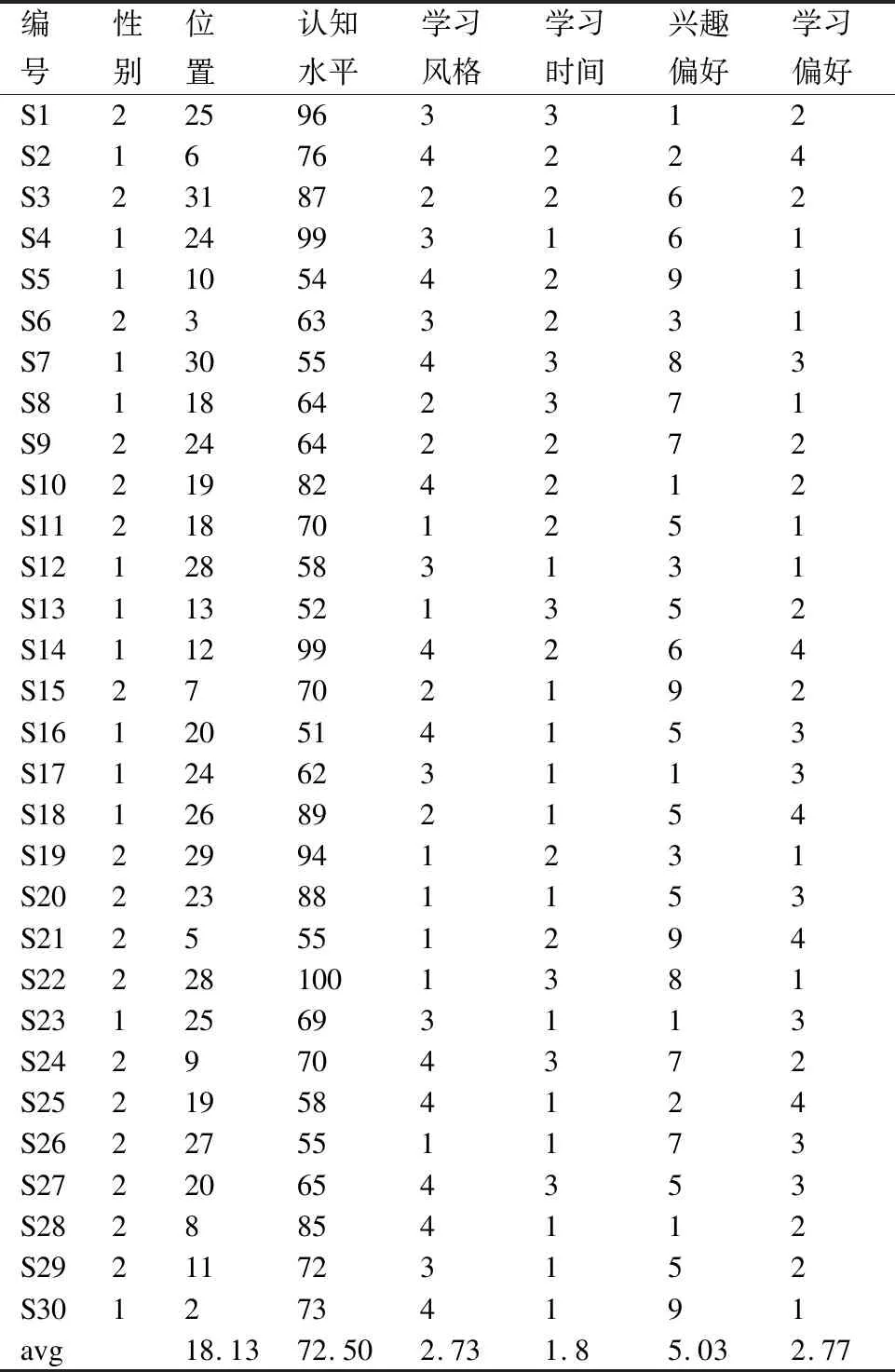
表8 学习者7项特征数据表Table 8 Learner′s seven characteristics data table
4.3.2 实验参数
本文所用到的实验参数设置如表9所示.

表9 所用实验参数表示及取值Table 9 Expression and value of experimental parameters used
4.3.3 评价指标
1)公平性
由于在线协作学习过程中各学习群体间要开展组间竞争,要保障在线协作学习群体的组间公平性,应最大程度的确保各在线学习群体之间彼此相似,形成的各在线学习群体间应保证学习者的各项特征处于相对平衡状态,即所形成的各在线学习群体内学习者特征均值与学习者总体特征均值尽量一致.
2)互补性
为更好的让在线协作学习群体内成员间互帮互助,保证组内异质性,发挥“森林效应”,应将不同认知水平和学习风格的学习者混合分组,实现学习群体成员间特征互补,即形成的在线学习群体内部应包含具有不同特征的学习者,在完成协作学习任务时,各类型学习者的多种思考方式在组内交互碰撞,实现头脑风暴,提高协作学习的效率效果,促进学习者多种能力的培养.
3)亲密性
为解决学习者在学习群体内归属感低的问题,将具有相同兴趣爱好、学习时间等特征的学习者划分到同一小组,不仅能够增加在线学习群体内成员间的互动,提升学习群体内成员间亲密度,而且能够方便教师有针对性的制定教学目标,从而更好凸显协作学习的优势,呈现出在线协作学习的最佳效果.
4.3.4 实验结果
基于随机方法、单目标PSO-FA方法、K-means聚类方法以及多目标粒子群MOPSO-FA(Multi-objective Particle Swarm Optimization-Formation Approach)方法、分解类多目标MOEA/D-FA(Multi-objective Evolutionary Algorithm based on Decomposition-Formation Approach)方法、多目标遗传NSGA-III-FA(Nondominated Sorting Genetic Algorithm-III-Formation Approach)方法和本文所提出的多目标GAMOPSO-FA方法形成的在线学习群体分组结果及各学习群体中各个特征的均值和误差结果如表10至表16所示.

表10 随机方法形成的学习群体结果Table 10 Learning group results generated in a random method

表11 单目标PSO-FA方法形成的学习群体结果Table 11 Learning group results generated by single-target PSO-FA method

表12 K-means聚类方法形成的学习群体结果Table 12 Learning group results generated by K-means clustering method
1)公平性分析
学习群体的组间公平性体现在:学习群体划分后应保障各在线学习群体间学习者的特征均值与学习者的总体特征均值尽量维持一致,即基于性别、认知水平、学习风格特征的各学习群体间没有显著差异,从而确保各学习群体间水平一致.通过表8及表10至表16可知,在性别特征方面,随机方法、单目标PSO-FA方法、K-means聚类方法、多目标粒子群MOPSO-FA方法、多目标遗传NSGA-III-FA方法均出现性别比例1:4或4:1的在线学习群体,分解类多目标MOEA/D-FA方法更是出现性别比例为0:5的在线学习群体,而多目标GAMOPSO-FA方法形成的在线学习群体性别比例均为2:3或3:2,在性别比例方面相对平衡;在认知水平特征方面,随机方法出现83.6、63.4,单目标PSO-FA方法出现79.8,K-means聚类方法出现67.4,多目标粒子群MOPSO-FA方法出现80.4和67.6,分解类多目标MOEA/D-FA方法出现62.8和83.8,多目标遗传NSGA-III-FA方法出现63.6、66.8和89.2等与总体认知水平均值72.5相差较大的在线学习群体,而多目标GAMOPSO-FA方法形成的在线学习群体认知水平均值在总体认知水平均值72.5上下浮动,所形成的在线学习群体在认知水平特征上整体处于相对公平的状态;在学习风格特征方面,随机方法、K-means聚类方法以及多目标遗传NSGA-III-FA方法获得的结果较佳,所形成的各组在线学习群体学习风格均值与总体均值2.73相对接近,而单目标PSO-FA方法、多目标粒子群MOPSO-FA方法、分解类多目标MOEA/D-FA方法、多目标遗传NSGA-III-FA方法及多目标GAMOPSO-FA方法形成的在线学习群体均存在同组中相同学习风格者较多的现象.总体来看,多目标GAMOPSO-FA方法优于其他对比方法,形成的各最优在线学习群体特征值更加接近,具有较高的公平性,能够更好地开展组间竞争.

表13 多目标MOPSO-FA方法形成的学习群体结果Table 13 Result of learning group formed by multi-objective MOPSO-FA method

表14 多目标MOEA/D-FA方法形成的学习群体结果Table 14 Result of learning group formed by multi-objective MOEA/D-FA method

表15 多目标NSGA-III-FA方法形成的学习群体结果Table 15 Results of learning group formed by multi-objective NSGA-III-FA method

表16 多目标GAMOPSO-FA方法形成的学习群体结果Table 16 Learning group results generated by Multi-objective GAMOPSO-FA method
2)互补性分析
学习群体的组内互补性体现在:形成的在线协作学习群体内部成员间在认知水平与学习风格特征上的差异程度.针对认知水平特征,通过表8及表10至表16可知,随机方法形成的第2、4、5组,单目标PSO-FA方法形成的第4、6组,K-means聚类方法形成的第2、3、4组,多目标粒子群MOPSO-FA方法形成的第4组,分解类多目标MOEA/D-FA方法形成的第2、6组,多目标遗传NSGA-III-FA方法形成的1、3、4、5组,学习群体成员之间存在整体认知水平较高或较低的现象,互补性不够突出;而多目标GAMOPSO-FA方法形成的每个在线学习群体内学习者认知水平差异程度相对较大,认知水平高的学习者可以帮助指导认知水平低的学习者,互补性较强.针对学习风格特征,随机方法和K-means聚类方法形成的第6组,多目标粒子群MOPSO-FA方法和多目标遗传NSGA-III-FA方法形成的第1、4组学习群体内仅有两种学习风格的学习者,单目标PSO-FA方法、分解类多目标MOEA/D-FA方法和多目标GAMOPSO-FA方法形成的在线学习群体内均含3种及以上学习风格类型的学习者.总体来看,多目标GAMOPSO-FA方法形成的在线学习群体能够凸显出较强的互补性,有利于更好地集思广益,开拓思路.
3)亲密性分析
学习群体的组内亲密性体现在:形成的在线协作学习群体内部成员间在兴趣偏好、学习偏好、学习时间、位置等特征上的相似程度.通过表8及表10至表16可知,随机方法形成的在线学习群体仅在学习偏好特征上的组内差异性较小,单目标PSO-FA方法、多目标粒子群MOPSO-FA方法、分解类多目标MOEA/D-FA方法形成的在线学习群体仅在学习时间特征上组内差异性较小,K-means聚类方法形成的在线学习群体在学习时间和学习偏好上组内差异性不明显,而多目标GAMOPSO-FA方法形成的在线学习群体在兴趣爱好、学习偏好、学习时间等特征上均表现出较小的组内差异性,具有明显的组间亲密性.以多目标GAMOPSO-FA方法形成的在线学习群体为例,在学习偏好特征方面,第1、2组倾向于文字类学习资源,第3、6组倾向于视频类学习资源,第4组倾向于音频类学习资源,第5组倾向于图片类学习资源;在学习时间方面,第1、2、3、5组均倾向于在上午学习,第4组倾向于在下午学习,第6组倾向于在晚上学习.总体来看,多目标GAMOPSO-FA方法形成的在线学习群体在多个特征上具有组间亲密性,有利于更加顺利的开展完成在线在协作学习任务.
通过上述分析可发现,GAMOPSO-FA方法的各项特征误差值均较低,说明该方法的拟合实验数据能力强,具有较好表现.以多目标GAMOPSO-FA方法形成的在线学习群体不仅优于传统的进化算法,而且也优于基本的聚类算法,说明多目标GAMOPSO-FA方法在在线学习群体形成方面具有较大优势.
5 结论与展望
本文以多目标优化为视角解决在线学习群体形成问题,建立多目标优化视角下在线学习群体形成MOLGFM模型.在总结在线学习群体形成影响因素的基础上,设计融合遗传算法与粒子群算法的多目标优化算法GAMOPSO,提出多目标优化视角下的在线学习群体形成方法GAMOPSO-FA.通过对包含30名学习者特征信息的数据集进行分析,发现GAMOPSO-FA方法能够以较少时间为代价形成具有组间亲密性、组间互补性及组间公平性的最优在线学习群体,证明GAMOPSO-FA方法在在线学习群体形成方面具有良好的性能.未来通过对学习者特征的丰富和完善以及学习者数量的扩大,将进一步验证所提方法的可行性,进而提高形成方法的稳定性和适用性,形成更加合理的在线协作学习群体.

