一种多目标自适应DBSCAN离群点检测算法
黄剑柔,王 茜,蔡星娟,李建伟
(太原科技大学 计算机科学与技术学院,太原 030024)
1 引 言
作为数据挖掘的主要研究内容之一,离群点检测是通过某种特定方法从给定数据集中找出少数和其他多数数据具有显著差别的数据点的一个过程[1,2],这些异常数据可能是错误的数据或者是数据处理过程中引起的误差,也可能是来源于不同的类,它们与正常数据之间存在着显著的差异.离群点检测在很多领域有着非常广泛的应用前景,例如,恶意代码检测[3]、入侵检测[4]、欺诈行为[5]等.传统的离群点检测方法分别是基于统计,基于距离,基于密度和基于聚类进行的.
基于统计的离群点检测方法[6]主要是基于模型进行的,它的主要思想是先为数据创建一个模型,然后对对象进行拟合,最后根据拟合程度来进行评估.对于此方法,数据集的分布情况是十分重要的,需要事先了解,否则错误的估计会导致重尾分布.但是多数情况下,我们都不知道数据的实际分布情况,而且它不适用于高维属性的数据集,因此,在离群点检测中基于统计的离群点检测方法不经常被使用.
基于距离的离群点检测方法主要有效地解决了基于统计的方法不能处理的高维数据集和无法预知数据集分布情况的问题,它主要是通过选取不同的距离度量方式作为离群点的判断方式,其中的代表算法有K近邻(KNN,K-Nearest Neighbor)算法[7],逆K近邻(RKNN,Reverse K-Nearest Neighbor)算法[8]及其它们的改进算法[9].但此方法是针对全局数据集的,不适用于对局部离群数据的检测.
基于密度的离群点检测方法主要适用于分布不均匀的数据集,同时也可以很好解决基于距离的不足.其最具有代表性的算法是由Breuing提出的局部离群因子(LOF,Local Outlier Factor)算法[10],在此基础上,胡彩平提出了DLOF算法[11],将信息熵引入到LOF中用于确定数据的离群属性,并在数据之间距离的求取过程中加入权值,但它在提升离群点检测效率的同时增加了计算量.邹云峰等人提出了LDBO算法[12],该算法在处理数据分布存在异常的离群点检测问题中同时应用了强K近邻点和弱K近邻点,以此对数据进行了区分对待,提高了算法的效率.但是基于密度的离群点检测中带有求解距离的公式,时间复杂度较高,在高维数据中的效果并不是很好.
聚类分析[13]和离群点检测都是数据挖掘中很有研究前景的重要方向,且聚类和离群点检测密切相关,因此,出现了基于聚类的离群点检测方法.其最具代表性的算法有K-means,层次聚类,STING和DBSCAN等.K-means聚类算法[14]的关键在于参数K的选择,首先确定合适的K值,再把每个数据点都划分到离它最近的聚类中心的簇中,最后不属于任何簇的数据点则为离群点.但是K值的不确定性会影响聚类和离群点检测的结果.Chameleon算法[15]是一种经典的动态层次聚类算法,它的核心思想是通过合并来进行聚类,但它和K-means类似,需要预先确定聚类数目K的大小,检测精度不高.STING算法[16]是一种基于划分多层次网格的聚类方法,将数据空间划分为矩形网格,再根据不同的分辨率把矩形网格划分为不同的层次结构,但其网格空间最底层的粒度对聚类和异常检测的精度有很大影响.由于部分常用聚类算法并没有普适性,且算法和数据集之间具有不确定关系,只能针对于特定的数据集使用,如果用于不同的数据集则会导致聚类的效果变差,随之离群点检测的精度也会下降.DBSCAN算法[17]是由Martin Ester等人提出的一种基于密度的聚类算法,提出后在数据挖掘领域受到了广泛关注,主要应用于生物科学、商业营销、社交网络分析和计算机科学等方面,展现出了强大的效果.基于上述DBSCAN的广泛应用和独特优势,本文着重研究了该算法在自适应选择参数配置上的优化改进,解决了最优参数靠经验选择的不足,并针对该算法无法在非均匀数据集上进行有效的离群点检测这一问题进行了深入的研究.
传统基于DBSCAN算法的离群点检测中,两个参数Eps和minPts的设置比较复杂,需要不断进行测试,才能找出用户需求的参数,但这种情况下参数对结果的影响具有很大的敏感性;而且由于数据的密度分布不均匀,密度大的数据点需要一个较大的Eps,密度小的数据点需要一个较小的Eps,统一的全局Eps会淹没部分离群点.且近些年来,多目标优化算法也是研究的重点.因此,为了避免人为设置参数的困难和误差,本文提出一种新的基于NSGA-II算法的自适应DBSCAN离群点检测方法.首先,使用DBSCAN来找出原始数据集中的有可能为离群点的数据子集,其中原始数据集中的每个数据点可以采用不同的Eps,而这个Eps是通过多目标优化算法NSGA-II求解得到的,不但可以避免人为设定参数问题,而且可以反映出数据集本身的特征.其次,使用基于Eps的LOF算法计算筛选后数据子集中各数据的离群得分,减少了计算量.最后,使用UCI不同数据集来进行实验,验证了本文算法的正确性和有效性.
2 问题描述与模型介绍
对于离群点检测这一重要问题,本文主要是通过使用NSGA-II优化的自适应DBSCAN算法从原始数据集中筛选出最有可能为离群点的部分数据,再使用基于Eps的LOF算法对筛选出的数据进行计算,以此找到最终的离群点.
2.1 改进的DBSCAN
DBSCAN通过参数(Eps,minPts)分析数据样本分布程度的大小.其中Eps表示的是距离阈值,也就是以某一数据样本为中心,以Eps大小为半径的邻域.minPts是以某一数据样本为中心,Eps邻域范围内数据点的个数,DBSCAN中通常将其作为密度阀值来计算.传统的基于DBSCAN检测离群点方法的主要思想是将数据集聚类之后,没有被划分到任何簇的数据点为离群点.但是传统DBSCAN算法通常采用人为经验设定的参数作为全局统一参数,这就会导致在非均匀密度数据集中的一些离群点的聚类簇归属出现错误,且通过该方法检测的离群点会随着参数Eps和minPts的变化而发生改变,这无法反应真实有效的离群点分布情况.因此,我们通过改进DBSCAN算法人为手动设置参数和全局设置统一参数来有效避免部分数据被错误划分的情况,从而能够提高离群点检测的准确度.改进的DBSCAN和传统的DBSCAN算法示意图如图1(a)、图1(b)所示.

图1 DBSCAN与改进的DBSCAN原理示意图Fig.1 Principle diagrams of DBSCAN and the improved DBSCAN
图1(a)为传统的DBSCAN给每个数据点设置相同的半径,对于密度分布不均匀的数据会降低检测效率;图1(b)图是本文改进的DBSCAN,它会根据数据的分布情况自适应调节半径Eps的大小,更能体现出数据本身的分布.
改进的自适应调节Eps参数的DBSCAN算法的伪代码如算法1所示.
算法1.改进的DBSCAN
输入:数据集D,minPts,Eps(不同的数据设置不一样的Eps,本文数据集中各数据的Eps由优化算法NSGA-II求解)
输出:离群点数据集
过程:标记所有对象为未访问;
创建新的簇C,创建离群点集合Q;
从任意一点p开始,并进行标记;
If p的领域内至少有minPts 个数据点
P加入到簇C;
令N为p的邻域内的对象集合;
For N中的各个数据
If q未标记
对q进行标记;
判断其Eps邻域内的数据个数是否大于minPts;
If q的领域内至少有minPts 个数据点
q加入到簇C;
q的邻域加入N;
else
q为离群点,加入离群集Q;
End
End
else
标记P为离群点,并加入离群集Q;
End
2.2 基于NSGA-II算法的多目标模型
在本文中,我们使用NSGA-II多目标优化算法为数据集中的每个数据点求解一个最优的Eps,在该模型中,算法为数据集中的各个点随机初始化一组Eps解,随后的迭代过程中经过选择交叉变异进行更新,以此寻找最优解,我们具体的多目标Eps优化模型如下所示:
目标1.我们定义DBSCAN算法中minPts与Eps的比值来测量离群度,minPts与Eps的比值越小,表示数据的离群度越高,因为在离群数据的周围,数据分布是比较稀疏的.
(1)
目标2.在利用DBSCAN算法检测离群点时,半径Eps内的点到簇类中心的距离越远则越可能是离群点.
(2)
(3)
在这里,distance(Pi,Ci)表示Pi到簇类中心Ci的距离,距离越大表示数据Pi离Ci越远,属于Ci的程度越低,越可能是离群点.
因此,本文综合考虑以上两个目标,将该问题形象描述为:
min[F1,F2]
(4)
约束条件如下:
Eps(i) (5) 在这里,r是指包含所有数据点的最大半径,如果Eps过大则失去了聚类和离群检测的意义.公式(5)表明Eps最大不能大于包含所有的数据点的半径. LOF是一种基于密度的离群点检测方法,其主要是通过比较每个数据点和其邻域数据点的密度大小来判断该数据点是否为异常点,密度低的数据点则可能被识别为异常点.由于LOF主要是通过数据的K距离来计算距离,因此本文算法的K距离使用DBSCAN优化出的Eps来代替,减少了算法的时间复杂度. NSGA-II是一种改进经典NSGA的多目标优化算法,它适合应用于复杂的、多目标优化问题,其主要通过改进NSGA的不足,增加了选择压力,提高了搜索速度.NSGA具有较高的算法时间复杂度,特别是在种群规模较大时,非支配排序速度会变得很慢,NSGA-II采用了带有精英选择策略的快速非支配排序,在减小排序时间复杂度的同时还保证了算法的收敛性.精英选择策略保留上一代种群中的最优个体,加强了搜索能力.在种群多样性方面,NSGA使用共享函数来保证解的均匀分布,但是共享函数的方法在保证种群多样性的方面常常依赖于共享参数的选择;种群中的个体之间需要相互比较,共享函数的复杂度较高,而NSGA-II重新定义了拥挤距离来代替共享参数. 基于NSGA-II的DBSCAN离群点检测伪代码如算法2所示. 算法2.基于NSGA-II的DBSCAN离群点检测 开始 输入:数据集D,交叉算子(Pc),变异算子(Pm),最大迭代次数(Gmax),minPts. 初始化:根据公式(1)和公式(2)计算目标值; 快速非支配排序; 选择,交叉,变异; 迭代次数(Gen)= 1; While Gen < Gmax do 结合子代和父代种群; 根据公式(1)和公式(2)计算目标函数值; 快速非支配排序; 选择操作; If rand() 交叉操作; End If rand() 变异操作; End Gen = Gen +1; End 求解得到数据集中各个数据点对应的Eps; 根据算法1改进的DBSCAN,筛选出离群点集合; 对于DBSCAN筛选出的离群点集,使用LOF计算每个数据点的离群得分,在LOF中,我们要求K距离和相应数据的Eps保持一致; 输出:离群点集合. 结束 利用NSGA-II改进DBSCAN算法的具体介绍如下: 1)对于DBSCAN中每个数据点的Eps的求解,我们采用实数编码方法,假设输入数据集中数据点的个数为N,则随机产生规模为N的初始种群POP,本文的种群是:{x1,x2,x3,…,xN},分别对应使用DBSCAN检测离群点时输入数据集中每个数据对应的半径参数Eps.这里选择方式使用二元锦标赛方法,即对POP中个体进行快速非支配排序和拥挤距离比较产生父代种群P. 快速非支配排序结果中的排序值越小,说明它被剩下其他个体支配的次数就越小,有着越大的概率被选择.拥挤距离的计算方法为该个体与其相邻的两个个体形成的矩形的长宽和.在排序值相同的情况下,要保留拥挤距离更大的个体. 2)通过交叉、变异操作得到子代种群Q,并将父代种群P与子代种群Q合并为一个新的种群R. 交叉:交叉是为了使父代的优良基因可以遗传给子代,本文采用模拟二进制交叉方法(SBX),交叉分布指数设置为1,其原理图如图2所示:P1和P2为父代,Q1和Q2为子代,在交叉点处进行标记,交换两个父代交叉点之后的基因片段,得到新的两个子代. 图2 交叉原理图Fig.2 Cross instance 变异:变异是为了改善算法的局部搜索能力,维持种群的多样性.它是以一定的概率进行的,此处设置为0.1.本文变异原理图如图3所示:在子代中以变异概率找出两处基因变异位,然后交换其基因,以此生成新的子代. 图3 变异原理图Fig.3 Variation instance 3)利用精英策略产生下一代群体.其主要是采用快速非支配排序策略对R中的个体进行排序,且在每个非支配层中,对个体进行拥挤度的计算,根据计算得出的非支配关系和个体拥挤度联合选取最优的个体构成下一代种群. 本文所有实验均是在Matlab R2018a版本上实验的,且为了验证本文模型和算法的有效性,我们设置了两组实验:一是本文所提模型在不同数据集之间的对比;二是不同离群点检测算法的对比,对比算法包括:LOF,K近邻,DBSCAN.此外,本文涉及到的参数设置如表1所示. 表1 参数设置Table 1 Parameter setting 为了验证本文算法对于多种形态数据集的普适性,本文使用了UCI数据集中的不同数据集. 对于UCI数据集,由于预先知道测试数据集中的每个对象所属于的真正类,所以将数据集中小类中的对象定义为异常数据对象.对于小类对象中数据较多的,本文从小类中随机选取出少数点作为离群数据.本文实验中使用的UCI数据集如表2所示. 表2 UCI数据集Table 2 UCI data set 采用以下的准确率对算法的离群精度进行评价: (6) 在这里,precision表示检测出的离群点和原始数据中离群点个数的比值,N2为检测出的离群点总数,N1为检测出的正确的离群点个数.准确度越高,表示所提算法越有效. 4.3.1 算法结果分析 本文的离群点检测方法主要分为两个步骤,先选取一个离群子集,再进行离群点确定.经过大量的仿真实验,不同数据集下的实验结果如表3所示. 表3 本文方法检测离群点结果Table 3 Outlier detection results 从表3可以看出:对于iris和zoo数据集,在第1步得到的离群点子集中便包括了全部离群点,第2步的计算可以精确的选择出所有离群点;对于yeast数据集中,在第1步得到的离群点子集中,缺失了一个离群点,第2步检测出了离群点子集中的全部离群点;对于wine数据集,算法的第1步可以得到所有离群点,在第2步缺失了一个;但是整体来看,本文算法在第1步筛选出的离群点子集几乎会包含所有的离群点,再通过第2步的基于Eps参数的LOF算法进行检测,具有很高的离群点检测效率. 4.3.2 离群点检测算法对比 为了对离群检测算法的准确率进行评估,在UCI数据集上采用不同离群点算法(LOF,K近邻,DBSCAN)进行了实验对比.为了减少人为设置参数带来的实验误差,本文取了不同参数下30次实验的平均值,具体实验结果如表4和图3所示. 表4 不同算法准确率对比Table 4 Comparison of accuracy of different algorithms 由表4可以得出,对于不同的数据集,不同的离群点检测方法具有不同的精确率.对于iris数据集,本文算法的准确率达到了0.9943,LOF次之,DBSCAN效果最差;对于yeast数据集,LOF略高于本文算法,K近邻算法最差;对于wine和zoo数据集,可以得出相同的结论.整体来说,相对于其他3种算法,本文算法具有较优的性能. 为了更直观的分析实验结果,对不同算法的离群点检测结果做了柱状图.从图4依旧可看出,本文算法具有最高的离群点检测准确率,LOF的准确率较低,而K近邻和DBSCAN的准确率最低. 图4 准确率变化趋势柱状图Fig.4 Histogram of variation trend of accuracy 本文针对DBSCAN离群点检测算法中全局参数Eps的不确定问题,通过构建多目标模型,使用多目标优化算法NSGA-II对数据集中每个数据对应的Eps进行优化求解,以此选取出离群点子集;其次,再对由上一步选取出的离群点子集进行LOF计算,在LOF中,我们使用相应数据的Eps代替其k距离,也避免了k距离的选择问题.最后,通过仿真实验证明了多目标模型的合理性和算法在不同数据集下的有效性. 在未来的工作中,我们将考虑DBSCAN算法中的另一个参数minPts的自适应选择问题,通过自适应的确定DBSCAN算法中的两个参数,提高高维数据的聚类效果和离群点检测效率.另外,我们还可以考虑建设高维多目标模型,对参数进行优化求解.2.3 LOF
3 算法介绍
3.1 算法基本思想
3.2 算法具体实现


4 仿真实验及结果分析
4.1 参数与环境

4.2 数据集

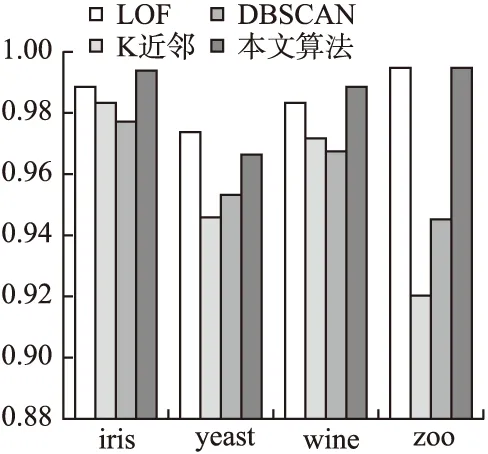
4.3 实验分析


5 结 论

