Sensitivity of Lake-Effect Convection to the Lake Surface Temperature over Poyang Lake in China

Haibo ZOU, Shanshan WU, and Jiusheng SHAN

1 Key Laboratory of Poyang Lake Wetland and Watershed Research of Ministry of Education & School of Geography and Environmental Science,Jiangxi Normal University, Nanchang 330022

2 Meteorological Sciences Institute of Jiangxi Province, Nanchang 330046

3 Key Laboratory of Natural Disaster Monitoring, Early Warning and Assessment of Jiangxi Province, Nanchang 330022

4 Jiangxi Climate Center, Nanchang 330046

ABSTRACT In this study, high-resolution weather research and forecasting (WRF) simulations are used to explore the sensitivity of lake-effect convection over Poyang Lake (PL) to the change of lake surface temperature (LST). A control experiment (CTR) with climate mean LST (303 K) is compared with six sensitivity experiments (CTR-1/2/3K and CTR+1/2/3K) in which the LSTs are set based on the mean LST difference of 6 K between the maximum and minimum. The results show that the CTR experiment reasonably reproduces the lake-effect convection, and the lake-effect convection in sensitivity experiments is significantly influenced by the LST. With the increase of LST, the initiation time of the lake-effect convection is advanced gradually, while the initiation location moves PL from its shore.The lake-effect convection strengthens (weakens) in the increase-temperature CTR+1/2/3K (decrease-temperature CTR-1/2/3K) experiments, but the lake-effect convection does not monotonically strengthen with the LST, for the strongest one occurring in the CTR+1K experiment. The corresponding diagnostic analysis shows that the upward sensible heat flux and latent heat flux over PL increase with the LST, resulting in the enhancement of the lake–land breeze and the enlargement of the convective available potential energy (CAPE). This is the main reason for the changes in the initiation time and location, as well as the intensity of lake-effect convection in different experiments.In addition, the non-monotonous variation of the level of free convection, which is mainly induced by the non-monotonous variation of the lifting condensation level, is responsible for the non-monotonous variation of the lake-effect convection intensity with the LST.

Key words: Poyang Lake, lake-effect convection, lake breeze, convective available potential energy (CAPE), level of free convection (LFC)

1. Introduction

Compared to the surrounding land or vegetation surface, lake is an important moisture source for low-level atmosphere, and is characterized by unique physical properties, i.e., low albedo, small surface roughness, and high thermal inertia (Wu et al., 2019). These unique physical properties can directly alter the surface thermal conditions and the water and energy balances (Nordbo et al., 2011; Ma et al., 2014; Stepanenko et al., 2014), affecting the weather over the lake region. Early in the 1950s, Wiggin (1950) pioneered that under the low-level cold advection, the Great Lakes (area more than 10,000 km2) in North America can induce convection (precipitation) over these lakes and their surrounding areas. Such convection or precipitation is well-known as lake-effect convection or precipitation. After that, the lake-effect convection of the Great Lakes in North America has been widely concerned, and its forecasting skill, climate characteristics, formation mechanism, and numerical simulations have been deeply investigated (Holroyd, 1971;Hjelmfelt, 1990; Kristovich and Spinar, 2005).

Recently, with the operational application of new generation Doppler weather radar, the ability of monitoring convective weather has been significantly improved.Some small- and mid-size lakes, with an area less than 5000 km2or even 1000 km2, have been documented that they can also produce lake-effect convection, for example, the Great Salt Lake with ~3800 km2(Steenburgh et al., 2000; Alcott et al., 2012), Champlain Lake with~1200 km2(Laird et al., 2009), Finger Lake with ~1000 km2(Laird et al., 2010), and Tahoe and Pyramid Lakes with less than 500 km2(Laird et al., 2016) in North America. Moreover, the Taihu Lake with ~2400 km2,Nam Co Lake with ~1920 km2over the Tibetan Plateau,and the lake clusters over the Tibetan Plateau in China can also affect the regional convective precipitation (Gu et al., 2016; Dai et al., 2018; Wu et al., 2019). More importantly, the Poyang Lake (PL), which is the biggest freshwater lake in China with ~3800 km2, can affect crossing convective storm (Fu et al., 2013; Zou et al.,2020) and produce lake-effect convection (Zou, 2020).

Lake surface temperature (LST) not only indicates the amount of energy available in a lake that can be transferred to the lowest layers of the atmosphere, but also determines the saturated vapor pressure of the overlying air mass (Carpenter, 1993). Clearly, the LST has obvious influences on the exchanges of heat and water vapor between a lake and the overlying air (Kristovich and Laird, 1998), and can modulate the atmospheric stability and near-surface wind over the lake region (Steenburgh et al., 2000; Kristovich et al., 2003; Zou et al., 2020). As a result, the LST plays an important role in producing the lake-effect convection or affecting the crossing storm(Carpenter, 1993; Miner and Fritsch, 1997; Kristovich et al., 2003; Laird et al., 2010; Metz, 2011; Zou et al.,2020). The temperature difference between the lake surface and 850/700 hPa has become a key index to forecast the lake-effect convection over the Great Lakes in North America (Byrd et al., 1991; Niziol et al., 1995),and the temperature difference between the lake surface and the surrounding land surface has also been regarded as an important factor to produce the lake-effect convection over the Great Salt Lake in North America (Steenburgh et al., 2000).

Since the LST can obviously affect the lake-effect convection or crossing precipitation system, its accurate estimation has become an important task to improve the skill of regional scale numerical weather forecast (Balsamo et al., 2012; Zhao et al., 2012; Wright et al., 2013).The impacts of LST on the local precipitation have also been discussed by using numerical models. For example,Wright et al. (2013) indicated that an increase of LST resulted in an expansion of the precipitation (snowfall)area both along and downwind to the shore of Great Lakes in North America. Sun et al. (2015) pointed out that the intensification (weakening) of precipitation over the Lake Victoria Basin in the eastern African Plateau occurs with the increase (decrease) of LST.

However, there are few studies discussing the impacts of LST on the lake-effect convection over PL in China.Therefore, in this study, we will focus on a specific lakeeffect convection event that occurred on 12–13 August 2015, and employ the high-resolution weather research and forecasting (WRF) model to investigate how the LST affects the lake-effect convection and the related physical explanations. The remainder of this paper is organized as follows. Section 2 presents an overview of the PL and data, and Sections 3 and 4 exhibit our selected case and model setup, respectively. Section 5 represents the simulation results, and Section 6 describes the corresponding discussion. Conclusions are given in Section 7.

2. Overview of Poyang Lake and data

2.1 Poyang Lake and its surrounding topography

PL, the biggest freshwater lake in China, is in the north of Jiangxi Province and to the south bank of the Yangtze River. PL is a seasonal variation lake, and its area varies with rainfall. In summer, PL occupies a water coverage of about 3800 km2, with the south–north length of about 130 km, the west–east average width of about 30 km (Fig. 1), and the mean depth of about 5.1 m(Wang et al., 2016; Zou et al., 2020). Several steeply sloped mountains with the altitude exceeding 300 m located to the west, northwest, north, and northeast of PL,for example, the Mufu Mountains, the Meiling, and the famous Lushan (Fig. 1).

2.2 Data

The China New Generation Weather Radar (CINRAD) with S band of type A (i.e., CINRAD/SA) is situated in Nanchang (NC) City, which is the capital of Jiangxi Province. The radar station in NC is about 30 km from the southwest shore of PL and about 100 km from the northeast shore of PL (Fig. 1). This range is favorable for detecting the convection information over PL and its shores clearly. In NC City, there is also a sounding station. The radar data and sounding data in NC, and the ground surface temperature data at Duchang are provided by the Meteorological Information Center of Jiangxi Province, China. These observational data may also be obtained from the China Meteorological Information Center. The radar data are the volume scan data in polar coordinate with about 1-km resolution in range and about 1° resolution in azimuth. The improved quality control method of radar echo (Zou et al., 2018) is used to remove the non-meteorological echoes, and then the nearest-neighboring interpolation method (Xiao et al.,2008) is employed to convert the radar data from polar to Cartesian coordinates with a resolution of 0.01° × 0.01°.The ECMWF Reanalysis v5 (ERA5) data are available at https://climate.copernicus.eu/climate-reanalysis, and the NCEP Final (FNL) data used for the WRF boundary and initialization conditions are obtained from https://rda.ucar.edu/datasets/ds083.2/index.html.

Fig. 1. The Poyang Lake (PL) and its surrounding topography (gray shadow) and observational stations. The radar symbol (hollow circle)represents the radar (sounding) station at Nanchang (NC), and the filled circle indicates the observational station of the ground surface temperature at Duchang (DC).

3. Overview of the case on 12–13 August 2015

Some scattered convection occurred around PL from the noon to afternoon on 12 August 2015 (figure omitted), and about 2 h after the sunset (i.e., the sunset time was about 1100 UTC), these scattered convection disappeared. However, by 1818 UTC, some small isolated echoes with the reflectivity more than 20 dBZ appeared at the north shore of PL, and about 12 min later,these isolated echoes rapidly developed into a small isolated convection with the reflectivity more than 40 dBZ(figure omitted). Then, the small isolated convection gradually developed and moved northeastward, and moved out of PL and gradually disappeared at around 1930 UTC (figure omitted).

About half an hour later, some new isolated echoes with the reflectivity more than 20 dBZ reappeared on the northeast shore of PL, and then rapidly developed into a new convection with the reflectivity more than 50 dBZ at 2130 UTC 12 August 2015 (Fig. 2a). Then, this nascent convection gradually developed and moved northeastward, and grew into a northeast–southwest-oriented strong echo belt over the northeast shore of PL at 2200 UTC (Fig. 2b). By 2230 UTC, some new isolated echoes with the reflectivity more than 40 dBZ developed over PL (Fig. 2c). Immediately, the strong echo band over the northeast shore of PL weakened slowly and continued to move northeastward, while echoes over PL strengthened,merged, and formed a long northeast–southwest-oriented strong echo band at 0000 UTC 13 August, which extended from the central PL to the north shore of PL (Fig.2d). Subsequently, the echo band over the northeast shore of PL continuously weakened and then disappeared, while the strong echo band over PL moved northeastward. After 0100 UTC 13 August 2015 (i.e., about 3 h after the sunrise), the strong echo band over PL weakened rapidly and disappeared at about 0130 UTC 13 August 2015 (Fig. 2e), implying the dissipation of this lake-effect convection episode.

The mean composite reflectivity during this lake-effect convection episode is shown in Fig. 2f. It is clear that there is a northeast–southwest-oriented echo band with the reflectivity more than 10 dBZ extending from the central PL to the northeast shore of PL, which is similar to the distribution of strong echoes at 0000 UTC 13 August 2015 (Fig. 2d). However, the maximum region(exceeding 25 dBZ) of the mean composite reflectivity is near the northeast shore of PL rather than over the PL(Fig. 2d), which is directly induced by the long-time maintenance of strong echoes near the northeast shore of PL (Figs. 2a–d). Why do strong echoes on the northeast shore of PL keep a longer time than those over the central PL? The inhomogeneous surface between lake and land may be the main reason, which they may enhance the low-level convergence. It is noted that the echoes to the north of PL (i.e., echoes in the black dotted ellipses in Figs. 2c–f), which occurred in the vicinity of topography with the altitude more than 100 m, may be jointly caused by the lake-effect and topography. Further investigation is needed but beyond the current study.

Fig. 2. Composite reflectivity (dBZ) detected by NC radar at (a) 2130 UTC 12, (b) 2200 UTC 12, (c) 2300 UTC 12, (d) 0000 UTC 13, and (e)0130 UTC 13 August 2015, and (f) mean composite reflectivity from 1800 UTC 12 to 0100 UTC 13 August 2015. The gray line indicates the altitude contour of 100 m.

The weather patterns, which are derived from the ERA5 data, show that before the initiation of the lake-effect convection, a northeast–southwest-oriented low pressure trough at 500 hPa extended from southwest of China to north of Okhotsk Sea, and the main body of the western Pacific subtropical high is located over the South China Sea (Fig. 3a). In this situation, PL was located in front of the low pressure trough and the edge of western Pacific subtropical high, with the relative straight isolines of geopotential height (Fig. 3a). At 925 hPa, PL was to the front of the southwesterly jet, accompanying with strong humidity advection (Fig. 3a). The low-level jet plays an important role in the convection development because it can provide a large-scale moisture supply and convergence (Du and Chen, 2019).

The vertical profiles of pseudo equivalent potential temperature and wind vector over PL (29°N, 116°E)show that before the convection initiation there was a significant convectively unstable layer from 1000 to 800 hPa, while the obvious vertical wind shear was presented under 700 hPa (Fig. 3b). Such vertical structures of pseudo equivalent potential temperature and wind are instrumental in the convection development (Rotunno et al., 1988; Moore et al., 1998). The weather patterns and vertical profiles of pseudo equivalent potential temperature and wind hardly changed during the lake-effect convection episode (figure omitted). Moreover, the sounding data at NC station at 1200 UTC 12 and 0000 UTC 13 August 2015 also exhibit that the convective available potential energy (CAPE) was more than 1500 J kg-1and the lifting condensation level (LCL) was about 970 hPa(Zou, 2020). It is clear that the large-scale circulation background provides a favorable condition for the development of the lake-effect convection over PL.

4. Model setup

4.1 Model configuration

The WRF-ARW (Advanced Research Weather Research and Forecasting), version 4.0, is utilized to simulate the responses of lake-effect convection over PL on the LST variation. The model runs with three one-way nested domains centered at 29.1°N, 116.3°E, including the outer domain with a 15-km horizontal grid spacing,the middle domain with a 5-km horizontal grid spacing,and the inner domain with a 1.67-km horizontal grid spacing on (Fig. 4). The three domains have 161 (141), 121(121), and 100 (91) grids in the east–west (south–north)direction, respectively. There are 33 vertical levels with the model top at 50 hPa.

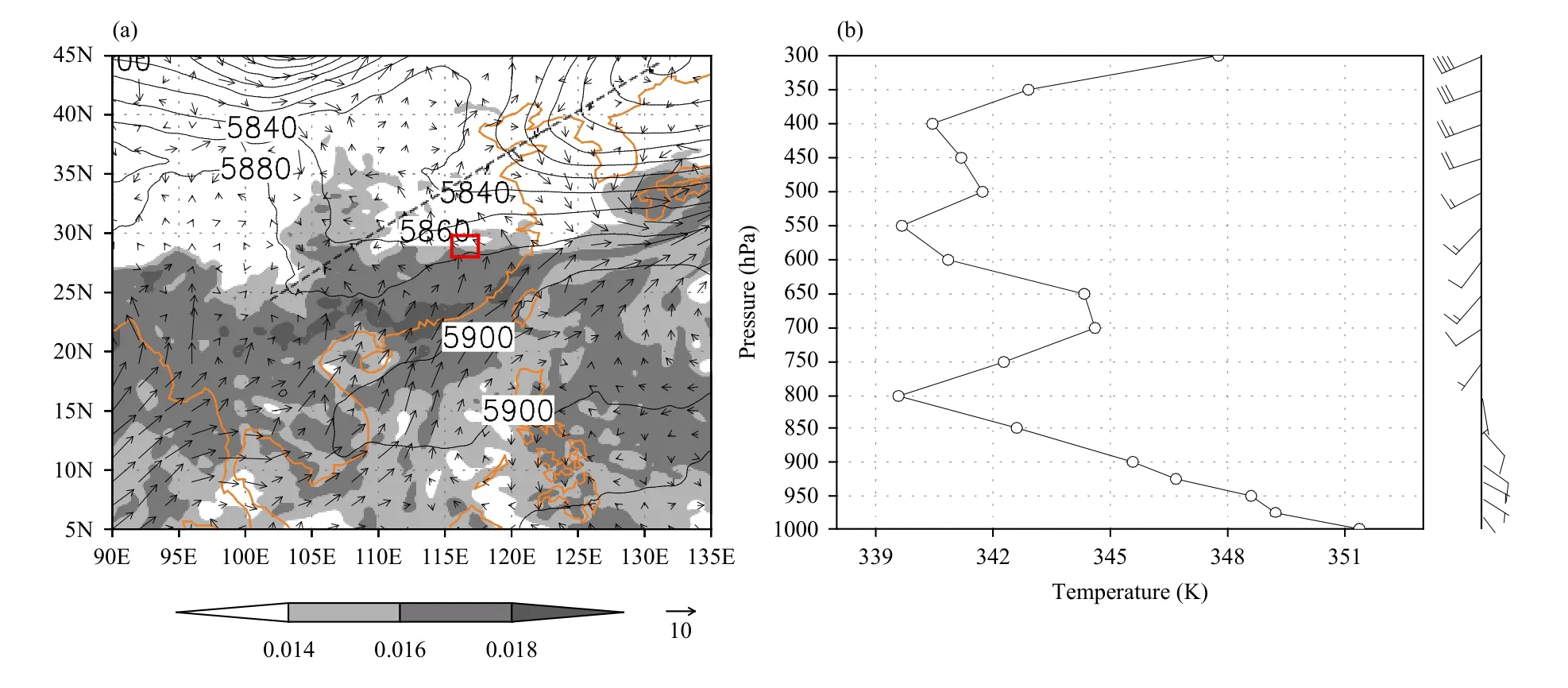
Fig. 3. (a) 500-hPa geopotential (black solid line; gpm), 925-hPa wind vector (m s-1), and specific humidity (shading; kg kg-1) over East Asia;and (b) vertical profiles of pseudo equivalent potential temperature (K) and wind barbs (full and half wind barbs denote 4 and 2 m s -1, respectively) at 29°N, 116°E at 1700 UTC 12 August 2015. The dashed line indicates the 500-hPa trough, the orange line depicts the lake–land boundary line, and the red rectangle represents the PL region in (a).

Fig. 4. The geographic extent of the WRF domains.

Grell–Freitas cumulus parameterization scheme is used in outer domain due to its good performance in southern China (Wu et al., 2018), while no cumulus parameterization schemes are used in the middle and inner domains. Thompson microphysics scheme is used in all the three domains owing to its advantage for simulating lake-effect storm (McMillen and Steenburgh, 2015). Unified Noah model and Yonsei University scheme are employed for the land surface and planetary boundary layer schemes, respectively, as they have been demonstrated successfully in simulating the lake-effect convection over PL (Zou et al., 2021). The scheme of long-wave radiation is set as the Rapid Radiative Transfer Model(RRTM) scheme. Initial and lateral boundary conditions are obtained from the NCEP FNL data, and lateral boundary conditions are updated every 6 hours. Simulation is run for a total of 30 h starting at 0000 UTC 12 August and ending at 0600 UTC 13 August 2015.

4.2 Model setup

Before setting the numerical experiments, the variation characteristics of LST over PL in August should be understood firstly. Xu and Ouyang (1989) analyzed the LST observed by Xingzi hydrological station (in the northern PL) during 1962–1983, and found that the LST was the largest in August with the mean value of 303.05 K and the maximum exceeding 306 K. Recently, Wang et al. (2016) also indicated that the mean LST in August was 302.85 K based on the observation at Xingzi hydrological station during 1960–2015, and pointed out that the LST had obvious diurnal variation in August, with the mean temperature difference of 6 K between the maximum and minimum. Besides, Xu and Ouyang(1989) performed a scientific investigation experiment using ship to measure LST of PL during July–August 1987–1988, and found that the LST had uneven spatial distribution with the highest LST at the north and northeast shores of PL.

In order to investigate the impacts of LST in PL on the lake-effect convection, a control experiment and six sensitivity experiments are conducted. These experiments employ the following surface boundary conditions: 1) in the control experiment (i.e., the CTR), all the lake points within the PL are set to a constant LST of 303 K,which is about the mean LST of PL in August (Wang et al., 2016); 2) six sensitivity experiments include three increase-temperature and three decrease-temperature experiments, and in the three increase-temperature experiments, the LST is set to 304 K (CTR+1K), 305 K(CTR+2K), and 306 K (CTR+3K) across the entire PL.Correspondingly, in the 3 decrease-temperature experiments, the LST is set to 300 K (CTR-3K), 301 K(CTR-2K), and 302 K (CTR-1K) across the entire PL.Here, the experiments with the largest LST (i.e.,CTR+3K) and the smallest LST (i.e., CTR-3K) are designed on the basis of the observed mean temperature difference of 6 K between the maximum and minimum(Wang et al., 2016). The specific descriptions of LST in different experiments are summarized in Table 1.

Table 1. Summary of different experiments

5. Results

5.1 CTR experiment

First, the convection evolution over PL and its surrounding area in the CTR experiment (Fig. 5) is verified against the observation (Fig. 2). At 1830 UTC 12 August 2015, there were isolated echoes with the reflectivity more than 30 dBZ appearing at the north shore and central PL (figure omitted). Then, the echoes at the north shore gradually weakened and disappeared, while the echoes over PL rapidly strengthened and moved northeastward. By 1930 UTC, the echoes had developed into a strong convective storm, with the maximum reflectivity exceeding 50 dBZ (Fig. 5a). Subsequently, the convective storm continued to move northeastward steered by the mid–upper level southwesterly wind (Fig. 6b). At 2030 UTC, the convection moved to the north shore of PL, and formed a strong echo band in a northeast–southwest direction. Meanwhile, some new isolated echoes with the reflectivity more than 30 dBZ or even 40 dBZ appeared over the central PL and east shore of PL (Fig.5b). Immediately, the strong echo band over the north shore of PL gradually weakened and disappeared, whilethe isolated echoes over the central PL and its east shore rapidly strengthened and merged (Fig. 5c). By 2200 UTC, the convective storm developed into a new long northeast–southwest-oriented strong echo band extending to the mid of southwest shore from the northeast shore of PL, with the maximum exceeding 50 dBZ (Fig.5d). This is quite similar to the radar observation at 0000 UTC 13 August, but the location is slightly more southeastward (Fig. 2d). The strong convective storm remained until 2300 UTC 12 August, and then gradually weakened and moved toward the northeast. By 0030 UTC 13 August, the echoes over PL and its shores almost moved out of PL or disappeared, indicating the dissipation of this lake-effect convection episode (Fig. 5e).Compared with the observation, the simulated lake-effect convection by the CTR experiment ends about 1–2 h earlier.

Fig. 5. Composite reflectivity (dBZ) simulated by the CTR experiment at (a) 1930 UTC 12, (b) 2030 UTC 12, (c) 2130 UTC 12, (d) 2200 UTC 12, and (e) 0030 UTC 13 August 2015; and (f) mean composite reflectivity from 1800 UTC 12 to 0100 UTC 13 August 2015.

Figure 5f shows the mean composite reflectivity from 1800 UTC 12 to 0100 UTC 13 August 2015. Although the location is somewhat more southward, the intensity and structure of the simulated echoes are similar to those of the observation (Fig. 2f), with the maximum reflectivity (more than 20 dBZ) in the east shores of PL, reflecting the role of the heterogeneous surface between lake and land. In order to further verify the performance of the CTR experiment, theT–lgpdiagrams of observation and simulation at NC at 1200 UTC 12 August 2015 are shown in Fig. 6. Clearly, the CTR experiment successfully captures the vertical structures of air temperature,humidity (dewpoint temperature), and wind over NC before the lake-effect convection initiation. The small difference of wind at low levels between simulation and observation may be induced by the urban buildings because the sounding station is located in the southwestern part of NC City. On the whole, the CTR experiment has reasonably captured the initiation, development, movement, and intensity of the lake-effect convection over PL occurred on 12–13 August 2015.

It is noted that there are some small differences between the CTR simulation (Fig. 5) and the observation(Fig. 2) in the location and the time evolution of the lakeeffect convection, as well as the strong echo coverage.Why do these differences appear? The LST discrepancy between in the model and the actuality may be the major reason to cause the deviation in the location of lake-effect convection. Specifically, the actual LST in PL has some changes with the time and space, and the areas with a high temperature (about 1-K anomaly) are located at the northern PL (Xu and Ouyang, 1989), which may be induced by the deep water there (Li et al., 2017).However, in the CTR experiment, the LST is set as a constant value, and there is no change with time and space. In addition, the coverage of PL, grid resolution and parameterization schemes of physical processes in the model may also influence the development and evolution of the lake-effect convection. The difference in the dissipation time of the lake-effect convection between observation and simulation will be discussed in the following section.

Fig. 6. The T–lgp diagram of (a) observation and (b) CTR simulation at NC at 1200 UTC 12 August 2015. The temperature (dewpoint temperature) profile is denoted by the red (blue) thick line; the temperature of an air parcel lifted from the surface is denoted by the light blue line; the full and the half wind barbs denote 4 and 2 m s-1, respectively.

5.2 Sensitivity experiment

It can be seen from the simulated composite reflectivity (Fig. 7) that compared with the CTR experiment, the lake-effect convection in sensitivity experiments obviously enhances with the increase of LST, and dramatically weakens with the decrease of LST. In the decreasetemperature experiments (CTR-1/2/3K), at 2200 UTC 12 August 2015, when the lake-effect convection in the CTR was close to mature (Fig. 5d), the intensity and coverage of echoes rapidly decreased with the LST decrease(Figs. 7a–c). When the LST decreased by 1 K, there were only some isolated echoes appearing over PL and its east shore (Fig. 7c). As the LST further decreased by 2 K, almost no echoes occurred over PL, and only some isolated echoes appeared near the east shore (Fig. 7b). Especially, when the LST decreased by 3 K, there were no obvious echoes appearing over PL and its shores (Fig. 7a).It is noted that echoes to the southeast of PL in Fig. 7a may be associated with the topography (Figs. 1, 2).

Compared with the CTR, the lake-effect convection in the increase-temperature experiments (CTR+1/2/3K)evidently enhances, and however, the intensity and coverage of the echoes over PL and its shore do not increase monotonically with the increase of LST (Figs. 7d–f). For example, the area of echoes with the reflectivity more than 55 dBZ in the CTR+1K experiment is equivalent to or even larger than that in the CTR+2K experiment at 2200 UTC 12 August 2015 (Figs. 7d, e). The mean composite reflectivity from 1800 UTC 12 to 0100 UTC 13 August 2015 has also exhibited the similar results, with the maximum reflectivity in the CTR+1K experiment rather than in the CTR+2K or the CTR+3K experiment(Fig. 8). To further confirm the effects of LST on the lake-effect convection, Fig. 9a shows the evolution of the simulated radar reflectivity averaged within the region(28.8°–29.3°N, 116°–116.8°E), where the lake-effect convection mainly occurs in different experiments. As can be seen, in the decrease-temperature experiments the reflectivity increases monotonically with the increase of LST. However, such regularity is not exhibited in the increase-temperature experiments, and the maximum reflectivity occurs in the CTR+1K experiment rather than in the CTR+3K experiment.

Fig. 7. Composite reflectivity (dBZ) simulated by (a) CTR-3K, (b) CTR-2K, (c) CTR-1K, (d) CTR+1K, (e) CTR+2K, and (f) CTR+3K experiments at 2200 UTC 12 August 2015. The solid rectangle represents the region that is used to calculate the mean reflectivity in Fig. 9.

Fig. 8. Mean composite reflectivity (dBZ) obtained from (a) CTR-3K, (b) CTR-2K, (c) CTR-1K, (d) CTR+1K, (e) CTR+2K, and (f) CTR+3K experiments from 1800 UTC 12 to 0100 UTC 13 August 2015.

Fig. 9. (a) Regional mean (28.8°–29.3°N, 116°–116.8°E) composite reflectivity (dBZ) and (b) ground surface temperature at Duchang obtained from the observation and different experiments from 1600 UTC 12 to 0200 UTC 13 August 2015.

The CTR experiment and six sensitivity experiments show that the triggering location and time of lake-effect convection also vary with the LST. For the triggering location, in the CTR-3K, there is no lake-effect convection (Figs. 7a, 8a). In the CTR-2K, the lake-effect convection is triggered at the east shore of PL (Figs. 7b, 8b),and in the CTR-1K, the initiation location moves to PL.When the LST is more than 302 K (i.e., CTR and CTR+1/2/3K), the lake-effect convection is always triggered firstly over PL (Figs. 7, 8). For the triggering time, Fig. 9a exhibits that the higher the LST is, the earlier the echoes over PL and its shore will appear. Specifically, the lake-effect convection is triggered firstly at 2130 UTC 12 August in the CTR-2K, while it is triggered firstly at 2100 UTC in the CTR-1K. In the CTR, the lake-effect convection is initiated at 1830 UTC, while it is triggered at 1800 UTC in the CTR+1/2K. Importantly,in the CTR+3K, the lake-effect convection occurs firstly at 1700 UTC 12 August 2015, which is the experiment with the earliest occurrence of lake-effect convection.

Figure 9a shows that the lake-effect convection in different experiments weakens sharply after 2300 UTC 12 August, and the reflectivity decreases to below 3 dBZ at 0000–0100 UTC 13 August 2015, indicating the dissipation of the lake-effect convection. It is noted that the increase of reflectivity after 0100 UTC 13 August 2015 in different experiments is mainly caused by the echoes crossing PL from the west. However, the observed reflectivity presented a sharp drop after 0100 UTC August 13, and was closed to 0 dBZ at 0200 UTC 13 August 2015, implying the dissipation of the lake-effect convection. This further confirms that the simulated lake-effect convection dissipates 1–2 h earlier than the observation.

Figure 9b displays the ground surface temperature at Duchang during the lake-effect convection episode.Duchang is located on the north shore of PL (Fig. 1) and less affected by the lake-effect convection. Clearly, the simulated and observed ground surface temperature was about 298.5 K at 1600 UTC 12 August 2015, and then the observation was almost with no change while the simulations had small changes with the variation less than 2 K (Fig. 9b). After 2200 UTC August 12, all the simulated ground surface temperature increased rapidly,while the observation rose sharply after 0000 UTC August 12. At 2300 UTC August 12, the ground surface temperature in all experiments was higher than the observation, and at 1 later, it was about 4 K higher than the observation (Fig. 9b). The higher ground surface temperature can reduce the lake–land surface temperature difference and then weaken the lake–land breeze, finally resulting in the weakening and dissipation of the lake-effect convection. It is clear that the earlier dissipation of the lake-effect convection in simulations may be induced by the earlier increase of ground surface temperature around PL.

6. Discussion

6.1 Lake–air exchanges of heat and water vapor

The lake–air interactions, such as the exchanges of heat, water vapor, and momentum between a lake and its overlying air, are the ways that a lake modulates the weather and climate at local to regional scales (Wu et al.,2019). After changing the LST, the changes in effects of a lake on the regional weather and climate are mainly induced by the changes of lake–air heat and water vapor exchanges. Figure 10 shows the distributions of the sensible heat flux in all experiments at 1630 UTC 12 August 2015 (i.e., before the initiation of lake-effect convection).

The sensible heat fluxes over PL gradually enhance with the LST increase. Specifically, in the CTR experiment,the sensible heat fluxes over PL are always positive with the values ranging from 0 to 30 W m-2, indicating a significant upward heat transport (Fig. 10g). In the CTR+1/2/3K (Figs. 10d–f), this upward heat transport over PL obviously enhances, and the strongest transport occurs in the CTR+3K experiment, with the sensible heat flux ranging from 20 to 60 W m-2. However, in the CTR-1/2/3K (Figs. 10a–c), the upward heat transport significant weakens, especially in the CTR-3K experiment, the negative sensible heat fluxes (i.e., the downward heat transport) appear over about half of the PL(Fig. 10a). The simulated latent heat fluxes at 1630 UTC 12 August 2015 also show the similar results. The latent heat fluxes over PL increase with the LST (figure omitted).

In order to examine the variation of sensible and latent heat fluxes in different experiments more clearly, the evolutions of the mean sensible heat and latent fluxes over PL are shown in Fig. 11. Clearly, the sensible heat flux gradually increases with LST, especially before the initiation of lake-effect convection, with the mean increment of about 8 W m-2for the 1-K increase in LST(Fig. 11a). The sensible heat flux in the CTR+3K is almost 10 times larger than that in the CTR-3K, which is related to the larger (smaller) temperature difference between lake and its overlying air in the CTR+3K(CTR-3K) experiment. Moreover, the sensible heat flux in different experiments shows an increasing trend before the sunrise (i.e., 2200 UTC 12 August 2015 in Fig.11a), which may be induced by the decrease in air temperature around the PL due to the radiative cooling of land surface. Similarly, the latent flux also gradually increases with LST, with the mean increment of about 40 W m-2for the 1-K increase in LST, and the latent heat flux in the CTR-3K is only about 30 W m-2, which is about 1/10 of that in the CTR+3K (Fig. 11b).

Since the different sensible and latent heat fluxes among these experiments, the low-level air is also heated and moistened differently. In the CTR-3K (CTR+3K),the low-level air over PL is always cooler (warmer) than that in the CTR during the lake-effect convection episode (Figs. 12a, f). However, in the CTR-1/2K and CTR+1/2K, the low-level air is not always warmer or cooler than that in the CTR. Before the initiation of lakeeffect convection (i.e., 1800 UTC 12 August), the air temperature in the CTR+1/2K (CTR-1/2K) is larger(smaller) than that in the CTR (Figs. 12b–e). When the lake-effect convection develops (especially at the mature and dissipation stages), the low-level air temperature varies complexly, and that in the CTR-1/2K (CTR+1/2K)may be instead warmer (cooler) than that in the CTR(Figs. 12b–e, 9a). This is mainly caused by the convection downdraft and the evaporation cooling of raindrops.Similarly, the low-level air humidity over PL also increases with LST before the initiation of lake-effect convection (Fig. 12). However, after the lake-effect convection forms (especially at the mature and dissipation stages), the specific humidity in mid and lower levels(below 700 hPa) in the CTR-1/2/3K (CTR+1/2/3K) is instead larger (smaller) that that in the CTR (Fig. 12),which may be induced by the strong (weak) transformation of water vapor to hydrometeors associated with the convection (Fig. 9a). Figure 12 also gives that the horizontal wind in mid–low levels over PL is affected less by the LST before the initiation of lake-effect convection,but the large influence appears after the formation of lake-effect convection, which reflects the effect of convection on ambient wind.

Fig. 10. The 10-m wind anomaly (arrow; m s-1) from the CTR experiment and the sensible heat flux (shadow; W m-2) for (a) CTR-3K, (b)CTR-2K, (c) CTR-1K, (d) CTR+1K, (e) CTR+2K, and (f) CTR+3K experiments, and (g) 10-m wind and sensible heat flux at 1630 UTC 12 August 2015. The red rectangle in (g) represents the region that is used to calculate the mean sensible heat and latent fluxes in Fig. 11.

Fig. 11. (a) Averaged sensible heat flux (W m-2) and (b) latent heat flux (W m-2) within the red rectangle in Fig. 10g from 1400 UTC 12 to 0100 UTC 13 August 2015.

6.2 Lake–land breeze

The variation of low-level air temperature caused by the LST variation may induce the variation of near-surface wind. With the increase of sensible heat flux over PL, the 2-m air temperature difference between PL and its adjacent land also increases gradually (Fig. 13a). It is noted that since the irregular shores of PL, for simplicity,the red (black) rectangle in Fig. 10a is regarded as the lake (land) region to draw Fig. 13a. Specifically, in the CTR, the 2-m air temperature difference is about 3.3 K at 1630 UTC 12 August 2015, which is about 1.1 K higher than that in the CTR-3K and 1.3 K lower than that in the CTR+3K (Fig. 13a). As the 2-m air temperature difference between PL and its adjacent land varies, the 10-m wind convergence over PL is also changed. In the CTR,the obvious southerly wind to the south of PL, easterly wind to the east of PL and northeasterly wind to the north of PL converges in the center or north of PL at 1630 UTC 12 August 2015 (Fig. 10g), and the convergence zone is just located at the place where the lake-effect convection initiated after about 2 h. Such wind distribution indicates the lake–land breeze circulation near PL. In the CTR-1/2/3K, the 10-m wind difference between the sensitivity and CTR experiments exhibits an obvious divergence over PL, and the divergence gradually enhances with the decrease of the 2-m air temperature difference (Figs. 10a–c). Conversely, in the CTR+1/2/3K,the 10-m wind difference presents an obvious convergence, and the convergence gradually enhances with the increase of the 2-m air temperature difference (Figs.10d–f). These evidences imply that the lake–land breeze enhances as the 2-m air temperature difference between PL and its adjacent land increases. Regional mean divergence over PL enlarges gradually with the increase of 2-m air temperature difference at 1630 UTC 12 August 2015, which also verifies this viewpoint (Fig. 13b). Note that the mean divergence over PL in the CTR-3K is below 5 × 10-5s-1, which is only about 1/7 of that in the CTR or 1/4 of that in the CTR-2K (Fig. 13b). This is one of the important reasons for the miss of lake-effect convection in the CTR-3K.

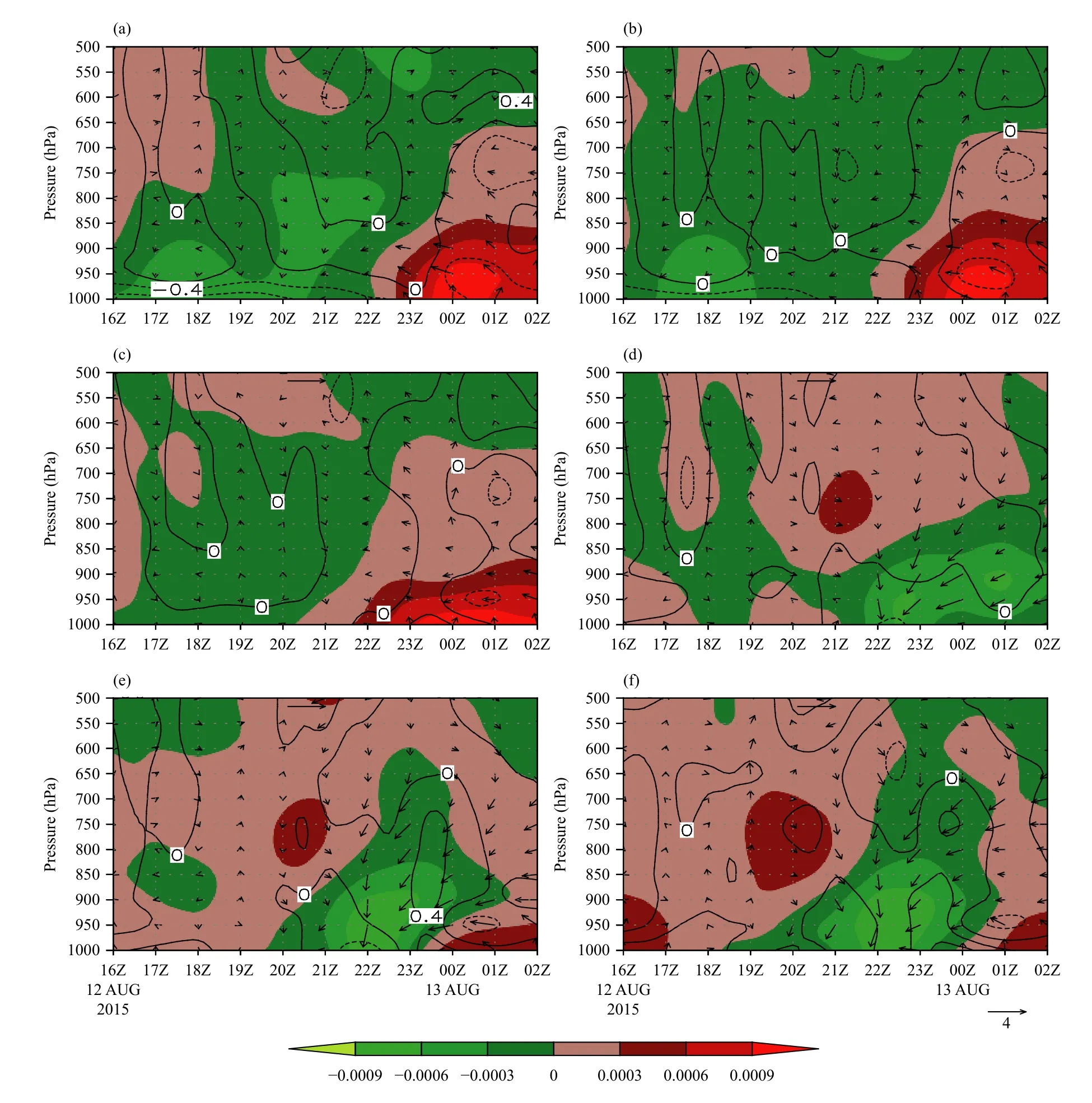
Fig. 12. Time–height section of air temperature anomaly (the solid line represents the positive value and the dashed line represents the negative value; K), air specific humidity (shadow; kg kg-1), and horizontal wind (arrow; m s-1) over PL in the CTR experiment during the lake-effect convection for the (a) CTR-3K, (b) CTR-2K, (c) CTR-1K, (d) CTR+1K, (e) CTR+2K, and (f) CTR+3K experiments.

6.3 CAPE

The changes of low-level air temperature and humidity associated with the LST variation may result in the change of atmospheric stability. CAPE is an important index to evaluate whether the atmosphere is stable or whether the convection is easy to develop, and has been widely used to analyze the potential of convective storm or precipitation (Fujinami et al., 2020; Zhao et al., 2020;Zou et al., 2020). Figure 14 displays the evolution of the mean CAPE over PL (i.e., the red rectangle region in Fig.10g) in all experiments from 1400 UTC 12 to 0100 UTC 13 August 2015. It is clear that before the initiation of lake-effect convection, the CAPE over PL enlarges gradually with LST due to the enhancement of heating and moistening of PL on its overlying air (Fig. 11). Excepting for the CTR-1K and CTR-2K experiments, all experiments have produced the CAPE more than 2000 J kg-1before the initiation of lake-effect convection,providing a favorable unstable condition for the convection development. As also can be seen from Fig. 14, the CAPE in different experiments (especially in the CTR and CTR+1/2/3K) exhibits an increasing trend with time before the initiation lake-effect convection, indicating the accumulation of energy available. After the initiation of lake-effect convection, the CAPE over PL gradually decreases, implying the release of energy.

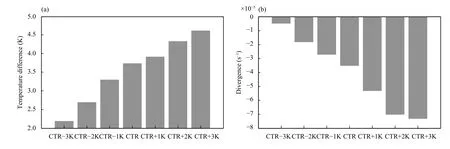
Fig. 13. (a) The 2-m air temperature difference between PL and its adjacent land, and (b) mean divergence of 10-m wind over PL (i.e., the red rectangle in Fig. 8a) at 1630 UTC 12 August 2015 in different experiments.

Fig. 14. Averaged CAPE over PL from 1400 UTC 12 to 0100 UTC 13 August 2015.

6.4 Level of free convection

The above analysis shows that the lake–land breeze near PL and the CAPE over PL enhance gradually with the increase of LST. The strong lake–land breeze can produce the convergence of low-level air and provide the lifting condition for convection initiation, while the large CAPE can provide the energy for the convection development. Therefore, this can explain that the lake-effect convection occurs earlier with the increase of LST, and that the strong (weak or even no) lake-effect convection appears in the increase-temperature (decrease-temperature) experiments because of the strong (weak) lake–land breeze and the large (small) CAPE (Figs. 13b, 14).

Nevertheless, the lake-effect convection over PL is not strictly enhanced with LST. In the CTR+2/3K, the intensity of lake-effect convection is slightly weaker than that in the CTR+1K (Fig. 9a). Why does this situation appear? In fact, the calculation formula of CAPE (Li et al., 2010) can be expressed as follows:

whereTvis the virtual temperature of the uplifting air parcel,Tveis the virtual temperature of the ambient air,zfis the level of free convection (LFC), andzeis the equilibrium level. Clearly, the CAPE indicates the energy that ambient air does work on an air parcel, which may be converted into the kinetic energy of upward motion.However, the release of CAPE requires that the air parcel needs to be uplifted to above the LFC. Therefore,how much the CAPE can be released is closely related to the intensity of uplifting motion in low level and the height of LFC. Although Figs. 10 and 13b show that the low-level uplifting motion (i.e., convergence) gradually strengthens with the increase of LST, the LFC does not monotonically increase or decrease with the LST before the initiation of lake-effect convection, and the minimum occurs in the CTR+1K (Fig. 15). This may be the main reason that the strongest lake-effect convection occurs in the CTR+1K instead of the CTR+3K.

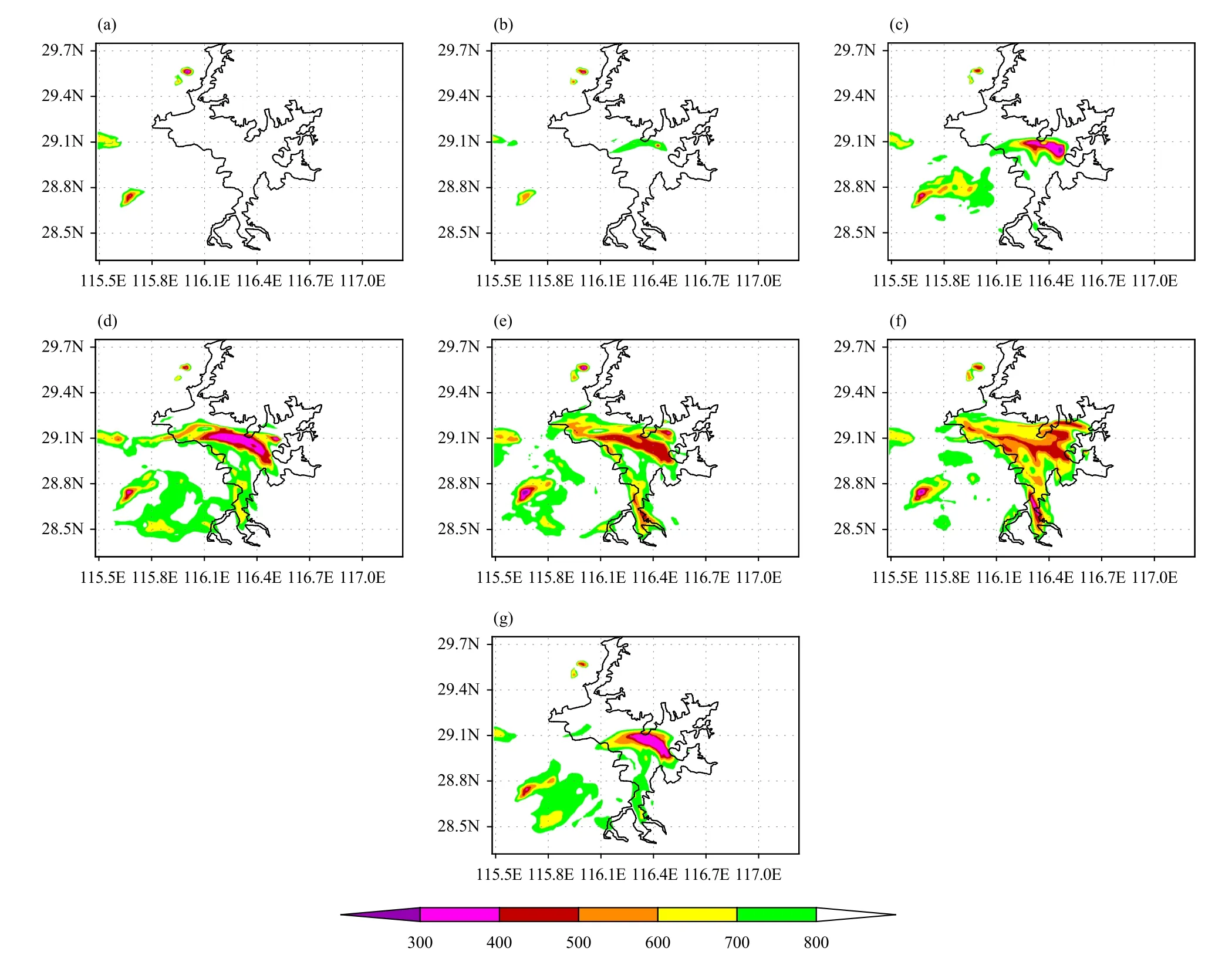
Fig. 15. Level of free convection (shadow; m) obtained from the (a) CTR-3K, (b) CTR-2K, (c) CTR-1K, (d) CTR+1K, (e) CTR+2K, (f)CTR+3K, and (g) CTR experiments at 1630 UTC 12 August 2015.

Why does not the LFC increase or decrease monotonically with the increase of LST? The LFC is the altitude in the atmosphere where the saturated air parcel becomes warmer than the surrounding air and begins to rise freely. Actually, it is the height of the first intersection between the moist adiabatic line started from lifting condensation level (LCL) and the stratification curve of ambient temperature. Clearly, it is complex to determine the LFC because it is jointly influenced by the LCL, the temperature of air lifted to LCL from near surface and the ambient temperature. Since the effect of LST on the air temperature above the boundary layer is relatively small before the initiation of lake-effect convection, the influence of LST on the LFC mainly depends on the LCL and temperature of air lifted to the LCL from near surface(i.e., the location of LCL in the temperature–height section). However, the LCL and temperature of air lifted to the LCL from near surface are also mainly determined by the air humidity and temperature at near surface. The LCL can be approximately expressed as follows(Schrieber et al., 1996):

whereZlis the height of LCL,a= 125 m K-1is a constant,Tis the temperature of air parcel at near surface,andTdis the dewpoint temperature, which indicates the moisture content of atmosphere. Thus, the temperature of air lifted to LCL from near surface (TLCL) can also be expressed as follows:

where γd= 9.8 K km-1is the dry-adiabatic lapse rate.

Although the temperature and dewpoint temperature of near-surface air over PL increase monotonically with LST, their difference (T-Td) may not vary monotonically with LST, finally resulting in the non-monotonous variations ofZlandTLCL. In fact,Tdis the temperature when the air is cooled to saturation under the condition of constant water vapor content and pressure, and it has a nonlinear (logarithmical) relationship with the water vapor content (Zhang and Xi, 2011). Therefore, even if the water vapor content and air temperature increase monotonically with LST,TdandT-Tdmay not vary monotonically, andTLCLmay not also vary monotonically with LST based on Eq. (3). The variableTLCLin different experiments at 1630 UTC 12 August 2015 also confirms this point (Fig. 16). Note that there are different spatial distributions of LFC among the experiments (Fig. 15),andTLCLhas similar spatial distributions (Fig. 16). This suggests thatTLCLis an important factor to influence LFC,and the spatial variation ofTLCLis associated with the distribution of near-surface air temperature and humidity.

Fig. 16. Temperature (K) of air lifted from near surface to the LCL by the dry-adiabatic lapse rate for the (a) CTR-3K, (b) CTR-2K, (c)CTR-1K, (d) CTR+1K, (e) CTR+2K, (f) CTR+3K, and (g) CTR experiments at 1630 UTC 12 August 2015.

7. Conclusions

In this study, we have investigated the effects of LST on the lake-effect convection over PL, which occurred on 12–13 August 2015, by applying a high-resolution WRF model. A CTR experiment and six sensitivity experiments were conducted to quantify to what extent the LST of PL can influence the lake-effect convection. In the CTR, the LST was set to the mean temperature of 303 K in July or August. Six sensitivity experiments include three increase-temperature (CTR+1/2/3K) experiments and three decrease-temperature (CTR-3/2/1K) experiments. In the CTR-3/2/1K, the LST was set to 300, 301,and 302 K, respectively, while it was set to 304, 305, and 306 K, respectively, in the CTR+1/2/3K.

The simulation results show that the CTR has reasonably reproduced the lake-effect convection, successfully capturing the initiation, development, movement, and intensity of the lake-effect convection over PL. The lakeeffect convection in sensitivity experiments is markedly affected by the LST of PL. The initiation time, initiation location, and intensity of lake-effect convection varies with the variation of LST. With the increase of LST, the initiation time of the lake-effect convection advances gradually, and in the CTR+3K, it is triggered at 1700 UTC 13 August 2015, which is the earliest among all experiments. When the LST is more than 301 K, the initiation location of the lake-effect convection moves to over PL from its shore. Moreover, in the CTR+1/2/3K(CTR-3/2/1K), the lake-effect convection strengthens(weakens) remarkably compared with that in the CTR. In particular, no lake-effect convection occurs in the CTR-3K. However, interestingly, the lake-effect convection does not strictly monotonically intensify with LST,and the strongest one occurs in the CTR+1K rather than in the CTR+3K.

Corresponding diagnostic analysis shows that with the increase of LST, the upward sensible heat and latent heat fluxes are enhanced gradually, which can strengthen the lake–land breeze circulation and enlarge the CAPE over PL. This could explain why the initiation time and location of the lake-effect convection vary with LST, and why the strong (weak) lake-effect convection occurs in increase-temperature (decrease-temperature) experiments. In addition, although the temperature and dewpoint of near-surface air increase monotonically with LST, their difference does not vary monotonically with LST. This leads to that the LCL and the temperature of air lifted to LCL from near surface do not vary monotonically with LST, resulting in the non-monotonic variation of LFC with LST and the lowest LFC in the CTR+1K rather than in the CTR+3K. It is responsible for the strongest convection occurring in the CTR+1K instead of the CTR+3K.

This study has exhibited that the LST is an important factor that affects the lake-effect convection over PL.However, in fact the LST in PL has certain spatiotemporal variations, and the effects of its spatiotemporal variation on lake-effect convection should be further studied.Meanwhile, in order to improve the numerical forecast skill of lake-effect convection over PL, it is required to get an accurate and dynamic estimation of LST in regional numerical weather forecast model. Recently, a one-dimensional mass and energy balance lake model from the Community Land Model to dynamically simulate the lake–air interaction has been coupled into the WRF model,and verified and used in many lakes in China, such as the Taihu Lake (Gu et al., 2016), Ngoring Lake (Wen et al.,2015), and Lake Nam Co (Dai et al., 2018; Wu et al.,2020). Therefore, the lake model should be verified and used in PL to improve the simulations of lake–air interaction and lake-effect convection in the future work. Besides, other factors, such as the hills around PL, the large-scale flow patterns, and the NC urban area located to the southwest of PL, also should be considered to get a more comprehensive understanding of the lake-effect convection over PL.

Acknowledgments.We thank two anonymous reviewers for insightful comments that guided the revision of the manuscript, and Nanjing Hurricane Translation for reviewing the English language quality of this paper.