例谈解析几何中的特殊、对称与极限思想的应用
广东省中山市中山纪念中学(528454) 李文东
解析几何中的离心率和定点与定值问题,是高考重点考查的内容之一,综合性较强.试题充分考查方程思想,函数思想,转化与化归等数学思想的熟练运用能力,有利于促进学生逻辑推理,数学运算,直观想象等数学核心素养的提升,同时圆锥曲线又具有很好的对称性,在上述一些问题的求解中,如果我们能充分利用圆锥曲线的对称性,并且借助特殊和极限的思想去思考,往往能够对问题起到简化作用.
一、利用对称性巧求离心率
圆锥曲线具有良好的对称性,在一些有关离心率问题的求解中,我们要善于利用这种对称性,达到简化计算的目的.
例1过双曲线的右顶点A作斜率为-1 的直线l,直线l与双曲线的两条渐近线的交点分别为B,C, 若则双曲线的离心率为____.
解如图1, 由双曲线的对称性, 作C关于y轴的对称点D,该点位于渐近线y=上.因为所以于是|CD|=2a,点C的坐标为(-a,b),又因为kAC=-1,∠OAC= 45°.在等腰直角三角形ΔAMC有b=2a,从而求得离心率为
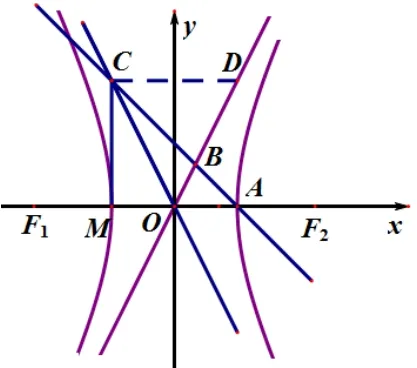
图1
点评本题常规的做法是写出直线l的方程,然后与双曲线方程联立解方程组求出点B,C的坐标,代入--→BC= 2-→AB求解,运算量较大.
例2已知F1,F2为双曲线的左、右焦点,过点F2作此双曲线一条渐近线的垂线,垂足为M,且满足则此双曲线的离心率是( )
解由题意F2(c,0),双曲线的渐近线方程为bx±ay=0,则F2到渐近线的距离而|OF2|=c,故|OM|=a.于是根据双曲线的对称性, 过双曲线的左焦点F1作渐近线的垂线, 垂足为N, 则如图2, 在RtΔMNF1中,MN2+NF21=MF21, 即4a2+b2= 9b2,从而
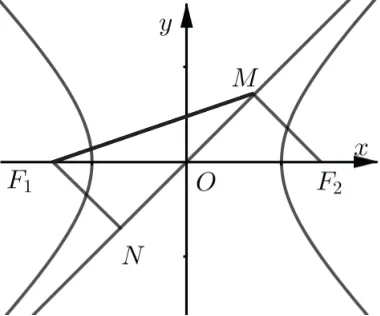
图2
点评本题运用双曲线的对称性,巧妙的将MF2转化为NF1,从而将MF2与MF1转化到RtΔMNF1中,达到顺利求解.
二、特殊、对称与极限思想在定点定值问题中的应用
定点定值问题反映的是圆锥曲线变化中的不变性,此类问题对计算能力要求较高,对于这类问题我们要善于利用特殊、对称与极限思想去判断定点或定值的特征,明确计算的方向.
例3设P(x0,y0)为椭圆上一点,过点P作斜率互为相反数的两条直线PA、PB,分别交椭圆于A、B两点,则直线AB的斜率为定值____.
分析作为一道填空题,我们可以运用极限思维得到结果: 设点P(x0,y0)关于x轴的对称为P′(x0,-y0),由于直线PA、PB的斜率互为相反数,则直线PA、PB关于直线PP′对称,利用极限的思想,当点A无限接近点P′时,点B也无限接近点P′,此时直线AB即为椭圆在点P′处的切线,从而直线AB的斜率为椭圆在点P′处的切线的斜率,由于椭圆在点P′处切线的斜率为故直线AB的斜率为具体证明略.
点评关于椭圆的内接四边形ABCD有如下结论: 若kAB+kCD= 0,kAD+kBC= 0,kAC+kBD= 0, 若其中一个成立, 则另外两个也成立.运用极限思想: 设想当点A,D无限接近时, 此时四边形ABCD变为三角形ABC,kAB+kCD= 0,kAD变为椭圆在点A处切线的斜率,且该斜率等于BC的斜率(为定值)!
例4过椭圆上一点P(x0,y0)作两条相互垂直的弦PA,PB,证明: 直线AB过定点.
分析本例仅运用极限与特殊思维来找定点, 不对一般性作证明.当点A无限接近点P时, 弦PA为椭圆在点P(x0,y0)处的切线,其方程为由于PA⊥PB, 故直线PB的方程为b2x0(y-y0)=a2y0(x-x0),此时它也是直线AB的方程.
又取点P(x0,y0)分别关于x轴和y轴的对称点A(x0,-y0),B(-x0,y0), 显然点A,B均在椭圆上,且PA⊥PB, 而此时直线AB的方程为y0(x+x0)+x0(y-y0)=0.由
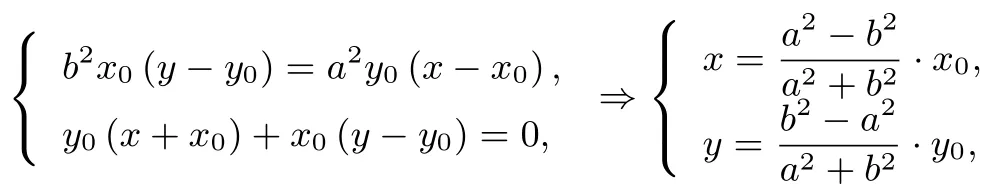
从而直线AB过定点
例5(2020年高考全国I卷理科第20 题)已知A,B分别为椭圆的左、右顶点,G为E的上顶点,如图3,P为直线x= 6 上的动点,PA与E的另一交点为C,PB与E的另一交点为D.
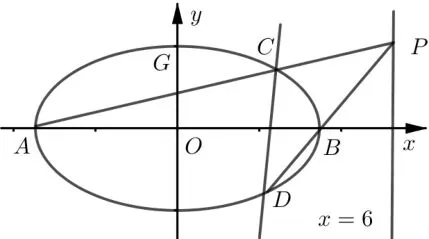
图3
(1)求E的方程;
(2)证明: 直线CD过定点.
分析我们分析CD过定点的特点: 先利用特殊思想,当点P为直线x=6 与x轴的交点P(6,0)时,此时PA与E的另一交点C即为点B,PB与E的另一交点D即为点A,直线CD即为x轴,因此定点必在x轴上.也可以利用对称的思想,设P为x轴上方的点,点P关于x轴的对称点为P′,由对称性不难知道,直线P′A与E的另一交点C′与点C关于x轴对称,P′B与E的另一交点为D′与点D关于x轴对称,从而直线CD与直线C′D′关于x轴对称,因此其交点必在x轴上,即直线CD过x轴上的定点.由以上分析,设P(6,y0),我们只需要得到直线CD的方程,然后令y=0,证明其横坐标为定值即可.
解(1)椭圆方程为:
(2)设P(6,y0),则直线AP的方程为:联立直线AP的方程与椭圆方程可得:整理得:(y20+9)x2+ 6y20x+ 9y20-81 = 0, 解得:x=-3 或将代入直线可得:所以点C的坐标为同理可得: 点D的坐标为所以直线CD的方程为:y - yD=代入坐标并整理可得:
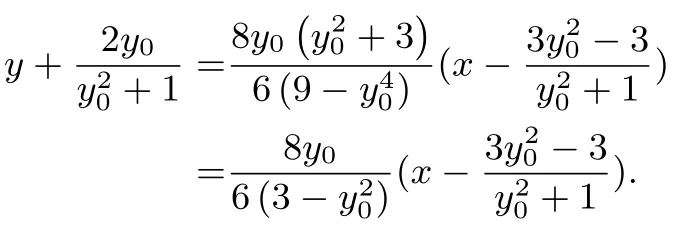
令y= 0 得故直线CD过定点
例6已知椭圆的离心率为点在椭圆C上.
(I)求椭圆C的方程;
(Ⅱ)在x轴上是否存在一定点E,使得对椭圆C的任意一条过E的弦为定值? 若存在,求出定点和定值;若不存在,请说明理由.
分析本题第2 问是一个关于定点定值的探究性问题,由于定点E和定值均未知,计算无从下手,利用特殊思想探路,设E(x0,0),分别过E取两垂直于坐标轴的两条特殊弦CD,C′D′,由此可以确定定点和定值,然后对一般性进行证明即可.
解(I)椭圆C的方程为
(Ⅱ)设E(x0,0), 分别过E取两垂直于坐标轴的两条弦CD,C′D′, 则即解得x0=所以若存在必为定值为6.下证满足题意.设过点的直线方程为代入C中得:设A(x1,y1),B(x2,y2),则