关于圆锥曲线焦半径长的倒数和

重庆市铜梁二中(402560) 李波

在[1]中,作者利用诱导公式给出了圆锥曲线焦半径倒数和为定值的部分结论.受此文启发,本文将[1]中的结论推广到一般情形,并得到圆锥曲线焦半径倒数和的统一表达式.最后,探究了焦半径倒数和的一个变式,得到了几个较弱的结论.

一、一个统一的结论

性质1设F是椭圆的左焦点,过F的焦半径FP1,FP2,··· ,FPn(n≥2)满足条件:任意相邻两条焦半径的夹角为

证明以F为极点,射线FO为极轴,建立极坐标系,则椭圆C的极坐标方程为:e为离心率.若P1的极角为α, 则P2,P3,··· ,Pn的极角分别为于是,进而

熟知下面两个事实:

(i)xn= 1 的全部复根(即n次单位根)为ωj=其中i为虚数单位;

(ii)复数eθi的n次方根为

双曲线上也有类似的结论,即:

性质2设F是双曲线的右焦点,过F的焦半径FP1,FP2,··· ,FPn(n≥2)满足条件: 任意两条相邻焦半径的夹角为

类似于性质1 的证明,还可以得到

性质3设F是抛物线C:y2=2px(p ＞0)焦点,过F的焦半径FP1,FP2,··· ,FPn(n≥2)满足条件: 任意两条相邻焦半径的夹角为

注记对于性质1 中的椭圆和性质2 中的双曲线,焦点到相应准线的距离是记,则而性质3 中的抛物线的焦准距就是标准方程中的p且抛物线的离心率为1,则ep=p.如果把圆锥曲线的焦准距统一用p表示,那么前面的三条性质可统一写成:

结论设F是圆锥曲线Γ 的焦点,F到相应准线的距离为p, 过F的焦半径FP1,FP2,··· ,FPn(n≥2)满足条件: 任意两条相邻焦半径的夹角为(e是Γ 的离心率).

二、一类变式探究

对圆锥曲线焦半径倒数和作一个变式,也可以得到一类较弱的结论.下面只给出抛物线和椭圆上的相关结论,双曲线上的类似结论不再详述.

性质4设F是抛物线C:y2= 2px(p ＞0)焦点, 过F的焦半径FP1,FP2,··· ,FPn(n≥2)分别与圆交于M1,M2,··· ,Mn且任意两条相邻焦半径的夹角为,则

(1)当n=2 时,

(2)当n=4 时,

证明在以F为极点,F向x轴正方向作的射线为极轴的极坐标系下,C和圆F的方程分别为设P1(ρ,θ), 则即

(1)当n=2 时,

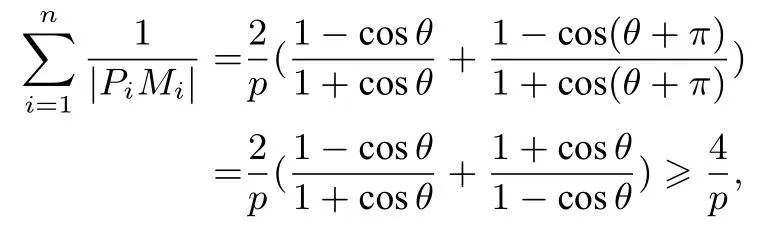
(2)当n=4 时,

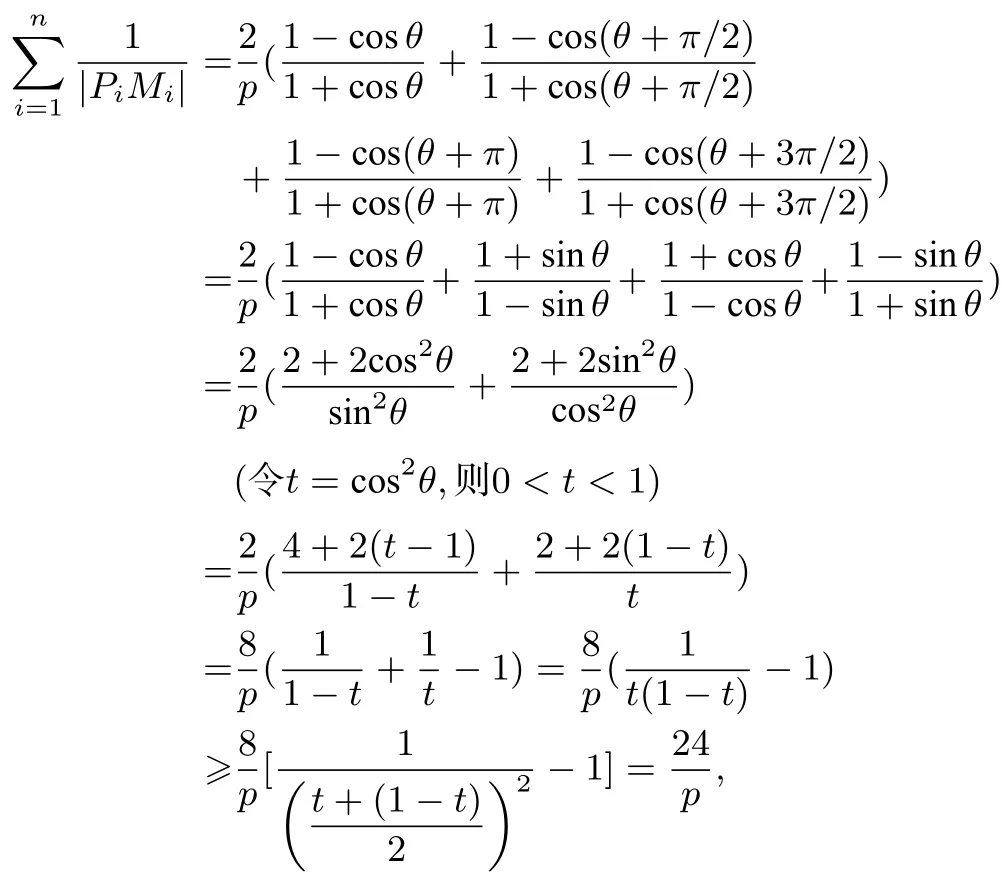
性质5设F(c,0)是椭圆的右焦点, 焦半径FP1,FP2,··· ,FPn(n≥2)分别与圆F: (x-c)2+y2= (a-c)2交于M1,M2,··· ,Mn且任意两条相邻焦半径的夹角为e为C的离心率,则

(1)当n=2 时,

(2)当n=4 时,

证明设椭圆C的右顶点为A,在F为极点,射线FA为极轴的极坐标系下,C的方程为(p为焦准距).令P1(ρ,θ),则即

(1)当n=2 时,

(2)当n=4 时,

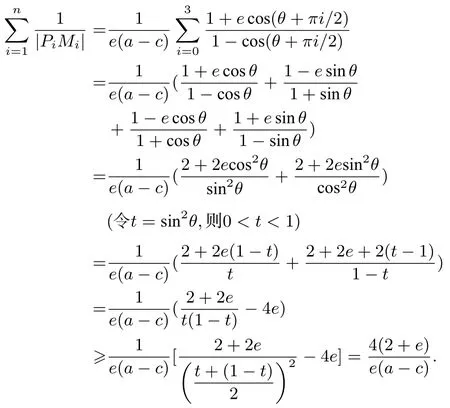
类似于性质5 的证明,可得

性质6设F(-c,0)是椭圆的左焦点, 焦半径FP1,FP2,··· ,FPn(n≥2)分别与圆F: (x+c)2+y2= (a+c)2交于M1,M2,··· ,Mn且任意两条相邻焦半径的夹角为e为C的离心率,则

(1)当n=2 时,

(2)当n=4 时,

最后,提供一个练习题目.

练习(2020 武汉6月模拟)已知过抛物线C:y2= 4x的焦点E的直线交C于P,Q两点,交圆x2+y2-2x= 0于M,N两点,其中P,M位于第一象限,则的最小值为____.(答案: 2.)