基于GeoGeb ra软件圆柱形螺旋线的可视化

胡桐庆 刘 丹 谢恩东

（安庆市第一中学 安徽 安庆 246003）

数学中螺旋线的种类较多，在物理学中出现较多的是圆柱形螺旋线，物体做匀速圆周运动与沿轴线匀速直线运动的合运动轨迹就是等距螺旋线，生活中弹簧是较常见的等距螺旋线，利用GeoGeb ra软件可以很好地演示圆柱形等距螺旋线［1］.

1 等距螺旋线的得到

由于等距螺旋线是三维曲线，可在GeoGeb ra的3D视图中完成，等距螺旋线很难用单一的方程来表示，但可以结合其参数方程和“曲线”指令来绘制.在指令栏输入：曲线（2t，3cos（2πt），3sin（2πt），t，0，6），得到曲线a就是等距螺旋线，如图1所示，从指令中不难发现曲线a是以速度2 m·s-1沿x轴匀速运动与垂直x轴半径为3 m、周期为1 s的匀速圆周运动的合运动在时间0～6 s内的轨迹.

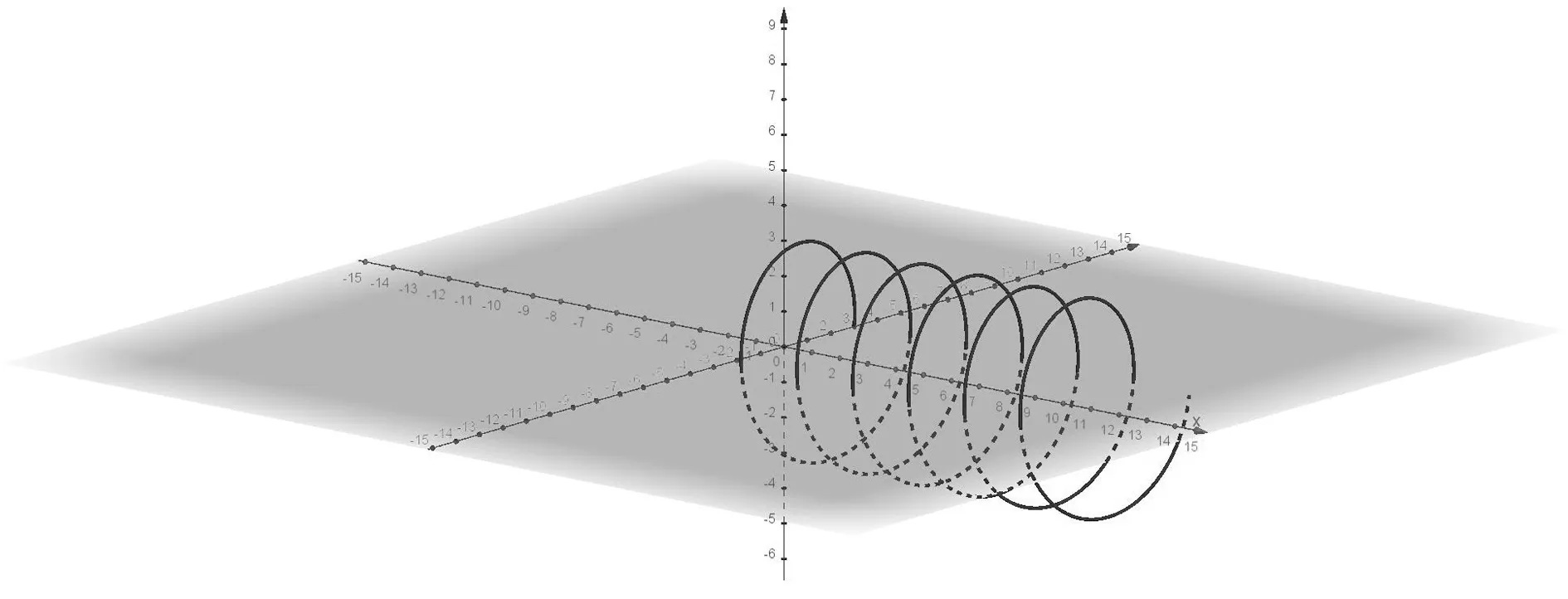
图1 等距螺旋线

2 弹簧类问题

弹簧的形状就是等距螺旋线，弹簧在物理学中很常见.

（1）弹簧振子

弹簧振子的运动是最简单的简谐运动，弹簧振子构造也很简单，由轻弹簧和小球组成.

①描点A，其位置设置为：（5+2sin（t），0，0），其中t为时间，用滑动条表示，A的运动为简谐运动，以A为球心绘出小球表示振子.

②指令栏输入：曲线（x（A）／20k，0.1cos（2πk），0.1sin（2πk），k，0，20），得到的弹簧一端随A点位置变化而变化.

③指令栏输入：向量（（5，0，0.3），（x（A），0，0.3）），得到向量u可表示位移x的动态变化，指令栏输入：向量（（x（A），0，0.5），（x（A），0，0.5）-0.6u），得到向量v可表示加速度a的动态变化，效果如图2所示，启动滑动条t的动画功能就可看到弹簧振子振动的动态过程.

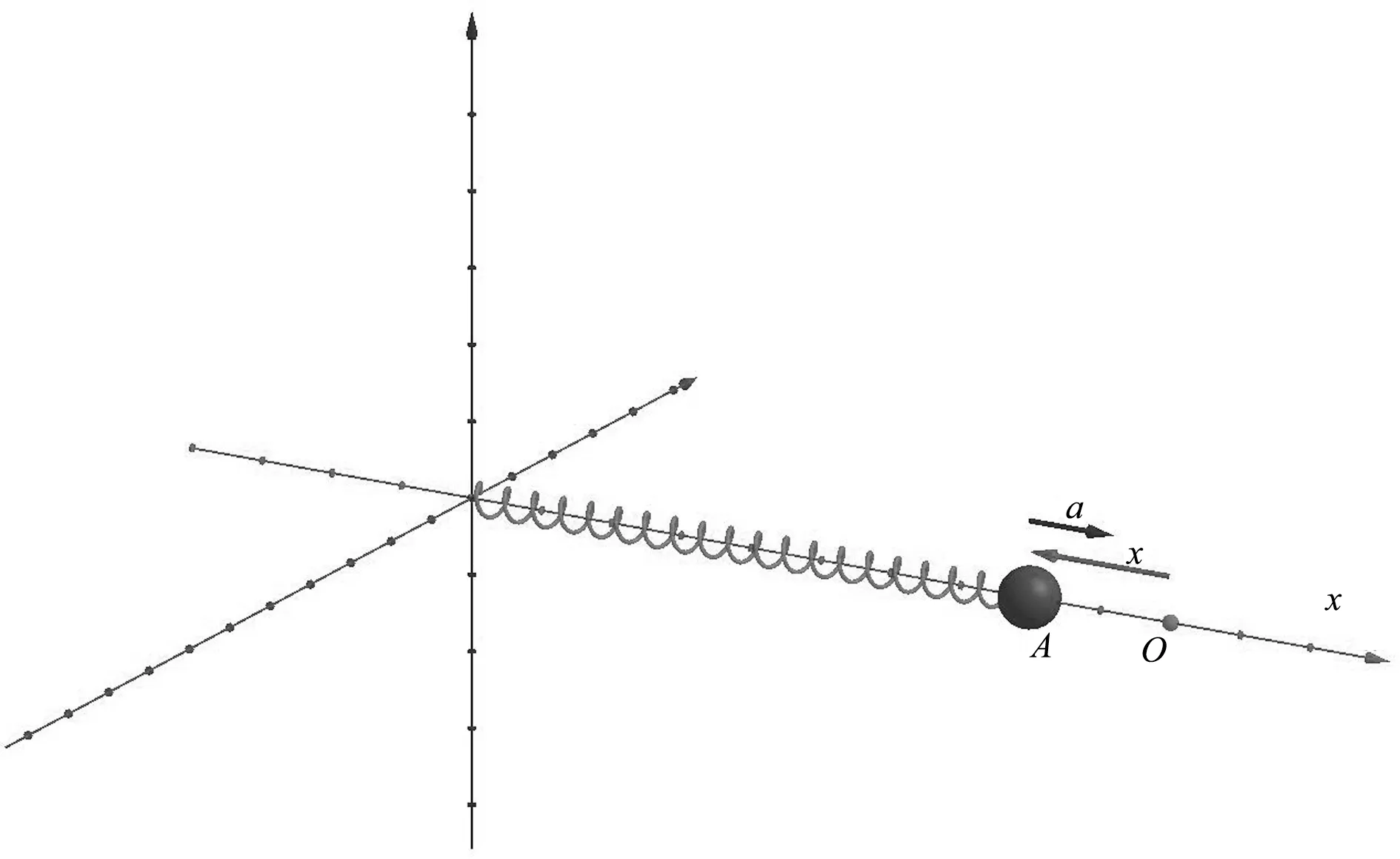
图2 弹簧振子

（2）物体沿光滑弹簧下滑

【例1】如图3所示，一根长度为L的光滑钢丝绕成一高度为H的弹簧（不计形变），此弹簧竖直放置.有一中间有孔的小球由构成弹簧的钢丝穿过并从弹簧的最高点A释放，小球沿弹簧下滑，求经过多长时间小球到达弹簧的最低点B.

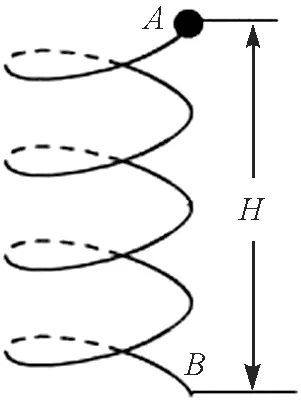
图3 例1题图

解析：弹簧可以认为分布在圆柱面上，小球沿光滑弹簧下滑时机械能守恒，可以假想在不改变弹簧上各处倾角的条件下将弹簧拉直成一条直线，小球沿此直线下滑的时间与题中要求的时间相等.

小球沿直线下滑的加速度

由几何知识可得

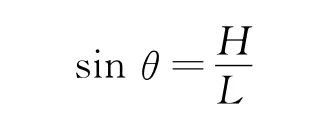
由位移公式可知

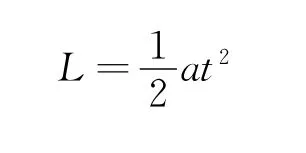
解得

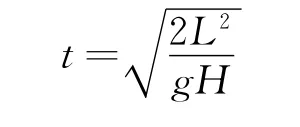
制作方法如下.

（1）指令栏输入：曲线（2cos（0.5k︿2），2sin（0.5k︿2），8-0.125k︿2，k，0，8），得到曲线表示题中光滑弹簧.

（2）指令栏输入：（2cos（0.5t︿2），2sin（0.5t︿2），8-0.125t︿2），得到点C可以表示物体位置，如图4所示，启动滑动条t的动画功能就可看到物体的下滑过程，显示C点轨迹还能得到运动的频闪图，如图5所示，物体的位置能反映物体的加速过程.

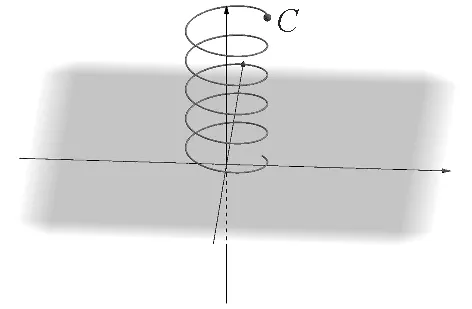
图4 物体沿光滑弹簧下滑

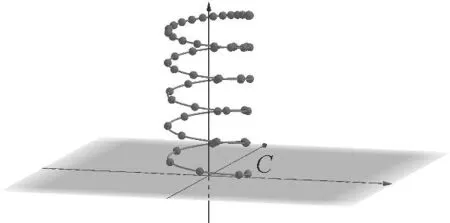
图5 物体下滑频闪图

3 带电粒子在匀强磁场中的运动轨迹

当带电粒子的速度方向与磁感线成一定夹角时，可将粒子速度沿磁场方向和垂直磁场方向正交分解，粒子的运动可分解为沿磁场方向的匀速直线运动和垂直磁场平面内的匀速圆周运动，其轨迹是一条等距螺旋线.

【例2】从电子枪打出的电子流并不完全沿直线运动，而是有微小角度的散射，为了使显示器图像清晰，需要通过电子透镜对电子流进行聚焦处理，正好在屏幕上汇聚形成一个亮点.如图6（a）所示，密绕线圈的玻璃管是一种利用磁场进行汇聚的电子透镜，又称为磁场透镜.如图6（b）所示为其内部原理图，玻璃管的管长为L，管内直径为D，管内存在沿轴线方向向右的匀强磁场.电子流中的电子在与轴线成微小角度θ的顶角范围内从轴线左端的O点射入磁场，电子速率均为v0，调节磁感应强度B的大小，可以使电子重新汇聚到轴线右端与荧光屏的交点P.已知电子的电荷量为e，质量为m，当角度θ非常小时满足cosθ=1，sinθ=θ，若要使电子流中的电子均能汇聚到P点，下列说法正确的是（ ）

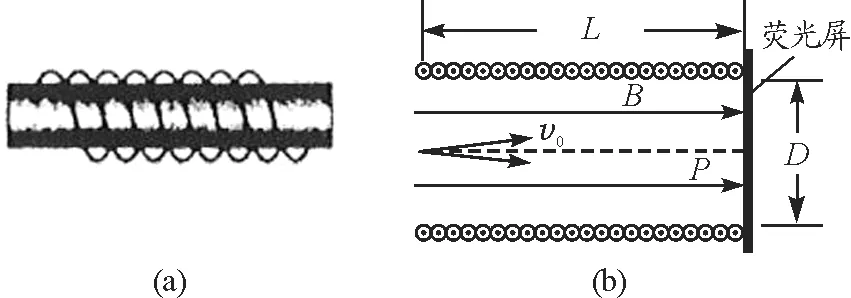
图6 例2题图

A.磁感应强度应满足B=（n为合适的整数）

B.磁感应强度应满足B=（n为合适的整数）

答案：A，C.

解析：电子的轨迹为螺旋线，沿磁场方向做匀速直线运动，垂直磁场方向做匀速圆周运动，周期为，两分运动时间相等即

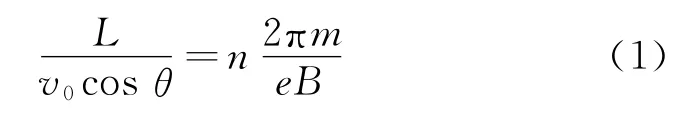
其中n为环绕周数，如图7～9所示，又题中

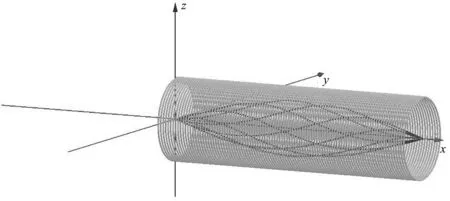
图7 粒子轨迹（n=1）

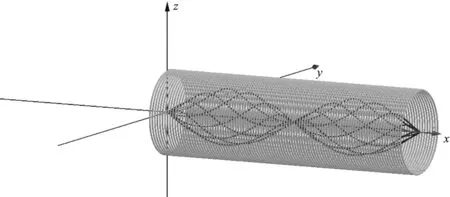
图8 粒子轨迹（n=2）

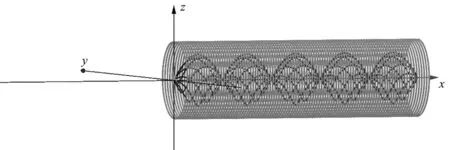
图9 粒子轨迹（n=5）

结合式（1）、（2）可得

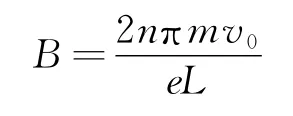
匀速圆周运动半径

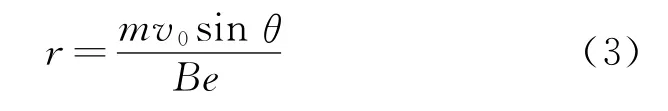
由图10可知

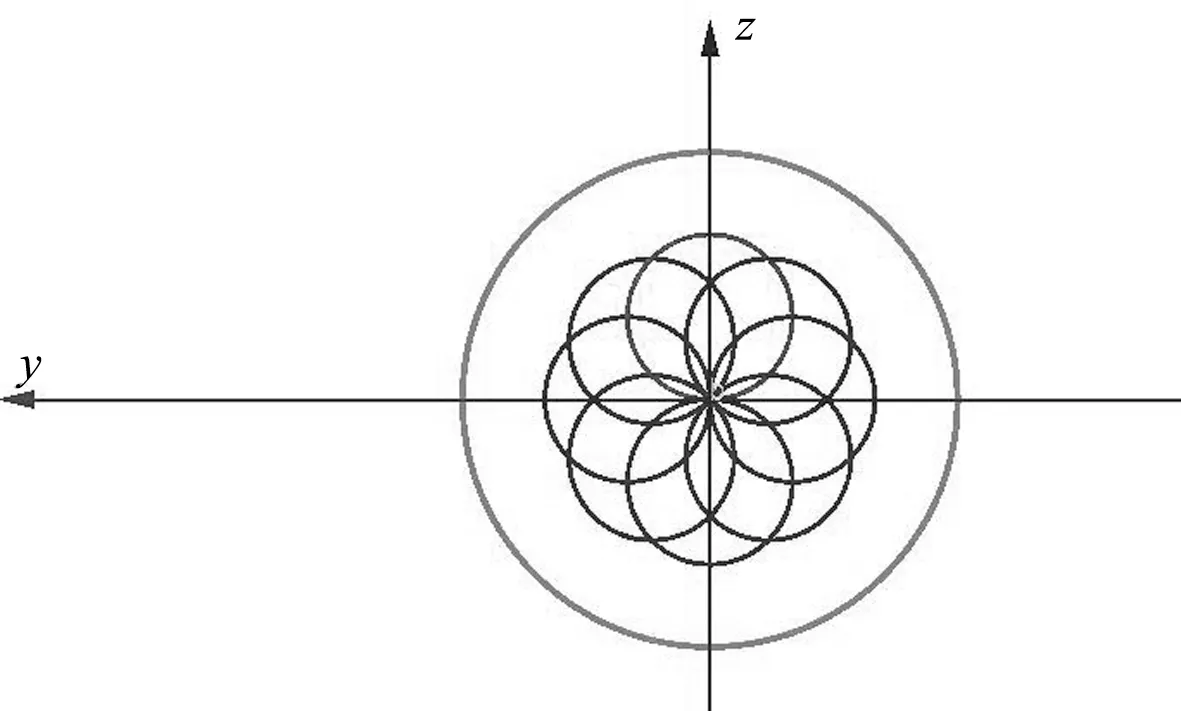
图10 半径大小关系

又题中

由式（3）～（5）可得

制作方法：

（1）密绕线圈也是等距螺旋线，其指令为：曲线（k，1.5sin（20πk），1.5cos（20πk），k，0，10）.

（2）得到粒子轨迹的指令为：曲线（t，0.5sin（0.2nπt），0.5-0.5cos（0.2nπt），t，0，10），其中n为滑动条，表示题中环绕周数，以上指令只能得到一条轨迹a，要获得多条轨迹可用“序列”和“旋转”两指令，其表达式为：序列（旋转（a，-k*45°，x轴），k，1，7，1）.

4 等距螺旋面

在Geo Geb ra软件中可以通过旋转曲面的方法将等距螺旋线旋转成等距螺旋面.

【例3】在街头的理发店门口，常可以看到这样一个标志：一个转动的圆筒，外表有红蓝相间螺旋斜条纹，我们感觉条纹在沿竖直方向运动，但条纹实际在竖直方向并没有升降，这是由圆筒的转动而使我们的眼睛产生的错觉.如图11所示，假设圆筒上的条纹是围绕着圆筒、连续的一条宽带，同种颜色相邻两条纹在沿圆筒轴线方向的距离（即螺距）为L=10 cm，圆筒沿逆时针方向（从俯视方向看），以2 r／s的转速匀速转动，我们感觉到升降方向和速度大小分别为（ ）

A.向上 10 cm／s

B.向上 20 cm／s

C.向下 10 cm／s

D.向下 20 cm／s

答案：B.

解析：由圆筒沿逆时针方向转动知我们感觉到条纹在沿竖直方向向上运动，圆筒转动一圈，用时0.5 s，感觉到条纹沿竖直方向向上运动L，因此向上运动的速度为20 cm／s.

制作方法如下.

（1）指令栏输入：曲线（cos（πk+α），sin（πk+α），8-2k，k，0，4），得到曲线a，表达式中α为表示角度的滑动条，启动α的动画功能可看到曲线a的旋转.

（2）指令栏输入：曲面（a，90°，z轴），得到曲面b为等距螺旋面，曲面b可随曲线a旋转.

（3）指令栏输入：旋转（b，π，z轴），得到同样可随曲线a旋转的曲面b′表示另一宽条纹.

（4）利用圆柱体工具按以上尺寸画圆柱体（半径取0.99）以表示圆筒，如图12所示.