“活泼”的追击问题——对第33届全国物理竞赛预赛题的思考

骆兴高

（杭州第十四中学 浙江 杭州 310006）

倪国富

（浙江省柯桥中学 浙江 绍兴 312030）

【题目】一足球运动员甲自A点向球门的B点踢出球，已知A和B之间的距离为s，球自A向B的运动可视为水平地面上的匀速直线运动，速率为u.另一足球运动员乙到AB连线的距离为l，到A，B两点的距离相等.运动员甲踢出球后，运动员乙以匀速v沿直线去拦截该球.设运动员乙开始出发去拦截球的时刻与球被运动员甲踢出的时刻相同.

（1）如果运动员乙能拦截到球，求运动员乙开始出发去拦截球直至拦截到球的时间间隔、球被拦截时球到A点的距离、球到运动员乙出发点的距离和运动员乙运动的方向与A和B连线的夹角；

（2）求为了使运动员乙能拦截到球，u，v，s和l应当满足的条件.

评卷时竞赛委员会提供的参考答案如下：

（1）记运动员甲踢出球的时刻为零时刻.设运动员乙沿着与A和B连线夹角为θ的方向运动，球在时刻t被运动员乙拦截.令球被拦截时球到A点和运动员乙到出发点的距离分别为s1和s2，则

由几何关系有

从式（3）、（4）消去θ，并利用式（1）、（2）得

这是关于t的一元二次方程.解为

由式（1）、（2）、（7）得

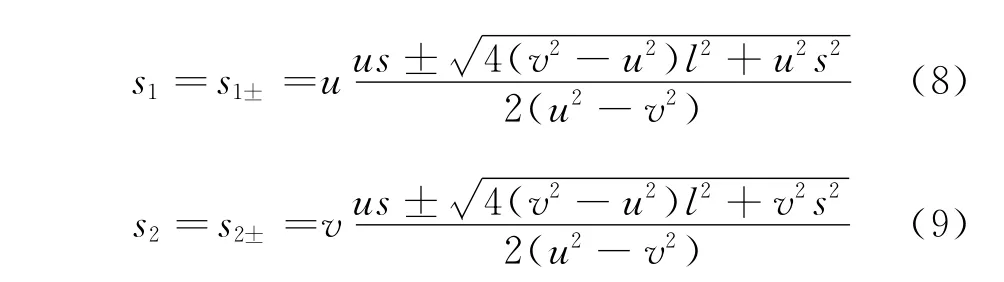
由式（4）、（9）得

（2）方程（6）有实数解的条件是

它是自动满足的.综上所述，式（12）、（14）、（15）即运动员乙拦截到球的条件.

当式（12）中大于号成立时，运动员乙可在两处拦截到球；当式（12）中等号成立时

运动员乙只能在一处拦截到球.

参考答案流程看下来类似于代数运算，并且解答过程不仅不完整且有误区，题目的本身是开放的，球运动速率u和足球运动员追击速率v之间的大小关系题中并没有明确，应考虑各种可能性，事实上笔者阅卷时发现参赛学生几乎没有按以上解题思路，阅卷老师对参考答案也提出了不少质疑，笔者认为完整的解答应按如下几种情形讨论：

如果以球为参考系，那么球是静止的，运动员乙在向球运动，乙在球的参考系中，既有向左的速度u，又有对地参考系中的速度v，u和v的合速度v21指向A.

如图1所示，图中α为运动员乙在初始位置时与运动员甲连线和AB之间的夹角，θ为运动员乙运动方向与运动员乙在初始位置时与运动员甲连线之间的夹角.

图1 以球为参考系时，运动员乙的运动

第1种情形如图2所示，当v＞u时，usinα=vsinθ，sinθ=，令球被拦截所需时间为t，则

图2 v＞u时情形

题中明确要求运动员乙运动方向和AB之间的夹角，即图中的β.因此原参考解答中仅用θ表示方向值得商榷的，应表述为

第2种情形如图3所示，当v=u时，θ=α

图3 v=u时情形

第3种情形如图4所示，当usinα＜v＜u时

图4 u sinα＜v＜u时情形

第4种情形如图5所示.

图5 v=u sinα时情形

当v=usinα时，即

第5种情形v＜usinα，如图6所示，无解.

图6 v＜u sinα时情形

分类讨论是一种重要的物理思想，如果面临的问题不能以统一的同一种方法处理或同一种形式表述、概括，那么就需要把一个复杂的问题按一定的标准分割成若干个简单的问题（本文中的标准能拦截到球），再逐一分析解决，得出每一类的相应结果，再综合各结果，得到最终答案的一种思想方法，也是近几年物理竞赛考题的一大热点［1，2］.