2021 年高考“空间几何体”问题聚焦

■向洪标

下面以2021年高考题为载体,探究空间几何体中经典问题的类型以及求解的思维方法,希望对同学们的学习有所帮助。

聚焦1：多面体表面积或体积的计算

例1 (2021 年新高考卷)正四棱台的上,下底面的边长分别为2,4,侧棱长为2,则其体积为( )。

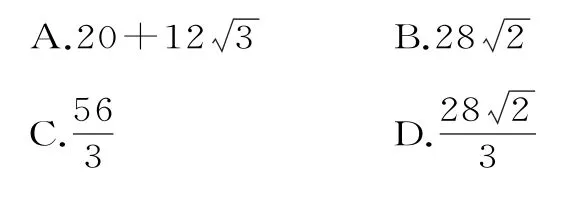
解：由正四棱台的几何特征可得该几何体的高及上,下底面的面积,再由棱台的体积公式即可得解。

作出图形,如图1所示。

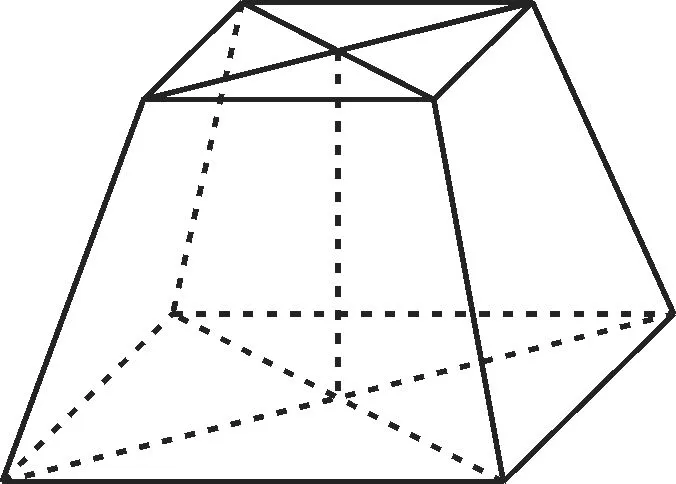
图1

回味：计算柱、锥、台体的体积,关键是根据条件找出相应的底面面积和高,应注意充分利用多面体的截面,特别是轴截面,将空间问题转化为平面问题求解。

聚焦2：旋转体的表面积或体积的计算

例2 (2021 年高考北京卷)定义:24h内降水在平地上积水厚度(mm)来判断降雨程度。其中小雨(＜10mm),中雨(10mm～25 mm),大雨(25 mm ～50 mm),暴雨(50mm～100mm),小明用一个圆锥形容器接了24h的雨水,如图2,则这天降雨的等级是( )。

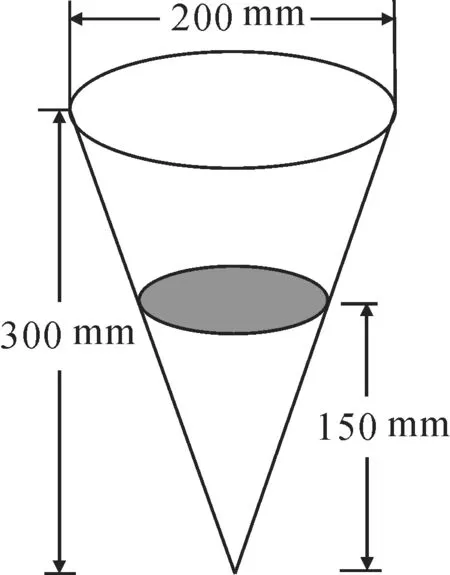
图2

回味：借助降雨程度,将问题转化为圆锥的体积与圆面积的有关计算。本题主要考查数据收集与处理、数学运算、直观想象等数学素养。

聚焦3：多面体的外接球的体积计算

例3 (2021年高考全国卷)已知A,B,C是半径为1的球O的球面上的三个点,且AC⊥BC,AC=BC=1,则三棱锥O-ABC的体积为( )。

解：根据截面△ABC的外接圆,确定小圆的圆心及半径,再根据球半径、小圆半径、小圆圆心到球心的距离,得到球心O到平面ABC的距离,最后求得体积(图略)。

因为AC⊥BC,AC=BC=1,所以

回味：解答本题的关键是明确球心和三角形外接圆的圆心的连线必垂直于三角形所在的平面。求多面体的外接球的表面积或体积的两种常用方法:三条棱两两互相垂直时,可恢复为长方体,利用长方体的体对角线为外接球的直径,求出球的半径;利用直棱柱的上下底面平行,借助球的对称性,球心为上下底面外接圆的圆心连线的中点,再根据勾股定理求出球的半径。

聚焦4：空间位置关系的判断

例4 (2021年高考浙江卷)如图3,已知正方体ABCD-A1B1C1D1,M,N分别是A1D,D1B的中点,则( )。

图3

A.直线A1D与直线D1B垂直,直线MN//平面ABCD

B.直线A1D与直线D1B平行,直线MN⊥平面BDD1B1

C.直线A1D与直线D1B相交,直线MN//平面ABCD

D.直线A1D与直线D1B异面,直线MN⊥平面BDD1B1

解：利用正方体间的垂直、平行关系进行证明。由正方体知A1D⊥AD1,A1D⊥AB,所以A1D⊥平面ABD1,所以A1D⊥D1B。在正方体ABCD-A1B1C1D1中,M是A1D的中点,N是D1B的中点,所以MN//AB。因为MN⊄平面ABCD,AB⊂平面ABCD,所以MN//平面ABCD,A 正确。由正方体知A1D与平面BDD1相交于点D,D1B⊂平面BDD1,D∉D1B,所以直线A1D与直线D1B是异面直线,B,C错误。因为MN//AB,AB不与平面BDD1B1垂直,所以MN不与平面BDD1B1垂直,D 错误。应选A。

回味：熟练掌握正方体中的垂直、平行关系是解题的关键,如正方体的两条棱平行或垂直,同一个面上的对角线互相垂直等。

A.3π B.4π C.9π D.12π

提示：如图4,设两个圆锥的底面圆的圆心为D,设圆锥AD和圆锥BD的高之比为3∶1,即AD=3BD。

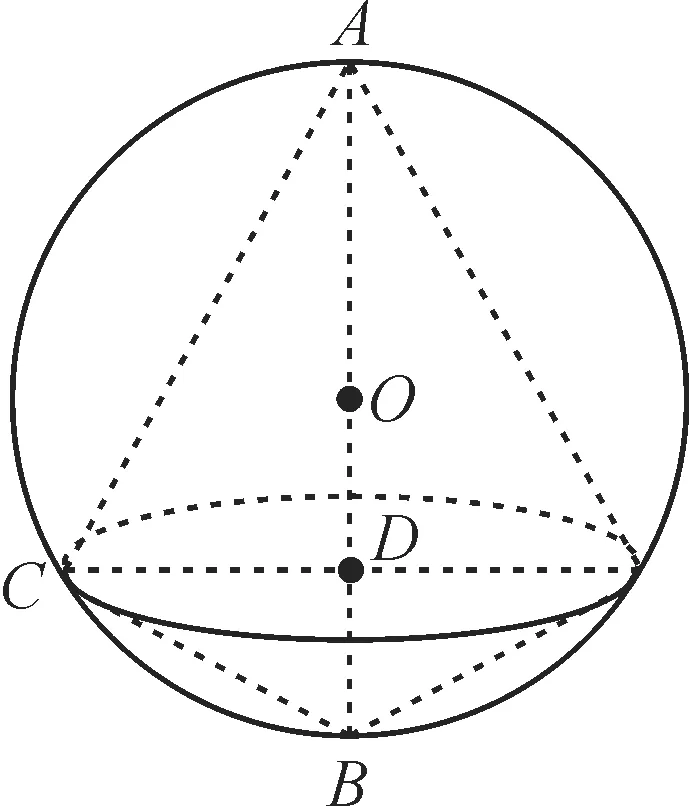
图4