太阳能二次聚集器聚光性能研究

谢林毅， 戴贵龙， 陈雪淇， 庄莹

(福建工程学院 生态环境与城市建设学院, 福建 福州 350118)

太阳能作为一种清洁无污染零排放的能源，可以解决现阶段人类能源巨大需求和环境保护之间的矛盾[1-3]。在吸热器太阳光入口布置二次聚集器，与一次聚集器组成太阳能两级聚集系统，是提高太阳能热转换温度和效率、防止吸热器外壁面被高倍聚集太阳能流烧蚀的重要技术途径。近年来，太阳能二次聚集器技术成为太阳能高效热转换的研究热点。

在反射式二次聚集器方面，郑宏飞等[4]构造了一种由二级复合抛物面叠置组成的漏斗式太阳能聚光器。庄立强[5]设计了一种两级太阳光传输方案。张艳梅[6]使用ASAP软件发现旋转双曲面反射式二次聚集器聚光比更高，结构更紧凑。CHENG Qiang等[7]优化分析了能流密度均匀分布的非成像二级反射器(NIS)结构方案。王云峰等[8]提出了一种新型多平面镜线性组合太阳能聚光器系统。尹鹏等[9]针对平板型太阳能聚光器中出现的漏光问题，提出了无漏光聚光器的设计方法。常泽辉等[10]提出了一种新型槽式复合多曲面太阳能聚光器。VOUROS A等[11]优化设计了一种线性菲涅耳二次反射镜。BELLOS E等[12]研究了一种针对抛物线槽型集热器的辅助反射器。马玄等[13]通过实验研究得出了加装CPC的菲涅尔二次反射塔式太阳能聚光系统吸收器的最佳温度。综合文献可发现，通过优化(广义)三维CPC的光路反射传输途径，是提高太阳能热转换效率的发展趋势。

鉴于三维CPC曲面复杂难加工(实际的三维CPC曲面基本通过内接多块平面小镜拼接组成)，本文提出一种多棱台结构二次聚集器。通过建立抛物面聚集器与多棱台两级聚集器光路传输模型，结合ProE和TracePro软件，采用了蒙特卡洛射线踪迹法(Monte Carlo Ray Tracing Method, MCRTM)，对两级聚集器的太阳能聚集传输特性进行模拟分析，为反射式二次聚集器的发展优化提供技术支持。

1 光路传输物理数学模型

1.1 物理模型

抛物面聚集器与多棱台两级聚集器光路传输模型物理模型如图1所示。多棱台二次聚集器的太阳光入口布置在抛物面聚集器的焦平面上，中心与焦点重合。吸热器的入口与多棱台二次聚集器的太阳光出口位置重合。入射太阳光经抛物面镜反射，进入多棱台二次聚集器腔内，经多棱台二次聚集器腔壁镜反射，从出口穿出，进入吸热器被吸收利用。

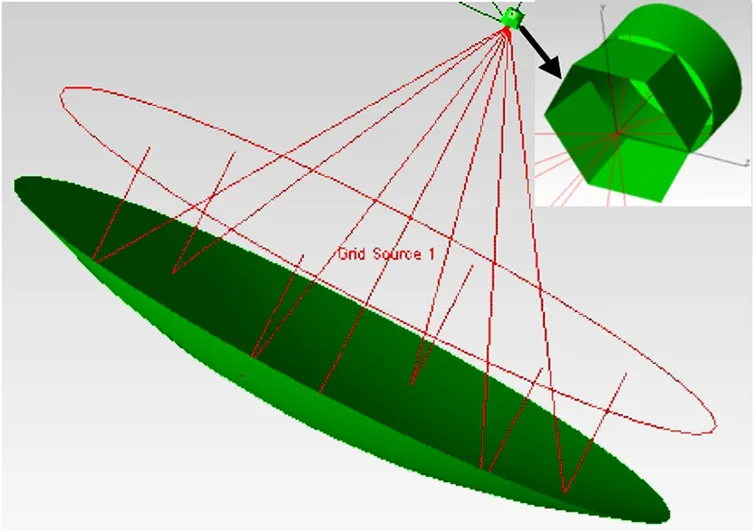
图1 抛物面与多棱台两级聚集器光路传输模型Fig.1 Optical path transmission model of the two-stage concentrator with a parabolic surface and a polygonal prism

在直角坐标系o-xyz中，抛物面的焦点在坐标原点(对称轴为x轴)，其表面方程为

(1)

式中，x、y、z分别为直角坐标系o-xyz中的x轴、y轴和z轴，f为抛物面的焦距，单位:mm。

抛物面聚集器的开口半径和高度计算式为

式中，ψ为抛物面的边缘角，即抛物面最边缘位置反射光线与对称轴的夹角，单位:(°)；R为开口半径，单位:mm；H为聚集器高度，单位:mm。

1.2 二次聚集器的光路模型描述

多棱台(四棱台、六棱台或八棱台)的侧壁为平面，其截面内的光路反射传输过程如图2所示。经抛物面聚集器反射的太阳光以圆锥的形式入射到多棱台二次聚集器的入口(圆锥半角等于抛物面的边缘角ψ)。多棱台的壁面倾斜角为α，点A为光学与一次入口直径的交点，点B为二次入口与光线的交点，点C为光锥对称轴与二次入口直径延长线的交点，点D为二次入口直径与多棱台壁面的交点。在ACD和ABC中，根据三角形几何关系，有CAD=α，BAC=ψ+2α。

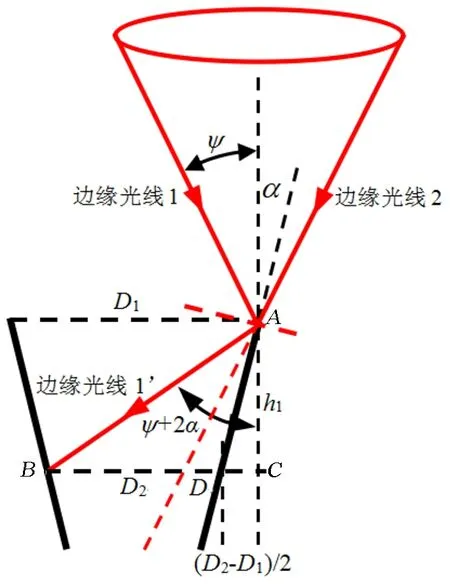
图2 多棱台二次聚集的截面光路传输模型Fig.2 Optical path transmission model of the cross-section of secondary concentration of the polygonal prism

(3)

(4)

式中，D1为棱台的直径，单位:mm；h1为光线第一次反射传输的深度，单位:mm；D2为出口直径，单位:mm。

联立式(3)和式(4)，可得出口直径D2计算式为

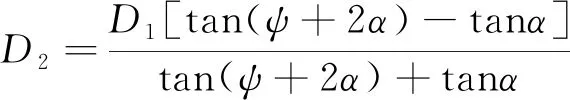
(5)

重复式(3)～(5)，可依次递推出每次反射的出口直径Dn+1

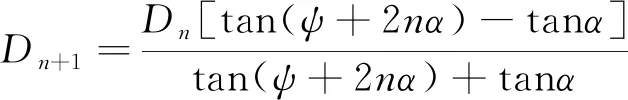
(6)

将式(5)代入式(3)可得第一次反射所需高度h1为

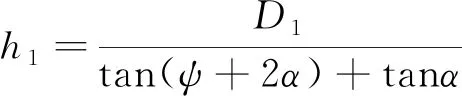
(7)

依次类推，可得第n次反射所需高度hn为

(8)

式中，D2为出口直径，单位:mm；Dn+1为反射第n次的出口直径，单位:mm；h1为第一次反射的高度，单位:mm；hn为第n次反射需要的高度，单位:mm。

已知抛物面的边缘角ψ(入射聚集光圆锥半角)、二次聚集器侧壁倾斜角α和多棱台的直径D1，结合二次聚集器内光线反射次数，即可计算hn，从而确定二次聚集器几何结构参数。

抛物面聚集器尺寸较大，在曲面加工和抛光过程中存在面型误差(实际曲面与理想曲线的差异)和镜反射误差(实际反射方向与理想镜反射方向的差异)，为方便分析，统一用光学误差表示[14]，有

(9)

式中，θs为太阳光锥半角，4.65×10-3rad；θsr为面型误差，取(1～8)×10-3rad；θmr为镜反射误差，取(1～5)×10-3rad。

结合ProE和TracePro软件，采用了蒙特卡洛射线踪迹法，模拟分析抛物面与多棱台两级聚集器的太阳光聚集传输特性，计算步骤概括为：

1)利用ProE软件建立结构相对复杂的多棱台二次聚集器、圆筒吸热器几何模型，如图3。

图3 Proe软件几何模型Fig.3 Geometric model of ProE software

2)将ProE建立好的几何模型导入TracePro软件，补充TracePro中自带的抛物面等模型，进行组装、调试。

3)定义一次聚集器、二次聚集器、圆筒壁和接收面材料光学属性(镜反射、漫反射以及吸收系数等等)。

4)建立光源模型(位置、形状、方向、光学误差)，通过设置光线发射面的圆环数调整跟踪光线数目。

5)光线追踪求解，根据追踪结果完成模型分析讨论。

2 结果分析

2.1 计算参数设置分析

模拟条件取：抛物面焦距f=3 000 mm，边缘角ψ=45°。圆筒吸热器，直径126.3 mm(与多棱台二次聚集器出口直径相当)，高度50 mm。圆盘光源，直径2 428 mm，在x=1 000 mm处，入射太阳光沿x负方向，能流密度为1 000 W/m2。跟踪光源数密度为107/m2(抽样环数约1 827)。太阳光锥半角为4.65×10-3rad，面形误差取5×10-3rad，镜反射误差取5×10-3rad，根据式(9)计算出光学误差为9.82×10-3rad，取10×10-3rad。一次反射面和二次反射面反射率为1，接收面吸收率为1。

二次聚集器为多棱台结构(四边形、六边形和八边形)，入口直径为150 mm(与抛物面焦斑半径相当)。当光线在多棱台腔内反射次数n=1时，求得出口直径为147.9 mm、高度为26.0 mm、聚光比为1.028；当光线在多棱台腔内反射次数n=2时，求得出口直径为126.3 mm、高度为61.0 mm、聚光比为1.411；当光线在多棱台腔内反射次数n=3时，求得出口直径为118.5 mm、高度为128.2 mm、聚光比为1.602(为保证光线持续向前传输，要求ψ+2nα<π/2，当取入口直径等于150 mm，ψ等于45°时，求得nα<22.5°)。从上述数据中可以看出，随着反射次数增加，尽管二次聚集器的聚光比略有增加，但是高度显著增加。综合考虑几何尺寸和聚光比，取n=2比较合适。对复合抛物面聚集器(三维CPC)，根据抛物面一次聚集器边缘角和焦斑半径，算得高度61 mm，出口直径126.3 mm，接收半角为23°[15]。如无特殊说明，上述计算参数保持不变。

2.2 模型验证

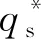
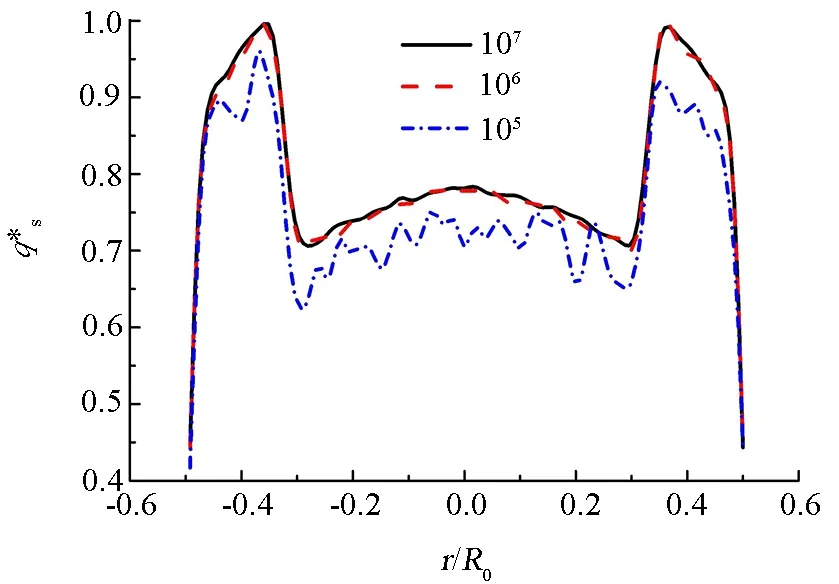
图4 六棱台跟踪光线数模拟结果Fig.4 Simulation results of the number of tracked rays by the hexagon prism

当光线数由105/m2增加到107/m2时，能流密度分布曲线逐渐变得光滑稳定。进一步分析发现，光线数为106/m2和107/m2时，两者的曲线分布几乎没有差异。综合考虑计算时间和结果精度，后续的计算工况，跟踪光线数取107/m2。

2.3 圆筒吸热器侧壁面能流密度图像分析

在TracePro中输入2.1中的参数进行模拟，四棱台、六棱台、八棱台以及复合抛物面两级聚集器的圆筒吸热器侧壁面能流密度分布特性如图5所示。由于圆筒吸热器的轴对称性，图5仅显示半个圆筒壁区域(圆周角θ为0～3.14 rad)。x=60 mm处为吸热器开口位置，x=110 mm处为吸热器底部)。

从图5中可看出，多棱台两级聚集器的侧壁太阳能流图像沿圆周方向为波浪型分布(图5(a)～(c))，波峰或波谷的位置靠近吸热器太阳光入口，且波峰或波谷的个数与等棱台的边或角相等，图5(a)的四棱台有4个峰，图5(b)的六棱台有6个峰，图5(c)的八棱台有8个峰(由于图5仅显示半个圆筒壁区域，峰的数量减半)。分析发现，能流图像的波浪型分布由多棱台的边角结构特性造成。多棱台的平面边与圆筒吸热器的侧壁存在较大缝隙，导致反射光线照射不到多棱台平面边背后的侧壁，导致吸热器侧壁能流图像出现波谷，而多棱台角坐落在圆筒侧壁上，反射光线能够照射多棱台角附近的侧壁区域，形成波峰。

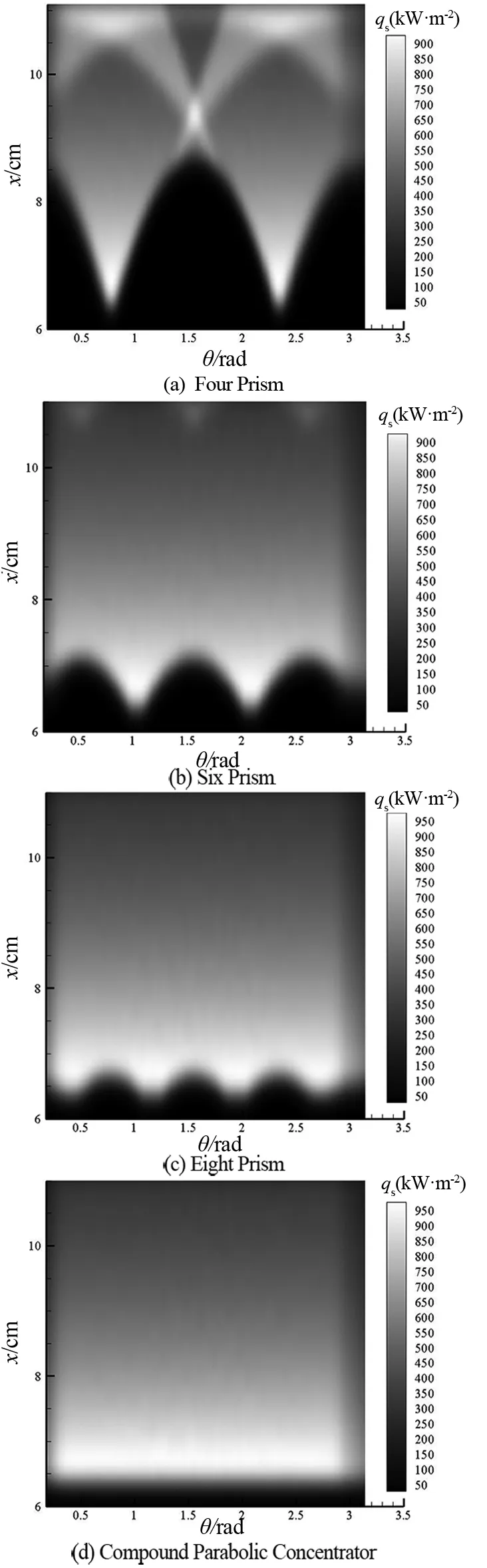
图5 两级聚集器圆筒壁太阳能流密度分布Fig.5 Distribution of solar energy flow density on cylinder wall of the two-stage concentrator

另一方面，太阳能流密度峰值一般位于图像的波峰上，且随着多棱台边数增加，太阳光聚集度增加，太阳能流密度峰值略有升高，四棱台的太阳能流密度峰值为939 kW/m2，六棱台的太阳能流密度峰值为964 kW/m2，八棱台的太阳能流密度峰值为969 kW/m2。

进一步分析可发现，四棱台二次聚集器，由于边数较少，对一次聚集太阳光的变异较大，导致吸热器侧面能流图像比较复杂，出现离散的多峰值分布特性，如图5(a)所示，在吸热器底部和中部也出现峰值，不利于布置工质换热系统。

对三维CPC，由于其旋转对称结构，在圆周方向太阳能流密度分布没有波动，比较均匀，且聚集度高，侧壁能流密度分布峰值约970 kW/m2。

2.4 吸热器入口平面太阳能流密度图像分析

多棱台两级聚集器的吸热器底面太阳能流密度分布特性如图6所示。从图6(a)～(c)可看出，在平面的边缘处，能流图像呈离散的多峰分布，峰的个数与多棱台二次聚集器的边或角的数量相等。能流图像峰值位于多棱台角的正上方，由角两侧的反射壁反射光线叠加形成。对比发现，随着多棱台边数增加，能流峰面积减小，峰值也相应降低，平面的中心区域能流密度逐渐增加，当多棱台由四棱台增加到八棱台时，相应的峰值由1 190 kW/m2降低到836 kW/m2。

图6 两级聚集器圆筒吸热器底面太阳能流密度分布Fig.6 Solar energy flow density distribution of the cylinder bottom ofthe two-stage concentrator

对三维CPC，如图6(d)所示，平面边缘的能流密度峰消失，呈现边缘区域能流密度低、中心区域能流密度高的近似高斯分布。

综合图5和图6可以发现，随着反射式多棱台二次聚集器的边数增加，沿圆筒吸热器的圆周方向，能流图像分布的峰值幅度逐渐减小，越来越平缓均匀。从能流图像性能来看，三维CPC是理想的反射式二次聚集器。但是三维CPC曲面复杂，加工技术难度大，成本高，多棱台二次聚集器，尤其是六棱台二次聚集器，聚光比适中，能流图像分布较均匀，容易多个拼接构成大型二次聚集器簇，具有良好的发展应用潜力。

3 结论

1)随着多棱台二次聚集器高度增加，光线在腔内的反射次数增加，聚光比相应增加。当光线反射次数为2时，入射边缘角为45°，3种多棱台二次聚集器的聚光比约1.4，为三维CPC(聚光比为2)的70%左右。

2)在圆筒形吸热器侧壁靠近太阳光入口处，多棱台二次聚集器的太阳能流密度呈波浪型多峰(谷)分布，且峰的个数与多棱台的边数相等；在圆筒形吸热器底面边缘处，太阳能流密度分布呈离散的多峰分布，峰由多棱台的折角反射光线重叠形成。

3)在圆筒侧面和底面的圆周方向，三维CPC两级聚集器的太阳能流密度分布相对光滑平整。但总体上，多棱台两级聚集器与三维CPC两级聚集器的太阳能聚集性能相当，是后者的有效替代技术。