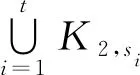不含H子图的图上的最大割下界

林晶12

(1. 福建工程学院 数理学院， 福建 福州 350118；2. 福州大学 离散数学研究中心， 福建 福州 350116)

给定一个图G，令f(G)表示G的二部子图包含的最大边数。给定一个正整数m，令f(m)表示所有具有m条边的图G的f(G)的最小值。经典的最大割问题旨在寻找f(m)的值，该问题有非常广泛的应用价值，被应用于复杂网络社团结构分析、大规模集成电路设计(VLSI)，同时也在统计物理学中用来研究处理自旋玻璃(Spin glass)状态的重要模型之一。

猜想0.1[7]. 对于任意给定的图H，存在常数ε(H)>0，使得f(m,H)≥m/2+Ω(m3/4+ε)。

提高猜想0.1中下界的误差项非常困难，即使相对简单的图H。到目前为止，引起国内外学者最广泛研究的情况是H=K3。在诸多研究[8-10]之后，Alon[2]证明了对所有的m，f(m,K3)至少是m/2+Ω(m4/5)，且这个下界是紧的。Alon, Krivelevich和Sudakov[11]进一步延伸了该结论：令H由单个顶点连接某一棵非平凡树的所有顶点构成的图，存在一个常数c=c(H)>0，使得对所有的m，均有f(m,H)至少是m/2+cm4/5，且这个界是紧的。最近，Zeng和 Hou对H是完全图的情形[12]和H是奇圈的情形[13]分别给出了相应的下界。

森林是不含圈的图，想进一步研究当H是由单个顶点连接某个含圈图的所有顶点构成的图时，f(m,H)的下界情况。在含圈图中，最典型的就是圈或完全二部图K2,s。因此，本文将考虑猜想0.1，当H是一个偶轮或者H是单个顶点连接任意多个不交的K2,s的所有顶点构成的图。无特别说明，本文中的图均为有限无向简单图，所有的对数均以e为底。设G和H是两个不交的图，将G和H的不交记作G∪H。

1 单点连接的情形

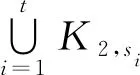
延续文献[2,7,11]中的讨论，并附加一些新的思想，需要用到一些已知的结论。首先，介绍下述引理，它在证明中起到至关重要的作用，揭示了一个染色数“较小”的图必包含一个“较大”的二部子图。详细证明可参考文献[2,7,11,14]。

下面的3个引理，分别用不同的参数给出了图G的f(G)的不同下界。

其次，介绍一个不含单边最大度大等于2的二部图的图的边数上界。

引理1.6[16]令H是一个二部图且它的其中一部分顶点的最大度为Δ′≥2。若G是一个有n个顶点且不含H的图，那么存在一个常数b=b(H)>0，使得e(G)≤bn1-1/Δ′。

最后，介绍一个引理，它阐述了对于具有相对大的最小度且每个顶点的邻居导出子图较稀疏的图来说，必存在某个满足指定条件的随机导出子图。

引理1.7[12]设G=(V,E)是一个有n个顶点、m条边且最小度为mα的图，其中α∈(0,1)是一个固定的实数。假设m充分大，且存在某个常数s>0,使得任意一个度为d的顶点v∈V,v的邻居的导出子图至多包含sd3/2条边。那么，对每一个常数η∈(0,1)，都存在一个G的导出子图G′=(V′,E′)，满足以下性质：

·V′中任意一个在G中度为d的顶点v，v的邻居在G′中的导出子图至多有2η2sd3/2条边。

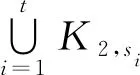
情况1 假设G中存在一个阶为N的顶点集U，使得U的导出子图G′=G[U]的最小度至少为q。显然，e(G′)≥qN/2。定义

其中，θ=θ(t)∈(0,1)是一个系数，它的值将在后面证明中给出。首先证明存在U′⊂U使得G′有一个U′的导出子图G″=G[U′]，G″至少包含qN/4条边且G″是O(r)-可染的。为得到这个结论，从U中均匀地随机选取2t个顶点，有放回地独立重复取r次，于是得到r个随机顶点集，记为X1,X2,…,Xr。假设Xi={x1(i),x2(i),…,x2t(i)}，1≤i≤r，令X={X1,X2,…,Xr}，则显然有|X|≤r。构造随机顶点集U′，将U中任意一个顶点u放入U′，当且仅当存在某个Xi∈X,使得{ux1(i),ux2(i),…,ux2t(i)}⊆E(G′)。从而得到G′的一个导出子图G″=G[U′]。

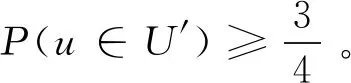
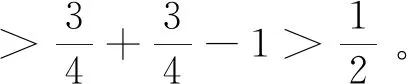
由于e(G′)≥qN/2且期望具有线性可加性，结合上式，得到

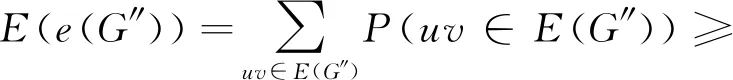
即G′中存在子图G″至少包含qN/4条边。

综上，找到一个随机顶点集X，|X|≤r，由X对应了一个子图G″⊆G至少包含qN/4条边且是O(r)-可染的。下面，证明f(G)的下界。若N≥m(2t+1)/(3t+1),那么由引理1.3，

上式结合引理1.4以及q的定义，得到

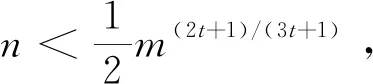
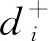
其中，δ=δ(G′)是视需要而取定的常数。上述不等式结合引理1.4，可以得到

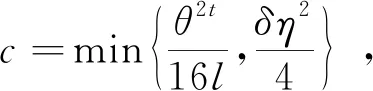
由定理1.1，可推出下述结论：

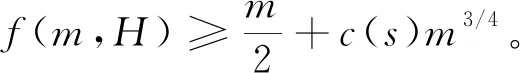
2 偶轮的情形

定理2.1令k≥2是一个正整数，W2k表示由单个顶点连接圈C2k的所有顶点构成的轮图。那么存在一个常数c(k)>0，使得对所有的m，均有

定理2.1的证明方法与上一节定理1.1的证明方法类似。介绍一个不含特定偶圈的图的边数上界。

引理2.2[17]假设k≥2是一个整数，假设G是一个有n个顶点且不含长度为2k的圈的图，那么G中至多有100kn1+1/k条边。

定理2.1的证明 假设k≥2是一个给定的实数，假设G=(V,E)是一个有n个顶点、m条边且不含W2k的图。因为C4=K2,2，所以由推论1.2可知，k=2时结论成立。因此下面假设k>2。定义q=m2k/(3k+2)，类似定理1.1的证明，根据G是否存在稠密子图，分两种情况进行讨论。

从U中均匀地随机取k个顶点，有放回地独立重复取r次，于是得到r个随机顶点集，记为X1,X2,…,Xr。记Xi={x1(i),x2(i),…,xk(i)}，X={X1,X2,…,Xr}。构造顶点集U′如下：将U中任意一个顶点u放入U′中，当且仅当存在某个Xi∈X,使得{ux1(i),ux2(i),…,uxk(i)}⊆E(G′)。令G″=G[U′]。那么对U中的一个固定顶点u，事件不存在一个Xi∈X使得{ux1(i),ux2(i),…,uxk(i)}⊆E(G′)的概率至多是

固定上述的集合X和U′，对任意Xi∈X，令Gi是Xi中所有顶点的公共邻居在G′中导出的子图。因为G中不含W2k，故每一个Gi中不含K1,k，从而Gi是2(k+1)-可染的，所以G″是2(k+1)r-可染的。

若N

假设N≥m(2k+2)/(3k+2)，由引理1.3，

3 结论

2)令H由单个顶点连接K2,s的所有顶点构成的图。那么存在一个常数c(s)>0，使得f(m,H)≥m/2+c(s)m3/4。

3)设k≥2是一个正整数，W2k表示由单个顶点连接圈C2k的所有顶点构成的轮图。那么存在一个常数c(k)>0，使得f(m,W2k)≥m/2+c(k)m(2k+2)/(3k+2)。