基于多分辨率动态模态分解的电磁信号时频-能量分析
郑建拥, 魏光辉
(陆军工程大学石家庄校区电磁环境效应国家重点实验室, 河北 石家庄 050003)
0 引 言
由于现代电子产品如5G手机、虚拟现实和物联网的发展和普及,电磁环境变得非常复杂。伴随而来的复杂电路系统,包括非线性元件、不连续结构和复杂的激励信号,会遇到串扰、辐射泄漏、高次谐波以及由此产生的非线性电磁辐射等问题,已经成为射频干扰和宽带辐射杂散发射的噪声源。通常,这些信号和辐射只能被记录和呈现为时域或频域信号,而环境中电磁辐射的动态变化也对信号处理和工程技术提出了高要求。因此,正确实时分析和解释电磁辐射的更多物理特性具有重要意义。为了解决这一问题,学者们提出了一种对传统扫频测量的频率数据进行傅里叶反变换的频域瞬态建模方法。然而,这种方法需要在频域和时域分辨率之间进行权衡,通常需要大量的测量时间才能达到预期的效果。为了解决这一问题,出现了几种时域电磁干扰(electromagnetic interference,EMI)测量系统,利用数字信号处理技术减少测量时间,如模拟数字转换器和数字示波器。这些时域EMI测量系统具有多分辨率、全频谱、省时、低成本等优点。随后,经验模态分解,也被称为Hilbert-Huang变换,将时变数据集分解为几个内在模态函数,提供对测量结果的物理解释。然而,由于时域测量方法的限制,对保留信号完整性至关重要的辐射场空间信息丢失了。随着时域数值方法和先进的空间实验技术对电磁辐射、时变辐射场数据的高空间分辨率分析的发展,学者们开发了基于空间特征提取来定义物理特征辐射的领域。尤其是,奇异值分解可以从微带线的辐射场中提取模态,其中每个模态由特征幅值来区分。还有研究将奇异值分解和时域有限差分相结合,可以提取出所有可能的传播模态和倏逝模态而不需要有复杂三维结构的先验知识。然而,上述空间分析方法中丢失了时域信息,因此在分解的结果中没有明确的时间物理意义。
针对这些信号分析方法时-频-空间不兼容的问题,动态模态分解(dynamic mode decomposition,DMD)被开发出来。DMD来源于库普曼理论和动力系统的结合,是一种无方程的、数据驱动的方法,可以在短时间内对复杂系统中的时空相干结构进行评估甚至预测,已成为一种处理时空信号的新工具。DMD方法的核心是将本征正交分解(proper orthogonal decomposition,POD)这一空间降维技术与时域傅里叶变换相结合。更准确地说,DMD方法在数据收集范围内生成一个线性动力系统的最小二乘回归。在具有可观测状态的动态系统中,基于局部线性假设,该方法可以得到动态系统的主模态及其变化规律。该方法通过低维分解状态来捕捉非线性动力场的主要特征,产生非线性偏微分方程的可观测值,并在全球电力系统和大规模神经记录中提取显著的时空模式。但是在诸多研究中,DMD多用于流体动力学、振动力学等动力学领域,而在电路和电磁辐射信号分析等电动力学方面,并没有很深入的研究。在射频信号分析方面也没有时空耦合的分析方法。
同时,在时间和空间上的多尺度系统建模,已经渗透到工程、生物和物理科学的现代理论和计算工作中。数据驱动的创新方法和算法规避了连接微观和宏观尺度效应的重大挑战。这种多分辨率分析(multi-resolution analysis, MRA)一般是基于小波变换或加窗傅里叶变换来执行的。Kutz整合了DMD分解与小波理论,将MRA的概念与最近兴起的DMD相结合,提出一种产生低维时空模态的技术,提出的多分辨率DMD(multi-resolution DMD, mrDMD)能够自然地整合空间和时间,方便地分离多尺度时空特征,并建立近似的动力学模型。
mrDMD兼具DMD的所有优点。首先,不需要神经网络方法所要求的训练过程,避免了神经网络所需的大量数据和训练时间。其次,这种纯数据驱动的方法不受时频分辨率限制,可以实现基于数据的实时分析。第三,提取的DMD频谱和动态模式分别在时域和空间域提供了明确的物理意义。最后,提出的方法可以降低维数。分解后的动态模态中已经包含了线性和非线性系统的主要特征。mrDMD最显著的改进,是增强了频率捕捉的能力,并且在医学检测、图像处理、非线性分析等领域取得了良好的成果。但在电磁领域,还没有相关应用。
本文首次将mrDMD引入到电磁信号分析领域,在mrDMD的基础上结合时频分布,提取各模态瞬时能量特征,并对电磁辐射信号进行分析。且首次从时-频-空间-能量4个方面多角度动态侦测电磁环境,解决了电磁信号时-频-空间-能量分析不兼容的问题。这个新方法可以为大规模EMI分析提供强有力的工具。
1 DMD理论基础
DMD方法将时空相干的数据分解为一组动态模式,这些动态模式来源于给定系统采集的数据快照或测量结果。数据收集过程涉及两个参数:,每个时间快照的空间测量的数量;,时间快照的数量。DMD中时间快照的间隔可以是不规律的,但是为了叙述方便,设定快照间隔的时间相等:
=-1+Δ
(1)
式中:采集时间开始于,结束于;为整数计数单位,Δ为数据采集时间间隔。在mrDMD方法中,由于算法提取的是多时间尺度时空结构,快照总数会发生变化,数据快照被排列成一个×矩阵。这将在下一章详细解释。
=[(),(),…,()]
(2)
式中:向量为维列向量,是在数据采集点上感兴趣的系统状态变量的个测量值,目的是挖掘数据矩阵中重要的动态信息。接着,截取中的一个×分矩阵,定义为
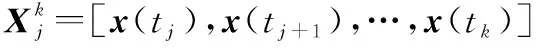
(3)
DMD方法近似于所谓的库普曼算子的模态。库普曼算子是一个线性的、无限维的算子,具体的过程是对其最佳拟合线性算子的特征分解进行近似,该算子将时刻的状态与下一个时间的状态+1相关联:
+1≈
(4)
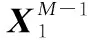
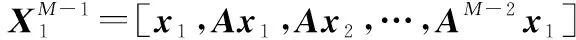
(5)
由此,式(4)可以写成如下形式:
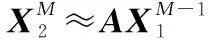
(6)

相反地,DMD通过应用基于POD投影矩阵的秩约化表示来绕过的特征分解。DMD算法具体如下。
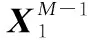
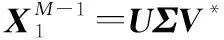
(7)
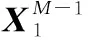
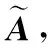
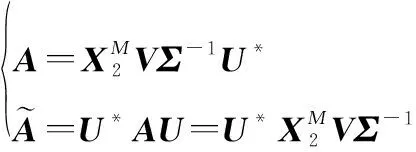
(8)
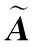
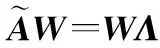
(9)
式中:的列是特征向量;是包含相应特征值的对角矩阵。
最后,可以从和中重建的特征分解。的特征值由给出,的特征向量(即DMD的模态)由列给出:
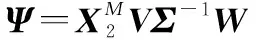
(10)
得到所有特征值和特征向量以后,就可以构造未来所有时间的预测解。为了方便,首先重写=ln()Δ,然后给出所有未来时间的近似解():
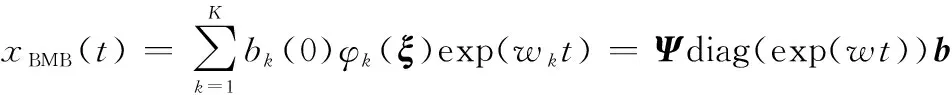
(11)
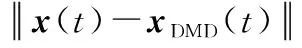
现在只剩下计算初始系数值(0)。如果考虑=0时刻的初始快照,那么结合式(11)得出的=,通常不是一个方阵,所以其解一般表示为
=
(12)
式中:表示在Matlab中通过pinv命令解出的Moore-Penrose伪逆。伪逆等价于在最小二乘(最佳拟合)意义上找到最佳解决方案。到此,完成DMD的基本推导。
2 mrDMD
mrDMD的灵感来自于视频处理和传输中分离慢模块和快模块的技术,其可以递归地从给定的快照集合中分离出低频或缓慢变化的内容。一般来讲,需要合适地选择快照的数量,以便DMD提供所采集到的动态数据的近乎全秩的近似模态。因此,可以选择,使所有的高频和低频内容都存在。在mrDMD中,最初以同样的方式选择,这样就可以完成一个近乎全秩的近似。从这个初始的数据传递过程中,最慢的模态被分离出,然后数据域被分成两部分,每部分有/2个快照。之后还会对这两部分的快照再次执行DMD。再次分离出最慢的模态,并继续执行算法,直到期望的终止。在数学上,mrDMD在第一轮DMD过程如下:
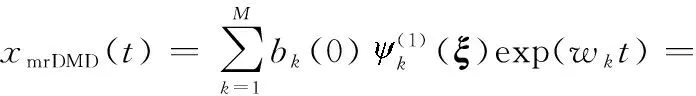
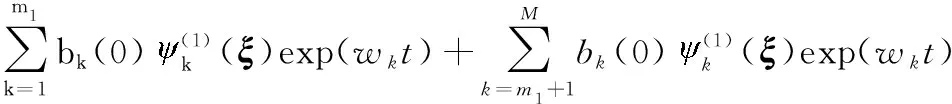
(13)
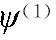
式(13)中的第一个和表示慢模块动态,而第二个和是所有其他的。因此,可以计算第二个和,得到矩阵:
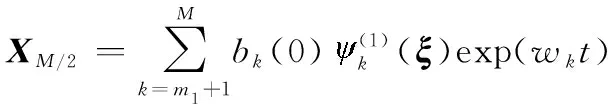
(14)
接着,在2上进行第二轮DMD分解,主要注意的是,2已经被分为两部分:
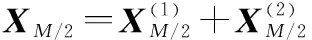
(15)
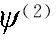
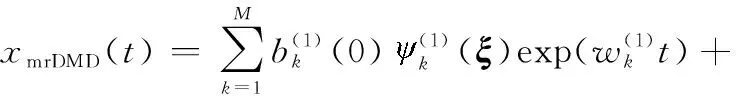
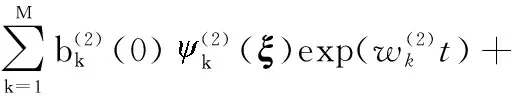
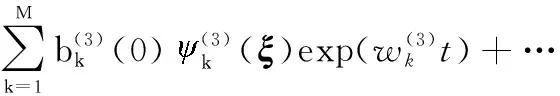
(16)
3 时频分布
近年来,时频分析在信号处理领域受到了广泛的关注。时频处理方法是将信号显示在一个完整的空间中,可以提供更多的信号信息,是结合频域和时域发展起来的信号处理方法,而且这些方法在非平稳信号处理中更为实用。但是,目前信号的振幅或功率谱不能提供信号频率如何随时间变化的信息,而这一信息对于调频或非平稳信号非常重要。尤其是目前工程技术要求实时分析变化的电磁信号的多种特征信息。
为了使mrDMD能更进一步地提取电磁信号的能量特征,采用蔡氏分布(Choi-Williams distribution,CWD)方法观察所有模态的时频分布:
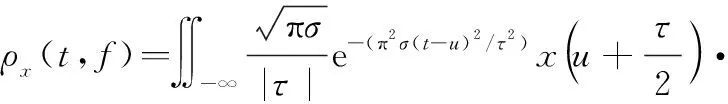

(17)
的值指定了在时间-频率平面上去除重叠部分的剩余信号的数量。研究表明:
(1) CWD是实值;
(2) 信号在时间(或频率)上的移位导致相应的分布移位;
(3) 在每个频率上所有时间的CWD的积分等于该频率上信号的频谱密度;
(4) 每一时刻的CWD对所有频率的积分为该时刻的瞬时功率;
(5) 在整个(,)平面上的积分等于总信号能量。
需要注意的是,在时频域检测信号的特性比单独在时域或频域检测信号的特性要容易得多。为了提取电磁信号的时-频-能量这3种相互关联的特征信息,沿时间轴和频率轴的时频平面,将整个平面划分成不同的区域,然后通过积分可以获得每个区域的能量随时域(频域)动态变化的具体过程。CWD可以详细描述沿时间轴、频率轴和整个时频平面的能量变化,而能量变化的细节更能提供有用的信息。而整体特征,例如时频平面的总能量,可以通过求和获得,也可以为电磁信号分析提供一部分参考。
具体而言,首先将时频平面划分为小的、相等的窗口,然后计算每个窗口的能量(,其中和分别表示沿时间和频率的坐标)。这些能量归一化后的总和为时频平面的全部能量。对信号细节的分析具体可以通过调节小窗口的大小和数量来掌控。而沿不同方向的积分(时域轴和频域轴)可以获得不同类型的信号特征信息。
4 仿真实验
为验证本文的方法,利用Matlab的simulink工具箱,建立了两个方向正交、频率不同的二维时空耦合的射频电磁信号模型,并在加入高斯白噪声后合成混合信号,通过上述方法流程进行处理。
信号1沿轴正方向传播,设置为10 ns。的频率设置为100 MHz,其公式如下:
=sin(-2π)cos(2)exp()
(18)
信号2沿轴正方向传播,的频率设置为50 MHz,其公式如下:
=sincos(2-π)exp()
(19)
两个信号的动态传播演示如图1所示,分别截取了总信号和两个分信号一个周期的传播形态。

图1 仿真信号动态演示Fig.1 Dynamic demonstration of simulated signal
需要注意的是,图1中代指各信号周期,不代表具体时间。接下来对总信号进行mrDMD处理,分解后的前三阶模态如图2所示。
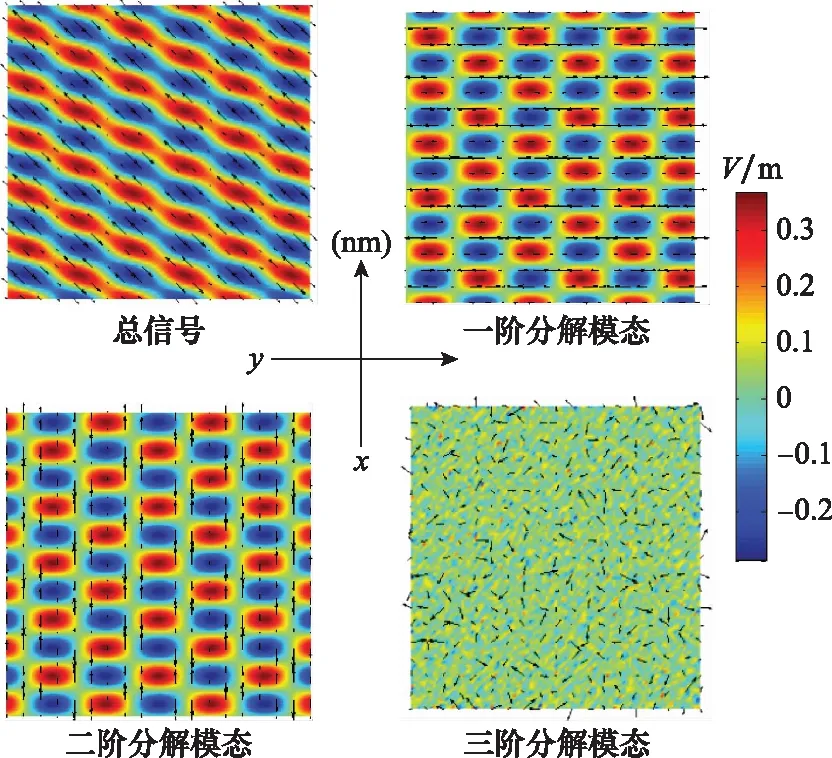
图2 mrDMD结果Fig.2 Results of mrDMD
需要注意的是,图2中黑色箭头代表的是电磁波的传播和振动方向。如图2所示,mrDMD清晰地将不同频率和不同方向的两个时空耦合信号分离开来,而第三阶分解模态代表了高斯噪声。
图3是经过CWD的总信号时频分析结果。图4是经过CWD的两个分信号时频分析结果。可见,mrDMD对两个信号和噪声的分离效果比较理想。结合图3和图4,可以采集更多电磁信号的时-频-能量信息。
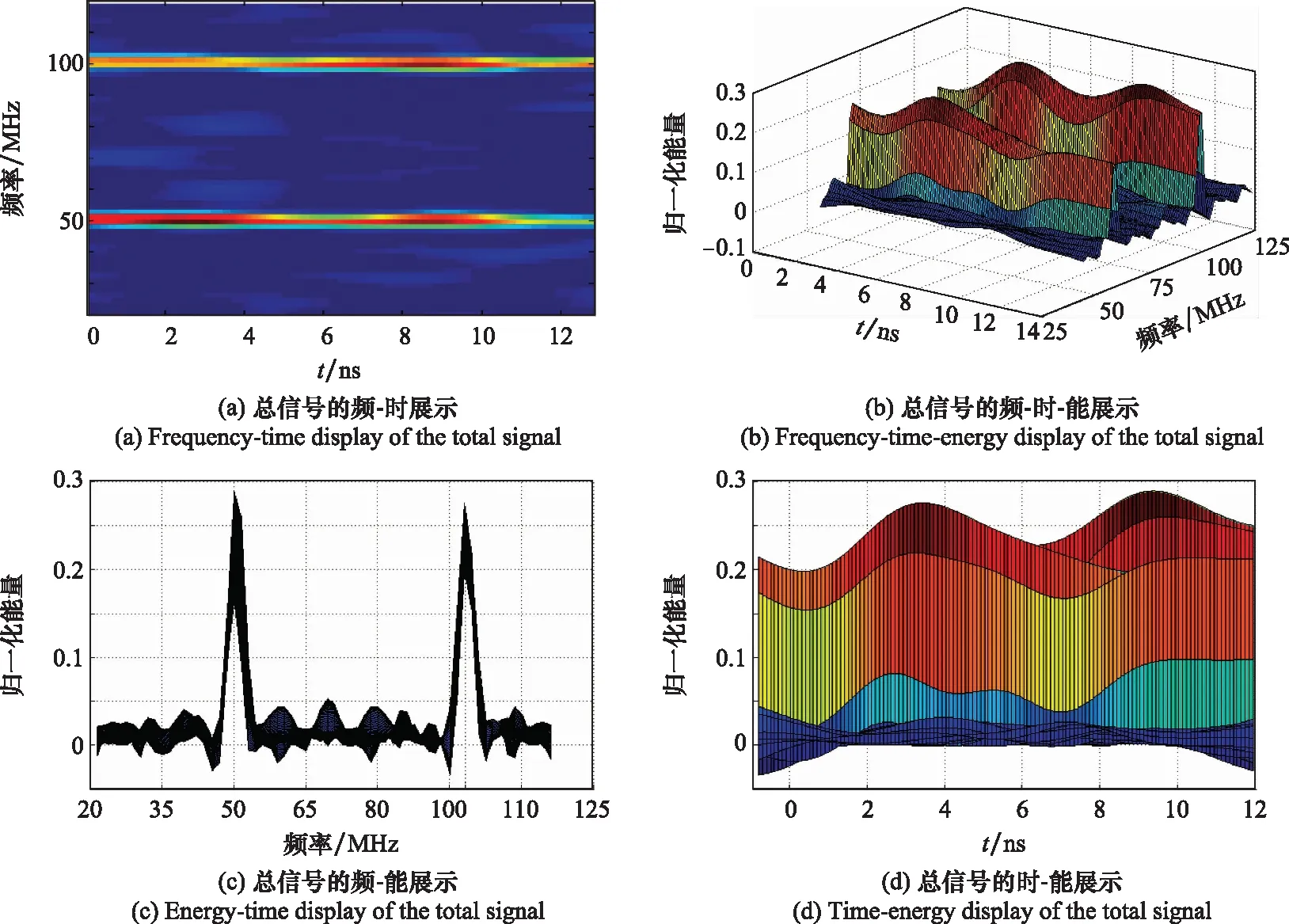
图3 总信号CWD分析结果Fig.3 CWD analysis results of total signal
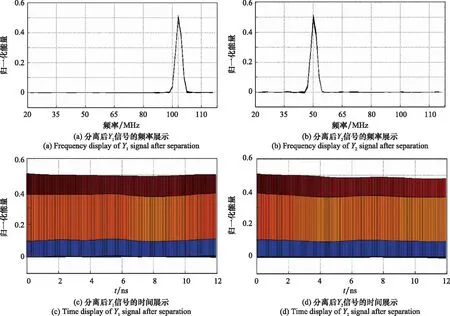
图4 两个分信号CWD分析结果Fig.4 CWD analysis results of two subsignals
为了定量理解所提出方法的精度,使用均方误差(mean squared error, MSE)函数作为误差指标:
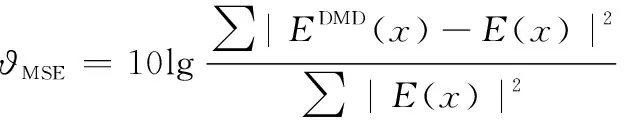
(20)
式中:()为实际电磁信号(场)的强度;()为DMD分解后重组或者预测的电磁信号(场)强度;将两个分信号组合后得到重构信号,并计算重构信号和实际信号的MSE,如图5所示,MSE的平均值在-18 dB以下,验证了方法的良好效果。第5 ns时,MSE最大的误差主要来自仿真中的数值误差和分解中的残差误差。
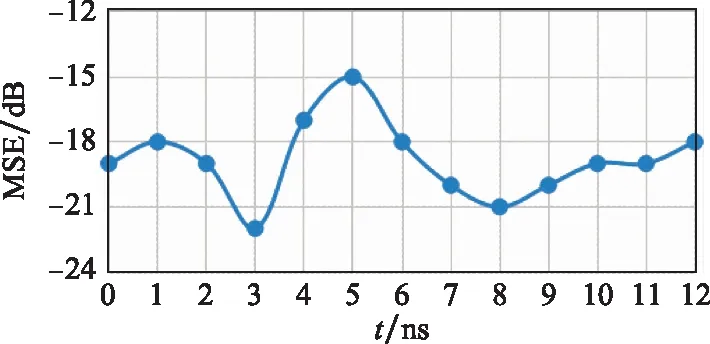
图5 重组信号和原信号的MSEFig.5 MSE of the recombinant signal and the original signal
需要注意的是,mrDMD要求每个时间快照保存的空间点的数量应该大于快照的数量,且mrDMD在观察时需要等间隔的时间采样。另外,观测中的噪声会干扰式(8)中的矩阵,使分解结果失真,从而使预测或重组的性能变差,对于长时间预测尤其如此,而且mrDMD方法只适合于分析非平稳电磁信号。此外,DMD方法可以看作是库普曼算子的有限维近似,其中观测函数是数据本身。因此,在DMD方法中重建和预测的效果完全依赖于数据,这也就对信号的探测和采集提出了更高的要求。
5 结 论
以精确、实时的分析电磁信号的时空-频率-能量特征,适应目前动态变化的电磁信号分析的工程要求为目的,首次提出了对电磁射频信号进行多重特征分析。采用mrDMD和CWD分析方法,对电磁信号的时间、空间、频率、能量特征进行了采集。可得出以下结论:
(1) mrDMD可以有效地分离出时空耦合的不同频率的射频电磁信号和噪声,并且可以精确地捕捉信号的运动状态;
(2) CWD视频分析技术可以应用于mrDMD分解出的模态的时频分析,在时-频-能量特征的采集方面具有比较理想的效果;
(3) 仿真实验结果证明了提出的电磁射频信号时空-频率-能量分析方法的可行性,可以为抗电磁干扰提供一定工程参考。

