基于车辆传感识别简支梁桥损伤的位移曲率法研究*

王珊珊 肖志全 亓兴军 亓圣

1.山东高速集团有限公司 济南250098 2.山东建筑大学交通工程学院 济南250101

引言

随着桥梁服役年限的增加，由于车辆重载、风化或自然灾害，导致桥梁结构的刚度下降，甚至影响其正常使用。根据2021年5月交通运输部发布的《2020年交通运输行业发展统计公报》，2020年末全国公路桥梁已达91.28 万座，随着桥梁数量大幅增加，迫切需要发展方便有效的技术来检测桥梁的损伤，以便提供高质量和高效的维修［1－4］。

大多数测试方法都需要在桥上安装大量的传感器来检测模态特性，如频率、模态振型和阻尼系数，它们被称为直接方法，模态特性是直接从桥的振动数据中获得的［5］。直接测量法原理清晰，研究相对成熟，但是直接测量法仍存在以下缺点：经济性差，通常需要在桥上安装数据采集系统以及大量的传感器，部署复杂，后期维护成本高；产生大量的数据，即所谓的“海量数据”，可能无法有效消化并且加以利用；缺乏通用性，为一座桥专门设计的监测系统很难转移到另一座桥上并在那里正常工作，另外监测系统的寿命很难与桥同生命周期。

Yang 等［6］在2004年基于车桥耦合理论率先提出了通过车辆响应识别桥梁模态参数的“间接测量法”。其基本思路为车辆与桥梁由于耦合作用，桥梁的振动对车辆产生激励，提取车辆的竖向加速度响应，对车体加速度响应运用相关信号处理技术，能够分离出相应的桥梁频率信息。随后Lin等［7］在2005年通过现场试验验证了该方法的有效性，说明了间接测量法识别桥梁频率的可行性。

其后大量的学者基于间接测量法进行了相关拓展，主要是集中在实际应用中不利影响因素的探究、桥梁动态特性的间接测量、桥梁损伤识别等领域。

在提出间接测量法之后，杨团队在这一领域作为先驱，着重在基本概念和力学机理上推进该方法。基于间接测量法识别桥梁频率解析解公式，Yang等［8，9］在2014年对间接测量法做了进一步的拓展，利用希尔伯特变换识别出了简支梁桥的振型，并推导出了识别桥梁振型的解析解；同年，Malekjafarian等［10］通过数值模拟，采用奇异值分解技术和短时频域分解技术，利用分段构造桥梁模态的方法，识别出了桥梁的振型；2017年，Obrien等［11］利用两轴残差响应提取桥梁模态，提高了桥梁模态识别的精度。

基于桥梁模态和桥梁损伤的相关性［12－14］，利用识别出的桥梁模态进行损伤识别成为研究热点，He等［15，16］利用识别到的桥梁模态信息，识别出了桥梁的损伤位置；贺文宇等［17］在2018年基于间接测量法理论，在桥面平整条件下利用识别到的前两阶振型进行了损伤识别；阳洋等［18，19］在2019年基于间接测量法在桥面粗糙状态下得到桥梁一阶振型进而识别了损伤。

基于车辆响应识别桥梁损伤，不需要现场安装测试仪器、随测随走，具有高效、操作方便、节约成本等优点，也不需要进行海量数据的处理，可以随时测量随时处理，能够满足数量越来越多的中小旧桥检测工作，其应用前景巨大。基于车辆响应识别桥梁模态，进而识别桥梁损伤的方法起步较晚，理论研究不够完善，基于此，笔者提出基于位移曲率识别桥梁损伤的三大指标并采用简支梁桥进行数值模拟试验，为推动间接测量法识别桥梁损伤位置提供理论参考。

1 理论依据

公式求解模型为单轴1／4 车辆和简支梁桥。移动量测车质量为mv，刚度为kv，移动速度为v。桥梁总长度为L，单位长度质量为，截面抗弯刚度为EI，桥梁因车辆作用导致振动产生坐标x处挠度为u（x）。

图1 单自由度车辆通过桥梁简图Fig.1 Schematic diagram of single-degree-of-freedom vehicle passing through a bridge

采用有限元方法将桥梁离散化，桥梁振动方程可以表示为：

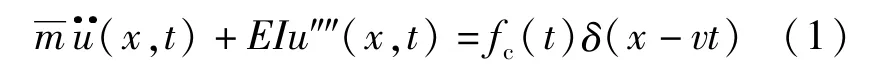
车辆的运动方程可列为：

系列推导可得到要使用的车辆竖向加速度qv（t）的解析解：

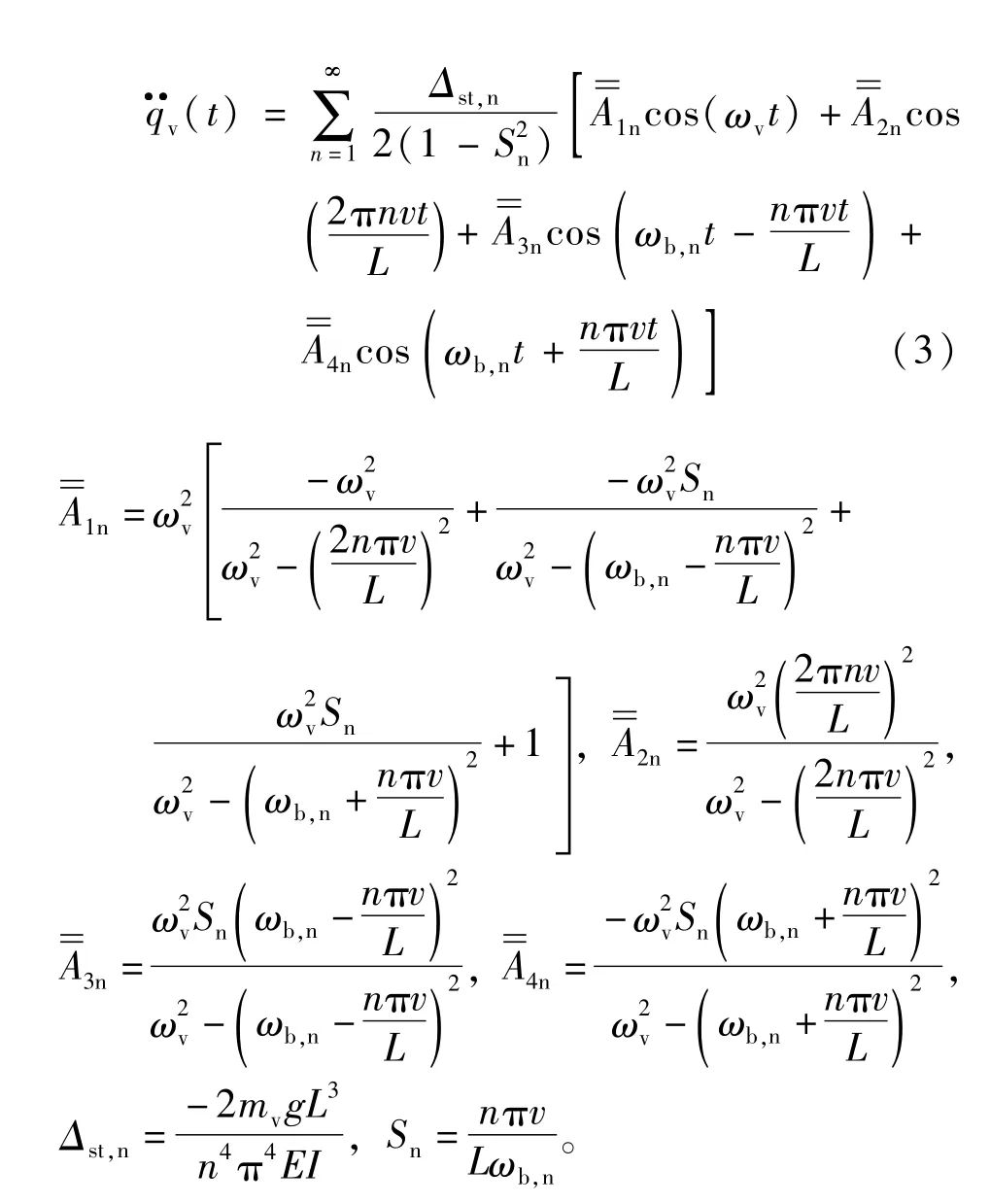
车辆的加速度响应主要由四种类型的频率余弦波所叠加组成，分别为车辆的固有频率ωv，驱车频率2nπv／L，桥梁的左移频率ωb，n－nπv／L 和右移频率ωb，n＋nπv／L。

桥梁振动响应的瞬时振幅解析解为：

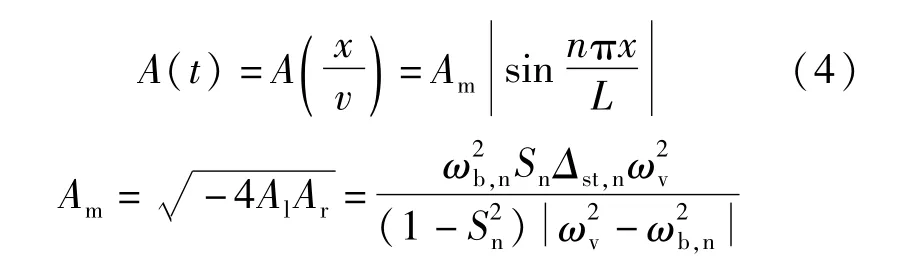
通过式（4）可以看出A（t）为一个常数Am与桥梁的模态函数sinnπx／L 绝对值的乘积，所以A（t）仍是桥梁的模态函数。以此可以得出，只要从车辆竖向振动响应中能够分解出对应于桥梁某阶频率的振动响应，那么我们就得到了相应的瞬时振幅震荡曲线，其曲线的外包络线则代表了桥梁相对应的某阶振型。由于测试车通过了桥上的每一个点，因此可以保证此方法提取振型具有较高的空间分辨率。

2 识别流程与模型参数

2.1 识别流程

（1）使用APDL编制车桥耦合振动计算程序，模拟车辆匀速驶过简支梁桥的过程，提取车体竖向动力加速度时程响应。

（2）对提取出的车体加速度响应进行快速傅里叶变换，得到车体的加速度频谱图，辨识并得到桥梁一阶频率峰值范围。

（3）根据车体频谱图中显示的桥梁一阶频率带范围，对原始的车体竖向动力加速度时程响应进行带通滤波处理，得到一阶桥频分量响应。

（4）对一阶桥频分量响应进行希尔伯特变换，求取一阶桥频分量的瞬时振幅曲线。

（5）对得到的一阶桥频分量响应的瞬时振幅曲线进行重构，得到桥梁第一阶位移振型。

（6）根据得到的桥梁一阶识别位移振型，对其进行单元划分，共划分为30 个单元，求取每个单元的梯形面积积分并绘制相应的面积积分曲线。

（7）根据公式（9）对得到的面积积分曲线求曲率模态振型，确定桥梁损伤单元位置。

（8）利用3 次多项式对损伤桥梁的曲率模态振型曲线拟合，拟合曲线代表桥梁未损伤时的曲率模态振型曲线，对损伤桥梁和未损伤桥梁的曲率矩阵做差，得到曲率差矩阵，绘制曲率模态差曲线后确定桥梁损伤单元位置。

（9）根据公式（11）对损伤桥梁的曲率进行处理，得到损伤桥梁的曲率变化率曲线后确定桥梁损伤单元位置。

2.2 模型参数

基于分离法原理与车辆动力学理论，将车辆模型与桥梁模型分别建模，利用约束方程实现任意时刻车轮和桥面接触点的位移协调关系（相应的力的平衡关系自动满足），通过APDL 编程实现车辆过桥的耦合动力时程响应分析［20，21］。

1.桥梁建模

假设桥梁总长度L ＝30m，单位质量密度ρ ＝1000kg／m，杨氏模量E ＝27.5GPa；移动量测车的质量mv＝1000kg，刚度kv＝170kN／m，移动速度v ＝1m／s，暂不考虑桥梁和车辆阻尼的影响。时间步长取Δt ＝0.005s。有限元中将桥梁划分为6000 个单元，每个单元长度为0.005m。

2.车辆建模

车辆模型采用单轴1／4车辆模型，如图2 所示。

图2 1／4 单自由度车辆模型Fig.2 Articulated vehicle identification spectrum

竖向振动频率计算公式：

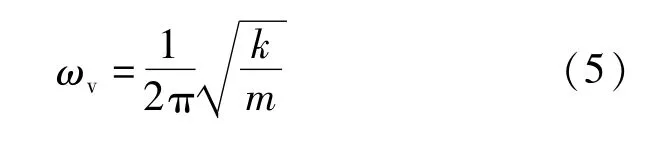
3 位移曲率法损伤识别

首先基于有限元软件的模态分析模块，对距桥梁左端点15m ～16m 部分梁段施加损伤，刚度折减20%，模态分析得到理论位移振型图，对位移振型图进行处理，得到基于位移振型曲率的三大损伤指标曲线图，将得到的损伤指标曲线图作为理论参考，与数值试验得到的损伤指标曲线图进行对比分析。

3.1 频率识别

基于位移振型曲率进行桥梁损伤的识别，必须保证识别出的位移振型有足够高的精确度。车体的加速度时程信息包含了驱车频率对应的时程、车体自振频率对应的时程、桥梁各阶模态对应的时程。采用单轴1／4 车辆，以1m／s 车速匀速驶过简支梁桥，提取车体加速度时程响应，如图3 所示。

从图3 可知，此加速度时程外包络图主要是桥梁一阶模态振动形式的体现，桥梁振动的高能信号主要集中于桥梁低阶，因此这也是选取一阶位移振型进行桥梁损伤识别的原因。

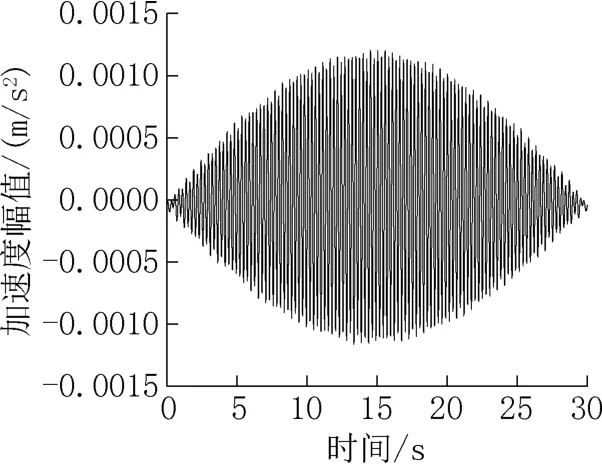
图3 车体加速度时程Fig.3 Time history diagram of vehicle acceleration

在车体加速度频谱图4 可以看出，驱车频率和车体自振频率这两个车辆频率峰值较弱，间距较大，桥梁一阶频率峰值较高，这体现出了桥梁振动信号基本不会受到车辆振动信号的污染，桥梁振动响应在车辆振动响应中有足够的体现，这也是车辆保持低速条件下的优势。

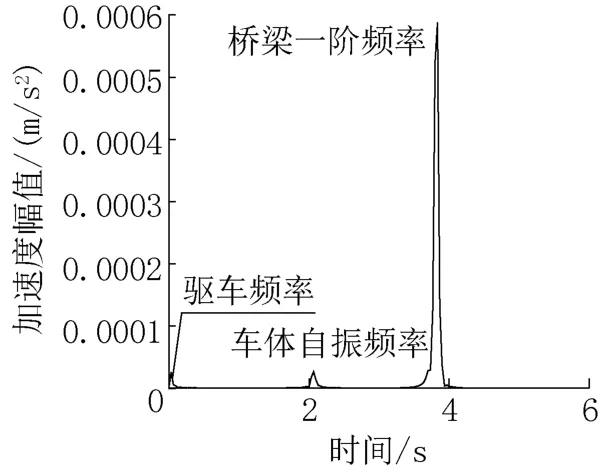
图4 车体加速度频谱Fig.4 Spectrum of vehicle acceleration

3.2 振型识别

通过图5、图6 可以看出，基于车辆传感的方法能够较好的识别出损伤桥梁的位移振型，但是位移振型并不能够体现出桥梁结构的损伤；车辆传感方法识别位移振型有足够高的精度，一阶MAC值能够达到0.99。

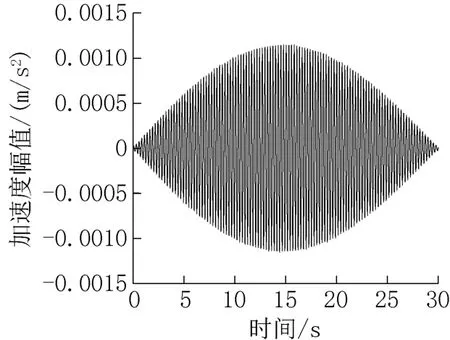
图5 损伤桥梁一阶桥频分量响应Fig.5 First-order frequency component response diagram of damaged bridge

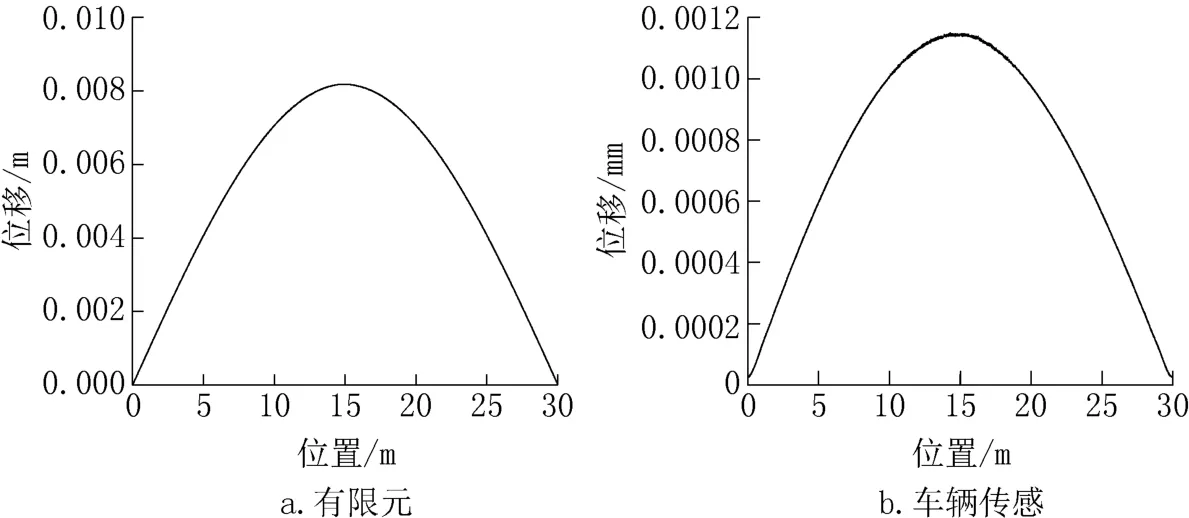
图6 位移振型识别图Fig.6 Recognition diagram of displacement mode

3.3 损伤指标

结构局部特性的变化能够通过曲率模态／应变模态反映出来，曲率模态可通过各阶位移振型计算得到，相对于位移模态对局部结构损伤的敏感性大大提高。曲率模态法的桥梁损伤识别，是现场实测出受损桥梁结构的模态振型，然后用差分法根据实测数据来计算曲率模态，最后由曲率模态振型曲线的突变来确定桥梁的损伤位置。从现有的研究成果来看，结构发生局部损伤，如钢筋锈蚀、裂缝等，导致结构的局部刚度下降，从而导致曲率模态的振型曲线，在损伤位置处发生幅值突变，为曲率模态法的桥梁损伤识别提供分析基础。

曲率的测量有两种方法，一种方法是通过各层面应变和曲率之间的关系，用测量的应变值来换算计算曲率，这种方法可准确的获取中小型结构的曲率。另外一种方法是根据位移振型的测试数据，然后通过差分近似计算位移振型的曲率模态振型。本文采用第二种方法进行曲率的识别。

基于位移振型曲率进行桥梁损伤识别主要有三种方法，分别是曲率模态法、曲率模态差法、曲率模态变化率法。

对于一般梁在受弯曲变形过程中，其中性层的曲率为：

式中：k代表曲率；M代表弯矩；EI 代表梁的弯曲刚度。从式（6）可以看出，梁的某一点的曲率和与对应的弯曲刚度成反比，即结构刚度的变化能够由曲率反映出来。通过模态分析所得到的振型，一般是位移模态，通过位移模态适当变化可以得到曲率模态。

位移模态方程如下：

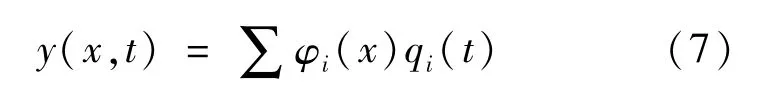
式中：qi（t）、φi（x）分别代表模态坐标和位移振型。

由曲率曲线公式：

将式（7）代入式（8）得到振型曲率φ″i（x），在得到位移模态后，用差分近似计算得到：

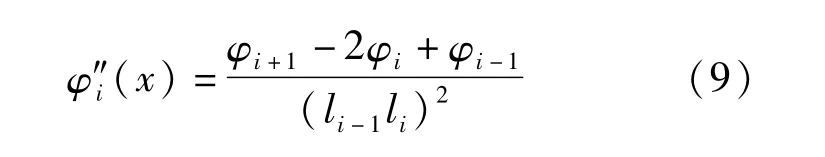
式中：下标i为第i 个测点，li－1li是两个相邻测点i－1 和i之间的距离。

曲率模态法是以受损梁的曲率模态振型为损伤定位参数。当结构存在损伤时，刚度EI 在损伤区域减少，会引起对应曲率的增大，因此，结构中的损伤可以用其改变来实现识别。

曲率模态差法是以在损伤前后梁的曲率模态差作为损伤定位参数。结构在出现破损处，刚度就会降低，曲率模态差增大，而且随着损伤程度的增大，振型曲率的变化增大。所以，通过计算振型曲率差，绘制变化曲线确定损伤位置。表达式如式（10）所示。

式中：φ″0为桥梁未损伤时的振型曲率；φ″s为桥梁损伤时的振型曲率。

曲率模态变化率法能够较好的辨识出桥梁的局部损伤位置和损伤程度：

式中：φ″i＋1为i ＋1 节点的曲率；φ″i为i 节点的曲率。

桥梁梁体局部损伤后，会导致梁体局部刚度下降，位移振型对于局部刚度的下降并不敏感，曲率对于梁体局部损伤具有较高的敏感度，梁体局部特性的改变能够通过曲率模态振型反映出来。由于损伤识别是基于刚度矩阵，因此基于高阶位移振型曲率识别损伤更为精确，但是高阶模态获取较为困难，目前研究较多的仍是桥梁一阶模态。曲率模态振型、曲率模态差及曲率变化率损伤识别的研究结果表明，这三个指标本身抗噪能力很低，实际应用需要对测量数据进行抗噪处理。

以上简要介绍了位移模态曲率法识别桥梁损伤位置的基本原理。对车辆加速度时程进行带通滤波及希尔伯特变换后得到桥梁第一阶的位移模态，据式（8）对桥梁第一阶位移模态进行相关处理，得到曲率；基于曲率，据式（9）～（11）得到识别桥梁损伤的三大指标。

通过图7 看出，基于曲率模态指标的方法能够较好的识别出桥梁损伤的位置。值得注意的是基于车辆传感、利用曲率进行损伤识别时，靠近桥梁端点处的曲率会有异常，所以不能识别靠近桥梁端点位置处的损伤。也可以看出桥梁的损伤区间在识别图中一般体现为峰值左边部分。

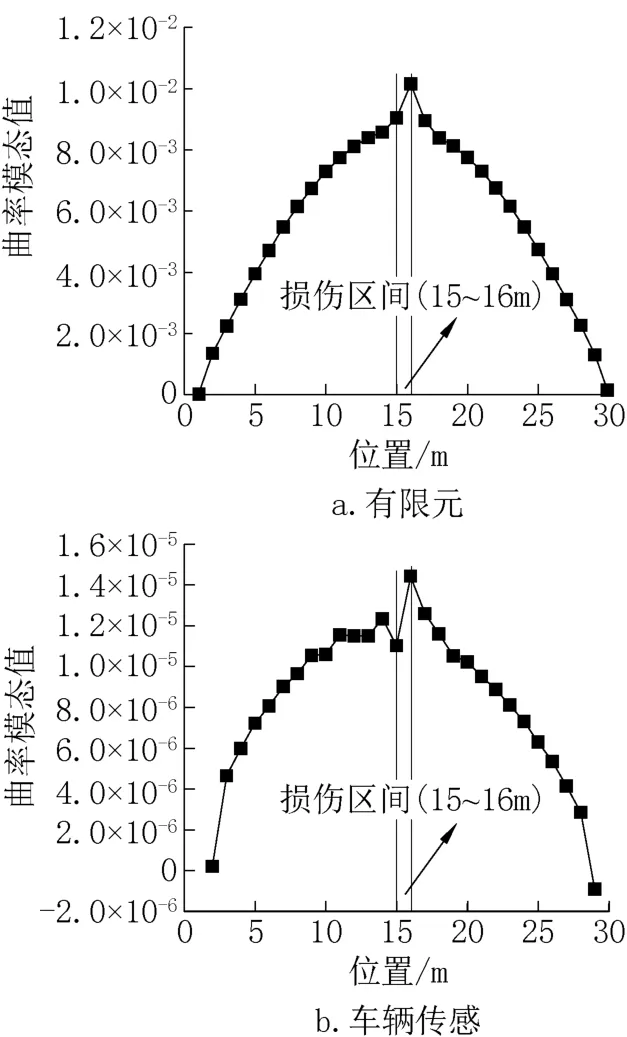
图7 曲率模态识别图Fig.7 Curvature mode shape identification diagram

通过图8 看出，基于曲率模态差指标的方法能够较好的识别出桥梁损伤的位置。由于曲率模态差是对桥梁损伤和未损伤的曲率进行差值处理的方法，因此亦不能识别靠近桥梁端点位置处的损伤。桥梁的损伤区间在识别图中依然体现为峰值左边部分。曲率模态差指标较曲率模态指标对损伤更为敏感。

图8 曲率模态差识别图Fig.8 Recognition diagram of curvature modal difference

通过图9 看出，基于曲率变化率指标的方法也能够较好的识别出桥梁损伤的位置。此指标主要是对曲率再次微分处理，因此不能识别靠近桥梁端点位置处的损伤。桥梁的损伤区间在识别图中依然体现为峰值左边部分。曲率变化率指标较曲率模态和曲率模态差指标具有更好的辨识度。

图9 曲率变化率识别图Fig.9 Curvature change rate identification diagram

4 结语

基于车辆传感得到的位移振型曲率，通过曲率模态振型指标、曲率模态差指标、曲率变化率指标均能较好的识别出桥梁的损伤位置。

基于车辆传感间接测量法识别桥梁损伤具有广阔的应用前景，对广大中小旧桥健康监测具有重大应用价值，笔者对当前较为关注的车辆响应识别桥梁损伤问题进行讨论，提出基于车辆传感识别桥梁损伤位置的三大指标并成功进行了数值模拟试验验证，进一步扩展了间接测量法的应用范围，为桥梁快速检测做前期的理论研究积累。

后续还需现场试验的论证，此桥梁损伤间接识别方法在进行现场试验时影响因素较多，例如桥面不平整度、车流、环境振动、测量噪声等等，因此还需要进一步的理论探讨和现场试验。