全电驱分布式无人车路径跟踪控制仿真研究

刘梦琪， 游雨龙， 周枫林

（1 湖南工业大学 机械工程学院， 湖南 株洲 412007； 2 南京航空航天大学 自动化学院， 南京 211106）

0 引 言

全电驱分布式无人车是当前新能源汽车采用的主要形式。 与集中式驱动的传统车辆相比，全电驱分布式无人车采用全电机驱动技术，减少了复杂的传动机构，也为整车运动控制带来了新的挑战。分布式全电驱无人车的优势主要体现在3 个方面：

（1）电机即是执行器又是信息单元，能为动力学反馈控制系统提供精确的信息，是多执行器协调控制的基础；

（2）分布式无人车取消了差速器、变速器以及传动轴等传动部件，内部空间结构更加紧凑，提升了传动效率，降低了能耗；

（3）全电驱无人车驱动电机和转向电机独立可控，即保证了协调控制的驱动性和稳定性，也提升了整车运动的灵活性，使其具备蟹行、原地转向等多种集中式驱动电动车难以实现的机动灵活运动模式。

全电驱分布式无人车相较传统汽车发生的变化，对车辆的稳定性和行驶安全性有重要影响，整车动力学仿真是汽车底盘研发的重要方法。 文献［5-7］均采用传统汽车动力学软件Carsim 和Matlab／Simulink联合仿真方式，成功建立了四轮独立驱动的分布式电动汽车仿真平台。 文献［8］中应用Cruise 软件和Matlab／Simulink 联合仿真的方式，建立了四轮独立驱动的分布式纯电动车仿真平台，并基于此平台开展了整车控制策略的研究。 文献［9］应用ADAMS 软件，建立了四轮驱动的动力学仿真模型，研究不同的驱动力矩分配方式对车辆稳定性的影响。 文献［10］基于Matlab／Simulink，搭建了各子系统及整车的动力学仿真模型，实现了蟹行、原地转向等运动仿真。 然而，现有平台在应用于全电驱分布式无人车运动仿真时，还存在以下几点不足之处：

（1）传统动力学软件（Carsim 或ADAMS）尚没有全电驱分布式无人车的仿真模块，在现有通过Carsim和Simulink 联合仿真或ADAMS 方式建立的独立驱动电动车仿真平台中，无法实现四轮独立制动／转向仿真，从而难以全面模拟无人车的运动模式；

（2）现有基于MATLAB／Simulink 仿真平台的运动控制算法中，忽略了动力学的影响／采用非参数化的动力学模型，不便于对无人车的上层轨迹规划与跟踪算法的研究；

（3）现有参数化动力学控制模型，仅应用于前轴／后轴转向的轨迹跟踪运动学仿真，而针对全电驱分布式移动底盘，尚缺乏运动学模型研究。

针对上述问题，本文对传统汽车动力学软件Carsim 提供的Simulink 接口进行二次开发。 通过断开Carsim 传统汽车模型的驱动端、转向端以及制动端，从Simulink 驱动电机、转向电机模型中直接读取各轮独立可控的驱动力、制动力等实时参数，实现对全电驱分布式无人车的四轮独立驱动／制动／转向电动车的运动学仿真。 最后，采用全电驱分布式无人车的运动学模型，在此平台上对全电驱分布式无人车的转向及轨迹跟踪进行了运动学仿真，验证了该仿真平台的正确性和稳定性。

1 基于Carsim／Simulink 的分布式无人车仿真平台设计

1.1 全电驱分布式无人车模型架构

分布式无人车动力学模型主要是包含3 部分内容：车身外形尺寸以及惯性参数、车辆驱动转向系统、悬架与轮胎系统。 如图1 所示，本文在Carsim中完成整车外形尺寸、空气动力学、悬架与轮胎系统等参数化模型，同时断开Carsim 中的驱动端、转向端和制动端；在Simulink 中建立驱动电机模型和转向电机模型，通过Carsim 软件中的对外数据接口交换，使Carsim 软件中的车辆模型获得独立的驱动力矩、制动力矩、转向角度的瞬态参数，并在Simulink中建立驾驶员模型、算法控制决策模型，以此实现分布式无人车仿真平台的建立，模型架构如图2 所示。

图1 全电驱分布式无人车动力学模型Fig. 1 Dynamics model of distributed unmanned vehicle with full electric drive

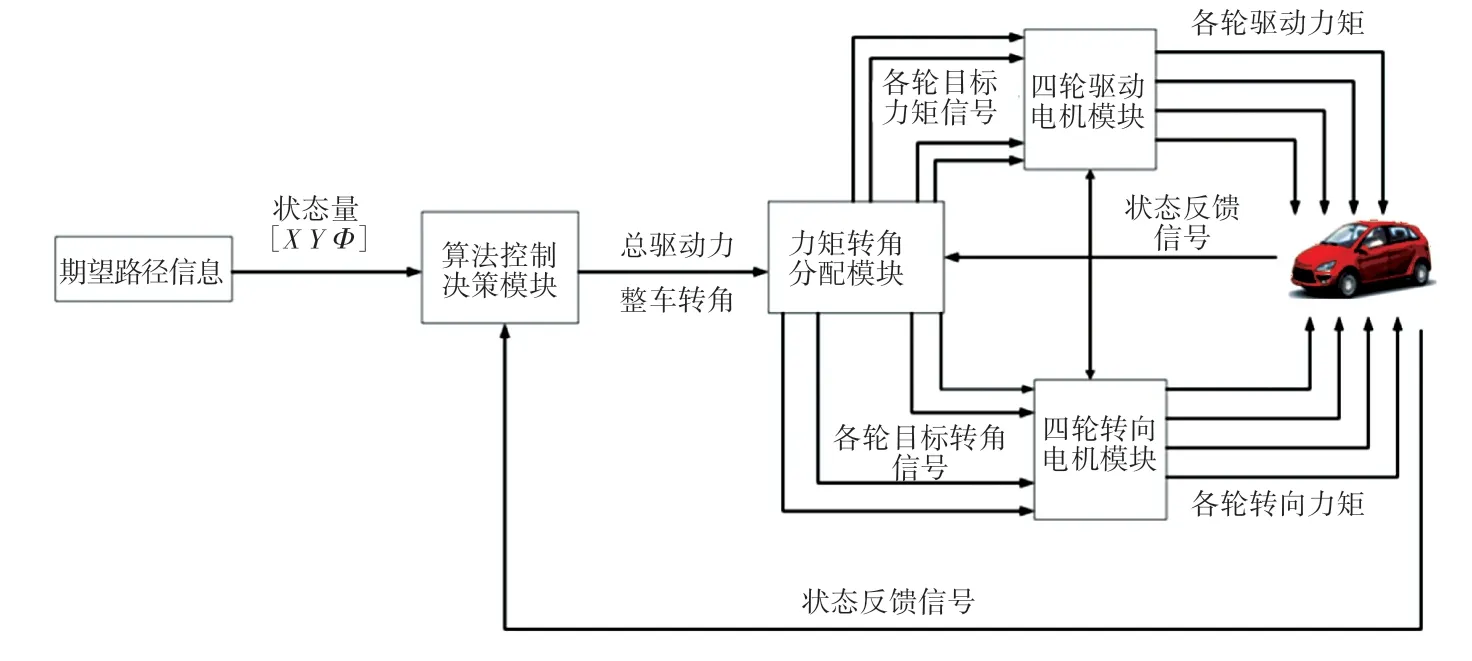
图2 全电驱分布式无人车模型架构Fig. 2 Architecture of distributed unmanned vehicle model with full electric drive

本文选取Carsim 软件中的B-Class 系列轿车模型为分布式无人车仿真平台模型基础，主要对其进行四轮独立驱动／制动／转向等功能的二次开发建模。

1.2 永磁同步电机模型

1.2.1 永磁同步电机驱动

全驱动分布式无人车的驱动电机，采用交流永磁同步电机，其数学模型包括：电压方程、磁链方程、转矩方程与运动方程，电机技术参数详见表1。

表1 交流永磁同步电动机技术参数Tab. 1 Technical parameters of AC permanent magnet synchronous motor

（1）定子电压方程为：

式中，［（，）］ 是定子绕组电流产生的磁场匝链到定子绕组自身的磁链分量，［（，）］ 是转子永磁体磁场匝链到定子绕组的磁链。

（3）电磁转矩方程：根据能量法可知，电磁转矩等于电流不变，是磁能储能对机械角位移的偏导数，交流永磁电动机的电磁转矩［（，）］ 可以表示为：

式中，[] 为自感和互感电动势；n为永磁电动机的极对数；为电气角位移。

（4）电动机运动方程： 根据牛顿第二定律可知，电机运动方程式为：

式中，为整个机械负载系统折算到电动机轴端的转动惯量，为折算到电动机轴端的负载转矩。

永磁同步电机采用FOC 闭环控制，FOC 主要是通过对电机电流控制，实现对电机转矩（电流）、速度、位置的控制。 通常电流作为最内环，速度环是中间环，位置环作为最外环。 当永磁同步电机作为驱动电机进行控制，采用电流和速度的双闭环控制，控制系统流程如图3 所示。 当永磁同步电机作为转向电机进行控制，采用位置、速度和电流的三闭环控制，控制系统流程如图4 所示。

1.2.2 永磁同步电机转矩响应特性分析

根据电机控制系统流程，建立Simulink 电机控制系统仿真模型（如图5），对其进行仿真测试。 永磁同步电机Simulink 模型转矩响应曲线如图6 所示，目标转矩为50 N∗m，实际电机反馈转矩响应时间为3 ms 左右，因此所建立的电机模型具有良好的转矩响应特性，符合实际电机响应情况。

图3 速度电流双环控制流程Fig. 3 Flow chart of speed current double-loop control

图4 位置速度电流三环控制流程Fig. 4 Flow chart of position， velocity and current three-loop control

图5 永磁同步电机Simulink 仿真模型Fig. 5 Simulink simulation model of permanent magnet synchronous motor

图6 电机转矩跟踪响应图Fig. 6 Motor torque tracking response diagram

目前，国内转向电机大多采用有刷直流电机，虽然控制方法简单，但系统运行效率低，在汽车领域内受到限制。 永磁同步电机具有功率密度大、效率高等特性。 因此，本文同样将永磁同步电机作为转向电机，其建模过程同驱动电机相同。

2 四轮阿克曼模型转向运动仿真方法

2.1 转向模式

全电驱分布式无人车由于具备四轮独立驱动独立转向系统，使其拥有两轮转向、四轮转向、四轮差速转向、中心转向、蟹行、中心差速转向和纯差速转向模式，具体功能描述见表2 所示。 6 种转向运动学模型如图7 所示。

表2 6 种转向模式Tab. 2 Six steering modes

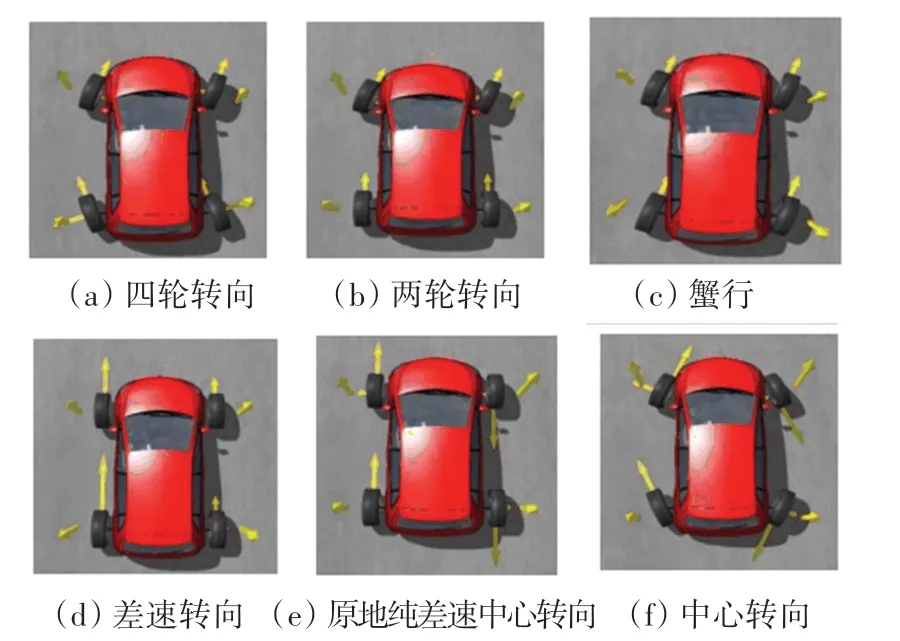
图7 无人车6 种转向运动的实现Fig. 7 Realization of six steering directions of movements of unmanned vehicle

在基于Carsim／Simulink 的全电驱分布式无人车仿真平台上，通过轮速和转角控制，可以实现以上6 种转向功能模式。

2.2 四轮阿克曼转向运动学分析

为了简化模型，需进行如下假设：

（1）忽略汽车车轮的定位参数，即不考虑主销内倾角、主销后倾角、车轮外倾角、前束对汽车转向运动的影响；

（2）假设车轮为刚性车轮，忽略轮胎弹性侧偏等影响；

（3）忽略机构杆件之间的空间夹角和间隙，建立转向机构的平面数学模型；

（4）规定汽车左转时，左、右转向轮的转角为正；右转时，转角为负。

2.2.1 传统两轮阿克曼理论车辆转向模型

阿克曼转向原理主要解决车辆转向运动过程中车轮磨损过快的问题。 其主要方式为：车辆的内侧和外侧车轮在转向时必须绕一个瞬时中心做圆周运动，从而保证车轮与地面处于纯滚动无滑移现象，以实现车辆顺畅转弯。

阿克曼原理的基本观点是汽车在行驶过程中，每个车轮的运动轨迹必须符合其自然运动轨迹。 传统车辆通过连杆结构，转向时使内侧轮的转向角度大于外侧轮的转向角度，并使4 个车轮的旋转中心位于后轴延长线上，车轮中心与车辆旋转中心的连线与车轮速度方向成90°。 基于阿克曼原理的无人车右转运动学模型如图8 所示。

图8 中，为左右两侧轮距；为前后轴轴距；、分别为前后轴到质心的距离；为后轴中心到旋转中心的距离；R为质心到旋转转向的距离，即车辆的旋转半径、、、分别为各个车轮绕旋转中心的转向半径；、、、分别为各个车轮的纵向速度；为质心速度；和分别为前两轮的转向角度；为前轴中点处的转角。 本文将定义为整车模型前轴的瞬时转角，R为整车模型的转向半径。

图8 传统两轮阿克曼转向运动学模型Fig. 8 Traditional two-wheel Ackermann steering kinematics model

由几何关系可得：

2.2.2 四轮阿克曼转向运动学模型

传统两轮阿克曼转向是一种较为理想的状态，传统汽车通过机械连接实现这种转向方式，会造成控制转角精度差，高速时转向半径偏大，车轮磨损严重，甚至在恶劣工况下，转向机构无法完成阿克曼转向角。 基于此问题，本文在传统阿克曼转向理论上进行优化设计，针对全电驱分布式无人车独立驱动、独立转向的优势，进行四轮阿克曼转向运动学分析研究，如图9 所示。

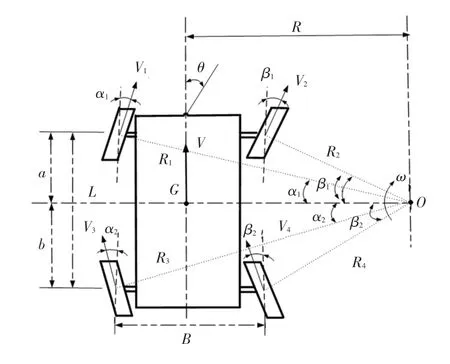
图9 四轮阿克曼转向运动学模型Fig. 9 Four-wheel Ackerman steering kinematics model

图9 为四轮阿克曼转向示意图，为质心到旋转转向的距离；、、、为各个车轮的转向角度；其余变量意义与两轮阿克曼转向定义相同。同样，将定义为整车模型前轴的瞬时转角，R 为整车模型的转向半径。 由图9 中所示几何关系可知：

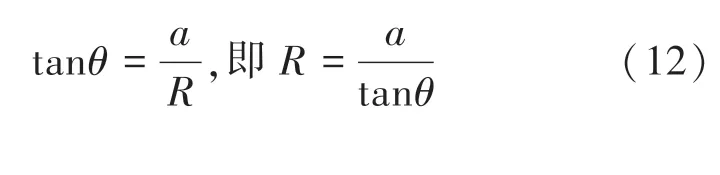
2.3 四轮阿克曼转向运动学仿真验证

2.3.1 车速控制

（1）车速控制策略：车速采用跟踪增量式PID控制方法，控制策略如图10 所示，保证在不同的负载都能保持期望车速；

（2）车速跟踪控制策略验证：在路面附着系数为1.0 的沥青路面进行直驶加速测试，仿真时间10 s，驾驶员期望车速为：

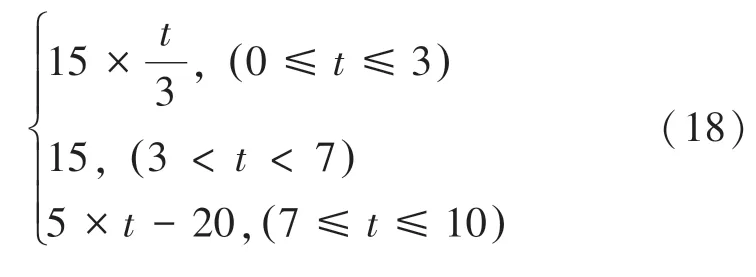
图10 增量式PID 车速控制流程Fig. 10 Incremental PID speed control flow chart

仿真数据如图11 所示。 在跟踪变速度测试时，由同一时刻的、两点可知，车辆实际速度与驾驶员期望速度差值为1 km／h，并在随后的点（0.2 s后），实际车速能跟踪上期望速度。 在跟踪恒定速度测试时，由、两点数据可知，再经过0.2 s 后，实际车速能跟踪上期望速度，并且能够保持很小的速度误差，如图12 所示。

图11 车速跟踪图Fig. 11 Speed tracking chart

2.3.2 四轮阿克曼转向运动学仿真验证

基于Carsim／Simulink 的全电驱分布式无人车仿真平台上的转向测试，特设定以下控制量：

前轴中心转角25°，时速35 km／h，行驶30 s，控制周期0.001 s。 由两轮阿克曼转向模型和四轮阿克曼转向模型计算出表3 所示的理论控制量。

图12 车速跟踪误差图Fig. 12 Speed tracking error diagram

表3 两种转向模式的理论控制量Tab. 3 Theoretical control quantities for two steering modes

经过仿真测试，两种转向运动性能如图13 ～图18 所示。

仿真数据表明，在同一工况和驾驶员指令下得到如下结果：

（1）两轮与四轮阿克曼转向直径分别为15.6 m和9.8 m。 即两轮阿克曼转向模式的转向半径大于四轮阿克曼转向模式的转向半径，且超过近0.6 倍（如图13～14 所示）；

图13 两轮阿克曼转向运动轨迹Fig. 13 Two Ackermann steering trajectories

图14 四轮阿克曼转向运动轨迹Fig. 14 Steering trajectory of four Ackermann wheels

（2）两轮阿克曼转向模式的应用中，由于前轮转向角度较大且左、右前轮转角差较大，需要克服侧向力也更大，左前轮与地面受到摩擦阻力大，大于轮胎与地面的静摩擦力，使得前左轮速度出现上下波动（如图15 所示）。 同时，该模式也造成前左轮电机输出力矩剧烈震荡（如图17 所示），对电机的健康运行有较大负面影响；

（3）四轮阿克曼转向在实现期望车速与期望转角转向时，左前轮转角小，且左、右前轮转角差也较小，四轮都进行转动并提供转向摩擦力。 因此，单个车轮需要的转向摩擦力更小，能够实现平稳控制。该模式下，车辆能实现更小的转向半径，且能保持轮速和电机力矩稳定，有助于电机运行安全和无人车的安全行驶（如图16、图18 所示）。

图15 两轮阿克曼转向速度跟踪Fig. 15 Two rounds of Ackermann steering speed tracking

图16 四轮阿克曼转向速度跟踪Fig. 16 Four rounds of Ackermann steering speed tracking

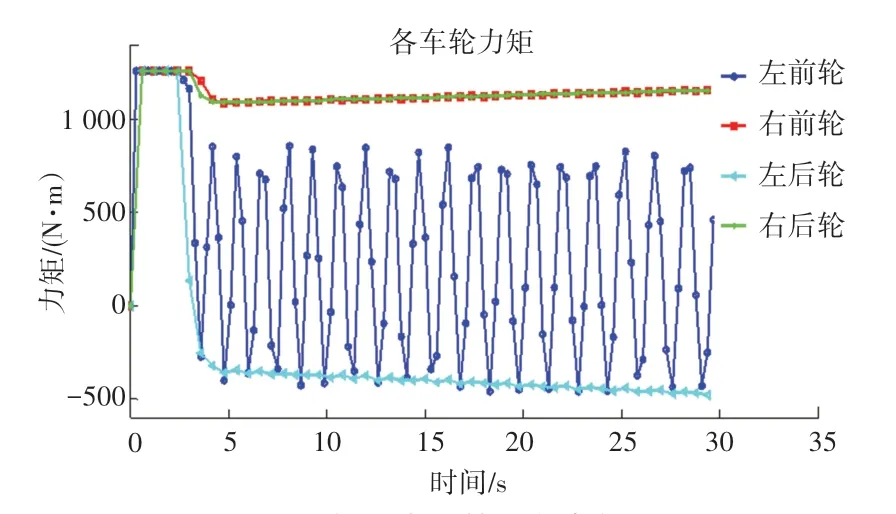
图17 两轮阿克曼转向各车轮力矩Fig. 17 Torque of two Ackermann steering wheels

图18 四轮阿克曼转向各车轮力矩Fig. 18 Torque of four Ackermann steering wheels

因此，本文将四轮阿克曼转向作为全电驱分布式无人车的常用转向模式。

3 基于分层运动学模型的路径跟踪运动控制仿真

3.1 全电驱分布式无人车路径跟踪运动学模型

由于全电驱分布式无人车独立驱动／转向的优势，其路径跟踪运动学模型设计为上下两层，如图19 所示。 上层运动学模型不考虑无人车的四轮独立转向独立驱动的功能，将无人车视作为一个整体，分析其质心速度和前轴中心转角。 下层运动学模型基于四轮阿克曼转向理论模型，将质心速度和前轴中心偏角映射到各自的四轮速度和四轮转角，实现对分布式无人车的路径跟踪控制。

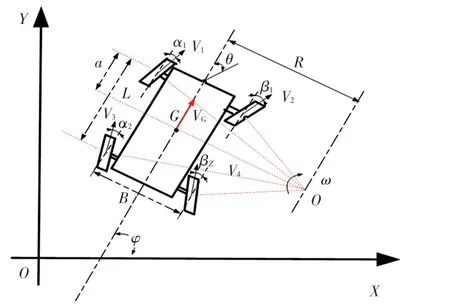
图19 分布式无人车路径跟踪运动学模型Fig. 19 Kinematics model of distributed unmanned vehicle path tracking

3.1.1 上层运动学分析

由于在分布式无人车路径跟踪控制过程中，以、作为控制量，所以该模型可被进一步表示为：

式中，状态量·，，]，控制量［，］。

3.1.2 下层运动学分析

由上层运动学可知，在整车路径跟踪控制过程中，速度和前轴转角关于状态量［X，Y，］ 的关系。 下层运动学利用四轮阿克曼转向模型，将车质心速度和前轴转角映射到四轮速度［、、、］ 和转角［，，，］ 控制量，实现对期望路径的跟踪控制。

3.2 全电驱分布式无人车运动学模型验证

为了验证全电驱分布式无人车运动学路径跟踪模型，在Matlab 环境中用m 语言建立该运动学模型，并在相同输入条件下，与基于Carsim／Simulink所建立的分布式无人车平台的整车模型进行对比。其中，相同的输入条件是指前轴转向角与车速随时间的变化历程相同，输出均为分布式无人车的位置和航向状态量。

设定：无人车初始状态＝ 0，0，0[ ] ，无人车速度17 km／h，无人车前轴转向角45∗sin（），仿真时间10 s，运行周期0.001 s。

由分布式驱动无人车下层运动学，可计算出4 个车轮的转向角与速度控制量，如图20～23 所示。

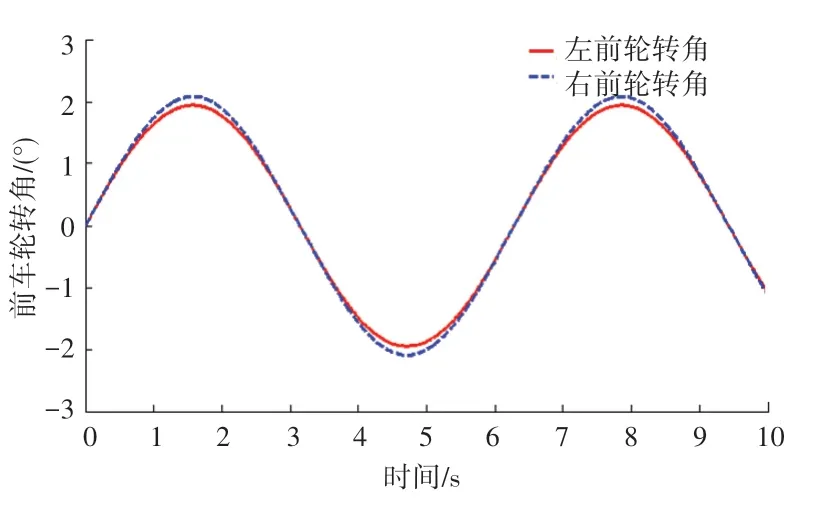
图20 前轮转角信号变化图Fig. 20 Changes of front wheel Angle signal

图21 后轮转角信号变化图Fig. 21 signal changes of rear wheel Angle

图22 前轮车速信号变化图Fig. 22 Changes of front wheel speed signal

图23 后轮速度信号变化图Fig. 23 Speed signal change diagram of rear wheel

m 语言模型和Carsim／Simulink 模式数据对比如图24～26 所示。

图24 路径跟踪对比图Fig. 24 Path tracking comparison diagram

图25 航向角对比Fig. 25 Course Angle comparison

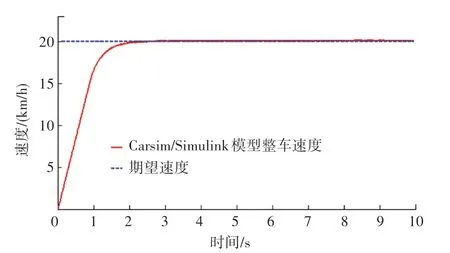
图26 车速随时间变化历程Fig. 26 Change of vehicle speed with time

4 结束语

本文确定了全电驱分布式驱动无人车整车模型架构，利用MATLAB／Simulink 软件建立了驱动以及转向电机模型，结合增量式PID 控制算法，建立了无人车的独立驱动／转向／制动系统以及车速跟踪模型，从而完成了基于Carsim／Simulink 的全电驱分布式无人车仿真平台的建立。 此外，基于传统两轮阿克曼转向原理，针对分布式无人车独立驱动、独立转向的功能优势，进行四轮阿克曼转向运动学设计，使全电驱分布式驱动无人车四轮阿克曼转向实现了更小的转向半径，且能较好的保持速度稳定和力学响应特性。 最后，基于全电驱分布式无人车独立驱动／转向的优势，将路径跟踪运动学模型设计为上下两层，上层运动学可知在整车路径跟踪控制过程中的速度和前轴转角状态量的关系，下层运动学利用四轮阿克曼转向模型，将车质心速度和前轴转角映射到四轮速度和转角控制量。 经仿真验证，基于分布式无人车的分层运动学理论能够较好的反映车辆行驶时的运动特性，为后续轨迹跟踪控制算法提供了有效的仿真平台与理论基础。