风险偏好影响下的创新产品扩散研究

潘明露， 代牧遥

（上海理工大学 管理学院， 上海 200093）

0 引 言

随着信息化、全球化、智能化的到来，科技创新的优势越来越突出，越来越多的创新产品涌入市场，产品扩散过程变得越来越复杂。 同时，由于消费者之间的交流变得更加频繁和方便，个体消费者的采纳决策越来越受到社交网络中其他消费者的影响。 然而，产品只有在社交网络中进行有效扩散才能实现其社会价值和经济价值，这就意味着研究现实生活中创新产品的扩散机制至关重要。

在现实世界中，创新产品总是伴随着质量和功能方面的风险。 不同的消费者对待风险有不同的态度，其态度与个人的经验和自身性格有关，可以分为风险规避和风险偏好。 事实上，风险偏好决定了消费者决策和个人对市场条件的反应，是影响创新产品扩散的关键因素。 例如，规避风险的人不太愿意采用自动驾驶汽车。 此外，消费者所处的社交网络特性一般不是同质或不相关的。 比如，人们往往与相同地位的人交往，从而形成熟人社交网络，该网络实际上具有同配性。 而互联网的发展打破了社会阶层之间的壁垒，使得普通人和名人之间容易建立虚拟的关系，形成在线社交网络，该网络属于异配网络。 因此，本文考虑消费者的风险偏好以及网络的同配性（异配性）特性，仿真分析创新产品的扩散情况。

1 研究现状

针对创新产品扩散的问题，学术界已取得丰硕的研究成果。 其中，最为经典的研究是1969 年Bass提出的Bass 扩散模型。 在Bass 模型中，产品扩散主要受到大众媒体和口碑的影响。 此后近40 年，众多学者为了扩展该模型的应用范围，放宽了其诸多假设，提出了一系列变体。 这些传统模型从宏观角度刻画创新产品扩散过程，为进一步研究产品扩散奠定了丰富的理论基础。

在现实生活中，个体的采纳行为（决定是否购买产品）与其在社交网络中与他人的互动密切相关。 在经典的扩散模型中，假设消费者可以与社交网络中的每个人交流，这与真实世界中的消费者交互情况不相符合。 复杂网络的发展为更接近于现实世界的产品扩散研究提供了理论基础。 从复杂网络的角度来看，个体的采纳决策受其邻居的影响，而不受网络中每个人的影响。 许多学者利用复杂网络来模拟社交网络，用来研究不同网络结构对产品扩散的影响。 研究结果表明，网络异质性显著影响着产品扩散。

产品扩散原理在某种程度上与疾病或谣言传播相似。 在疾病或谣言传播模型中，个体经历多种状态，其在社交网络中受到邻居的影响，经历状态转换。 借鉴疾病或谣言传播的研究思路，许多产品扩散模型被提出。 例如，Fibich 结合Bass 和SIR，提出了Bass-SIR 模型。 在此模型中，个体经历了3种状态：潜在采用者（未购买产品的消费者）、采用者（已购买产品的消费者）和退出采用者（已从采用者状态“恢复”并停止影响他人采用产品的消费者）。 该研究利用Bass-SIR 模型，探索了新产品在不同网络中的扩散，并得出结论：产品扩散只依赖于社会网络的局部结构，而不依赖于消费者之间的平均距离。

消费者的采纳行为不仅受到他人的影响，还会受到自身情感、经验和期望的影响。 因此，消费者自身因素也会影响产品扩散。 Huo 等人构建考虑个体风险偏好的双产品信息扩散模型，采用平均场方法来研究扩散，推导出了扩散的临界阈值，最后利用蒙特卡罗模拟验证了理论分析。 Hong 等人考虑消费者的环保意识，采用Bass 模型考察绿色产品扩散，发现环保意识显著影响着绿色产品扩散。

然而，考虑消费者风险偏好的创新产品扩散研究还很少，且大多数研究局限于使用同质网络或不相关无标度网络模拟社交网络，很少有研究考虑到社交网络中同配性（异配性）混合的特征。 同配性混合指高度顶点优先依附于其他高度顶点，而异配性混合则表现为高度顶点依附于低度顶点。 因此，本文在Bass 模型的基础上考虑消费者的风险偏好，构建创新产品扩散模型，并利用复杂网络模拟社会网络，从网络同配性角度研究网络拓扑结构对创新产品扩散的影响。

2 创新产品扩散模型描述

Bass 模型是创新产品扩散领域研究最多的模型之一，可以表示为：

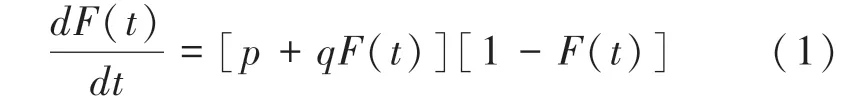
式中，（） 是时刻的采纳者人口密度，、分别为创新系数和模仿系数。

本文将Bass 模型与复杂网络相结合，探讨了创新产品在现实生活中的扩散机制。 在Bass 模型中，消费者有两种不同的状态：潜在采纳状态和采纳状态。 当社交网络中的潜在采纳者从新闻报道等外部正规媒体渠道接收到有关创新产品的信息时，其会以的概率变成采用者。 同时，潜在采用者的状态也会受到社交网络中内部交互的影响。 当潜在采纳者与采纳者接触时，会受到采纳者对产品描述的影响，并以概率变成采纳者。

在本文提出的模型中，引入风险态度系数，来表征不同消费者个体对风险的态度。 消费者可能以概率成为风险偏好者或以概率1成为风险规避者。 因此，在社交网络中消费者有4 种不同的状态：冒险潜在采纳者状态（L）、保守潜在采纳者状态（L）、冒险采纳者状态（F） 和保守采纳者状态（F）。 其中上标和分别表示风险偏好和风险规避状态。 创新产品在消费者群体中的扩散过程如图1 所示。

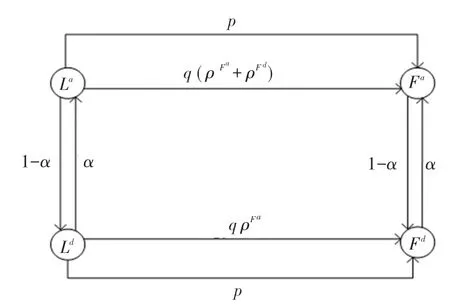
图1 创新产品的扩散过程Fig. 1 The diffusion process of an innovative product

创新产品扩散过程可以表示为：

（1）受消费者风险偏好的影响，发生状态转换时：

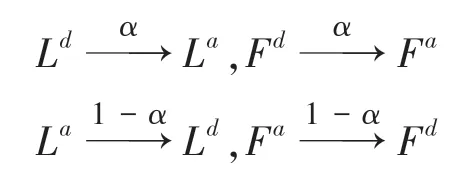
（2）受到创新系数影响，发生状态转换时：

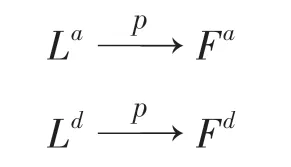
（3）受到模仿系数影响，发生状态转换时：

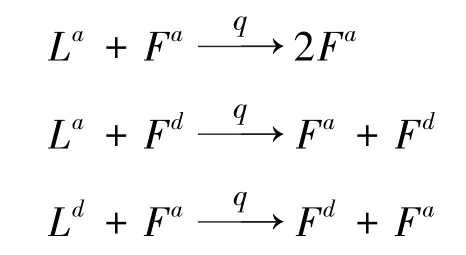
整个扩散过程呈现了复杂网络中潜在采纳节点和采纳节点的状态转换情况。 一个冒险潜在采纳节点与其所有采纳邻点交互，并在与采纳邻点（无论其是冒险或保守）交互时，以概率成为一个冒险采纳节点。 然而，一个保守潜在采纳节点只能与其冒险采纳邻点交互，并以成为保守采纳节点。 此外，冒险潜在采纳节点和保守潜在采纳节点都会受到大众媒体的影响，以概率变为采纳节点。 通过将传统的Bass 模型应用于复杂网络，并将态度系数引入到潜在采纳者和采纳者中，从而实现了更接近于现实社会中的创新产品扩散场景的描述。

3 理论分析

3.1 平均场方程分析

在复杂网络中，每个节点代表一个消费者个体，每条连边表示不同个体之间存在的交互关系，个体在某一时刻所处的状态属于上述4 种状态中的一种。 为了进行平均场分析，按照扩散动力学研究的经典方法，将所有节点按其度划分为不同的类别。（） 表示度类中的节点总数；（，）、（，） 分别表示在时刻，度类中处于潜在采纳状态与采纳状态的节点数目；ρ（，）、ρ（，） 为其对应的密度。 则有：

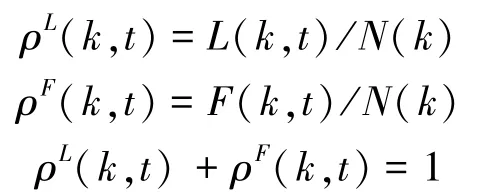
在该模型的假设中，不论消费者持有怎样的风险态度，都会以概率受到大众媒体的影响；并在Δ时间内，由社交网络中的内部交互而发生的消费者状态转移，与大众媒体的影响无关。 因此，首先分析在不考虑创新系数的情况下的状态转换。 在时刻、度类里，任意一个潜在采纳节点将以一个态度系数变成一个冒险潜在采纳者，以1变成一个保守潜在采纳者。 此外，考虑到模仿系数，节点在［，］ 时间段内，状态转移将遵循以下两种情况：

（1）在冒险潜在采纳状态下，节点可以以概率被任意一个采纳邻居节点影响。 假设在时刻有（≤） 个采纳邻居，则在时间后，保持在潜在采纳状态的概率是（1）。有个采纳邻居的概率为：

（2）在保守潜在采纳状态，节点可以以概率被任意一个冒险采纳邻点影响。（≤） 表示为的冒险采纳邻点的个数。 则有个冒险采纳节点的概率为：

通过使用式（8）的转移概率和考虑创新系数，即可推导出时刻，度类里潜在采纳节点的数目为：

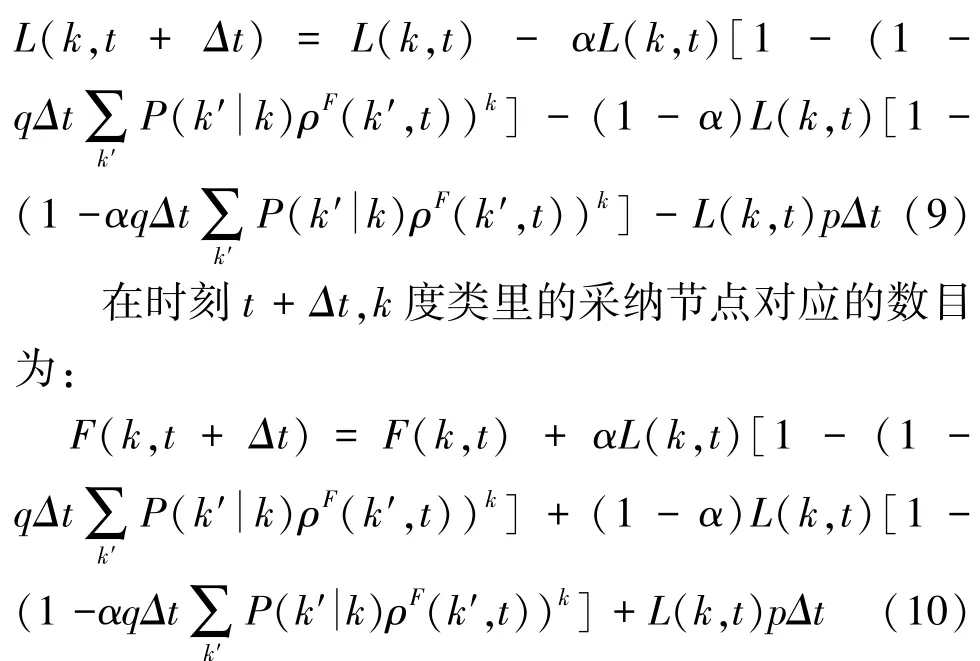
当→0 时，复杂网络中的创新产品扩散对应的平均场方程为：

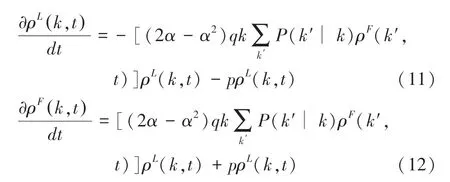
3.2 网络拓扑结构分析

由于创新产品扩散底层网络的信息，通过度度关联函数的形式被嵌入在上述方程中。 因此，需要给出不同网络（） 的表达式。 一些研究表明，社交网络具有异质性，并且展示出同配混合性和异配混合性。 为了研究这些网络特性对提出的模型的动力学的影响，本文考虑了同配无标度网络、异配无标度网络和不相关无标度网络结构。 这些网络的（） 和量化同配等级的Newman 同配系数定义如下：

（1）不相关无标度网络。 在不相关无标度网络中，（） 不依赖，其在文献［15］中被定义为：

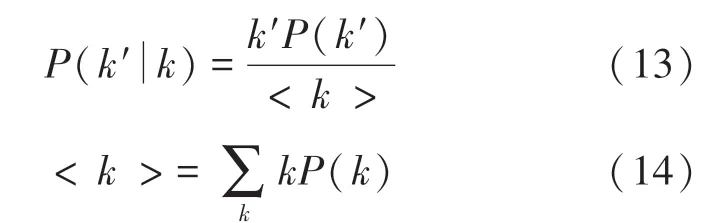
其中，（） 是网络的度关联函数，是平均度。

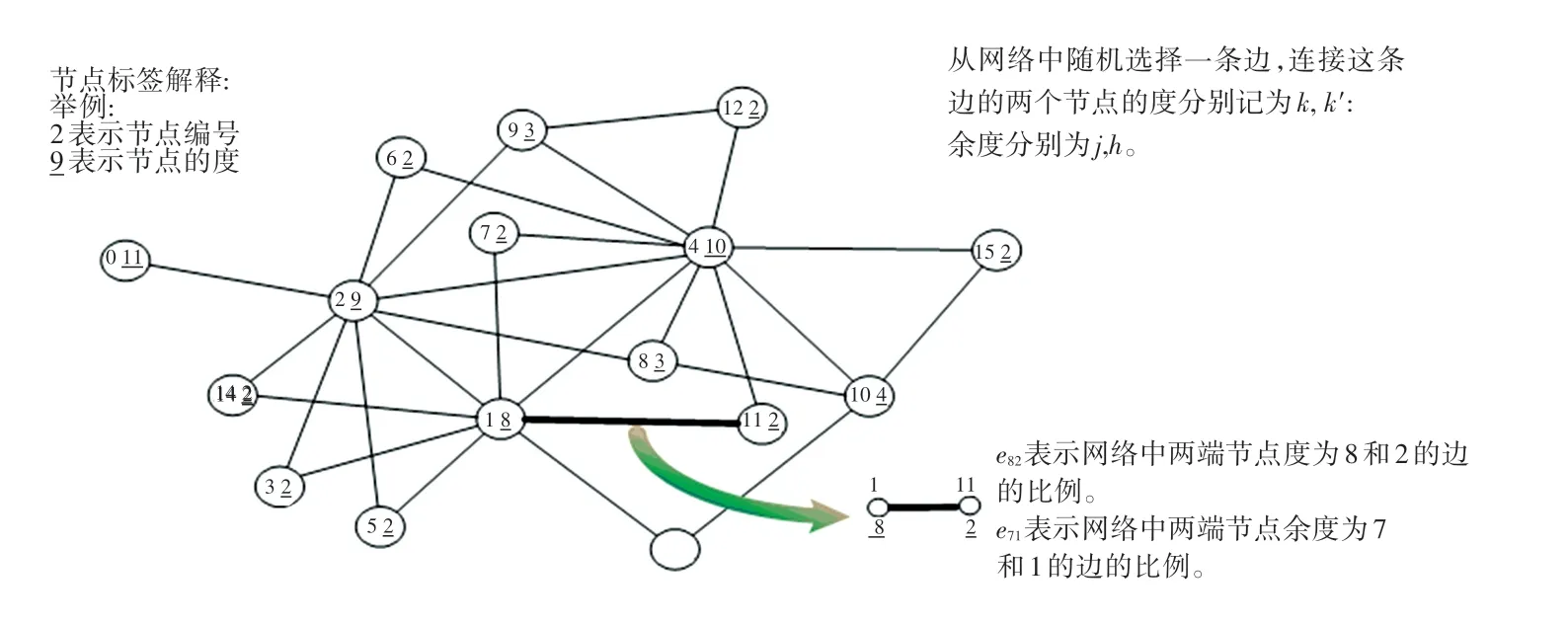
图2 无向相关无标度网络中度度联合概率分布描述Fig. 2 Description of moderate degree joint probability distribution in undirected correlation scale-free network

下面本文根据文献［4］，介绍Newman 同配系数的定义。

一个节点的余度是指其总度减1，节点的余度的标准化分布q为：

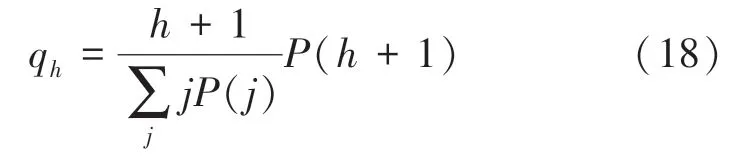
式中，、分别表示随机选择一条边的两端节点余度。 余度分布q的方差是：

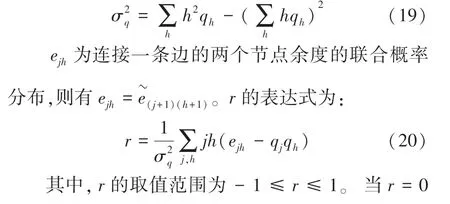
4 仿真实验

基于上述理论分析的数值模拟被实施，来探究消费者的风险偏好，以及网络拓扑结构对创新产品扩散的影响。 从平均场方程分析中可以看到，式（11）、式（12）是由式（9）、式（10）推导而来。 所以，式（9）、式（10）被用作数值模拟的迭代方程。 模拟的初始条件是网络中的所有节点均处于潜在采纳状态，没有采纳节点，即ρ（，0）1、ρ（，0）0。

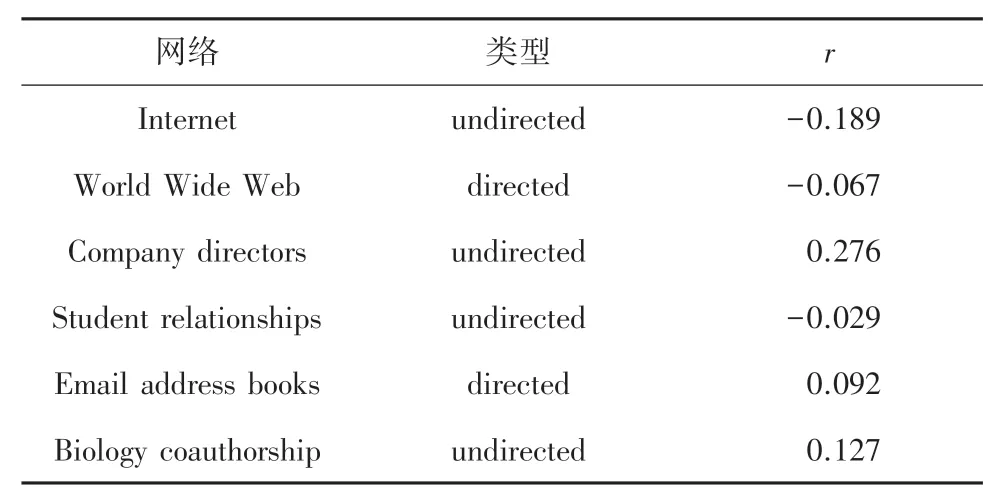
表1 不同网络中的纽曼同配系数r［4］Tab. 1 The Newman assortment coefficientr for different networks［4］

为了得到同配和异配无标度网络，本文使用Xulvi - Brunet 和 Sokolov 算法来重连一个Barabási-Albert（BA）无标度网络，该重连算法可以保留原始网络的度分布。 BA 网络由Python 中的random_graphs.barabasi_albert_graph（n，m）函数生成，此时5 000，2。 参考表1 中真实网络的同配性等级，通过增加重连次数，构建9 个不同同配性的相关无标度网络。 这些网络的同配系数可根据式（15）、式（18）～式（20）计算得出，其分别为：

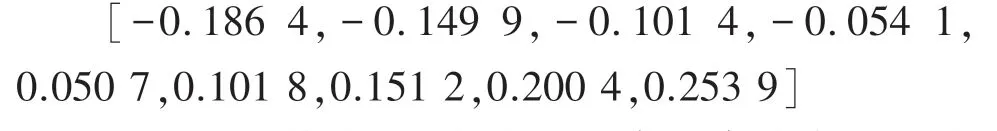
在这些网络中，节点度的联合概率分布基于式（15）得到、网络的度度关联值基于式（16）求得。 此外，不相关无标度网络没有度度关联性，属于中性网络（0）。 其度分布和其余网络相同，其度度相关值可根据式（13）、（14）求解。 在仿真实验中，参照文献［19］，设置0528、0005，且保持固定不变。

4.1 消费者风险偏好对创新产品扩散的影响

图3（a）展示了在几种不同风险度系数下，不相关无标度网络中采纳者比例的时间演化情况。 从中可以看出，无论取何值，创新产品总能扩散到最大规模；但随着的增加，达到最大规模所需的时间逐渐减少。 图3（b）显示了创新产品扩散速度显著依赖于消费者的风险偏好，值越小，产品扩散速率峰值越低，达到扩散速率峰值的时间越长。

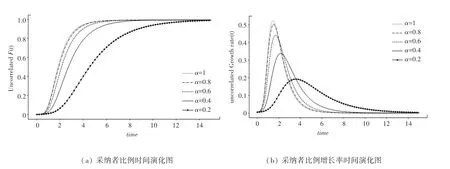
图3 不相关无标度网络中不同α 下的采纳者比例Fig. 3 The proportion of adopters under differentα in uncorrelated scale-free networks

图4（a）、图5（a）分别展示了在不同下，0101 8 的同配无标度网络，以及0101 4 的异配无标度网络下，创新产品采纳者比例的时间演化情况；图4（b）、图5（b）分别描述了扩散速率在相应网络中的时间演化情况。 其他同配性等级网络中的扩散情况如图6、图7 所示。

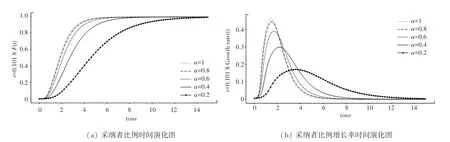
图4 r＝0.101 8 时同配无标度网络中不同α 下的采纳者比例和增长率时间演化图Fig. 4 Time evolution diagram of adopter proportion and growth rate under differentα in co-matching scale-free network whenr＝0.1018

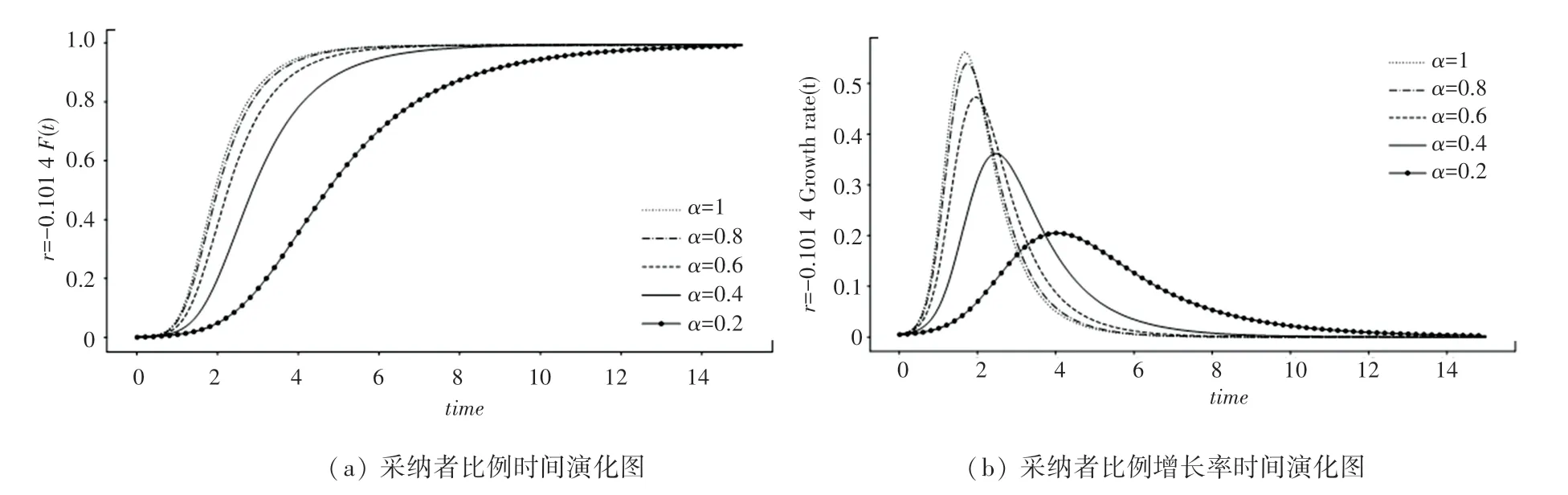
图5 r＝-0.101 4 时异配无标度网络中不同α 的采纳者比例和增长率时间演化图Fig. 5 Time evolution diagram of adopter proportion and growth rate of differentα in heterogeneous scale-free network whenr＝-0.101 4

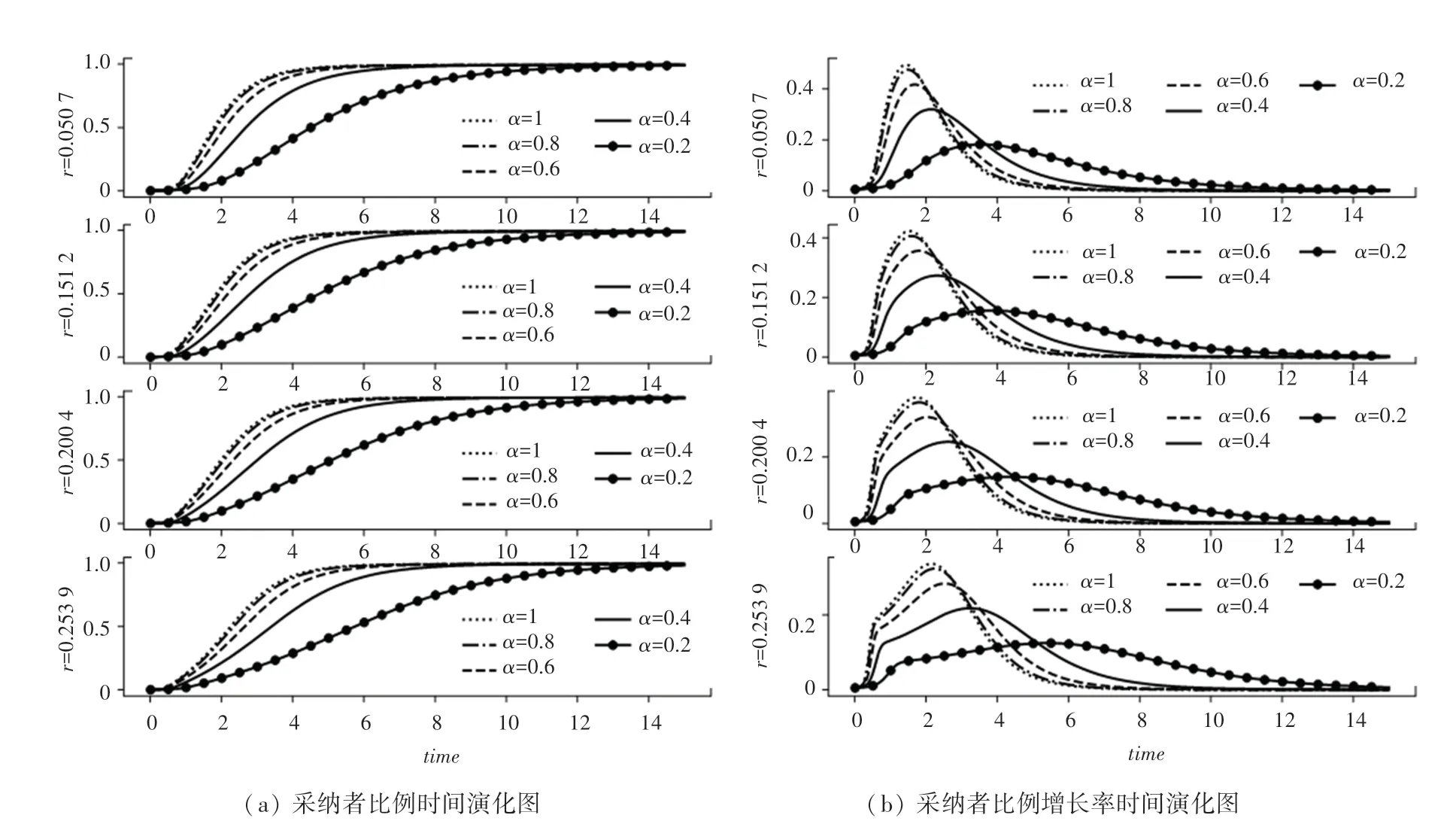
图6 在同配性无标度网络中不同α 的采纳者比例和采纳者比例增长率时间演化图Fig. 6 Time evolution diagram of adopter proportion and adopter proportion growth rate for differentα in assortative scale-free network

图7 在异配性无标度网络中不同α 下的采纳者比例和采纳者比例增长率时间演化图Fig. 7 Time evolution diagram of adopter proportion and adopter proportion growth rate under differentα in heterozygous scale-freenetwork

由仿真结果可知，与不相关无标度网络中的扩散情况相似，创新产品在不同网络中的扩散均随着的增加而加快。 换言之，社交网络中的消费者具有风险偏好态度的可能性越高，消费者之间就越容易相互影响，从而更有利于创新产品的有效扩散。 由此可见，创新产品的扩散在很大程度上取决于消费者的风险偏好。

4.2 网络拓扑结构对创新产品扩散的影响

图8（a）和图8（b）分别展示了02、07时，同配和异配以及不相关无标度网络中，消费者采纳比例时间演化情况的数值模拟结果。 从中可以看出，无论取何值，创新产品在这些网络中均能得到成功扩散。 此外，在0050 7、0102 8 的同配网络中，两种扩散基本重叠；但在另外3 种同配网络中，网络的同配性等级越高，创新产品扩散的越慢。该现象表明，在同配网络中存在一个同配性等级的临界值，使得具有该临界同配性水平的网络结构最有利于产品扩散。 在大于0 小于临界值的情况下，同配性等级的变化对产品扩散没有显著影响；反之，同配性越高的同配网络则越不利于产品的扩散。同时还可以发现，异配网络对产品扩散有类似的影响。 此外， 在同配性（异配性） 系数较小（0050 7、0102 8、0054 1、0101 4）的相关网络中，采纳者比例的时间演化情况与不相关无标度网络（0） 中相似。

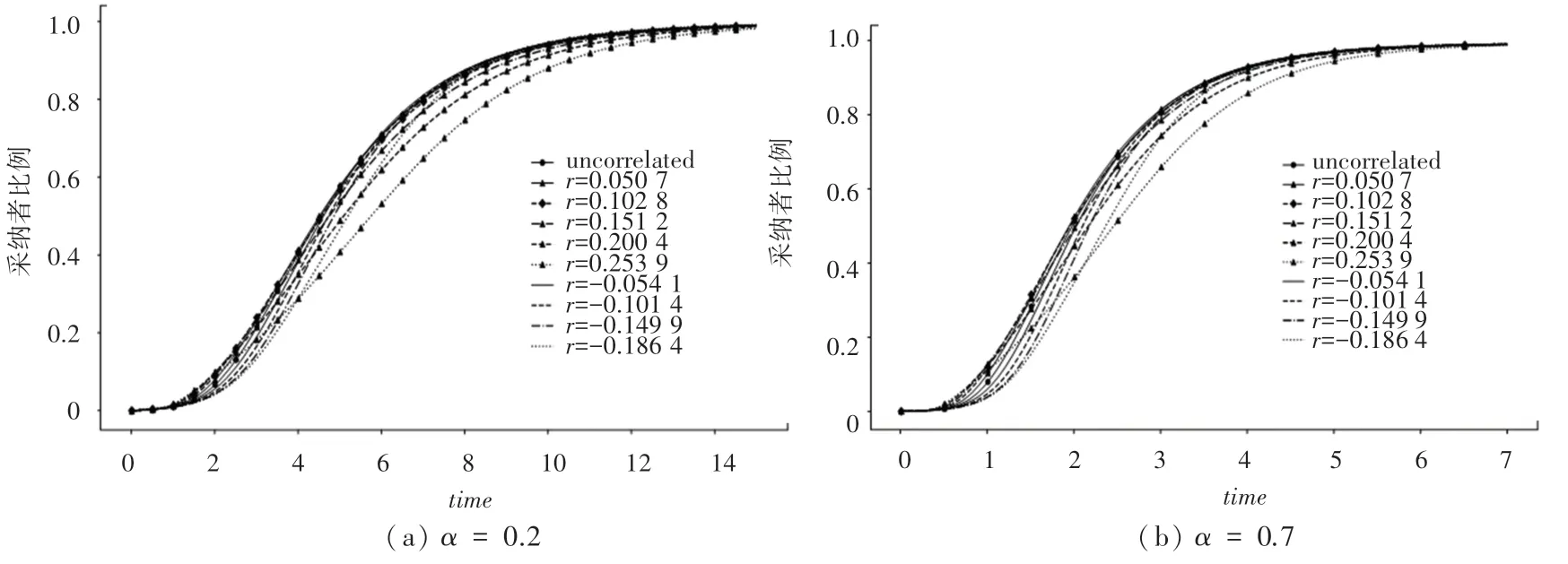
图8 不同网络中α＝0.2 下采纳者比例和α＝0.7 下采纳者比例的时间演化图Fig. 8 Time evolution diagram of the proportion of adopters underα＝0.2 and the proportion of adopters underα＝0.7 in different networks

图9 给出了在值为0.2、0.7 的情况下，同配和异配以及不相关无标度网络中，采纳者比例增长率时间演化的数值模拟结果。 由此可以看出，除0151 2、0200 4、0253 9、0186 4 的网络之外，在其他的网络中，不论取何值，在创新产品扩散早期，同配系数越大，扩散速度越快；但在中期，情况发生了逆转；在后期，不同网络中的扩散速度基本相同。 此外，在异配无标度网络中，增长率峰值是相近的，而在同配无标度网络中呈现出相反的现象。另一方面， 较高的同配性等级或异配性等级（0151 2、0200 4、0253 9、0186 4），导致了较小的扩散速率和较长的扩散时间，并且这样的特性在同配无标度网络中表现更为明显。

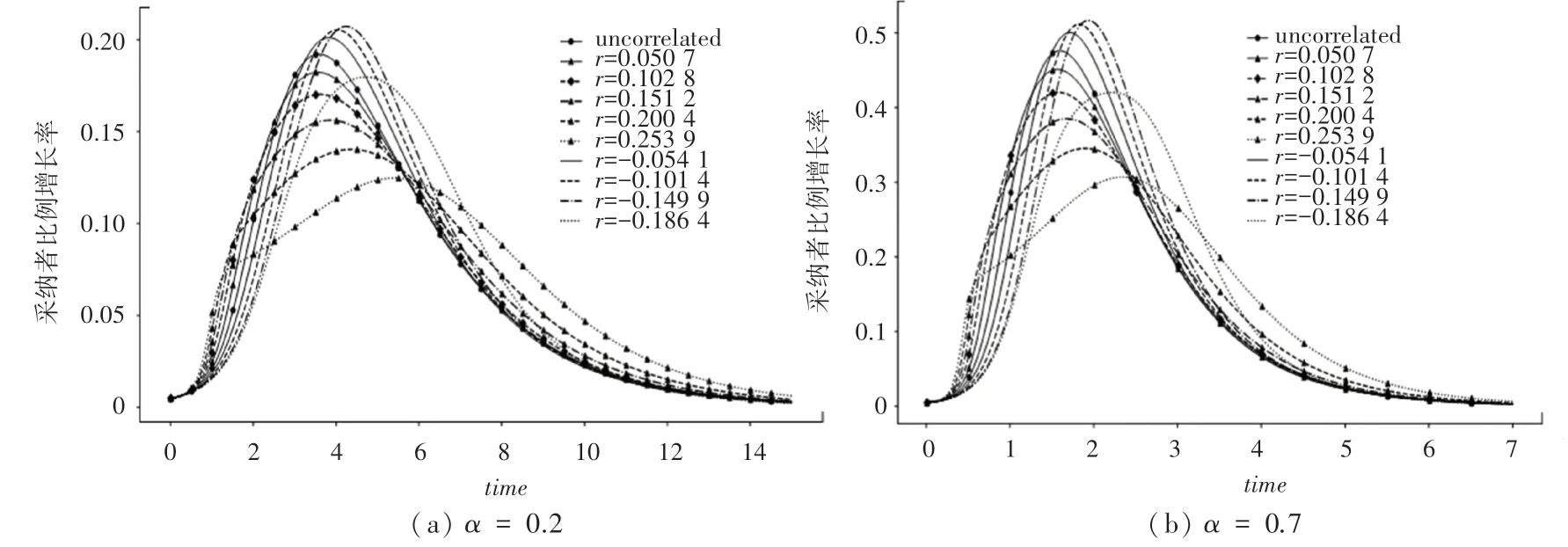
图9 不同网络中采纳者比例增长率和比例增长率时间演化图Fig. 9 Time evolution diagram of proportion growth rate and proportion growth rate of adopters in different networks

除了探究网络拓扑结构对模型的时间依赖行为影响外，对扩散速率峰值时间的影响的研究也有一定意义。 这里的扩散速率和上文提到的增长率概念相同。 扩散速率峰值时间，是指产品扩散到最高扩散速率所需要的时间。 图10 展示了不同网络结构下，创新产品扩散速率峰值时间随的变化情况。从图中可以看出，随着的增加，每个网络中的扩散速率顶峰时间均变短。 而且，在同配网络中，产品的扩散速率峰值时间随着同配混合性的增强而延长；在异配网络中，产品扩散速率峰值时间随着异配混合性的增强而延长。 此外，在∈［0149 9，0151 2］时，同配无标度网络比异配无标度网络更早达到扩散速率峰值。 并且，在较高（0200 4，0253 9）或较小（0186 4）的无标度网络中，扩散速率峰值时间远远长于其他网络。

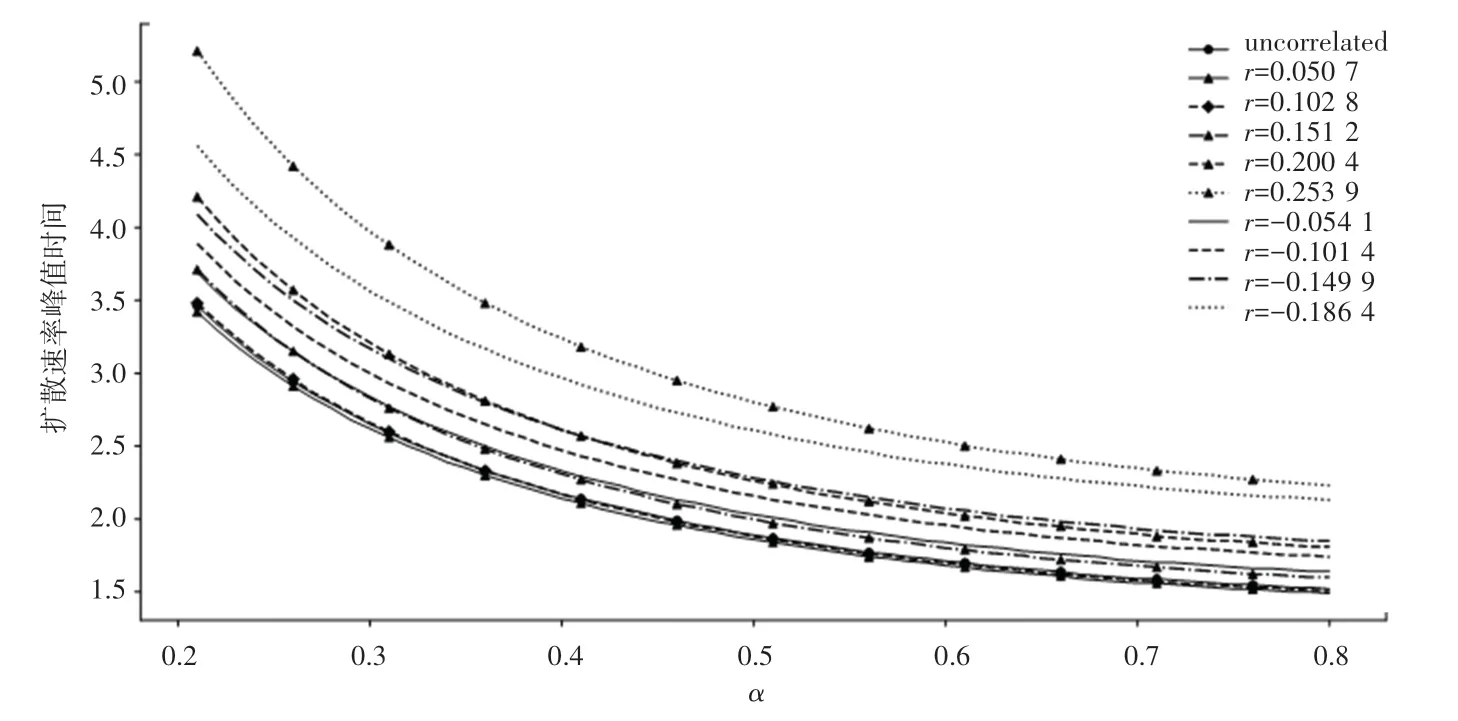
图10 不同网络中创新产品扩散速率峰值时间随α 的演化情况Fig. 10 Evolution of innovative product diffusion peak time withα in different networks

综上所述，经分析网络对创新产品扩散的影响发现：

（1）在扩散早期，同配无标度网络有利于创新产品扩散；而在扩散中期，异配无标度网络加速产品扩散。

（2）同配性混合和异配性混合都存在一个临界水平，网络的同配系数一旦超出该水平，网络就会对产品扩散产生不利影响。

（3）同配系数接近于0 的无标度网络最有利于创新产品扩散，并且对创新产品扩散的影响几乎相同。

5 结束语

本文基于Bass 模型构建了一个考虑消费者风险偏好的创新产品扩散模型，借助复杂网络理论研究创新产品的扩散动力学问题。 与以往研究相比，不仅推导了带有风险偏好的平均场方程，而且还通过数值仿真研究了个体风险偏好的影响，以及网络同配性对创新产品扩散的影响。 研究发现，创新产品扩散显著依赖于消费者的风险偏好，消费者风险偏好越高，创新产品扩散越快。 另一方面，通过分析网络拓扑结构的影响，发现同配无标度网络在早期有利于创新产品的扩散，而异配无标度网络在中期更有利于创新产品的扩散。 此外，同配系数接近于0 的无标度网络对产品扩散最有利。

基于上述研究结论，可以给出一些营销策略，为投放创新产品的企业提供决策参考。 例如，在创新产品扩散的早期，企业可以制定一些促销策略（如赠品、返利、保修策略等），以提高消费者的满意度和信任度，从而在熟人中形成良好口碑；在扩散中期，企业需要把更多的注意力放在在线社交网络上（如在新浪微博等社交平台上发布更多产品正面信息）。 这样，无论是真实的社会关系（亲人、朋友等），还是网络社交平台形成的虚拟社会关系（粉丝、网民等），都将对个人产生最大化的影响，帮助企业以较少的资本投入实现创新产品的高效扩散。