基于贝叶斯网络的地铁驾驶员行车作业人因风险分析方法

张智贤， 李 健， 刘志钢， 朱 琳

（上海工程技术大学 城市轨道交通学院， 上海 201620）

0 引 言

近年来，由于国家政策的正确指导和相关城市对规划建设轨道交通的积极探索，地铁行业的发展速度、规模和现代化水平方面均取得了很好的成绩。然而，在大力建设地铁的同时，运营事故的发生率却也在逐年上升，保证地铁运营安全成为了当下社会关注的焦点和行业内迫切需要解决的问题。 在地铁行业中，最能直接影响地铁运营安全的就是地铁的行车作业，行车作业的安全直接关系到人民群众的生命和财产安全，进而影响到地铁行业的经营效益和社会的稳定。 所以，对地铁行车作业的研究就显得尤为重要。

地铁行车作业是一个庞大的系统，涉及的岗位众多，每个岗位所承担的作业项数量及重要程度有所不同。 本文通过选取全国地铁行业中发展水平较高的上海地铁作为调查对象，并对其行车作业进行研究，发现地铁驾驶员的行车作业是所有行车岗位中作业项数量最多的，各岗位作业项数量分布情况如图1 所示。 地铁驾驶员作为直接驾驶地铁列车的操作人员，直接地影响到地铁的行车安全，因而本文将以地铁驾驶员的行车作业作为研究对象展开研究。

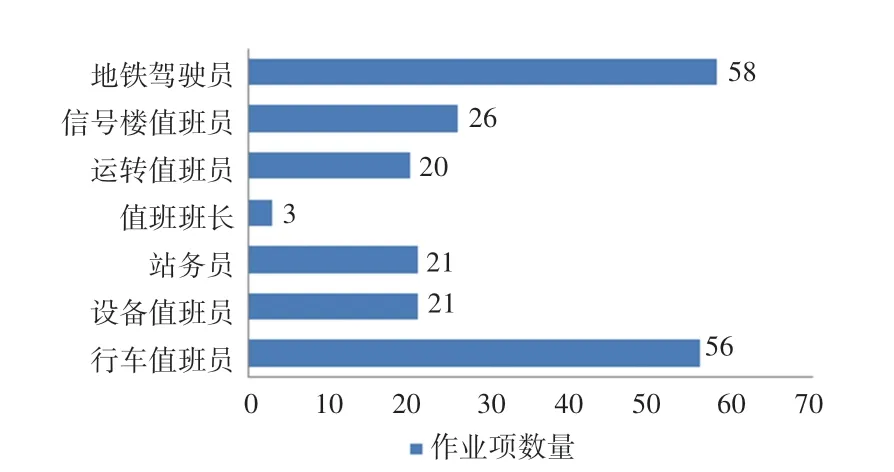
图1 地铁行车作业中各岗位作业项数量分布图Fig. 1 Distribution of the number of job items in each post in subway operation

地铁驾驶员行车作业项数量大，在行车作业时偶尔会出现操作差错和违规等不安全行为。 不仅如此，地铁驾驶员行车作业的作业环境与其他行车岗位相比也较为特殊，地铁驾驶员大多时间都需要独自在空间狭窄且光线昏暗的驾驶室里，对地铁驾驶员生理和心理上的双重影响，出现不安全行为的概率大大增加。 这些人的不安全行为通常在危险源辨识中被定义为第二类危险源中的人为因素，使得行车作业存在发生地铁运营事故的风险。 所以，本文旨在对地铁驾驶员行车作业中人为因素所带来的风险进行分析。

国内外学者对于地铁驾驶员行车作业人因风险分析的研究大多停留在对于人因风险的定性分析，常见的分析方法有经验分析法、类比法、安全检查表法以及事故统计分析法，其分析过程受研究人员主观认识的影响较大，且由于地铁驾驶员行车作业涉及内容繁多，运用例如安全检查表、事故统计分析法等方法进行风险分析时，往往要靠人工对大量数据进行分析研究，不仅效率低，还容易出错，致使得出的结果产生偏差。 基于此，本文提出一种基于贝叶斯网络的地铁驾驶员行车作业人因风险分析方法。

1 贝叶斯网络

1.1 贝叶斯网络简介

贝叶斯网络（Bayesian Network）也被称为置信网络（ Belief Networks），是依据图论和概率论作为理论核心，以有向无环图为具体表现形式，直观地描述变量之间逻辑关系和概率关系，利用概率推理技术进行数据挖掘和不确定性推理的一种理论模型，被认为是目前不确定知识表达和推理领域最有效的理论模型之一。 贝叶斯网络具体表现为一个由节点变量、有向连接边和条件概率表构成的有向非循环网络，是用来表示变量集合的连续概率分布的图形模式，是人工智能、概率理论、图论、决策理论相结合的产物。

贝叶斯网络提供了一种自然地表示因果信息的方法，用来发现数据间的潜在关系，具有描述系统多态性和复杂逻辑关系的能力，既能够对不确定性和概率性事件进行预测，还能够分析其关键致因，十分适合用于可靠性、安全性的分析与评价。 因此，贝叶斯网络被广泛应用于处理和解决具有内在不确定性的推理和决策的问题上，例如：故障检测和诊断、风险分析、概率专家系统、计算机视觉、交通管理和数据挖掘等。

1.2 贝叶斯网络的数学理论基础

其中，(B｜A) 表示在事件发生的条件下，事件B发生的概率，被称为事件B的后验概率；(A ｜B) 表示在事件B发生的条件下，事件发生的概率，被称为事件的后验概率；(B) 表示事件B发生的概率，被称为事件B的先验概率。

从公式（1）不难看出，在已知事件B的先验概率和与之对应的事件的后验概率（又称条件概率）的情况下，可以求得事件的先验概率，进而可以利用事件的先验概率反过来去推算事件B的后验概率，这就是贝叶斯网络核心的数学计算逻辑，依据贝叶斯公式对其网络结构中各结点的概率进行推理和计算，从而为处理和解决一些具有不确定性的问题提供帮助。 本文也正是利用贝叶斯网络优秀的正向和逆向推理能力，选取贝叶斯网络理论模型，对地铁驾驶员行车作业人因风险这一不确定性较强且复杂的问题进行分析。

1.3 贝叶斯网络的优势

通过对比分析其他风险分析模型，总结出贝叶斯网络的4 点优势：

（1）贝叶斯网络具有强大的处理不确定性问题的能力。 可以用条件概率表和网络拓扑结构来表示网络中各节点之间的相互关系，根据需要完成对风险分析对象正向和反向推理，计算风险存在可能引起各种事故发生的概率，推理出各种因素导致事故发生的概率，从而为风险管控和事故诊断分析提供帮助。

（2）贝叶斯网络具有较强的数据分析处理能力。 传统风险分析模型在面对数据量较大的分析对象时，暴露出其分析处理数据能力较弱的问题，而贝叶斯网络却可以利用先进的计算机技术高效地分析和处理数据，大大缩短了风险分析的时间，也降低了因数据量较大导致数据处理过程出错的概率，提高了风险分析的精度。

（3）贝叶斯网络具有动态性和可调整性。 贝叶斯网络已经成为人工智能研究中不确定性知识表示和推理的重要工具，结合先进的计算机技术，可以对贝叶斯网络进行训练，通过对训练样本数据库的学习，修正网络中各节点的概率参数，使模型得到调整和更新，与其他静态风险分析模型相比，这种具有动态性的风险分析模型所分析出来的结果更加具有时效性和准确性。

（4）贝叶斯网络是一种将多元知识图解可视化的概率知识表达与推理模型。 与传统风险分析模型不同，贝叶斯网络以图形的模式表示变量集合的连续概率分布，从而能更为直观地表达网络节点变量之间的因果关系和条件相关关系，使风险分析过程变得形象化和可视化。

1.4 贝叶斯网络的建模

运用贝叶斯网络进行风险分析，首先需构建贝叶斯网络模型，即确定网络的拓扑结构和网络中各节点因素的条件概率分布，通常把贝叶斯网络中所有节点因素的条件概率分布统称为贝叶斯网络的概率参数。 因此，贝叶斯网络的建模包括一个确定拓扑结构的定性过程和一个确定概率参数的定量阶段。 对于不同的问题，贝叶斯网络的建模方式也各有不同，主要有以下3 种建模方式：

（1）手动建模。 主要根据专家知识经验，手动建立模型的网络拓扑结构并确定概率参数，具体步骤包括：

①选取和确定节点变量；

②尝试绘制网络拓扑结构；

③定义节点状态空间；

④确定各节点的条件概率分布。

（2）数据库学习建模。 结合计算机技术，通过对训练样本数据库的学习自动生成贝叶斯网络模型，具体包括结构学习和参数学习两个步骤。 结构学习是综合先验知识，并通过学习训练样本数据库，确定较为合适的网络拓扑结构；而参数学习则是利用确定的网络拓扑结构，通过对训练样本数据库的学习，确定贝叶斯网络中各节点的概率参数。

（3）两阶段建模。 综合前两种建模方式的优点，结合专家知识经验和对数据库的学习进行贝叶斯网络建模。 建模的第一阶段是基于专家对于场景的解释和对事件之间因果关系的理解，建立初始的贝叶斯网络模型，而建模的第二阶段则是通过对训练样本数据库的学习，对贝叶斯网络模型中各节点的概率分布进行修正，使其更接近实际。 修正过程可以看成是机器学习理论中的一个学习任务，该学习任务的源信息包括初始贝叶斯网络模型和数据集合，目标是在此基础上建立更好的贝叶斯网络模型。

本文选取两阶段的建模方式构建贝叶斯网络模型，旨在构建出更加科学的模型来分析地铁驾驶员行车作业人因风险。

2 初始贝叶斯网络模型的构建

本文构建贝叶斯网络模型旨在对地铁驾驶员行车作业人因风险进行分析，而地铁驾驶员行车作业所涉及作业项数量多且复杂，若针对地铁驾驶员行车作业整体构建一个贝叶斯网络模型，分析出来的结果过于笼统。 所以，本文尝试针对每一个独立的作业项构建贝叶斯网络模型。 本文将以地铁驾驶员行车作业中“正线列车执行巡道作业”为例，具体阐述建模过程。

2.1 网络拓扑结构的构建

风险是人们对于危险源导致事故发生的可能性及后果严重程度的主观评价，本文的作业中人因风险分析，本质上是对作业中人因引发事故的可能性和后果严重程度进行分析。 所以，在构建网络拓扑结构前，先构建 事故分析的主要技术手段“事件树”，对作业中人因可能引发的事故进行分析，再将事件树转化为贝叶斯网络拓扑结构。

2.1.1 事件树的构建

事件树是将某一初始事件可能导致的事故场景和产生的多个后果加以图形化的模型，是一种从原因到结果的过程分析，其基本原理是任何事物从初始原因到最终结果所经历的每一个中间环节都有成功或失败两种可能或分支。 如果将成功作为上分支，将失败作为下分支，再分别从这两个状态开始，仍按成功或失败两种可能分析，这样一直分析下去，直到最后结果为止，最后即形成一个水平放置的树状图。

依据这一基本原理，构建“正线列车执行巡道作业”的事件树，如图2 所示。 其中，对各环节事件“成功”和“失败”状态进行了重新定义，将成功状态定义为在该环节事件中地铁驾驶员未出现不安全行为，而失败状态则定义为在该环节事件中地铁驾驶员出现了不安全行为。

图2 正线列车执行巡道作业的事件树Fig. 2 Event tree for mainline trains performing patrol operations

2.1.2 事件树的转化

事件树向网络拓扑结构的转化主要有以下3 个步骤：

（1）事件树中的每一个环节事件都对应着网络拓扑结构中的一个根节点，根据环节事件的名字对相应的根节点进行命名，各根节点的状态空间均为成功（Success）和失败（Fail）。

（2）事件树中的每一个事故后果都对应着网络拓扑结构中的一个叶节点，根据结果的名字对相应的叶节点进行命名，各叶节点的状态空间均为出现（Present）和未出现（Absent）。

（3）把上述步骤得到的根节点和叶节点用有向弧连接起来，有向弧箭头由根节点指向叶节点。

依据上述转化步骤，并利用专业的贝叶斯网络分析软件Netica，对正线列车执行巡道作业的事件树进行转化，得到如图3 所示的正线列车执行巡道作业的贝叶斯网络拓扑结构，图中各节点的信度栅均为50，说明该贝叶斯网络的概率参数还未确定。

图3 正线列车执行巡道作业的贝叶斯网络拓扑结构Fig. 3 Bayesian network topology structure of main line trains performing patrol operation

2.2 概率参数的确定

初始贝叶斯网络模型中概率参数的确定主要依据事件树和专家知识经验。 对于网络拓扑结构中各根节点的先验概率，通过地铁行业内专家的分析和讨论，确定接受调度命令（Phase1）、建立ATP 模式（Phase2）和执行正线巡道任务（Phase3）的成功概率分别为92%、96%和90%，并将概率数值输入网络拓扑结构中；而各叶节点的条件概率，则依据事件树的结构特性确定，并将确定的概率数值输入各叶节点的条件概率表（CPT）中，具体各叶节点的条件概率表如图4 所示。

最后，运用Netica 软件的网络整合功能，将构建的网络拓扑结构和确定的概率参数进行整合，得到初始的贝叶斯网络模型如图5 所示。

图4 各叶节点的条件概率表Fig. 4 Conditional probability table of each leaf node

图5 正线列车执行巡道作业的初始贝叶斯网络模型Fig. 5 Initial Bayesian network model of main line trains performing patrol operation

3 贝叶斯网络模型的修正

贝叶斯网络模型的修正主要包括对于网络拓扑结构和概率参数的修正。 由于初始贝叶斯网络中根节点和叶节点之间有较为清晰的逻辑关系，因此在网络拓扑结构上无需再进行修正，本文主要在确定的网络拓扑结构基础上，对其概率参数进行修正。概率参数的修正主要是依据训练样本数据库对贝叶斯网络进行训练，贝叶斯网络通过对训练样本数据的学习，完成对其概率参数的自我修正。

本文首先采用安全检查表法采集地铁驾驶员行车作业的现场数据，结合过往地铁驾驶员行车作业人因事故案例相关分析数据，汇总成一个原始数据库，再对原始数据库进行数据预处理，预处理过程主要包括数据审核、数据筛选以及数据排序，经过一系列处理将原始数据转换为适合贝叶斯网络学习的数据，并将数据按不同作业项的训练样本数据集分类输出，从而获取整个训练样本数据库。 获取正线列车执行巡道作业的训练样本数据集见表1，最上方有一行字符串“／ ／ ～- ＞［ CASE - 1 ］ - ＞～”，表明数据集格式为Case File Format。 本文对地铁驾驶员行车作业中每一个作业项的训练样本数据量均定为500，为了突出模型普适性，数据预处理时保留了少量有数据缺失的样本，样本缺失率设定为2%。表1 中，第一行为各节点的名称，“IDnum”列为样本编号，“∗”即为缺失数据。

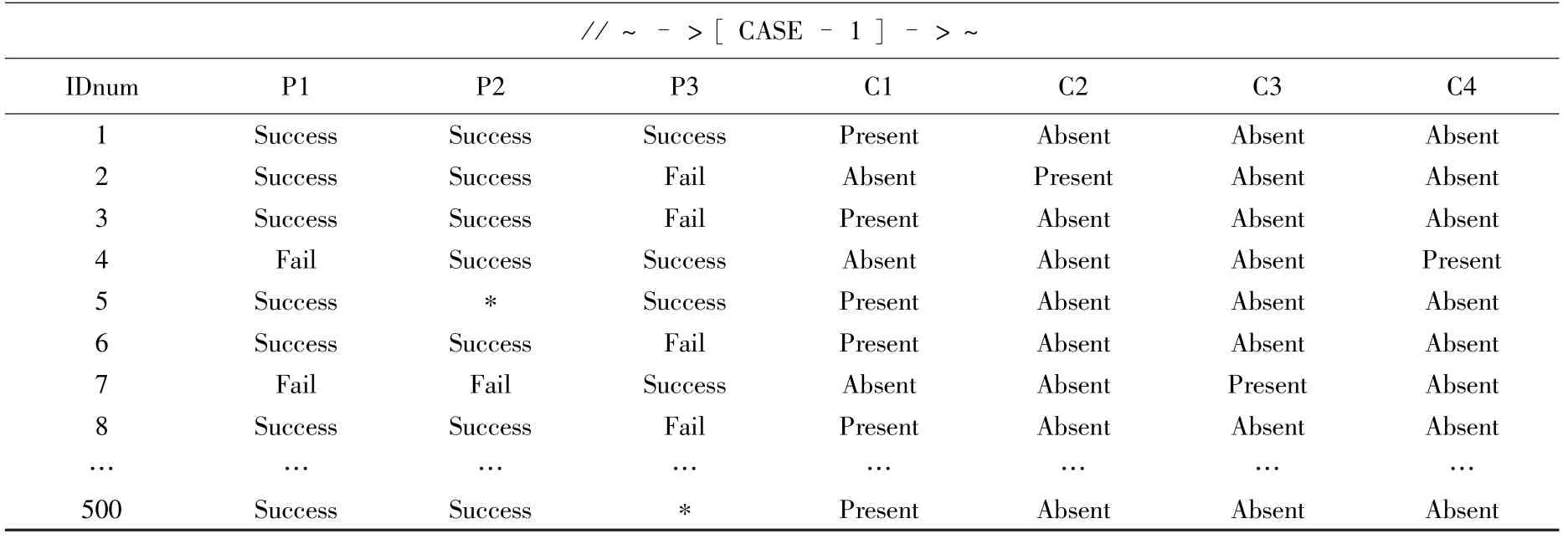
表1 正线列车执行巡道作业的训练样本数据集Tab. 1 Training sample data set of main line trains performing patrol operation

根据已获取的正线列车执行巡道作业的训练样本数据集，对其初始贝叶斯网络模型进行训练，训练过程本质上是贝叶斯网络对数据自主学习的过程。本文首先将训练样本数据集以文本文档（.txt）格式导入Netica 软件中，运用Netica 软件中的数据自主学习功能，完成了对导入数据的自主学习，同时也完成了对其概率参数的自我修正，修正后的正线列车执行巡道作业的贝叶斯网络模型如图6 所示。

图6 修正后的正线列车执行巡道作业的贝叶斯网络模型Fig. 6 Revised Bayesian network model of main line trains performing patrol operation

4 人因风险分析

本文主要依据构建出的贝叶斯网络模型，结合Netica 软件对地铁驾驶员行车作业人因风险进行分析，以“正线列车执行巡道作业”为例，阐释基于贝叶斯网络的地铁驾驶员行车作业人因风险分析过程。

首先，通过对图6 中的贝叶斯网络模型各叶节点状态空间分布进行研究，对正线列车执行巡道作业人因风险作初步分析。 在通常情况下，地铁驾驶员顺利完成正线列车执行巡道作业（C1）且作业过程中未产生人因风险的概率为87.16%，将其定义为正线列车执行巡道作业的安全概率，则正线列车执行巡道作业中存在人因风险的概率为12.84%；根据人因风险带来的事故类型对人因风险概率细分，其中人因风险引起“异物侵限”事故（C2）发生的概率为4.01%，引起“列车冲突、挤岔、撞轧”事故（C3）发生的概率为2.63%，引起“列车晚点30 min 以上”事故（C4）的概率为6.2%。

其次，依据图6 中的贝叶斯网络模型并运用Netica 软件，针对各种情况下的人因风险作进一步预测分析。 例如，已知地铁驾驶员在“建立ATP 模式”环节（Phase2）中存在不安全行为，则将贝叶斯网络中Phase2 节点变量状态设置为“Fail ＝100%”，运用Netica 软件的更新功能对整个网络的概率进行更新，得到一个新的贝叶斯网络如图7 所示。 根据图7 中各叶节点更新过后的概率，对该情况下的人因风险进行预测分析：若地铁驾驶员在“建立ATP模式”环节（Phase2）中存在不安全行为，则这些人为因素引起“列车冲突、挤岔、撞轧”事故（C3）发生的概率为93.8%，引起“列车晚点30 min 以上”事故（C4）发生的概率为6.2%。

图7 更新后的贝叶斯网络模型Fig. 7 Updated Bayesian network model

从上述人因风险分析过程中不难看出，这种贝叶斯网络风险分析模型不仅能够对一般情况下地铁驾驶员行车作业存在的人因风险进行定量化分析，还能够对各种具有不确定性情况下的作业人因风险进行预测分析，这种全面的人因风险分析能力可以为地铁行业对行车作业人因风险的管控提供帮助。 不仅如此，通过对上述人因风险分析结果的探究，发现其与实际情况高度一致，证明了基于贝叶斯网络的地铁驾驶员行车作业人因风险分析方法的可行性和实用性。

5 结束语

本文提出一种基于贝叶斯网络的地铁驾驶员行车作业人因风险分析方法，以“正线列车执行巡道作业”为例，从对贝叶斯网络模型的构建到依据模型的预测分析，详细阐释了人因风险分析的过程，证明了该方法的可行性和实用性，旨在为地铁行业提供一种全新的人因风险分析思路。 通过构建高效的贝叶斯网络风险分析模型，运用先进的计算机技术进行人因风险分析，保障地铁运营安全。 在后续研究中，将对构建出的贝叶斯网络模型的结构进行深入研究，尝试通过结构学习的方法进一步优化模型，得到更为科学的贝叶斯网络模型。