轴向变厚度星形管吸能特征及多目标优化研究

邓小林， 黄家乐

(1.梧州学院 电子与信息工程学院，广西 梧州 543002； 2.广州大学 机械与电气工程学院，广州 510006；3.厦门大学 机电工程系，福建 厦门 361005)

汽车被动安全当中的碰撞安全问题已引起社会高度关注,碰撞事故所导致的生命和财产损失促使科学家和工程师们不断研发更为先进的缓冲吸能装置以提高车辆等交通工具的耐撞性能。而随着能源短缺、环境污染等问题的日益突出，以及变厚度吸能结构在降低初始峰值载荷方面所具有的天然优势，变厚度吸能结构日益被专家重视[1-2]。前期的大量调研发现，变厚度薄壁吸能结构通常采用以下三种方式来实现，第一种方式为沿薄壁结构轴向改变壁厚所得到的轴向变厚度薄壁结构。如：Yao等[3]提出的一种具有轴向变厚度功能梯度圆管结构，他们对该结构在轴向压缩下的耐撞性进行了详细研究，同时开展了该结构的多目标优化。Mohammadiha等[4]也提出了一种轴向变厚度的圆管结构，与Yao等的研究不同的是，他们所提出的结构轴向厚度变化呈线性分布，并且研究的加载方式为斜向载荷加载。Sun等[5]和Li等[6]提出了一种壁厚沿轴向呈功能梯度变化的方管，并对该管在轴向载荷作用下的耐撞性和优化开展了系统的分析，同时，对该结构与锥形管的耐撞性进行了对比。此外，Li等[7]还提出了一种壁厚沿轴向呈功能梯度变化的圆管，并对所提出的功能梯度圆管与锥管的耐撞性进行了对比研究，他们的研究充分表明，功能梯度薄壁管在能量吸收和初始峰值载荷这两项指标上都得到了有效改善。Baykasoglu等[8]则对轴向变厚度的圆管、方管和六边形管在多种加载角度下的耐撞性开展了对比研究，相比其对应的均匀壁厚管，变厚度管的比能量吸收最高提升了93%。而近年来，将多胞结构与轴向变厚度结构相结合的研究也陆续被研究和报道，如Pang等[9]提出的具有轴向变厚度的多胞方管以及Chen 等[10]提出的轴向变厚度八角多胞管状结构。第二种方式则是通过将薄壁结构的横截面不同部位分配不同厚度来得到横向变厚度的薄壁结构。包括Zhang等[11]、Fang等[12]、Qin等[13]都对横向变厚度的薄壁结构开展了相关研究，他们的研究也都证实了此类结构在能量吸收方面的优越性。第三种方式为两端壁厚较薄而中间壁厚较厚的变厚度薄壁结构[14]，此类结构主要应用于抗横向冲击，通过将受载荷冲击点的位置分配更厚的壁厚以达到更强抵抗横向载荷的能力。

横截面形状对薄壁结构的能量吸收起着重要的作用，Wierzbicki等[15]研究表明，金属薄壁管的能量吸收主要由塑性铰处的弯曲变形能和面内薄膜变形能构成，而多边形管的折角附近的弯曲和薄膜变形最为剧烈。因此，多边形管的横截面折角的数量很大程度上决定了结构的能量吸收性能。Yamashita等[16]开展了边数从4～96的正多边形管的轴向压缩性能，研究发现正多边形管的抗压强度随着角数的增加而增加，但当截面边数大于11后，其吸能趋于饱和。这主要因为随着边数的增加，折角的角度也相应增大，而夹角处于90°～120°时具有最好的吸能效果。然而，常规的凸多边形管无法保证在折角数目增加的同时，其夹角又刚好处于90°～120°内。因此，仅靠单纯的增加角的数目并不能有效提高多边形管的能量吸收性能。针对上述问题，Tang等[17]通过将折角内凹化，提出了一种新型的非凸截面管，该结构能保证在增加截面折角数量的同时又能保证其夹角为90°，从而有效提高了能量吸收性能。值得指出的是，星形管也可以看作是一种常规多边形内凹化后的非凸截面管。前期研究中，Fan等[18]采用试验和数值仿真方法对星形管在轴向准静态压缩下的耐撞性开展了研究，研究发现星形管相比相同角数的正多边形管具有更高的能量吸收能力。我们在前期也对星形管在轴向冲击下的耐撞性开展了系统研究[19]，在此基础上，对不同加工方式对星形管耐撞性的影响以及轴向压缩下的平均载荷的理论公式进行了推导[20]。研究发现，星形管具有很强的抗轴向冲击能力，但也存在载荷一致性较差、初始峰值载荷过大的不足。

因此，该论文将星形管的较高能量吸收特征和变厚度结构的较低初始峰值载荷相结合，创新性的提出一种新型的轴向变厚度星形管，以望综合改善比能量吸收和初始峰值载荷这两项关键耐撞性指标。前面的大量调研尚未发现国内外有轴向变厚度星形管的研究报道，该论文通过对其开展系统性的耐撞性分析和多目标优化研究，为轴向变厚度能量吸收结构的创新设计提供参考。

1 材料和方法

1.1 几何描述

所提出的轴向变厚度六角、八角和十角星形管的几何结构和有限元模型，如图1所示。大量专家和学者对轴向变厚度薄壁吸能结构的耐撞性研究已充分证实冲击端分配较薄的壁厚更有利于降低结构的初始峰值载荷。因此，这里将较薄的壁厚tmin配置在轴向变厚度星形管的冲击端，较厚的壁厚tmax配置在固定端，冲击端与固定端之间的壁厚则按式(1)线性增加。

(1)

式中，tx为距离冲击端距离为x位置处的壁厚。通过式(1)可以看出，当k=0时，结构即变成了均匀壁厚的等壁厚星形管。容易得知，等壁厚星形管的壁厚如式(2)所示。式(1)中的k为轴向厚度变化系数，该论文中的tm始终保持为1.2 mm，通过改变tmin和tmax，即可得到不同的轴向厚度变化系数k。

(2)

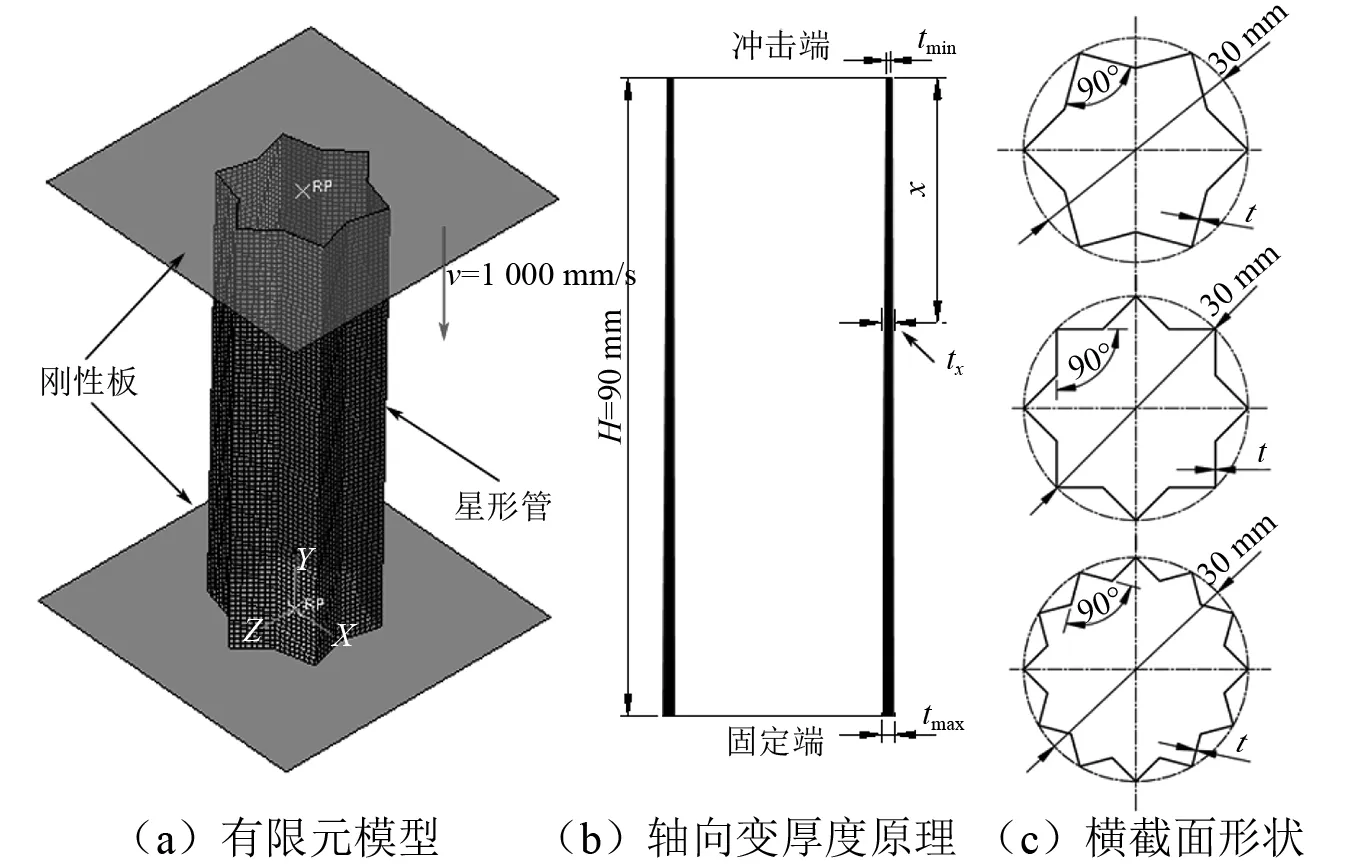
图1 几何结构设计和有限元模型Fig.1 Geometric structure design and finite element model

1.2 耐撞性评估指标

通常情况下，能量吸收(energy absorption，EA)、比能量吸收(specific energy absorption，SEA)、初始峰值载荷(Fmax)和冲击载荷效率(crush force efficiency，CFE)常被用于结构的耐撞性评估，公式如式(3)～式(5)所示。

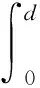
(3)

(4)

(5)

式中：F(x)为结构的瞬时冲击力；Fmax为结构的初始峰值载荷，对于轴向冲击载荷，初始峰值载荷通常为冲击初始阶段的第一个波峰值；d为结构的冲击距离；m为结构的质量;Fm则为结构在冲击过程中的平均冲击载荷，用式(6)表示。通常而言，较高的EA,SEA,CFE和较低的Fmax，意味着结构具有较好的耐撞性能。

(6)

1.3 有限元模型构建及验证

1.3.1 有限元模型

轴向变厚度星形管数值模型构建及仿真采用软件ABAQUS/Explicit开展，构建的有限元模型如图1(a)所示。轴向变厚度星形管置于上下两刚性板之间，为了提高分析效率，参考文献[21]，上刚性板以固定速度1 000 mm/s垂直向下冲击，冲击距离为星形管高度H的80%，即72 mm。星形管底端与下端刚性板绑定，同时限制下端刚性板的所有自由度，以确保在冲击过程中下端刚性板为固定状态。星形管有限元模型使用四节点减缩积分壳单元模拟，为了确保收敛，沿厚度方向采用5个积分点。模型包含自身施加通用接触算法，摩擦因数取0.3[22]。星形管的材料使用AA6061 T4，之前研究已对该材料属性进行了测试，属性如图2所示。同时，归因于铝合金AA6061T4的应变率非敏感性[23-24]，仿真过程中忽略应变率效应。

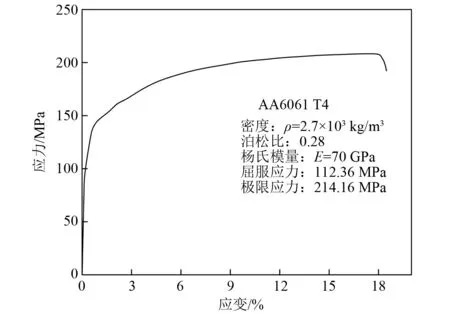
图2 AA6061 T4的应力-应变曲线和材料属性Fig.2 Stress-strain curve and material properties of AA6061 T4

需要指出的是，尽管研究的是轴向变厚度星形管，但在1.1节分析的时候已然发现，等壁厚星形管其实是k=0的一种特殊的轴向变厚度星形管。前期我们已对星形管的试验和有限元仿真进行了验证[25]，得到的变形模式和能量吸收曲线如图3所示。考虑到该论文用的所有仿真设置、边界条件和载荷加载方式等，都与2016年Liu等的研究是完全一致的，因此，这里所采用的数值仿真模型可用于轴向变厚度星形管的有限元分析。

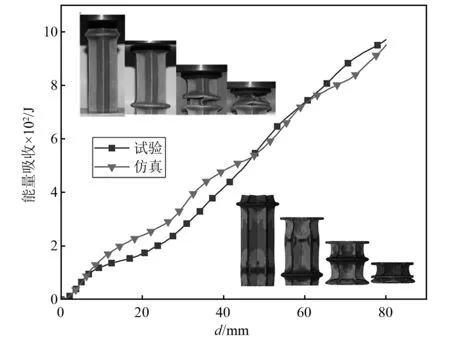
图3 星形管的试验和仿真验证Fig.3 Numerical model verification of star-shaped tube

为了测试不同网格尺寸对数值仿真结果的影响，对1.0 mm，1.5 mm,2.0 mm,2.5 mm共4种不同网格尺寸的六角星形管(k=0)进行了测试，结果如表1所示。可以看出，不同网格尺寸的能量吸收和初始峰值载荷值不同，尤其是2.5 mm的网格尺寸相比1.0 mm的网格尺寸的耐撞性数值相差较大。而当网格尺寸减小到1.5 mm时，相比1.0 mm的网格尺寸的能量吸收和初始峰值载荷之间的偏差则降为2.61%和1.14%，差距都在5%以内。考虑到网格尺寸划分过细，会耗费极大的计算资源，因此，后续的数值仿真网格尺寸选用1.0 mm。

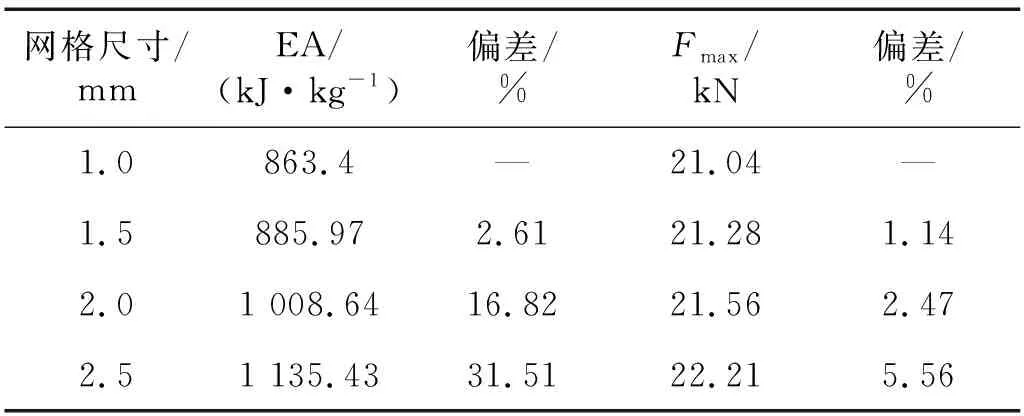
表1 网格测试结果Tab.1 Mesh test results

1.3.2 分层测试

星形管在ABAQUS/Explicit里采用的是壳单元模拟，而壳单元其实是薄壁管的中面。这里，通过将星形管沿轴向拆分成高度相等的若干层，并通过对不同的层赋予不同的厚度，以间接的实现轴向变厚度。明显的，拆分的层数越多，结构的壁厚沿轴向变化就越均匀。但考虑到计算资源消耗，这里，将六角星形管(k=1.2，tm=1.2 mm)分别拆分成9层、15层和45层，拆分方式见图4(a)，测试结果如图4(b)和图4(c)所示。从图4(c)的耐撞性数据可以看出，15层和45层的力-位移曲线和能量吸收曲线几乎完全一致。压缩到72 mm时的能量吸收分别为882.33 J和859.99 J, 15层相比45层的能量吸收仅相差2.6%，初始峰值载荷则分别为9.95 kN和10.38 kN，两者相差也仅为4.14%。图4(b)变形模式图也表明15层和45层的变形终态具有很好的一致性。因此，采用15层的分层方式能完全满足仿真分析要求。

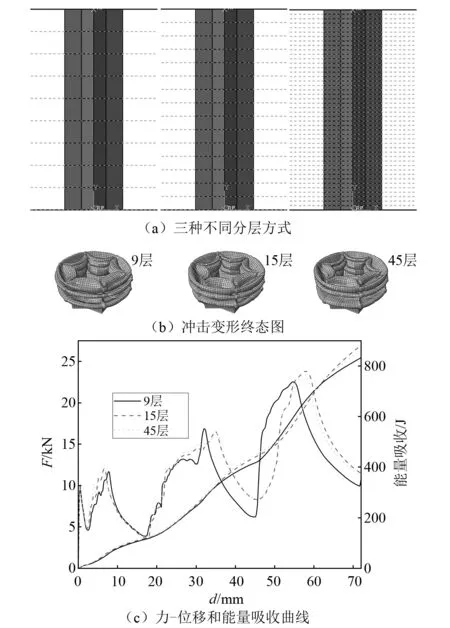
图4 不同分层的有限元仿真结果Fig.4 Finite element simulation results of different layers

前期，采用15层的分层方式与文献[26]的试验开展了轴向变厚度圆管的数值仿真和试验对比分析，结果如图5所示[27]。对比结果表明，数值仿真和试验的初始峰值载荷分别为16.45 kN和16.05 kN，两者相差仅为2.49%。压缩到80 mm时的能量吸收分别为963.19 J和963.13 J，两者几乎完全一致。因此，所采用的分层方法可适用于后续的有限元数值仿真。

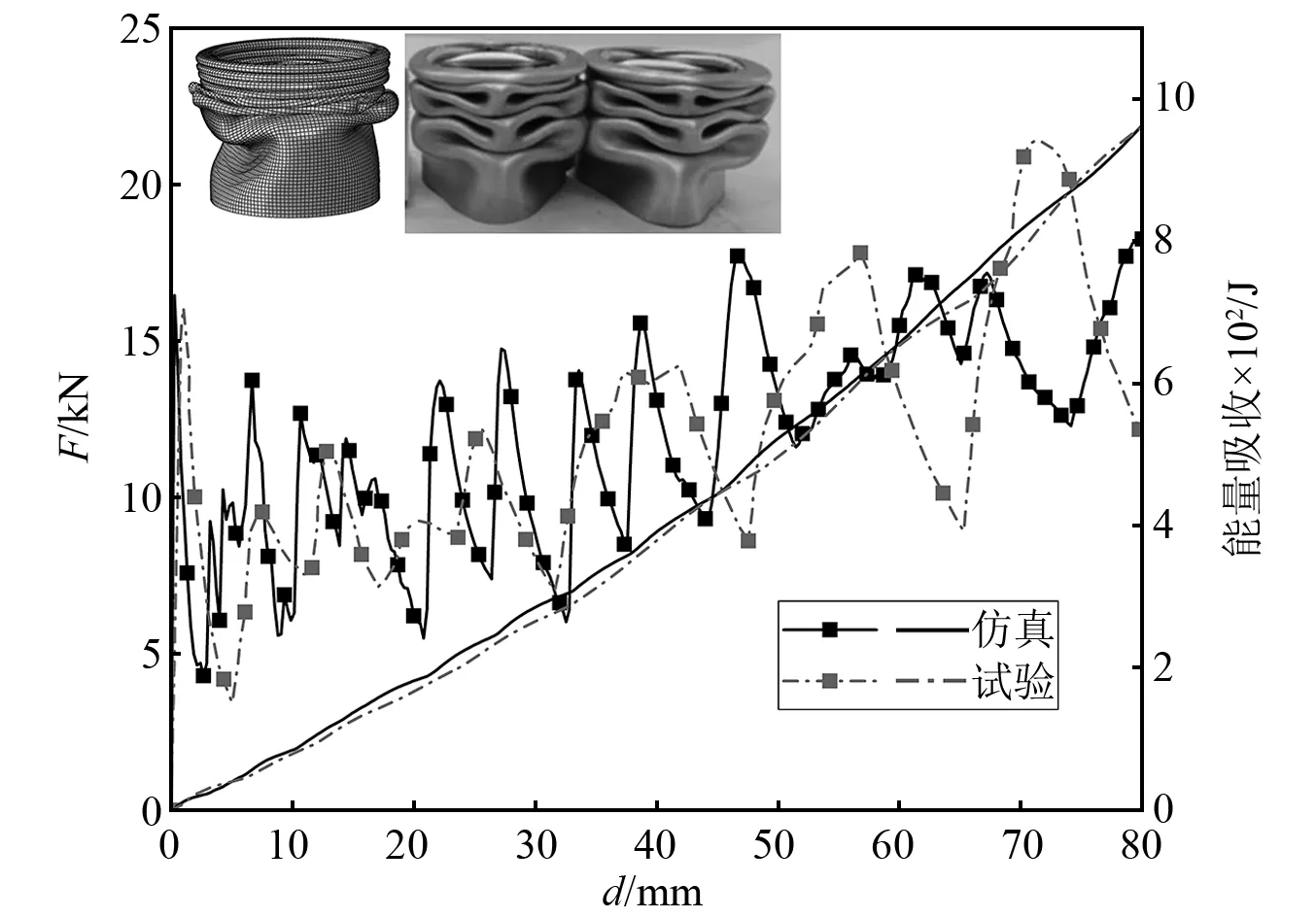
图5 轴向变厚度圆管的轴向压缩试验和数值仿真对比Fig.5 Comparison of experimental and numerical simulation results of axially variable thickness circular tube

2 耐撞性结果及讨论

为了方便后续描述，分别采用S6、S8和S10代表六角、八角和十角星形管。对S6、S8和S10在不同轴向厚度变化系数下的耐撞性开展了有限元仿真分析，结果如表2所示。

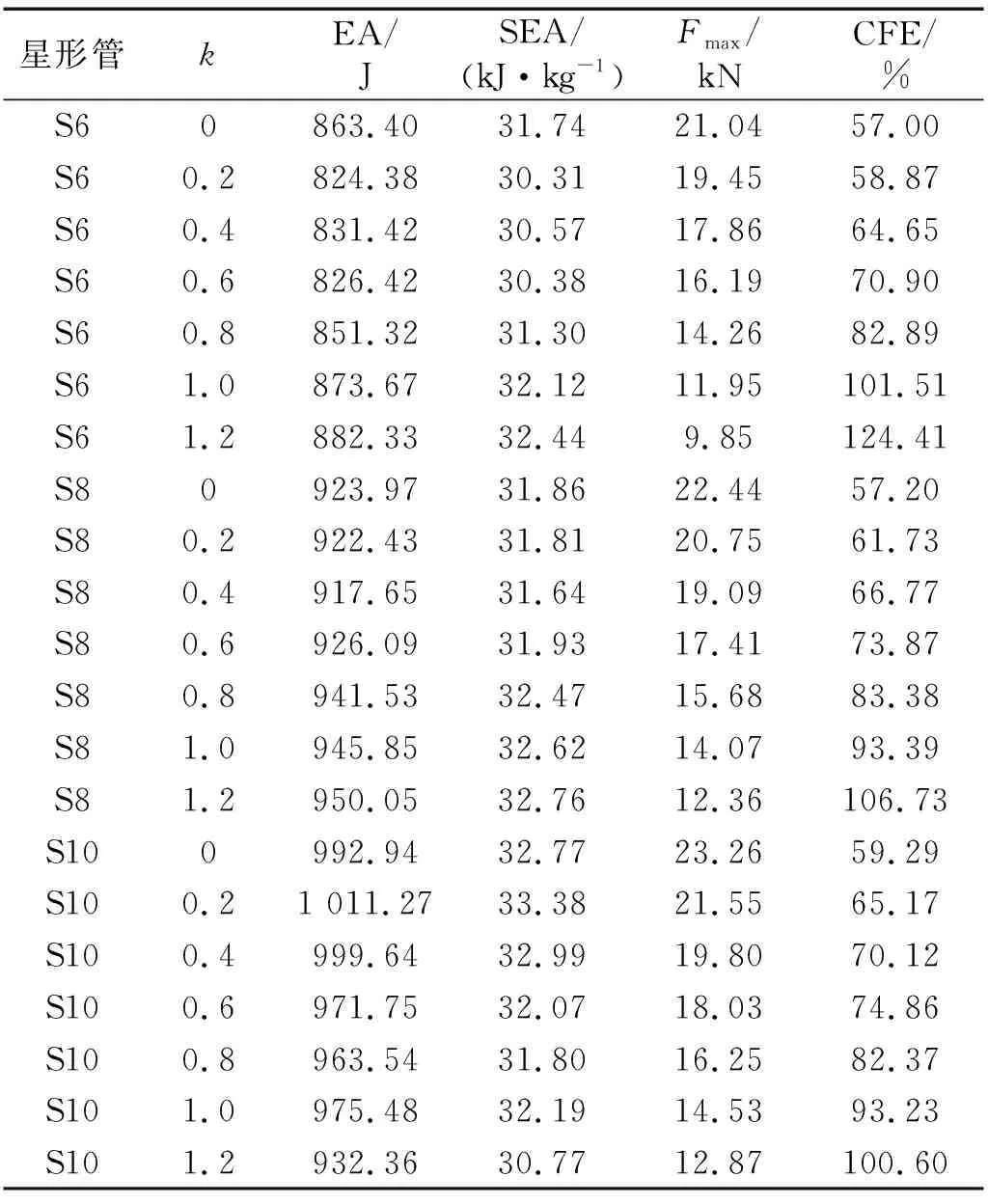
表2 不同轴向厚度变化系数的六角、八角和十角星形管的结构参数和耐撞性数据Tab.2 Structural parameters and crashworthiness data of hexagonal, octagonal and decagonal star-shaped tubes with different axial variation coefficients

2.1 变形模式

图6～图8为六角、八角和十角星形管在轴向压缩下的变形模式。为了更好的对结构的压缩变形终态的褶皱和褶皱波长进行对比分析，图9给出了变形终态及其横截面视图。

通过图6～图8可以看出:当k=0时，不同星形管的第一个褶皱产生位置都是靠近固定端;而当k>0时，不同角数的星形管的第一个褶皱产生的位置都变成了靠近冲击端处。这主要是因为当k>0时,意味着冲击端的壁厚更薄，从而使结构在靠近冲击端处更易于被压溃，这也使结构在整个压缩过程中产生了较为理想的渐进式压溃变形。

通过图9可以看出，不同角数的星形管都产生了3个褶皱。随着角数和轴向厚度变化系数的增加，第3个褶皱的不规则性开始显现，尤其是十角星形管的第3个褶皱。这主要归因于两个方面：一方面是角数的增加，结构抗轴向抵抗能力增强，使结构在轴向压缩下的不稳定性增加；另一个方面是随着k的增加，靠近冲击端的壁厚更厚，从而使结构在产生第3个褶皱的时候，进一步增加了结构塑性变形的不稳定性。通过他们的横截面视图也可以看出，第1个和第2个褶皱相对规则，并且第1个褶皱的波长也相对较短。而第3个褶皱的波长和不规则性明显增加。

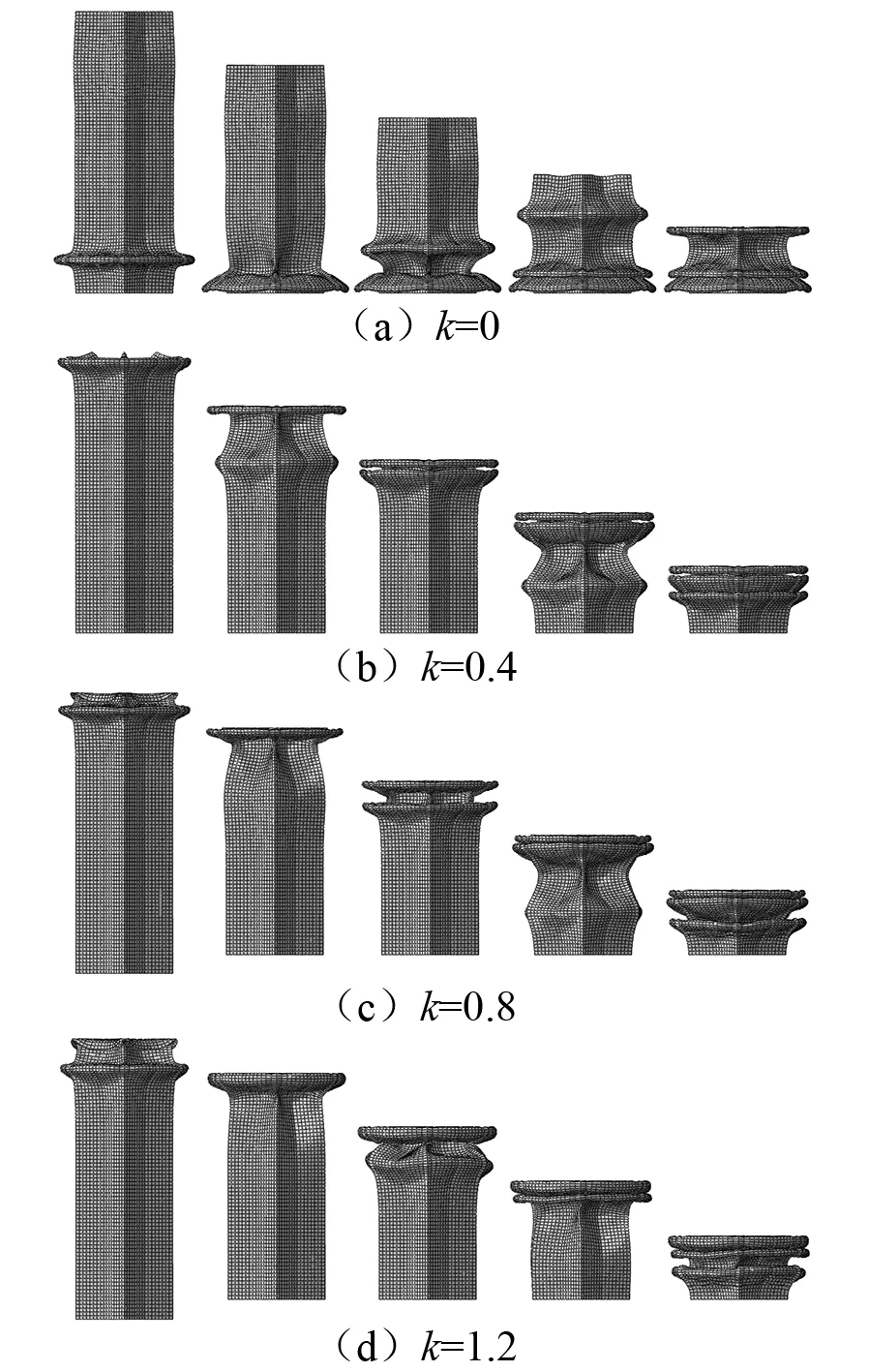
图6 六角星形管的变形模式Fig.6 Deformation mode of the hexagonal star-shaped tubes

图7 八角星形管的变形模式Fig.7 Deformation mode of the octagonal star-shaped tubes

图8 十角星形管的变形模式Fig.8 Deformation mode of the decagonal star-shaped tubes

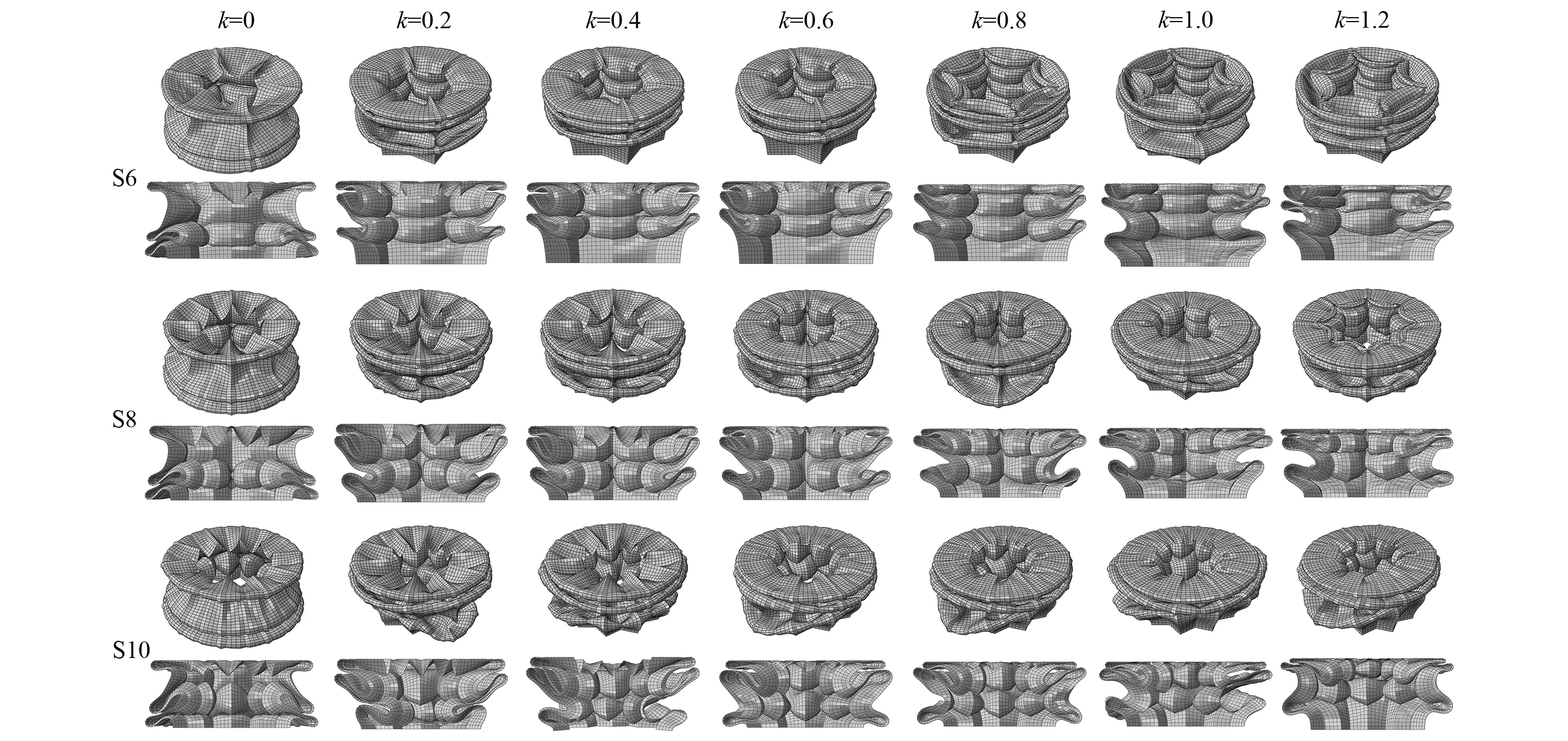
图9 六角、八角和十角星形管变形终态及其横截面剖视图Fig.9 The final deformation state and cross-sectional view of the hexagonal, octagonal and decagonal star-shaped tubes

2.2 力-位移和能量吸收情况

图10为星形管轴向冲击下的作用力和能量吸收情况。可以清楚的看出，随着k值的增加，初始峰值载荷不断变小，k值越大，结构的初始峰值载荷也越低。同时，通过2.1节的变形模式分析也可知，k值较大的星形管在靠近冲击端处的壁厚更薄，相应的参与塑性变形的结构质量也越少，这也意味着k值较大的星形管在冲击的前半段的能量吸收较差。通过能量吸收曲线图可以证实，k=0的星形管在前半段表现出了较高的能量吸收。k>0的星形管的能量吸收优势在冲击的后半阶段才开始显现。考虑到优良的吸能结构应具有较低的初始峰值载荷和较高的能量吸收。因此，所提出的轴向变厚度星形管相比常规的等壁厚星形管在降低初始峰值载荷方面具有很大的优越性。

2.3 耐撞性数据分析

图11为星形管各项关键耐撞性指标数据。通过图11(a)可以看出，十角星形管的能量吸收要好于八角和六角星形管。这主要因为十角星形管的截面角数更多，在轴向冲击下能耗散更多的能量。但需要指出的是，十角星形管的质量也更大，这样就使结构的另一项关键的耐撞性指标比能量吸收并不优于八角和六角星形管。通过图11(b)可以看出，八角星形管在k=0.8,k=1.0和k=1.2时的比能量吸收都明显优于十角星形管，甚至六角星形管在k=1.2时的比能量吸收都高于十角星形管。

图11(c)则为结构的初始峰值载荷情况。可以看出，结构的初始峰值载荷随着角数的变少和轴向厚度变化系数的增加而减小。这主要是因为角数的减少，降低了结构的抗轴向冲击能力，而轴向厚度变化系数的增加，使结构靠近冲击端的壁厚变得更薄，冲击过程中更易于发生塑性变形，从而使结构的初始峰值载荷降低。

图11(d)则为结构的冲击载荷效率情况。可以看出，轴向厚度变化系数越大，结构的冲击载荷效率越高。这主要因为冲击载荷效率是结构的平均冲击载荷与初始峰值载荷的比值。轴向系数的增加，大幅度降低了结构的初始峰值载荷，从而使结构的冲击载荷效率得到有效提升。

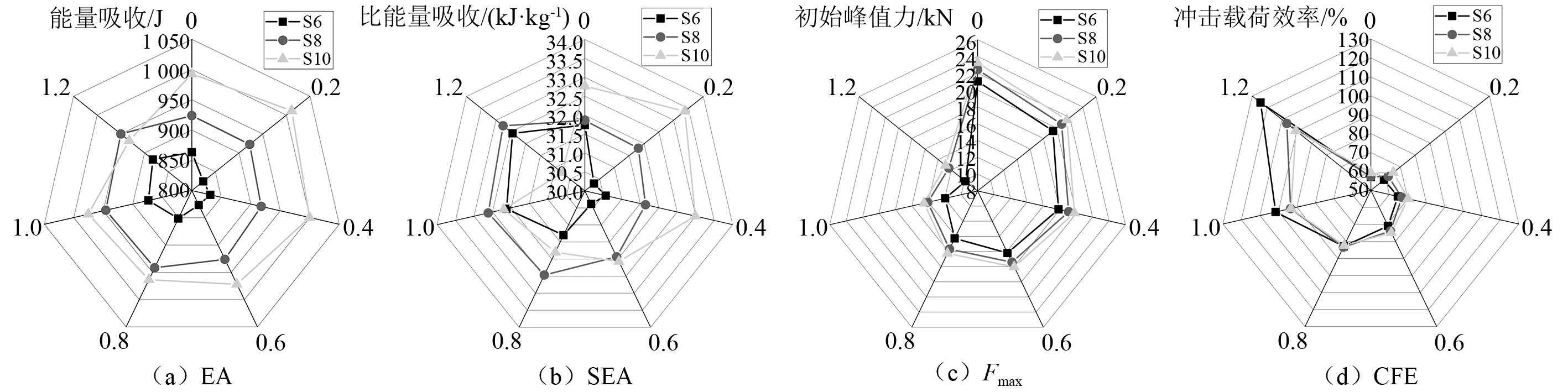
图11 耐撞性数据Fig.11 Crashworthiness data

3 不同星形管在相同质量下的耐撞性研究

本节主要研究不同角数和轴向厚度变化系数的星形管在保持相同质量时的作用力和能量吸收情况。以壁厚1.2 mm的六角等壁厚星形管的质量为基准，通过改变八角和十角星形管的壁厚，以得到不同角数星形管具有相同的质量。表 3即为星形管在相同质量下的耐撞性数据，图12则为结构的能量吸收和作用力情况，图13则为结构的耐撞性数据。

图13(a)为结构的能量吸收情况。对能量吸收而言，当k<1时，不同角数的星形管的能量吸收相差不大，相对偏差都在7%以内。而当k=1.2时，不同星形管的能量吸收具有较大的差异，八角星形管具有最好的能量吸收能力，其相比六角星形管提升了11.77%，而十角星形管则相比六角星形管降低了17.63%。

图13(b)为结构的初始峰值载荷情况。从图可以明显看出，不同种类的星形管的初始峰值载荷总体上呈现出随k值的增加而减小，而不同k值的不同角数星形管的初始峰值载荷相差并不大，大部分都在5%以内，相差最大的八角星形管(k=1.2)相比其对应质量的六角星形管(k=1.2)也仅为5.45%。

图13(c)则为结构的冲击载荷效率情况。相同质量不同角数的星形管的冲击载荷效率随k值的增加而增加。所有的星形管冲击载荷效率在k>1.2时都超过了100%，这也就意味着平均冲击载荷超过了结构在冲击初始阶段时的峰值载荷。而k<1.2时，八角和十角星形管相比六角星形管的冲击载荷效率的相对偏差都在9%以内。当k=1.2时，十角星形管的冲击载荷效率相比六角星形管降低了17.75%，这主要是因为其能量吸收出现了大幅度下降，导致结构的冲击载荷效率出现了较大下降所致。

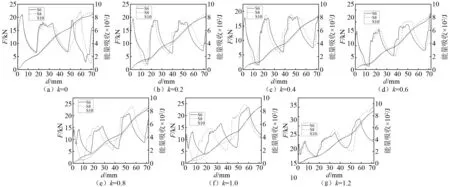
图12 相同质量星形管的力-位移和能量吸收Fig.12 Force-displacement and energy absorption of star-shaped tubes under the same mass

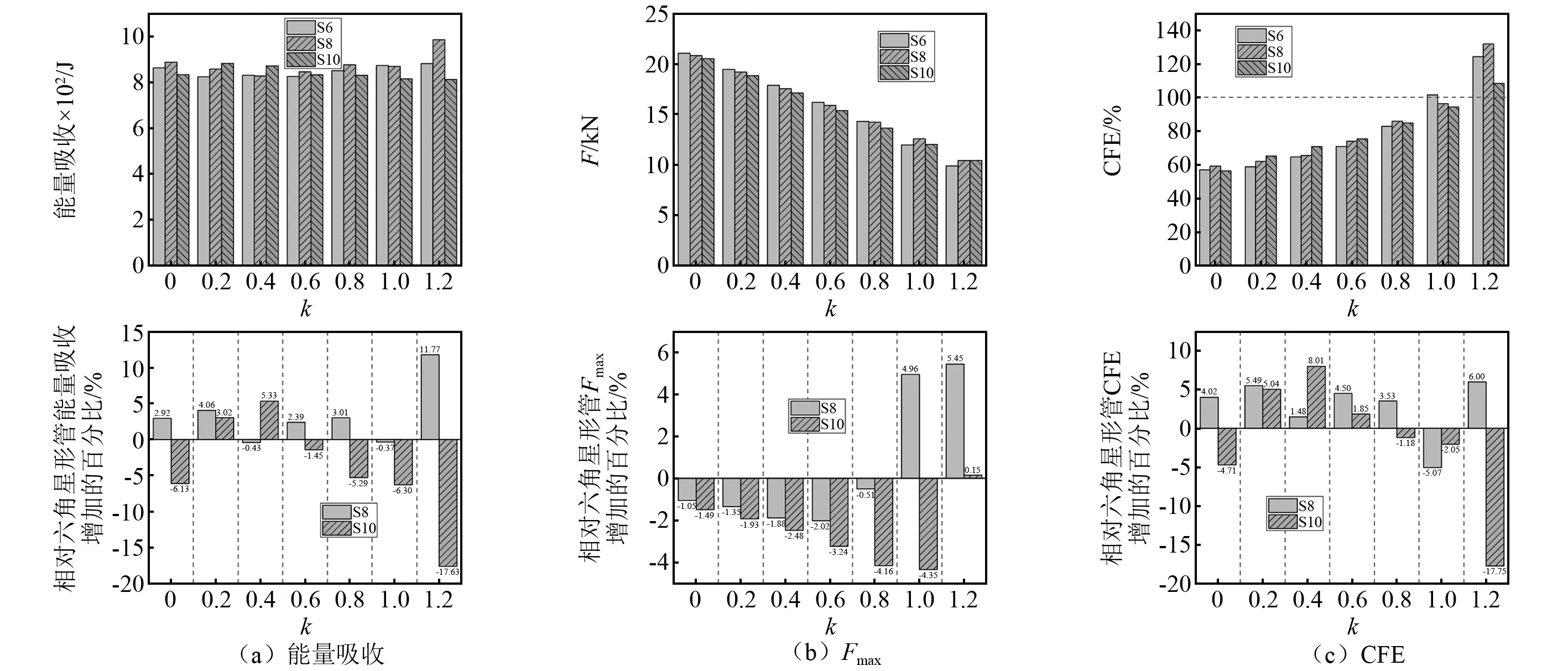
图13 相同质量星形管的耐撞性数据Fig.13 Crashworthiness data of star-shaped tubes under the same mass

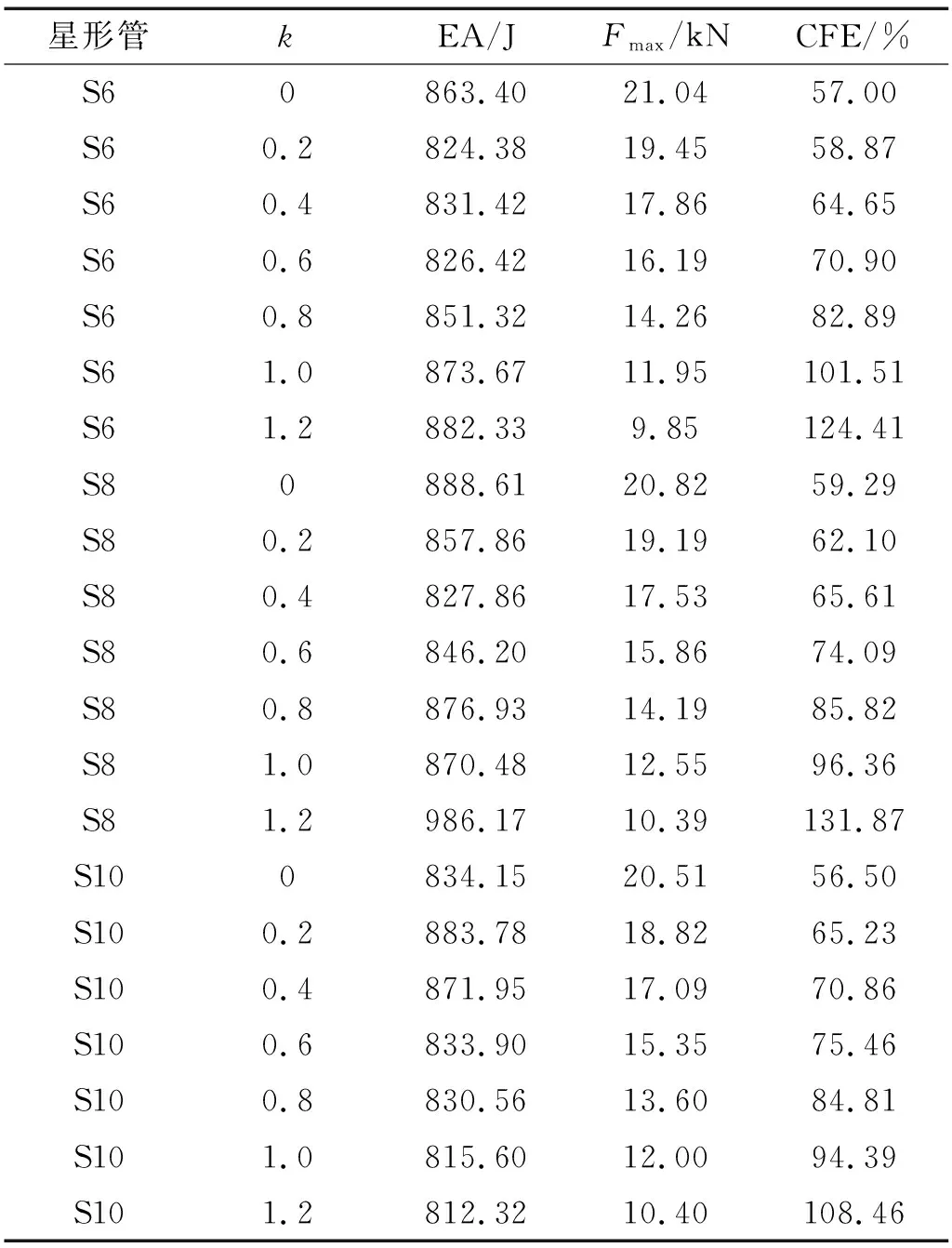
表3 不同星形管在相同质量下的耐撞性数据Tab.3 Crashworthiness data of different star-shaped tubes under the same mass

4 多目标优化

通过前面的分析可以发现，轴向厚度变化系数是影响结构耐撞性能的重要参数。这里，将轴向厚度变化系数k作为优化参数，比能量吸收和初始峰值载荷作为优化目标，对六角、八角和十角星形管开展多目标优化。优化函数如式(7)所示

(7)

考虑到星形管在轴向冲击下的变形为非线性塑性大变形，因此，这里参考之前的多目标优化方法[28-29]，通过借助代理模型来得到结构的最优设计。构建代理模型的样本点使用全因子试验方法确定，对k从0～1.2按0.5的间距取值，共得到25个样本点。构建代理模型的方法使用径向基神经网络模型，该模型具有很强的逼近复杂非线性函数的能力，同时又具备学习速度快，以及极好的泛化能力。多目标优化则采用第二代非支配排序遗传算法进行，得到的优化结果如图14所示。

通过图14可以看出，十角星形管的Pareto 前沿覆盖的范围远远超过六角和八角星形管。从降低初始峰值载荷角度而言，显然六角星形管更有优势，它的Pareto前沿的最低初始峰值载荷可达到9.79 kN,而八角和十角星形管的最低初始峰值载荷则分别为12.29 kN和12.73 kN。但同时也要看到，六角星形管的Pareto前沿的比能量吸收最大值仅为32.21 kJ/kg，而八角和十角星形管则分别达到了33.23 kJ/kg和34.02 kJ/kg，十角星形管从提升结构的比能量吸收角度出发更有优势。但值得指出的是，十角星形管的比能量吸收的提升是以牺牲结构的初始峰值载荷为代价。这里以八角和十角星形管对比为例进行说明，当八角星形管的比能量吸收最大值为33.23 kJ/kg时，结构的初始峰值载荷为12.37 kN，而十角星形管比能量吸收为33.26 kJ/kg时(考虑到Pareto前沿为离散点，选择了一个与八角星形管的33.23 kJ/kg接近的前沿点)，其初始峰值载荷达到了20.35 kN，十角星形管相比八角星形管的初始峰值载荷提高了64.51%。因此，综合考虑比能量吸收和初始峰值载荷这两项指标，显然八角星形管更具有耐撞性优势。

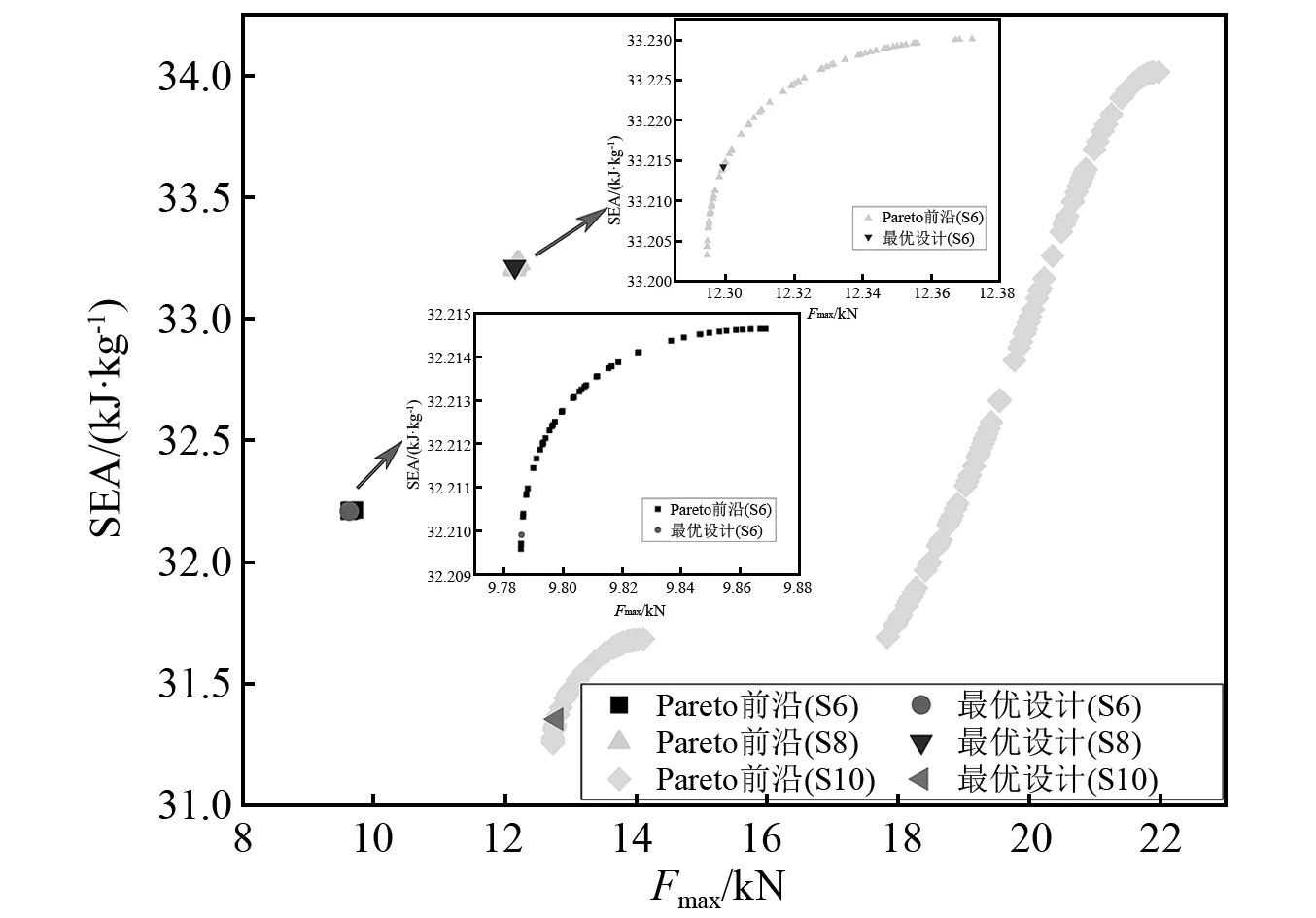
图14 多目标优化结果Fig.14 Multi-objective optimization results

这里，使用ABAQUS/Explicit对星形管的3个最优设计进行了数值仿真，以验证多目标优化结果的准确性。验证结果如表4所示，可能看出，采用多目标优化所得到的结果和ABAQUS/Explicit数值仿真的结果误差最高仅为4.08%，所有的误差都在5%以内，充分说明了优化结果的准确性。

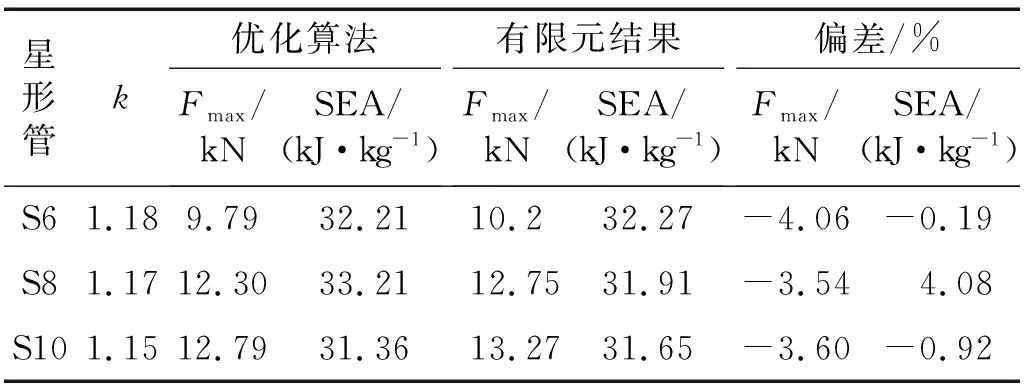
表4 优化结果验证Tab.4 Verification of optimization results

表5给出了最优设计和k=0.6的原始设计之间的耐撞性数据对比。可以看出，除了十角星形管的比能量吸收之外，其他3个最优设计解的比能量吸收和初始峰值载荷都得到了有效改善。必须强调的是，尽管十角星形管的比能量吸收降低了2.23%，但其初始峰值载荷降低高达29.07%。值得指出的是，六角星形管的最优设计相比其原始设计的比能量吸收在提高6.02%的基础上，初始峰值载荷还降低了39.56%。因此，以上都充分说明了采用多目标优化所得到的最优设计的结构耐撞性得到了有效提高。

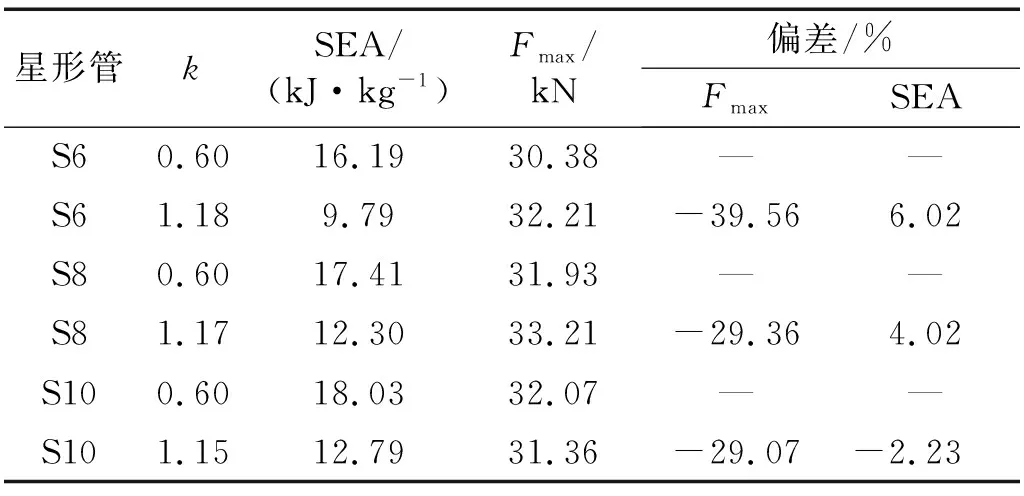
表5 最优设计与原始设计的对比Tab.5 Comparison of optimal design and original design

5 结 论

将星形管与轴向变壁厚结构相结合，提出了一种新型的轴向变厚度星形管，采用验证后的有限元数值模型开展了该结构的耐撞性研究，得到的结论如下：

(1)不同角数k=0的星形管的第1个褶皱都是在靠近固定端产生，而k>0的星形管的第1个褶皱产生的位置则为冲击端，不同角数的星形管都产生了3个褶皱，并随着角数和轴向厚度变化系数的增加，第3个褶皱的变形不规则性以及波长都相应增加。

(2)星形管的初始峰值载荷随着角数的变少和轴向厚度变化系数的增加而减小，冲击载荷效率则随着轴向厚度变化系数的增加而增加。k>0的星形管在冲击的前半阶段的能量吸收较差，十角星形管的能量吸收要好于八角和六角星形管，所提出的轴向变厚度星形管相比常规的等壁厚星形管在降低初始峰值载荷和提升结构冲击载荷效率方面具有很大的优势。

(3)相同质量、不同角数和轴向厚度变化系数的星形管耐撞性研究表明，当k<1时，不同角数的星形管的能量吸收相差不大，当k=1.2时，结构的能量吸收具有较大的差异，八角星形管在相同质量条件下具有最好的能量吸收能力。

(4)多目标优化结果表明，与原始设计相比，最优设计的比能量吸收最大提升了6.02%，初始峰值载荷最高减少了39.56%，多目标优化得到的最优设计相比原始设计的耐撞性得到了有效改善。