基于解析模态分解的极小宽深比液体晃动非线性参数辨识及试验方法

李海东， 李 龙， 侯凯宇， 史晓鸣， 夏 鹏， 高 阳

(1. 上海机电工程研究所，上海 201109； 2. 上海航天技术研究院，上海 201109)

液体晃动问题广泛存在于航空航天领域,关于液体晃动问题国内外学者做了大量的研究[1-8]，这些研究为解决晃动问题提供了基本的解决方案，但是晃动计算理论中的一些假设与实际情况有一定差距，而且理论计算的结果需要试验验证，因此液体晃动模态试验成为研究液体晃动问题的一种重要手段。王立时等[9]对二维容器进行了晃动试验，对液面的自由衰减振动进行了测量及分段稀疏快速傅里叶变换(sparse fast Fourier transform,SFFT)分析，得到了晃动的自然频率和阻尼比，验证了李遇春等[10]的Ritz方法计算精度。王为等[11]采用激光位移传感器测得液体波高的时程曲线，通过对数据的处理，得到晃动频率和阻尼比。李松等[12]通过激光扫描采集液面的速度响应，对速度信号进行快速傅里叶变换(fast Fourier transform,FFT)分析，得到水平放置的半充液圆柱容器的液体晃动低阶频率值。

而对于采用自动驾驶仪的无人驾驶飞行器而言，由于液体晃动频率通常比较低，与飞行器刚体姿态运动频率非常接近，直接针对较低的液体晃动频率设计陷幅滤波器会同时将驾驶仪所需的飞行器刚体姿态运动信号滤除；且在飞行过程中随着燃油消耗，燃油液深变化引起晃动频率时变，导致陷幅滤波器半功率带宽必须足够宽或自适应时变以便覆盖晃动频率变化范围，由此牺牲了驾驶仪的机动快速性控制能力。这给无人驾驶飞行器驾驶仪稳定回路陷幅滤波器设计带来了较大的困难。

为解决当前无人驾驶飞行器工程研制中储箱燃油晃动频率过低且时变，影响驾驶仪滤波器设计的问题，本文设计并加工了极小宽深比的密集“井”型隔板，同时为验证对比效果，配套设计加工常规的竖型稀疏隔板，利用振动台+水平滑台组合进行横向阶跃激励晃动试验，通过激光多普勒非接触测振仪获取储箱燃油液面晃动的速度响应，采用解析模态分解(analytical mode decomposition，AMD) 与希尔伯特变换(Hilbert transform，HT)对两种隔板情况下的液体晃动频率及非线性阻尼进行辨识。试验及辨识结果表明：相比于竖型稀疏隔板，每个被密集“井”型隔板划分形成的极小宽深比区域燃油晃动基频大幅提高，且不会随着燃油液面深度变化而明显变化，晃动阻尼则比竖型稀疏隔板状态下大幅增大，晃动幅度快速衰减，这将有利于无人驾驶飞行器驾驶仪稳定回路陷幅滤波器设计。

1 晃动试验装置及测试方法

分别对安装常规竖型稀疏隔板以及极小宽深比密集“井”型隔板的燃油储箱，利用振动台+水平滑台组合开展了不同充液深度下的晃动试验。不同隔板状态的试验件模型，如图1所示。

图1 试验件模型Fig.1 Test piece models

试验现场及测试照片，如图2所示。燃油储箱试验件材质为透明有机玻璃，长宽与飞行器真实储箱保持一致，高度做到真实油箱高度的1.5倍，防止晃动时液体溢出。试验件固定在水平滑台上，向试验件中注水至相应深度。由于水的透射性很强，激光照射在水上反射效果不好，在水中添加白色染色剂强化激光反射信噪比。Polytec OFV-505激光测振仪固定于液面上方龙门架，调整探头使激光沿静止状态自由液面法向入射。试验过程中，振动台推动水平滑台对试验件施加阶跃激励，激励停止后储箱内液体进入自由衰减晃动，激光测振仪采集自由衰减晃动信号。

图2 试验系统现场照片Fig.2 Photos of test system

2 解析模态分解及希尔伯特变换基本理论

对于液面宽度与液面深度比值较大容器，这种情况下晃动频率一般较低，阻尼比小，衰减慢，是一个以线性晃动衰减为主的过程，以往常见的做法是对振动响应时间历程分段SFFT分析获取频率及阻尼。

但对于在飞行器燃油储箱内添加隔板的情况，此时晃动一般衰减较快，获得的响应数据样本也比较少，且衰减过程带有一定的非线性特征，常规的分段SFFT方法并不完全适用。而基于HT的自由振动分析方法则不受非线性的限制，但该方法只能用于单自由度系统的信号分析，如将其用于多自由度系统，则需要事先对多自由系统的信号进行分解[13-16]。本文采用AMD从自由晃动衰减信号中提取一阶基频信号。

2.1 解析模态分解

设实信号x(t)包含n个频率成分ω1，ω2，…，ωn的单频率成分信号

(1)

则存在若干个二分频率ωbi∈(ωi,ωi+1),i=(1,2,…,n-1)，将x(t)分为两部分

(2)

si(t)=sin(ωbit)H[x(t)cos(ωbit)]-

cos(ωbit)H[x(t)sin(ωbit)]i=1,2,…,n-1

(3)

式中，H[]为Hilbert变换。单频率成分信号可表示为

xi(t)=si(t)-si-1(t)

s0(t)=0

(4)

式中，xi(t)为本征模态信号。

2.2 基于HT的时变系统模态参数辨识

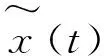
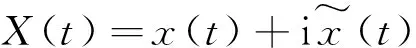
(5)

写成幅值/相位形式

X(t)=A(t)eiψ(t)

(6)

式中：A(t)为瞬态幅值或者包络线；ψ(t)为瞬态相位

(7)

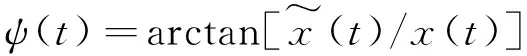
(8)

瞬态幅值及相位对时间t的一阶、二阶导数为

(9)

(10)

(11)

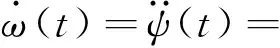
(12)

式中，ω(t)为信号的瞬态圆频率。

解析信号对时间t的一阶、二阶导数为

(13)

(14)

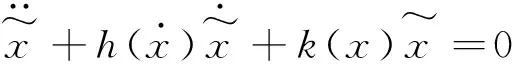
(15)

根据式(5)，可得解析信号的微分方程

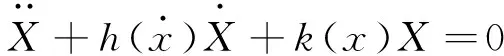
(16)

将解析信号对时间t的一阶、二阶导数代入式(16)得

(17)

对式(17)分离实、虚部得

(18)

(19)

式(18)、式(19)分别为识别出来的非线性阻尼以及刚度表达式。

3 辨识结果

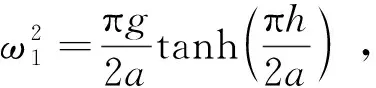
采用AMD及HT分别对燃油储箱试验件中安装常规竖型稀疏隔板以及极小宽深比的密集“井”型隔板状态下的晃动试验结果进行参数辨识处理。不同充液深度情况下的燃油储箱一阶晃动频率，如表1所示。从表1可知，与常规竖型隔板状态相比，加了极小宽深比的密集“井”型隔板后，燃油储箱的一阶晃动频率提升较大，最大可从1.91 Hz提高到6.91 Hz，且不随着液面深度变化而变化。

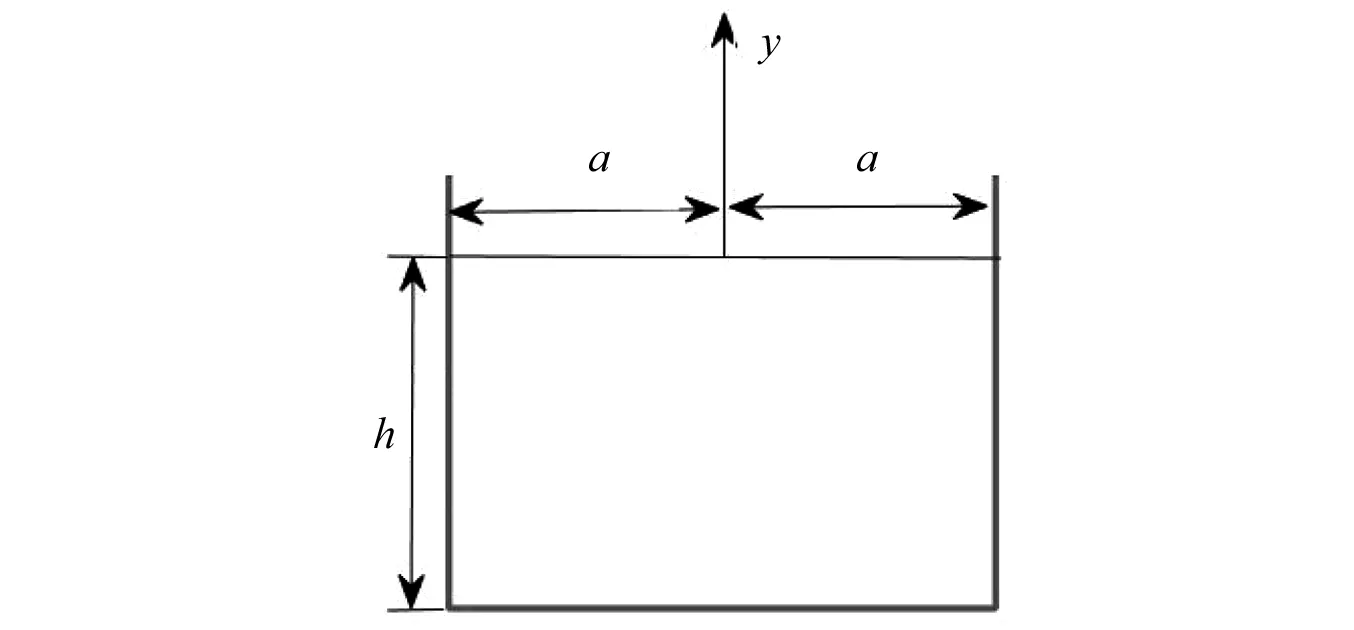
图3 “井”型隔板剖面示意图Fig.3 The profile sketch of “#” baffles

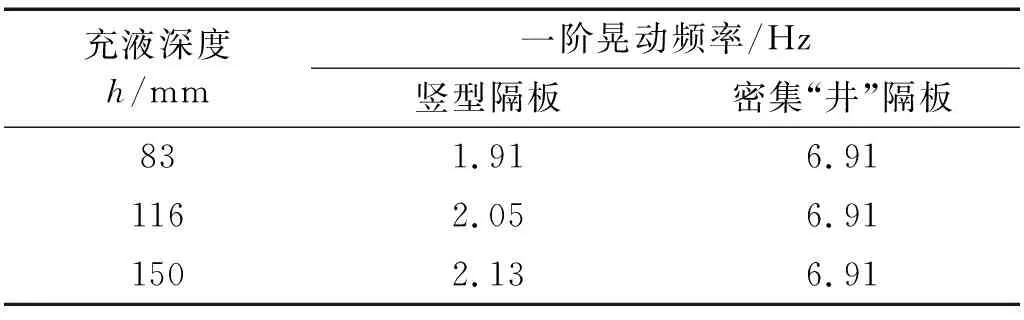
表1 不同充液体深度的燃油储箱一阶晃动频率

对充液深度为150 mm时的试验原始数据进行分析，可得到不同隔板情况下的晃动响应信号包络线、阻尼比随时间变化曲线以及阻尼力-速度曲线，分别如图4～图9所示。从图4、图7可知，与常规竖型隔板相比，安装密集“井”型隔板结构的振动信号衰减特别快，衰减时间约为0.7 s，这也表示安装了密集“井”型隔板后整个系统的阻尼很大。从图5、图8可知，安装常规竖型隔板状态结构的一阶晃动阻尼比基本不会随着时间变化而变化，为0.02左右，而安装密集“井”型隔板结构的一阶晃动阻尼比则随着时间推移而大幅增大，最大甚至达到了0.35。对比图6及图9的阻尼力-速度曲线也可知，安装竖型隔板状态的结构晃动过程中阻尼力-速度曲线是一直线，该直线斜率表征着结构的晃动阻尼，则该过程中结构的晃动阻尼是基本不变的，是一个典型的线性衰减过程；而密集“井”型隔板晃动过程则是一个速度渐小，阻尼渐大的晃动过程，是一个典型的非线性衰减过程。

液体晃动阻尼主要由两部分组成：一部分是液体内部的黏性阻尼；另一部分是液体与容器固壁间附面层摩擦阻尼。一般认为第一部分阻尼要远小于第二部分阻尼，特别是对于低阶晃动阻尼，第一部分贡献的作用比较小，可忽略。在容器中增加隔板来防晃，就是通过增大流体与容器固壁间附面层的面积来增大摩擦阻尼。安装了密集“井”型隔板后，液体在密集隔板表面形成的流体附面层面积大幅增加，液体能量在密集隔板表面边界上的黏性摩擦损耗增大，即液体与密集“井”型隔板间附面层摩擦阻尼大幅增大，衰减加快。

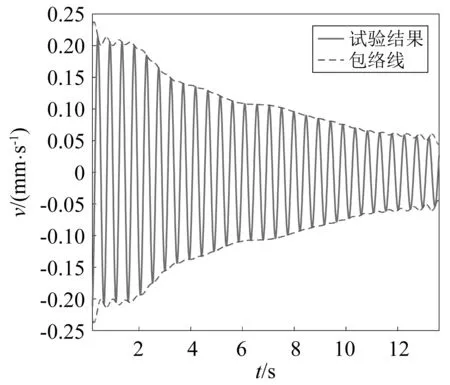
图4 竖型稀疏隔板状态的响应包络线 Fig.4 The response envelop of the fuel tank with sparse baffles

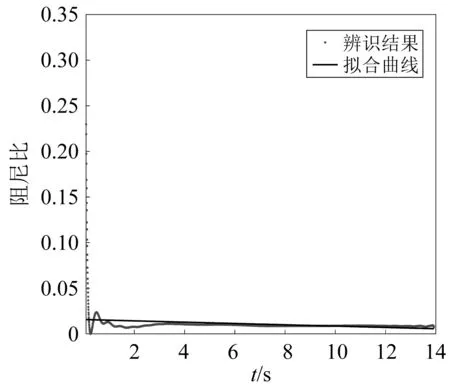
图5 竖型隔板状态的晃动阻尼比曲线Fig.5 The damping ratio curve of the fuel tank with sparse baffles

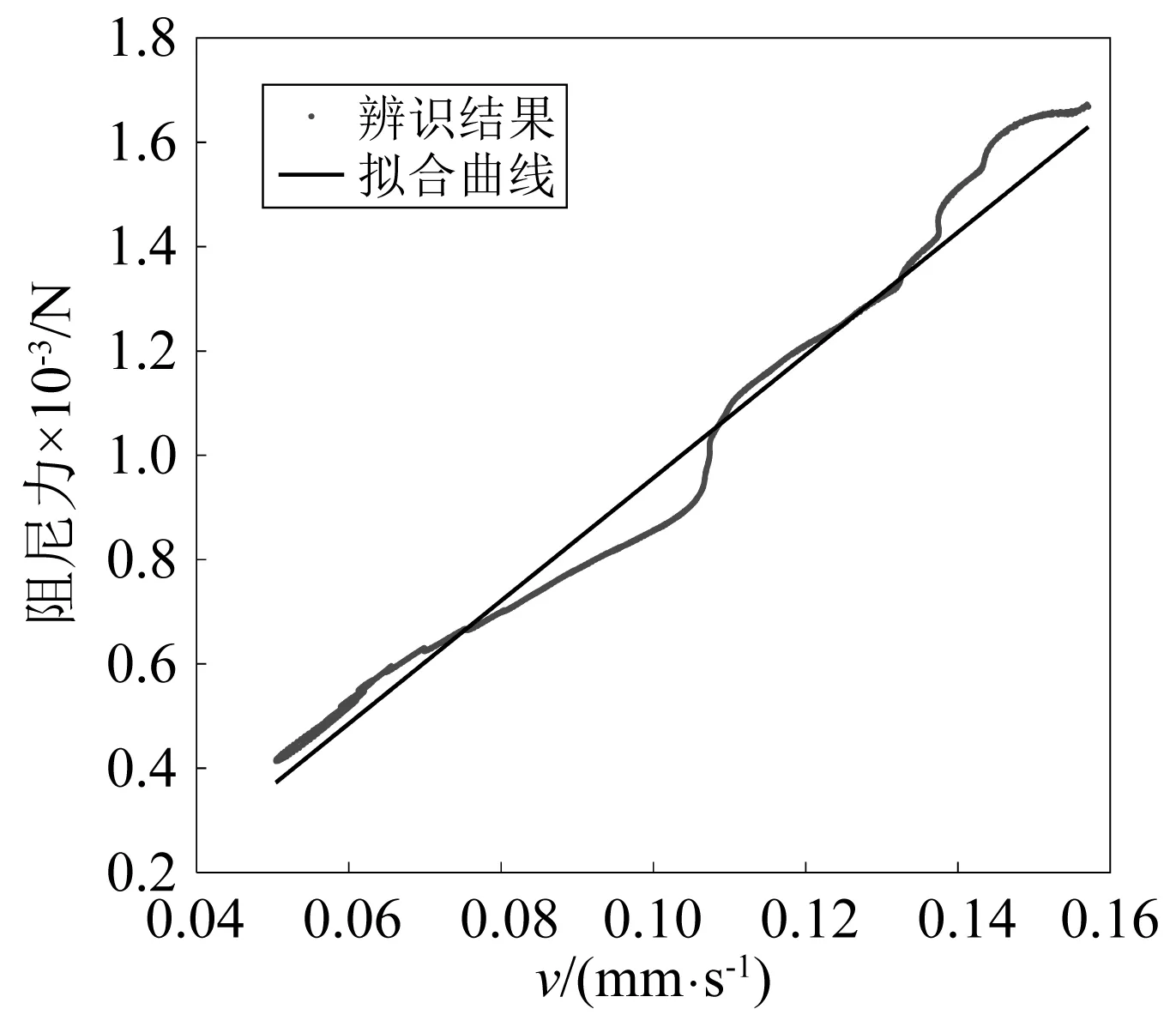
图6 竖型隔板状态的阻尼力-速度曲线 Fig.6 The damping force-velocity curve of the fuel tank with sparse baffles

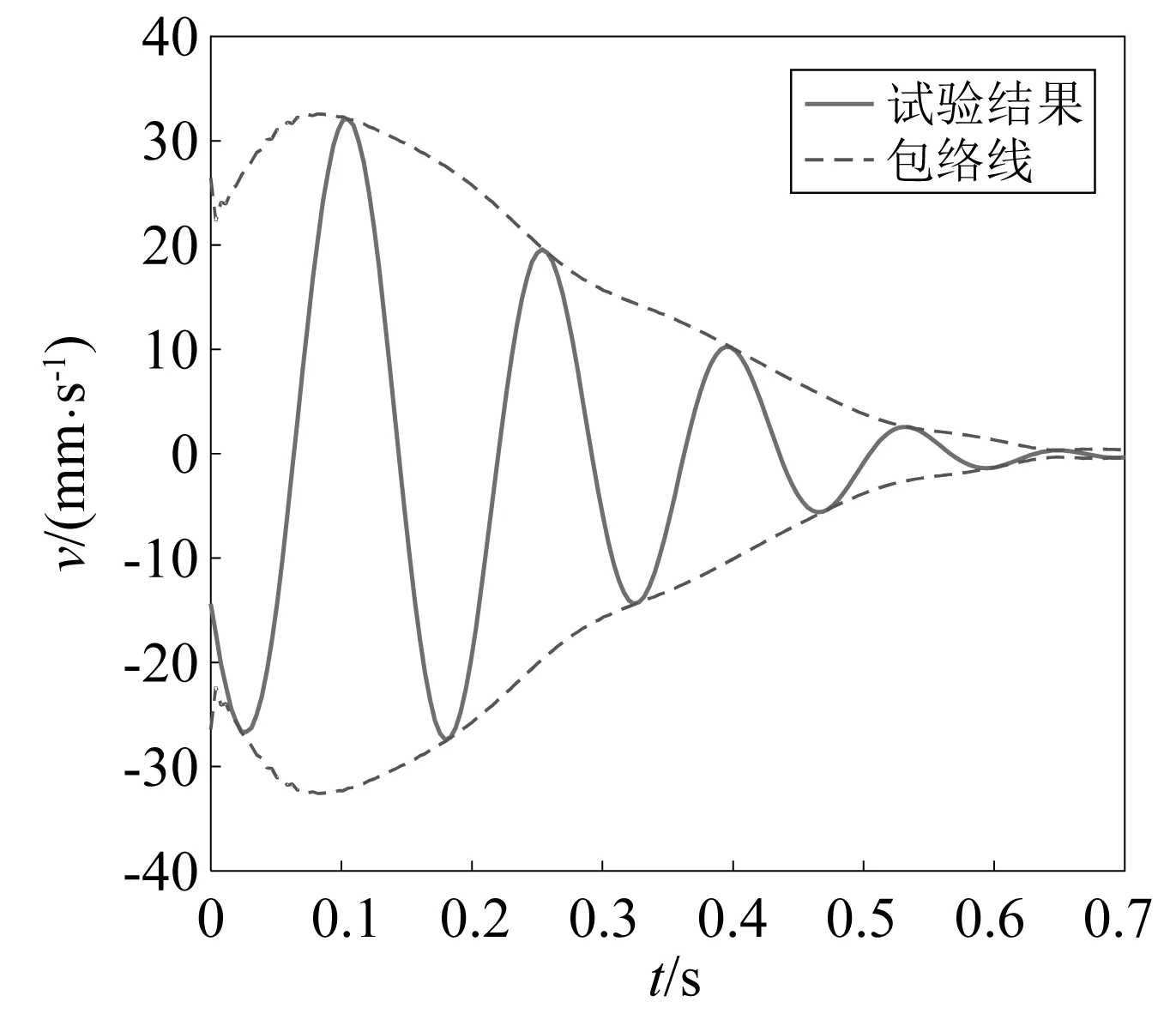
图7 密集“井”型隔板状态的响应包络线Fig.7 The response envelop of the fuel tank with concentrated "#" baffles

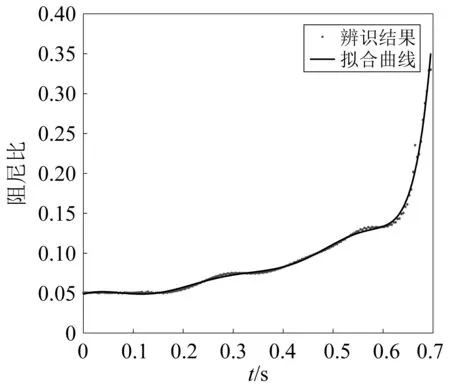
图8 密集“井”型隔板的阻尼比曲线Fig.8 The damping ratio curve of the fuel tank with concentrated "#" baffles

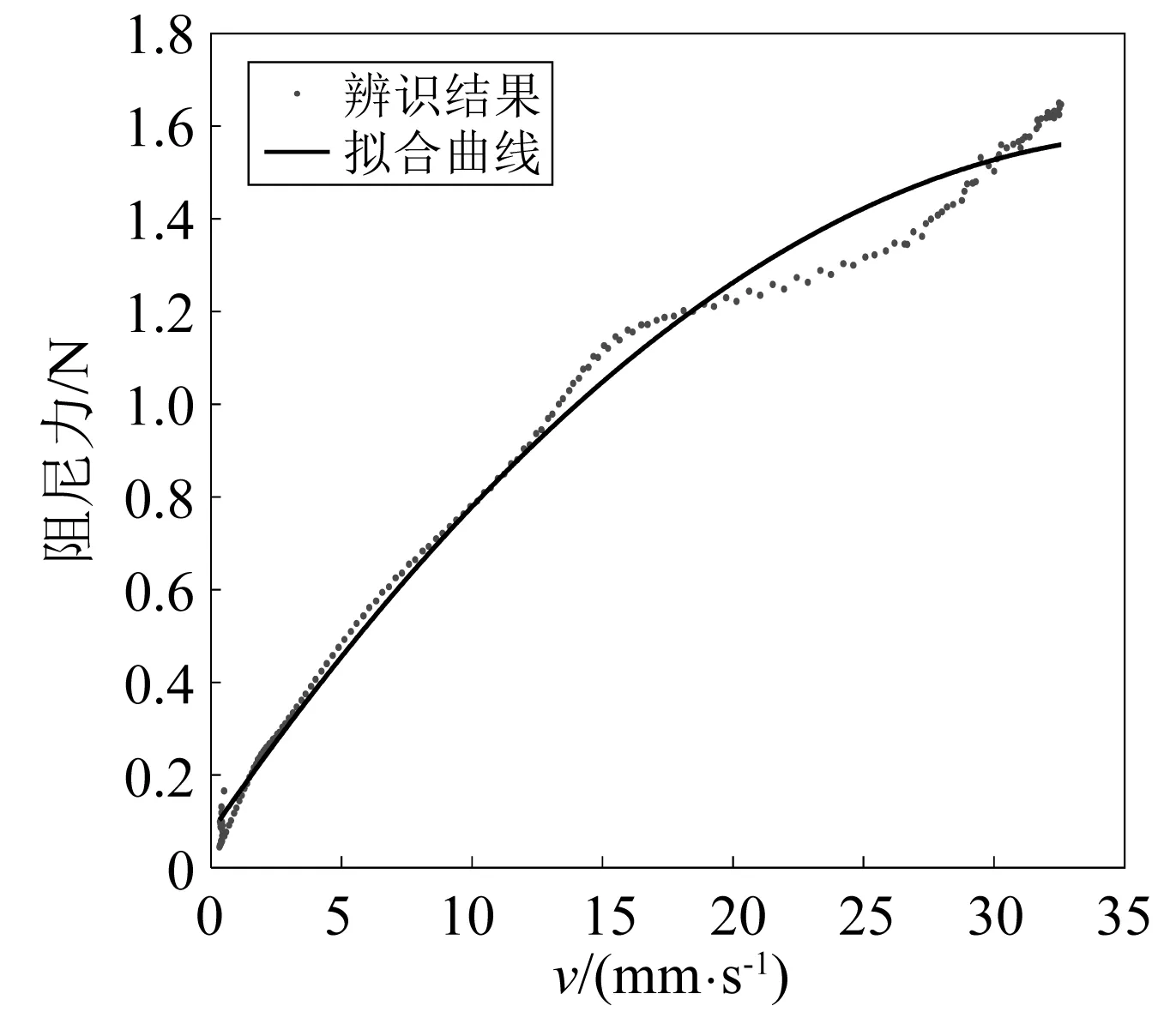
图9 密集“井”型隔板的阻尼力-速度曲线Fig.9 The damping force-velocity curve ofthe fuel tank with concentrated “#” baffles

4 结 论

(1)本文结合解析模态分解及希尔伯特变换，提供了开展液体晃动试验获取液面晃动速度响应，并辨识液体晃动瞬时模态参数的切实可行的试验装置及方法，具有实际工程应用价值。

(2)安装密集“井”型隔板的储箱，其晃动频率大幅提高且不会随着燃油液面深度的变化而变化，同时系统模态阻尼比大幅增大，晃动振幅快速衰减，有益于无人驾驶飞行器驾驶仪稳定回路陷幅滤波器设计。