单轴滚动台车轮多边形磨耗激振试验及动态仿真

刘鹏飞， 杨绍普， 刘永强， 顾晓辉， 刘泽潮， 刘红军

(1. 石家庄铁道大学 省部共建交通工程结构力学行为与系统安全国家重点实验室，石家庄 050043；2. 石家庄铁道大学 机械工程学院，石家庄 050043)

车轮多边形是高速列车中普遍存在的车轮异常磨耗现象，在列车高速行车条件下极易激发剧烈的轮轨冲击振动，严重恶化列车的运行品质。近年来，关于车轮多边形产生机理及其动态影响的研究已受到国内外铁路科研工作者的广泛关注。

在车轮多边形的产生机理及影响因素等方面，朱海燕等[1]通过梳理车轮多边形的研究动态，综合认为轮轴共振、钢轨局部模态、车轮镟修工艺等是多边形产生的主要因素。刘欢等[2]研究指出机车车轮18阶多边形会激发轮对一阶弯曲共振，而牵引力的影响则加剧了机车车轮多边形磨耗的发展。高阳等[3]针对兰新线动车组进行了长期跟踪，认为构架和轮对在320 Hz 及540 Hz 频率附近的耦合共振引起多边形磨耗。肖齐等[4]统计分析了TPDS系统长期监测结果，指出牵引、制动力大的工况下车轮多边形故障占比要更高。Peng等[5]讨论了机车轮对弹性振动的影响，认为轮轨黏滑振动引起的轮轴扭转振动是诱发多边形的一个重要因素。Lan等[6]研究了车轮多边形、货车制动力矩等对车轮磨耗的影响。Wu等[7]通过数值仿真研究了高阶车轮多边形的形成过程，轮对间钢轨的弯曲振动是造成高轮轨接触力的一个主要因素。Fu等[8]研究了车轮多边形的迭代演化仿真模型，并进行了验证。

在车轮多边形的动态影响方面，李彦夫等[9]总结了近年来车轮多边形磨耗与轮轨噪音、振动之间的关系。陈美等[10]针对车轮多边形和钢轨焊缝的复合激励问题进行了研究，指出两种激励不平顺的变化率最大点重合时,引起的轮轨动力作用最剧烈。宋志坤等[11]建立了考虑轮对柔性的高速车辆刚柔耦合动力学模型，确定了1～20阶车轮多边形限值。刘鹏飞等[12]通过现场跟踪测试，研究了重载机车车轮多边形演变规律及其对机车动力学的影响规律。江英杰等[13]通过现场试验测试的方法，研究了出现高阶车轮多边形磨损时车轮通过桥梁、隧道区段时轨道结构的振动情况。Yang等[14]对机车出现的车轮多边形磨耗进行了测量，研究了多边形的演化规律。Liang等[15]研究了车轮多边形激扰下重载机车的轮轨动态接触特性和牵引力的发挥效能。针对现场问题进行了动态测试和解决方案的提出，Johansson[16]对多种车辆进行了车轮不圆顺测试，在动力车轮上存在最明显不圆顺，镟轮会产生初始的车轮表明粗糙度。Fröhling等[17]针对南非机车上出现的多边形问题，认为轮轴扭转振动是主要诱因，并开发了一种振动抑制系统以减缓缺陷的发生。雷晓燕等[18]研究了车轮多边形的动态影响，开展了现场测试，通过锯齿波函数进行了车轮多边形识别。Wu等[19]通过现场调研和试验测试的方法发现轮轨系统激发的550～600 Hz内的模态耦合共振是导致多边形磨耗产生的原因，变速运行可控制其产生与发展。常崇义等[20]利用轮轮滚动接触磨损试验台研究了减缓车轮多边形磨耗的轮轨材料硬度匹配关系，合适的硬度匹配有利于减磨。

相关研究针对车轮多边形磨耗问题从现场测试、数值模拟、动力学仿真分析等角度开展了大量研究，揭示了多变形激扰下的普遍动力学规律和动态影响，也提出了相应的解决方案。利用台架试验进行高阶多边形的高频激振及台架仿真尚涉及较少，鉴于此，本文借助石家庄铁道大学单轴滚振试验台开展了时速300 km/h速度范围内的车轮多边形的室内试验，并针对滚振试验台进行了多自由度动力学建模及多边形激扰仿真分析，从测试和理论分析层面综合研究多边形动态的激扰规律，检验试验台动力学模型适用性。

1 单轴滚振试验台及其动力学模型

如图1所示实尺单轴滚振试验台，总体由轨道轮组、轮对系统、模拟构架、加载反力架及垂向加载作动器组成，其中，加载作动器施加一定数值的静载荷于模拟构架上，由此反映车体载荷的影响，通过电机驱动轨道轮转动并传递切向力至轮对上，从而带动轮对转动获得目标试验速度。在轨道轮上打磨车轮多边形来反映轮轨间的短波不平顺激扰，为了研究多边形的激振效果，在一系弹簧的轴箱处布置了加速度传感器，加速度采样频率5 000 Hz。在多边形激扰下，被试轮对、构架等部件主要做垂向运动。

图1 单轴滚振试验台Fig.1 Single axle rolling vibration test rig

建立了单轮对滚振系统动力学模型如图2所示，模型中考虑构架、轴箱、齿轮箱、轮对和轨道轮结构，均简化为刚体，其中，电机与构架连接于一体。车轮多边形、谐波等激扰以位移激励的形式输入至轮轨接触界面中，轮轨法向接触以经典的Hertz非线性接触弹簧模拟，忽略切向接触力的影响。系统主要参数及取值如表1所示。其中，轴箱质量包括了轴承、轴箱体等质量组成。

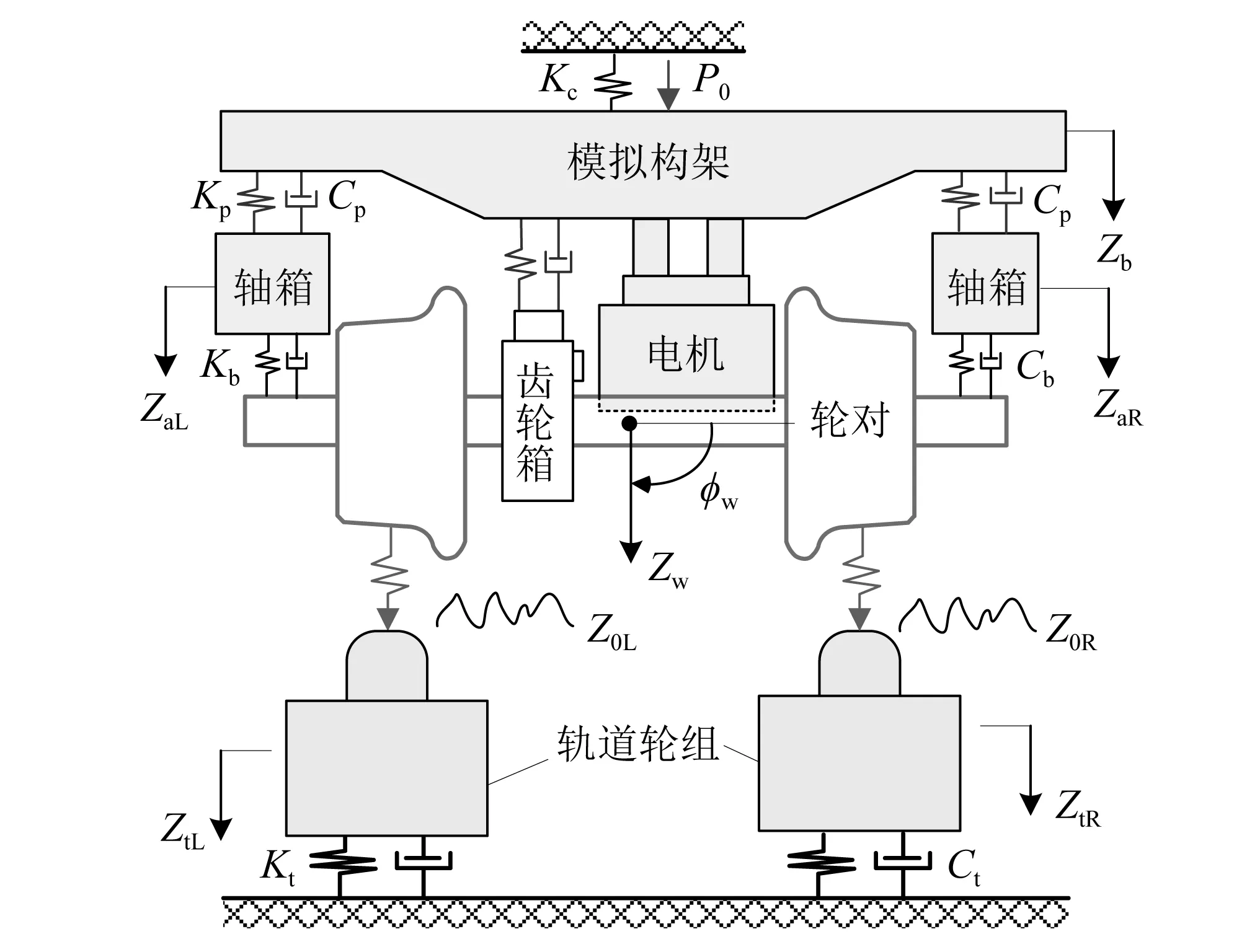
图2 试验台动力学模型Fig.2 Dynamic model of test rig

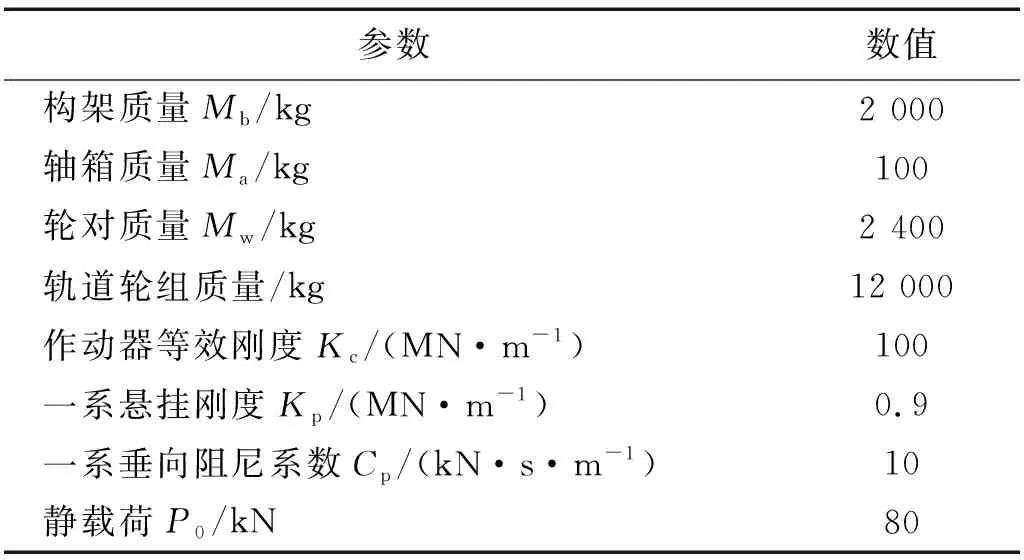
表1 试验台动力学模型主要参数Tab.1 Main parameters of test rig dynamic model

模型中，轴承的支撑刚度kb可按下式计算

(1)

式中：F为轴承上作用的载荷；δ1为轴承的径向弹性位移；δ2为轴承外圈接触变形量；δ3为轴承内圈接触变形量。参照文献[21]，对于高速列车双列圆锥滚子轴承，计算得到的轴承径向刚度为3.87×108N/m，本文直接采用此值作为参数输入。

地面的支承刚度kt计算可参照高速铁路路基刚度，由式(2)得到

kt=EfAt

(2)

式中：Ef为路基的K30模量，根据文献[22]，对于高速铁路路基，其值取190 MPa/mmm；At为单个轨道轮组基座的水平投影面积约为4 m2；即可得到轨道轮下部支承刚度为760 MN/m。相应的阻尼系数Ct取值为5×104N·s/m。

模型中模拟构架、轴箱和轨道轮组的的垂向振动方程分别由式(3)～式(5)给出。

(3)

(4)

(5)

式中，dwk为一系悬挂横向间距之半。

本文关注系统垂向振动，对于轴箱其他方向的振动，将其考虑为与轮对的同步振动。对于轮对和齿轮箱的振动，由于齿轮箱通过抱轴承固定在轮轴上，轮对与齿轮箱除点头运动之外均存在耦合振动，其受力状态如图3所示。图3中，FLx，FRx分别为左、右侧的纵向蠕滑力；FLy，FRy分别为左、右侧的横向蠕滑力，FLz，FRz分别为左、右侧的蠕滑力的垂向分量；NLx，NRx分别为左、右侧轮轨法向力的纵向分量；NLy，NRy分别为左、右侧轮轨法向力的横向分量；NLz，NRz分别为左、右侧轮轨法向力的垂向分量；FxfL，FxfR为一系悬挂纵向力；FyfL，FyfR分别为一系悬挂横向力；FzfL，FzfR为轴承垂向力；MLx，MRx分别为左、右侧的蠕滑力矩在x方向的分量；MLy，MRy分别为左、右侧的蠕滑力矩在y方向的分量；MLz，MRz分别为左、右侧的蠕滑力矩在z方向的分量；Fcx，Fcy，Fcz分别为齿轮箱悬挂力在x，y，z方向的分量。

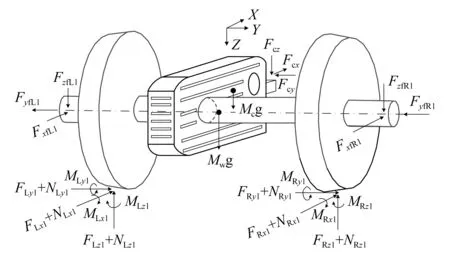
图3 齿轮箱-轮对系统受力状态Fig.3 Force state of gearbox-wheelset system

轮对的纵向、横向、垂向、侧滚、点头及摇头耦合运动方程由式(6)～式(11)给出。

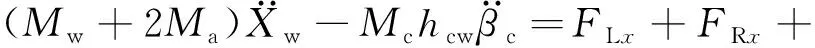
(6)

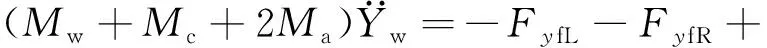
(7)

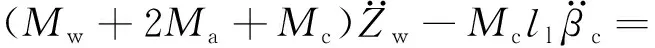
(8)

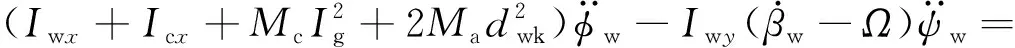
rRi(FRy+NRy)+MLx+MRx+dwk(FzfR-FzfL)+Fcyhdw

(9)

rLψw(FLy+NLy)+MLy+MRy+NLxrL+NRxrR

(10)

(11)

齿轮箱点头运动与轮对垂向、纵向运动存在耦合，其振动方程为

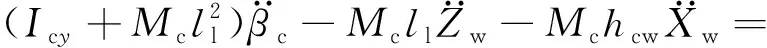
(12)

式中：Mw，Mc分别为轮对和齿轮箱质量；Iwx，Iwy，Iwz为轮对绕x，y，z轴的转动惯量；Icx，Icy，Icz为齿轮箱绕x，y，z轴的转动惯量；rL，rR为左、右侧车轮滚动圆半径；d0为左、右车轮接触点横向间距之半；l1为齿轮箱质心距轮对质心的纵向距离；l2为齿轮箱质心距吊杆的纵向距离；hdw，hcw分别为轮对质心距构架处齿轮箱吊挂点和其质心的垂向距离；lg为齿轮箱与轮对质心的横向距离。

对于轮轨力，轮轮接触点寻迹及切向力的计算可参考文献[23]，法向力N(L,R)采用经典的Hertz接触理论求解，定义轮轨间弹性压缩量为Δz(L,R)，并由此计算轮轨法向动态接触力，分别由式(13)和式(14)给出，其中，Z0(L,R)为左右侧轨道轮不平顺、车轮多边形等轮轨界面激扰输入。

Δz(L,R)=Zw(L,R)-Z0(L,R)

(13)

(14)

式中：G为轮轨接触常数；Zw(L,R)为左右车轮垂向位移。

在振动特性研究中，为获得系统振动的固有频率，需要对模型线性化处理，取轮轨接触刚度为1.6×109N/m，则上述方程组可转化为多自由度系统的固有振动问题进行求解，若忽略阻尼项，方程组变换如下

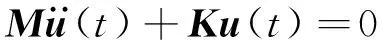
(15)

特征方程

det(K-λM)=0

(16)

式中：M，K分别为广义质量、刚度矩阵；u(t)为广义位移矢量。通过式(16)计算得到的特征值λi(i=1～4)即是系统的固有频率。通过上式算的轨道轮、构架、轮对和轴箱的垂向自振频率依次为42 Hz，50 Hz，184 Hz和345 Hz。

2 车轮多边形台架试验及仿真比较

实际的多边形往往可视为多个谐波的叠加合成，特别是高阶谐波的幅值较小。在试验中，较难重复实际状态下谐波形式的多边形，为此采取了局部打磨的方法，以反映高阶谐波的激扰。根据以往现场测试情况，选取了典型的18阶车轮多边形作为激扰条件，对应的波长为157 mm。同时为方便操作，将打磨点设与轨道轮上，如图4所示。单纯的车轮多边形激振条件下，未施加轨道不平顺，轮轨接触带位于轨道轮顶部，因此打磨点选在接触带，呈离散等距分布状态。轨道轮直径1.8 m，对应的轨道轮多边形为36阶，打磨后实测的轨道轮不圆顺几何状态(见图4)。由于采用人工打磨的方式，各点打磨量较难控制一致，总体的打磨深度在0.5 mm左右。非打磨区维持原轨道轮表面的粗糙度状态。

图4 车轮多边形打磨及其几何形貌Fig.4 Wheelset polygon grinding and its geometry

基于此，开展了100～300 km/h内的多边形高频激振试验和仿真分析。100 km/h速度下测试和计算的时-频域结果比较，如图5所示。从图5可知，轮对低速运行条件下，测试和计算的时域响应具有较好的吻合度，实测结果分布在-40～60 m/s2，数值计算结果在-40～62 m/s2，两者的分布范围十分接近。从频域上看，0.157 m波长激发的基频为176 Hz，仿真结果中，可以明显发现多边形引起的基频的倍频成分，并在轮对振动中占据了较大的能量，这一现象在测试结果中同样存在，在10～1 500 Hz的频率范围内，测试和仿真结果具有较高的吻合度，超过1 500 Hz，测得的轮对振动能量大于计算结果，这与实际结构的弹性振动有关。但总体而言，以刚体模拟的振动台模型已能够较好反映多边形基频和倍频振动。

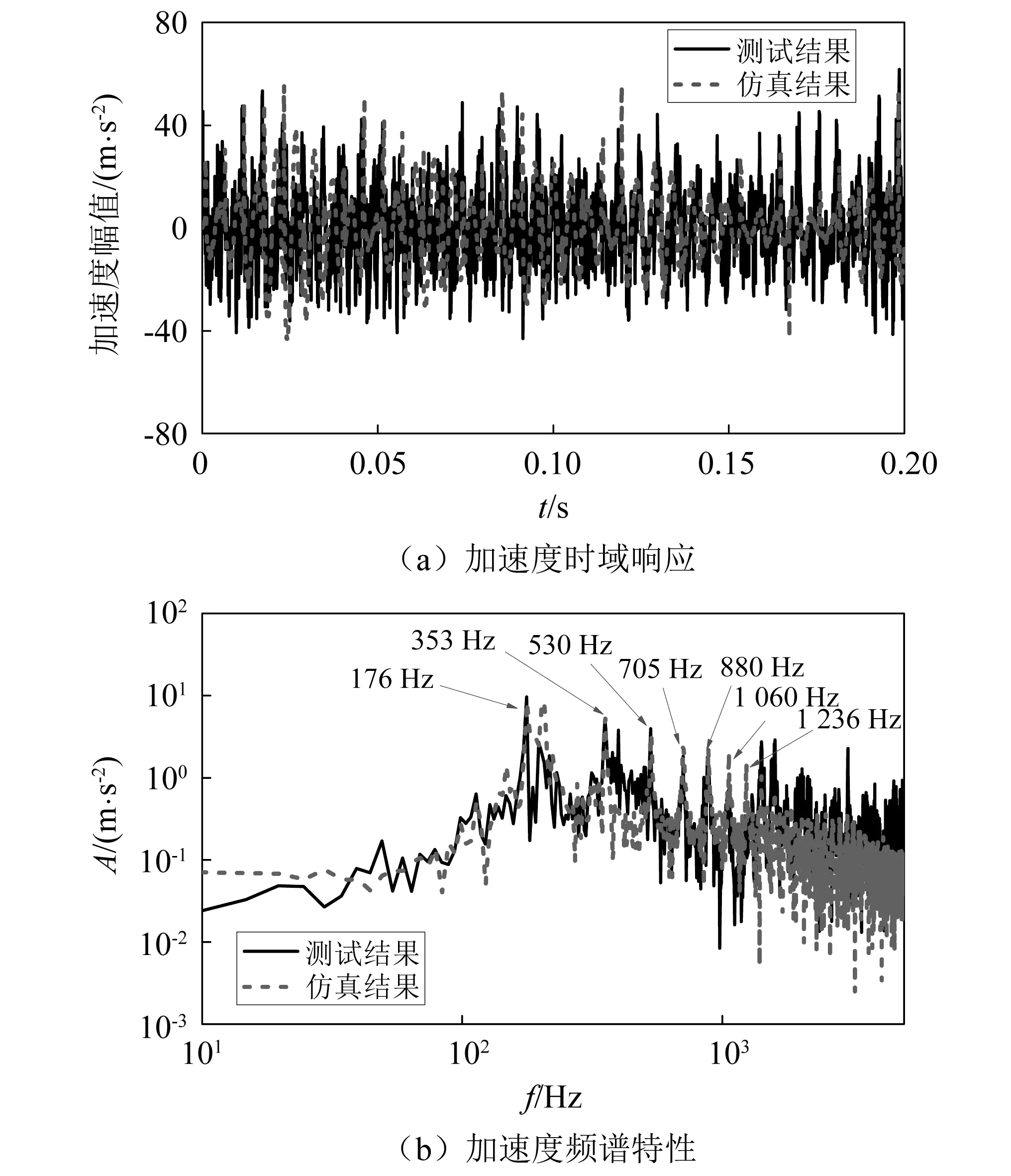
图5 100 km/h速度下测试和仿真结果比较Fig.5 Comparison of test and simulation results (v=100 km/h)

为更方便比较动力学仿真模型对高速条件下轮对振加速度的反映情况，选取加速度绝对值并取其包络曲线进行比较。200 km/h速度运行时测试和仿真结果如图6所示。从图6可知，实测加速度幅值总体是高于仿真结果的，相应的包络曲线差异较为明显。而加速度最大值较为接近，测试和仿真最大加速度分别为97 m/s2和92 m/s2。从频域响应上可以发现，无论是测试还是仿真结果多边形基频(355 Hz)和倍频的激扰提供了主要的振动能量，710 Hz，1 065 Hz，1 421 Hz分别对应了2倍频、3倍频、4倍频振动，且仿真加速度频谱主要反映了强迫振动峰值信息，亦即仿真频谱在峰值上和测试结果呈对齐状态。仿真模型能够较好反映1～4倍频的振动能量，而振动频率高于4倍频对应频率时，振动幅值低于实测结果。

当运行速度增至300 km/h，轮对振动加速度测试、仿真结果的时频特性比较如图7所示。5 000 Hz采样频率得到的测试加速度远高于仿真结果，在频域上体现为多边形激扰的2 500 Hz以上的高频振动高于计算数值，测试和计算的包络曲线波动范围分别为33～117 m/s2和12～73 m/s2，可见加速度的幅值分布具有较大的差异。进一步选用2 500 Hz的低通滤波器对实测加速度数据进行滤波，在图7(a)中可知，时域响应上测试结果的包络曲线波动在13～61 m/s2，相应的仿真结果包络曲线数值在12～71 m/s2，已十分接近，由此也说明理论模型能够较好捕捉多边形激发的2 500 Hz以内的振动信息，在幅值上和振动主频上均得到了较好反映。

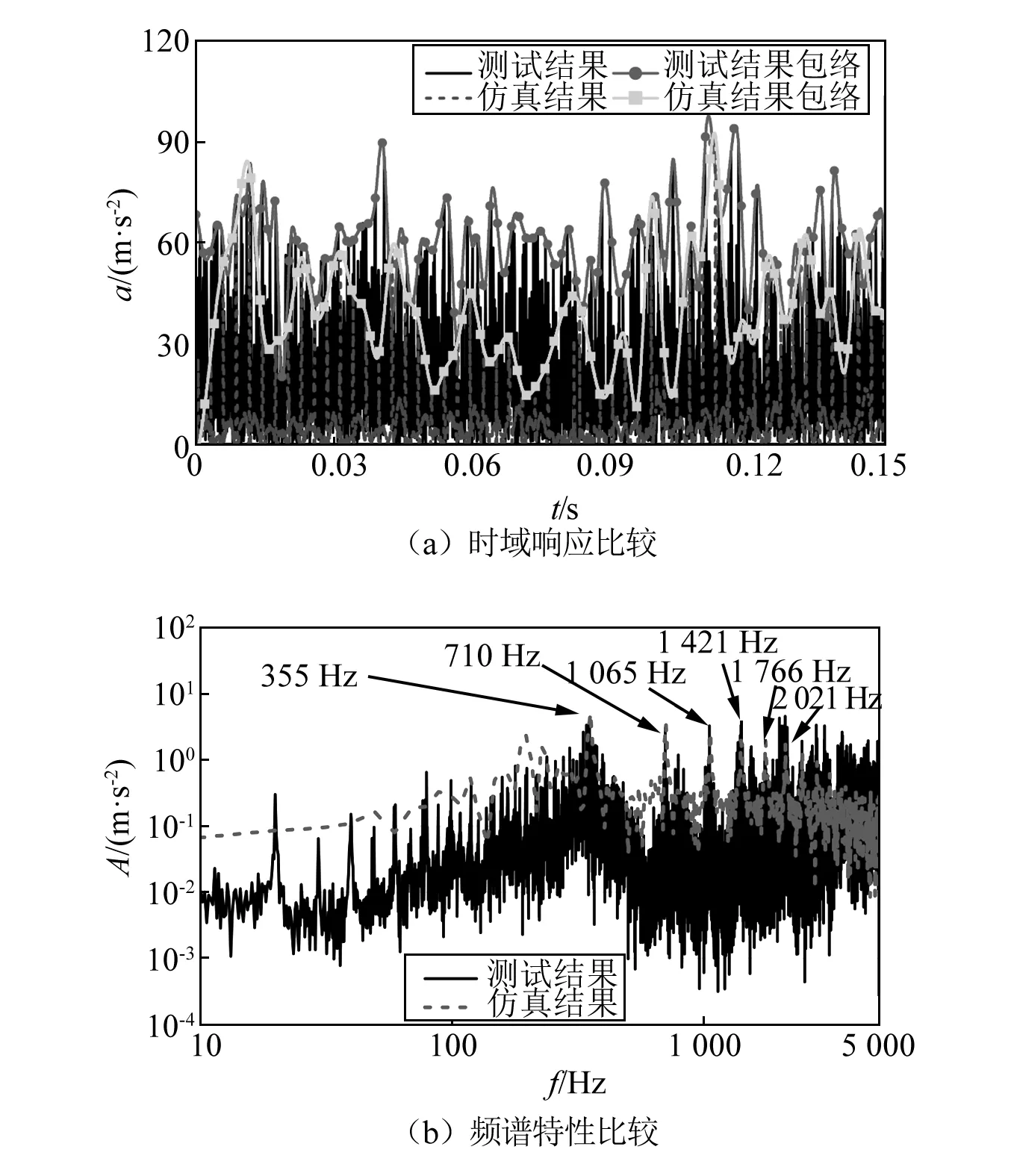
图6 200 km/h速度下测试和仿真结果比较Fig.6 Comparison of test and simulation results (v=200 km/h)

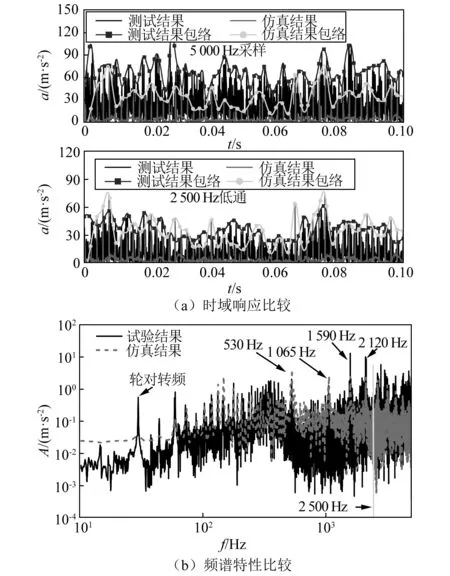
图7 300 km/h速度下测试和仿真结果比较Fig.7 Comparison of test and simulation results (v=300 km/h)

3 单一谐波下轮对滚振试验及仿真比较

轮轨局部凹陷及变形等现象较为常见，在几何上可表述为单一的谐波不平顺，是实际车轮及钢轨上存在是较为典型的谐波型激扰，此外，钢轨的波磨也可视为多个谐波的延拓。针对此工况，进一步开展了50～300 km/h速度范围内的轮对滚振试验，谐波的波长为300 mm，为保证高速运行时的安全性，谐波波深设为0.08 mm。轨道轮谐波外貌、波长波深关系及其极坐标图，如图8所示。轨道轮初始存在一定程度的偏心，而单一谐波可视为轨道轮初始椭圆上的局部叠加。

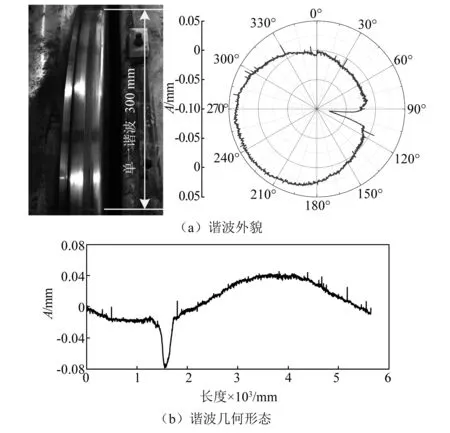
图8 轨道轮单一谐波几何形貌Fig.8 Wheelset single harmonic geometry

为深入研究速度变化对轮对振动带来的影响，首先给出给出低速50 km/h运行速度下轮对轴箱处的加速度时频特性，同时与仿真结果进行了比较，如图9所示。低速条件下轴箱振动幅值在15 m/s2范围内波动，仿真结果也表现出同样的规律，然而，由于运行速度低，单一谐波激发的振动幅度较小，在加速度时域响应中较难辨别。从频域上看，振动能量主要集中在180 Hz左右的轮对振动和350 Hz的轴箱振动主频附近，同样，轨道轮转频2.5 Hz激发的谐波激扰依然量级很小。就测试和仿真结果的吻合度而言，多自由度模型能够较好反映轮对自振，但轴箱的振动特性在频域中体现较弱。而500 Hz以上两种结果也具有较高的吻合度，只是振动能量已不占主导。

在此基础上，给出了200 km/h速度下测试和仿真结果，如图10所示。从图10可知，对于以5 000 Hz采样频率采集的原始数据，仿真与测试结果总体规律上有较好相似度，且能够明显辨别谐波激扰振动响应，从频域上看，实测结果能够反映轨道轮和轮对的转频(分别为10 Hz和19 Hz)，振动能量集中在轮对和轴箱的自振频率附近，转频的倍频振动表现较为突出。测试和仿真结果在1 000 Hz以上的高频振动有较大差别，对实测数据进行1 000 Hz的低通滤波后，仿真和测试结果在动态变化规律和波动幅度上具有较高的重合度，表明多自由度试验台模型对高频振动的捕捉尚有不足。

图9 50 km/h速度下谐波激振结果Fig.9 Harmonic excitation results (v=50 km/h)

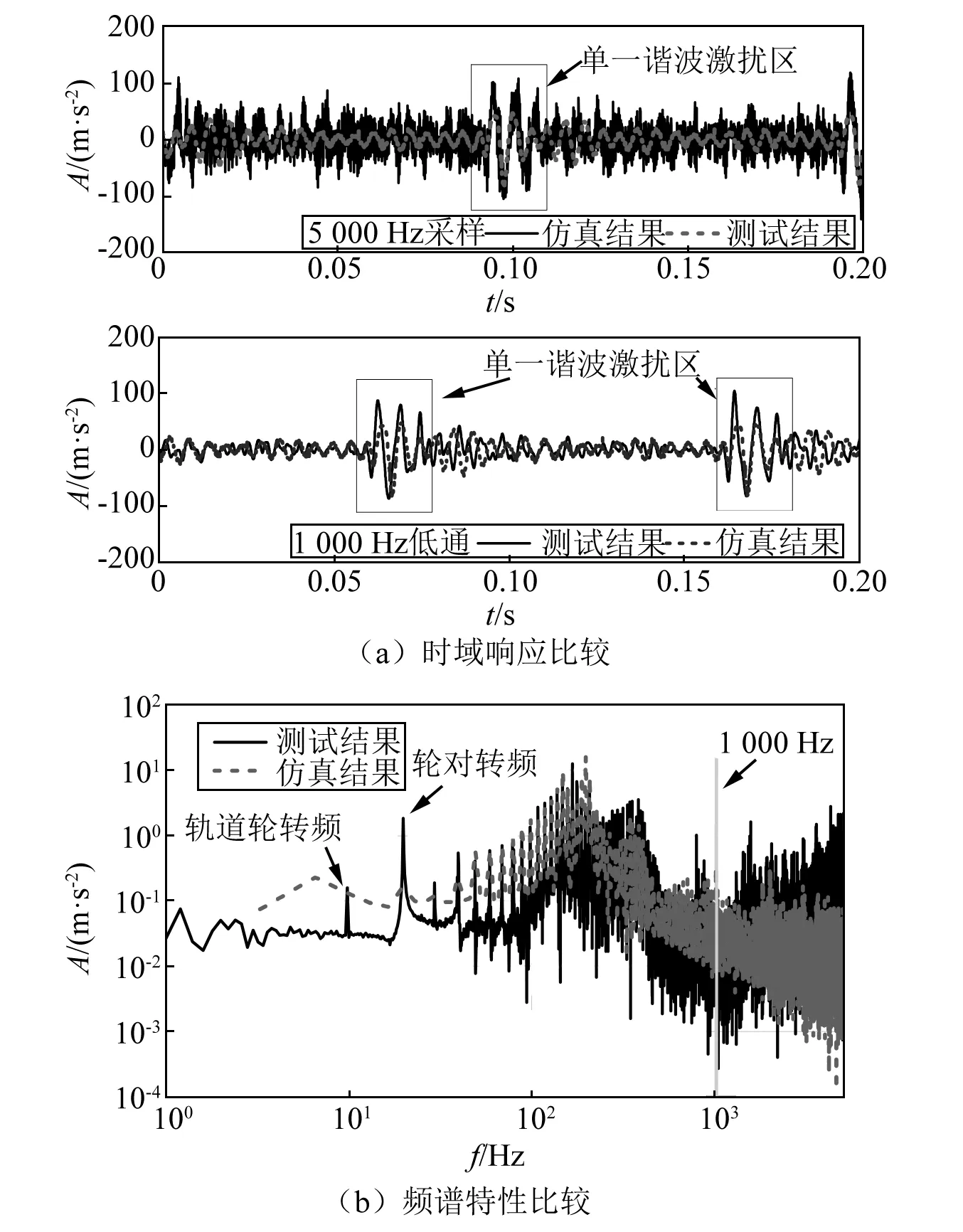
图10 200 km/h速度下谐波激振结果Fig.10 Harmonic excitation results (v=200 km/h)

速度提升至300 km/h，轮对振动加速度的时频特性如图11所示。进入高速运行状态后，谐波激发的轮对振动更为明显，实测最大加速度可达260 m/s2，在频域上，轨道轮、轮对转动引起的振动尤为明显，特别是激发了轮对和轴箱的自振，仿真模型对轨道轮转动、轮对自由振动均能准确反映，但250 Hz以上轴箱自由振动以及更高频率的振动成分要低于实测结果。若对测试数据进行250 Hz低通滤波，两种方法得到的加速度响应和波动幅值十分接近，均在±100 m/s2范围内。

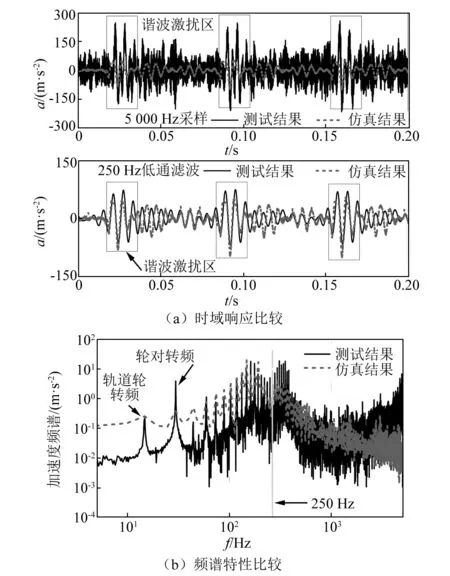
图11 300 km/h速度下谐波激振结果Fig.11 Harmonic excitation results (v=300 km/h)

综合上述分析，对实验台多自由度仿真模型的适用性进行归纳。对于高阶多边形激振工况，仿真模型在200 km/h及以下速度范围内有较好的适用性，能够动态模拟轮对、轴箱等走行部件的振动情况，当速度增至300 km/h时，仿真模型能够较好反映2 500 Hz以下的车轮多边形激发的倍频振动以及轮对系统自振特性。而对于轨道轮单一谐波激扰工况，轮对走行速度在200 km/h以下时，仿真模型总体能够再现1 000 Hz以内的轮对加速度振动幅值和频谱特性，但进一步提速后，轴箱自振加剧，理论模型较难准确捕捉这一特性，模型的有效性限制在了250 Hz以下。

需要指出的是，尽管试验台理论模型采用了刚体动力学假设，但在多边形激振时仍反映出了数千Hz的高频振动，也能再现轮对、轴箱结构等关键走行部件的自振规律。因此，就本试验台而言，基于多刚体动力学的建模方法在较宽的频率范围内仍有其一定的合理性。诚然，对于更高频率振动，该模型尚有不足，结构弹性振动问题是下一步需要予以考虑的。

4 结 论

本文基于单轴滚振试验台，通过在轨道轮上打磨车轮多边形和单一谐波，开展了轮轨系统高频滚振试验，进一步建立了试验台多刚体动力学模型，并以实测轨道轮表面粗糙度作为输入激励，进行了同等工况的仿真研究，重点关注轮对振动行为，得到如下结论：

(1) 通过在轨道轮上打磨多边形，能够激发轮轨系统上千Hz的高频振动，在轴箱振动能量中，多边形激扰的基频及其倍频占据了主导，轮对和轴箱的刚体垂向自振也贡献了较大成分。随着速度的提高，高频振动愈发明显。计算结果总体能够较好反映2 500 Hz以下频率的主频及倍频振动，其时域的幅值特性和频域上的主频分布规律与测试结果已较接近。

(2) 通过轨道轮上设置单一谐波，同样可以激发轮轨系统数百至上千Hz的中高频振动，轮对运行速度增加后，谐波激扰区信号明显加强，高频振动显著。在200 km/h和300 km/h速度条件下，多自由度仿真模型能够较好反映1 000 Hz和250 Hz以下的轮对及振动。

(3) 多刚体动力学常用于描述数十Hz以内的低频振动问题，但就本试验台而言，由于其结构特殊性，该模型在中高频振动分析中同样具有一定的适用性。