一种新的基于LiDAR/IMU组合的室内无人车导航系统
祝瑞辉,蔚保国,李 爽
(1.卫星导航系统与装备技术国家重点实验室,河北 石家庄 050081;2.中国电子科技集团公司第五十四研究所,河北 石家庄 050081)
0 引言
基于惯性测量单元(Inertial Measurement Unit, IMU)和里程计的航位推算系统(Dead Reckoning System, DRS)具有在3D空间中自主导航、连续、易于隐藏等良好特性[1]。但是,陀螺仪固有的漂移误差和加速度计存在的噪声会导致角速度和加速度积分产生累积误差,该误差随运行时间而不断累积,没有边界,这使得DRS在没有其他导航手段辅助的情况下不可靠[2]。外部无线室内定位方法被广泛研究以实现绝对定位,包括伪卫星[3][4]、射频识别(RFID)[5]、近距离通信(NFC)[6]、Wi-Fi[7]、蓝牙[8]、超宽带(UWB)[9]等。所有这些都难以满足UGV对室内定位精度,连续性和鲁棒性的要求。尽管基于外部无线定位设备和惯性传感器研究了多源信息融合技术,包括将Wi-Fi与惯性传感器融合[10][11]、Wi-Fi与蓝牙组合[12]以及Magnetic/Wi-Fi/PDR三者融合[13],仍然无法解决上述问题。
视觉和激光雷达(Light Detection and Ranging, LiDAR)是一种常用的室内定位和构图技术,迭代最近点(Iterative Closest Point,ICP)算法[14]和迭代最近线(Iterative Closest Line,ICL)算法[15]被广泛用于扫描匹配。如果单纯使用激光雷达进行点云的扫描匹配,需要激光雷达有很高的扫描频率,较高的扫描频率会加重计算机CPU的数据处理负担。遗传算法(GA)也是一种原始数据匹配技术,它利用强大的搜索功能在大范围内寻找位姿变化[16]。文献[17]提出了一种由GA和ICP算法组成的混合扫描匹配算法,其中GA用于搜索全局最大值,而ICP算法用于优化从GA导出的初始姿态估计值。然而GA太过复杂,大大加重了服务器的运行负担。当DRS推导的初始姿势估计值与全局估计值相差甚远时,仅使用ICP算法可能会使姿势估计值陷入局部最小值或最大值。本文提出了一种新的2D扫描匹配算法,该算法首先使用遍历搜索估计算法(Ergodic search estimation algorithm, ESSA)来寻找一个大略位姿初始估计值,然后使用数值优化方法对该ESSA估计的位姿进行优化。由谷歌工程师开发的数值优化算法[18]已被有效地证明可以解决具有边界约束的非线性最小二乘问题和实际工程应用中的一般无约束优化问题,已被制图师使用。本文提出的扫描匹配方法的灵感来自hectorslam[19]。但是,我们将适应度函数引入到ESSA中,以在较大范围内搜索良好的初始估计值,而hectorslam在第一阶段使用多分辨率网格图,从不同角度解决了相同的问题。
1 一种新的混合扫描匹配方法
本文提出一种新的混合二维扫面匹配算法,其中遍历搜索估计值算法用于粗略获得姿态变化估计值,然后将粗略姿态估计值作为数据优化算法的初始值,经数值优化后,进一步获得更准确的姿态估计值。
1.1 遍历搜索估计算法
该算法的关键是选择合适的适应度函数来计算每一个候选位置估计准确程度的大小。本文将激光击中占有网格概率之和作为适应度函数来求解位置估计,作为数据优化算法的初始姿态值。算法步骤如下所示。
(1)初始时刻位置。令(x(0),y(0))表示初始位置,t=0表示迭代计数器,T表示最大迭代次数。在初始位置±0.5 m内以0.1 m为分辨率均匀选取M个位置作为初代候选者P(0)。
(2)计算候选者适应度值。由于适应度值的大小决定了它成为最终位置估计值,因此,适应度函数的选择直接影响遗传算法的性能。假设A是一个候选者。令φAi(k)和ρAi(k)分别表示第i个天线的载波相位和伪距观测量,其中k是采样时刻。候选者A的位置表示为PA,第i个天线的位置表示为psati。候选者A的平滑伪距表示为。令RAi(k)为候选者A的预测伪距。载波相位平滑伪距与预测伪距之差为eAi(k);FA(k)为候选者A的适应度值;n是伪卫星天线个数。

算法1:候选者A适应度计算。1. 输入:k采样时刻的载波相位量测φAi(k)。

2. 输出:候选者A的适应度值3. for i=1 : n 4. =φAi(k)×c/fc 5. RAi(k)=||PA-psati||6. eAi(k)=- RAi(k)7. end for 8. FA(k)=
适应度值越小,越接近真实位置值。
(3)终止判定。如果t=T,拥有最小适应度值的候选者被选为最优估计。
1.2 数值优化算法
众所周知,非线性最小二乘问题的成本函数是误差项的总和(称为“残差”)。由遍历搜索估计算法估算的UGV姿态变化表示为,令Tm=[xm,ym,Am]表示量测转换。求解由遍历搜索估计方法计算出的初始位姿估计的旋转和平移成本,该成本随着解与初始位置估计距离的增加而增加。和从扫面帧到映射帧的量测变换Tm之间的加权平移和旋转误差分别计算为[20]:
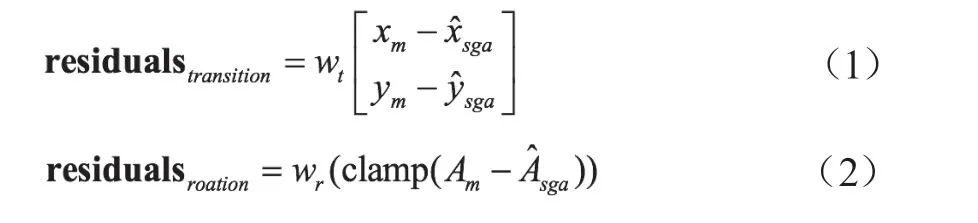
式中,wt和wr分别为平移和旋转的权重。
计算将点云描述的占用空间插入地图的代价,该代价随着可用地图空间将由占用空间代替的数量增加而增加。
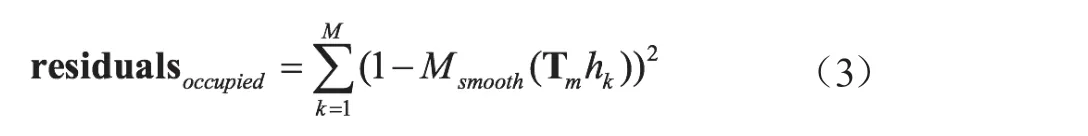
函数Msmooth是映射在图中的概率值的平滑形式,是一个双三次插值函数。由于数值优化算法是局部优化,因此它的精度要高于遍历搜索估计方法,但需要较好的初始估算。获得的扫描点可写为H={hk}k=1,2,…,K,hk∈R2。
2 滤波设计
LiDAR和DRS的紧密耦合仅比松散耦合稍高,但代价是算法更加复杂。本文我们主要想证明所提出系统可以显着降低DRS估计值的累积误差。因此,在提出的系统中,LiDAR与DRS采用松耦合,以降低算法实现的复杂性。将IMU与里程表集成来构建DRS,以获取UGV姿态预测估计。一方面,该预测估计值用作新的混合2D扫描匹配算法运行的初始值,另一方面,它通过UKF与从LiDAR测量中得出的姿态变化估计值进行融合。本文所提系统的框图如图1所示。
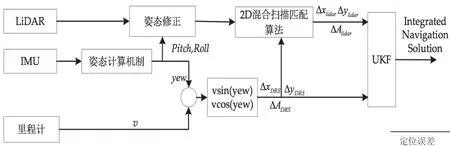
图1 滤波设计
3 试验分析
真实的实验已在测试大楼中使用自行开发的UGV进行,以评估所提出算法的性能。UGV配备了IMU XSENS MTI-10-2A5G4-DK(荷兰),激光扫描仪RPLIDAR A2(SLAMTEC,中国),正交编码器和微型处理器。微处理器用于运行车辆的导航程序,运动控制器模块和电池位于车辆底部,无人车平台由无线控制器控制,IMU、车轮编码器和激光扫描仪的采样频率分别为100 Hz、20 Hz和10 Hz。
图2中的长虚线是UGV行驶的预设参考轨迹,约为190 m。在无线控制器的控制下,车辆从建筑物的东南角开始沿着走廊行驶,然后沿顺时针方向移动一圈后返回起点,在沿着走廊的运动中,无人驾驶车进入教室。图2中的点虚线轨迹是所提出系统的性能。从图2中我们还可以看到,由于手动控制的错误,UGV不能精确地按照当前的参考轨迹运动。例如,当UGV转弯时,实际的运动轨迹是圆弧,而当前的参考轨迹是直角。为了说明所提出算法的有效性,我们忽略了人工运算的错误,这仍然是可行的。
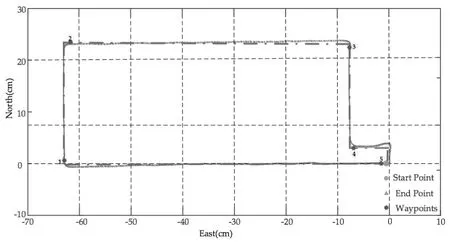
图2 LiDAR/DRS松组合导航轨迹
为了更直观地证明所提出系统的性能,我们选择了5个点作为参考位置(路标),如图2所示。当UGV在测试大楼中行驶时,它停在参考点处以收集至少15 s的位置信息,然后计算位置误差以比较DRS和LiDAR辅助系统的精度。结果如表1所示。在起点处,DRS输出的位置误差为0.45 m,基于hectorslam方法的导航系统为0.14 m,而LiDAR辅助导航系统的位置误差为0.13 m。当UGV移动时,DRS的位置误差继续累积。在终点航路点,DRS的位置误差达到6.30 m,基于hectorslam方法的导航系统达到1.02 m,而由LiDAR辅助的系统为0.48 m,消除了92.4%的误差。
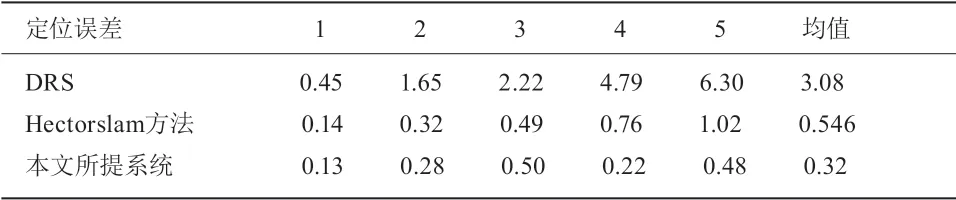
表1 位置误差
姿态角变化曲线如图3所示,从中可以看到,在UGV的整个运动过程中,方位角随UGV的旋转而变化。由于UGV一直在水平面上运动,俯仰角和横滚角几乎为零。
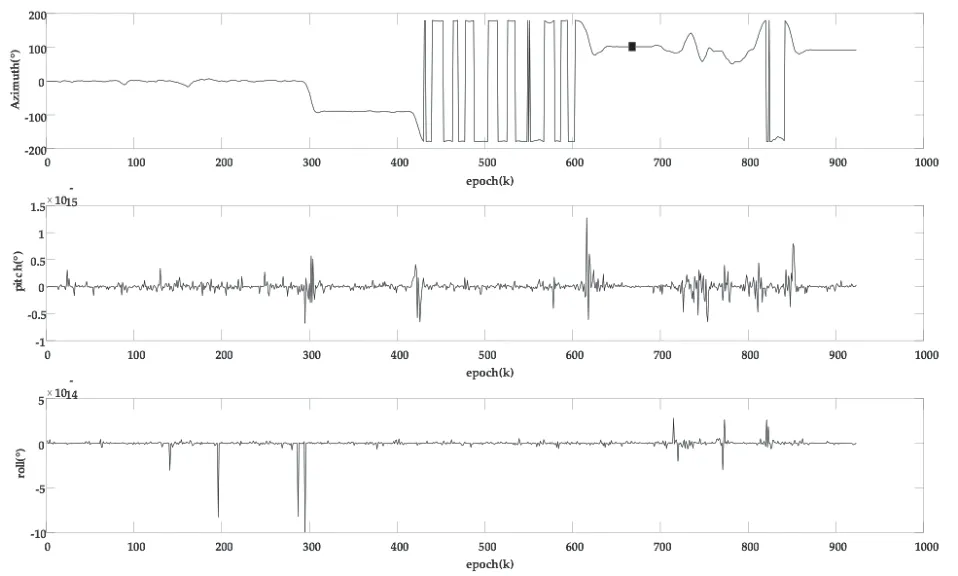
图3 姿态角
4 结束语
在本文中,我们介绍了用于在室内环境中行驶的基于LiDAR/IMU松组合导航系统的UGV平台。DRS由IMU和里程计来构建。此外,提出了一种新的由遍历搜算估计算法和数值优化算法构成的混合二维扫描匹配算法,该算法比基于hectorslam的导航系统更有效。在办公楼的真实实验结果表明,本文提出的系统可以有效减少惯性传感器装置漂移引起的累积误差,提高应用性能,实现了室内办公楼整个轨迹的亚米导航精度。

