耦合Gerdjikov-Ivanov方程高阶孤子解的研究

张毅菲，宋 妮，商慧晶

(中北大学 理学院，山西 太原 030051)

0 引 言

孤立子又被称为孤子(Soliton)，在不受外界阻力影响的理想状态下，其性状基本稳定[1-2]. 目前，对于孤子的精确定义还无法做到统一，但是有关孤子的几个特性却是众所周知的：(1)孤子的能量大多集中在一个狭小的波包中. (2)相互作用后的孤子仍保持原来的速度与振幅属于孤子间的弹性碰撞； 碰撞之后会发生相移，即碰撞后孤子的移动轨迹会发生偏离属于孤子间的非弹性碰撞. (3)同向孤子相互吸引，异向孤子则相互排斥. 孤子动力学性态的研究成果对物理实验和工程实践具有重大意义.

非线性薛定谔(NLS)方程常用来描述Kerr介质中光孤子的传播，NLS方程的可积推广以及高阶干扰项修正是学者们研究的热点. Gerdjikov-Ivanov(GI)方程是NLS方程的一种可积推广，此方程是理论物理中的一个重要模型，在空间凝聚态物理和非线性光学中有广泛应用[3-4]，也称为带导数的非线性薛定谔方程(NLSEIII)[5-6].

(1)

此外，还有两类带导数的NLS方程，分别称为Kaup-Newell方程[7]和Chen-Lee-Liu方程[8]，这三个方程之间存在含有积分的复杂变换，从其他两个方程的性质结论很难得到第三个方程的性质结论，因此这三个方程通常分别进行研究. 已经有很多学者对GI方程进行了研究和讨论，Xu[9]等通过2-重Darboux变换得到GI方程的呼吸解和怪波解； Yilmaz等[10]基于拟行列式的方法也得到GI方程的解. 目前，关于耦合GI方程高阶孤子解间相互作用的研究较少.

本文研究耦合Gerdjikov-Ivanov(cGI)[11-12]方程

|q2|2)2q1=0，

|q2|2)2q2=0

(2)

高阶孤子解的相互作用，其中，q1，q2是与自变量x和t有关的波函数；t是时间变量；x是空间变量.当q1=q2时，方程(2)简化为方程(1). Zhang等[12]通过研究方程(2)的黎曼-希尔伯特问题获得到亮-亮孤子解； Wang等[13]利用广义Darboux变换得到方程(2)的暗-亮孤子； Dong等[14]构造Darboux-dressing变换得到方程(2)的局域波解. 本文利用广义Darboux变换得到cGI方程的二阶孤子和三阶孤子解的迭代表达式，通过数值模拟分析高阶孤子间的相互作用和动力学特性.

1 广义Darboux变换

方程(2)的Lax对为

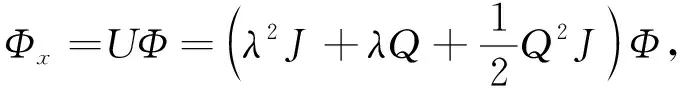
(3)

Φt=VΦ=(2λ4J+2λ3Q+λ2Q2J+λQxJ+

式中：Φ=(φ(x,t),φ(x,t),χ(x,t))T为(x,t)的三维向量函数；λ为光谱参数； T表示向量的转置，星号表示共轭.利用符号计算，方程(2)可由相容性条件Ut-Vx+[U,V]=0得到.

假设种子解q1[0]=q2[0]=0，代入方程(3)得到Lax对方程对应谱参数λ=λ1和λ=λ2的解

(4)

式中：Γ1i和Γ2i(i=1,2,3)是自由参数.

构造Φ2[1]=(φ22[1]φ22[1]χ22[1])T=T[1]Φ2[0]，其中

T[1]为达布矩阵，†表示向量的共轭转置，Φ2[1] 为Lax对方程对应谱参数λ=λ2的解. 根据经典Darboux变换，得到方程(2)的一阶孤子解的表达式

(5)

式中：P11=|φ11[0]|2+|φ11[0]|2+|χ11[0]|2，Q11=|φ11[0]|2+|φ11[0]|2-|χ11[0]|2.

根据上述经典达布变换过程，构造方程(2)的广义达布变换.假设Ψ(λ3+η)=Φ2[1]|λ2=λ3+η是Lax对方程对应谱参数λ2=λ3+η的解，其中η是小参数，利用maple将Ψ(λ3+η)在η=0处泰勒展开

Ψ(λ3+η)=Ψ0+Ψ1η+Ψ2η2+…,

(6)

式中：Ψ0=(φ23[0]φ23[0]χ23[0])T,Ψ1=(φ23[1]φ23[1]χ23[1])T，由于表达式较复杂，这里不再详细给出.定义方程(2)的(N-1)阶广义达布变换(N=2,3)为

(7)

Φ1[1]=(φ24[0]φ24[0]χ24[0])T=Ψ0+T[2]Ψ1,

(8)

q1[N]=q1[N-1]-

q2[N]=q2[N-1]-

(9)

其中

P2(N+1)=|φ2(N+1)[0]|2+|φ2(N+1)[0]|2+

|χ2(N+1)[0]|2,

Q2(N+1)=|φ2(N+1)[0]|2+|φ2(N+1)[0]|2-

|χ2(N+1)[0]|2.

根据以上可知方程(2)的二阶和三阶孤子解的表达式为q1[N]和q2[N](N=2,3).

2 二阶孤子和三阶孤子的动力学特性

基于表达式(9)，在给定谱参数的前提下，对表达式中自由参数Γ1i和Γ2i(i=1,2,3)取值，研究零振幅背景下二阶和三阶孤子的动力学特性.

N=2时，讨论二阶孤子的动力学特性.根据谱参数λ1，λ3的实部和虚部是否相等，分为两种情况：

1) 当Re(λ1)≠Im(λ1), Re(λ3)≠Im(λ3)时，q1和q2具有相同的动力学特性，表现为一个双峰孤子和单峰孤子的弹性碰撞，发生碰撞后两个孤子以原来的振幅和速度继续向前运动，如图 1 所示.

图 1 Γ11=1,Γ12=2,Γ13=3,Γ21=1,Γ22=2,Γ23=3, λ1=0.25+0.25i,λ3=0.5+0.5i的二阶孤子之间的弹性碰撞Fig.1 Evolution diagram of interaction between second-order solitons at Γ11=1,Γ12=2,Γ13=3,Γ21=1,Γ22=2,Γ23=3, λ1=0.25+0.25i,λ3=0.5+0.5i

2) 当Re(λ1)=Im(λ1), Re(λ3)=Im(λ3)时，q1和q2表现为两个双峰孤子发生弹性碰撞，碰撞后孤子的传播轨迹和能量都没有发生改变，在碰撞瞬间能量发生变化，如图 2 所示.

图 2 Γ11=1,Γ12=1,Γ13=1,Γ21=1,Γ22=1,Γ23=2, λ1=0.5+0.5i,λ3=0.4+0.4i的二阶孤子之间相互作用演化图Fig.2 Evolution diagram of interaction between second-order solitons at Γ11=1,Γ12=1,Γ13=1,Γ21=1,Γ22=1,Γ23=2, λ1=0.5+0.5i,λ3=0.4+0.4i

N=3时，讨论三阶孤子的动力学特性，比较谱参数λ1,λ3的实部和虚部，分为两种情况：

1) 当Re(λ1)≠Re(λ3), Im(λ1)=Im(λ3)时，q1和q2都表现为三个孤子间发生弹性碰撞，碰撞前后三个孤子的传播轨迹和振幅都没有发生改变，在碰撞瞬间振幅发生改变，如图 3(a)和图3(b)所示； 保持其他参数不变，调整Г22=3，q1的三个孤子间发生非弹性碰撞，沿t轴，单条孤子的振幅随着时间的变化在减小，相比弹性碰撞，非弹性碰撞瞬间达到的最大振幅变小，能量损失，q1和q2具有相同的动力学特征，这里只展示q1孤子间相互作用演化图，如图 3(c) 所示.在情况(1)的前提下，调换谱参数λ1和λ3的值，q1和q2三个孤子的传播方向发生改变，振幅减小，其他动力学特性与情况(1)相同，如图 4 所示.

图 3 Γ11=1,Γ12=1,Γ13=1,Γ21=1,Γ22=1,Γ23=1,λ1=0.5+0.25i,λ3=1+0.25i的三阶孤子之间相互作用演化图

图 4 Γ11=1,Γ12=1,Γ13=1,Γ21=1,Γ22=1,Γ23=1,λ1=1+0.25i,λ3=0.5+0.25i的三阶孤子之间相互作用演化图Fig.4 Evolution diagram of interaction between third-order solitons at Γ11=1,Γ12=1,Γ13=1,Γ21=1,Γ22=1, Γ23=1,λ1=1+0.25i,λ3=0.5+0.25i

2) 当Re(λ1)=Re(λ3)且Im(λ1)=Im(λ3)时，q1和q2的动力学特性相同，三个孤子有相同的传播方向，传播过程中振幅出现了有规律的振荡，但碰撞前后能量没有发生改变，碰撞瞬间的最大振幅为4，三个孤子之间存在弹性碰撞，如图 5(a) 和图 5(b)所示； 保持其他参数不变，调整Γ22=1.2，一个孤子的振幅由碰撞前的2减小为1，能量发生变化，此时三个孤子间存在非弹性碰撞，这里只展示q1孤子间相互作用演化图，q2与q1类似，如图5(c)所示.

图 5 Γ11=1,Γ12=1,Γ13=1,Γ21=1,Γ22=1,Γ23=1,λ1=1+0.25i,λ3=1+0.5i的三阶孤子之间相互作用演化图

3 结 论

本文利用广义Darboux变换得到cGI方程的二阶和三阶孤子解的表达式，基于数值模拟绘制了二阶和三阶孤子间相互作用演化图，在取定谱参数的前提下，通过改变方程解表达式中自由参数的取值，得到二阶和三阶孤子在传播过程中存在的弹性碰撞和非弹性碰撞两种动力学特性，所得结果进一步丰富了有关cGI方程解的研究.