基于UCT算法改进的Hex棋博弈系统研究

徐志凡，王静文，李 媛

（沈阳工业大学 理学院，沈阳 110870）

0 引 言

博弈是一种对策行为，广泛存在于社会生活的各个方面，而博弈论主要研究博弈行为中最优的对抗策略，协助人们在一定规则内寻找最适合的行为方式，因此在政治、经济、军事、外交等领域可以应用到博弈论。机器博弈是各个领域博弈理论的起源与基础，其作为人工智能领域的一个重要研究方向，不仅是许多人工智能领域的基础，而且被视为最具挑战性的研究方向之一。机器博弈的核心为建立决策与选择决策，建立决策指在给定规则中将所有可采取的策略建成策略集，选择决策指在策略集中选择一个最佳策略。因此，两者成为了机器博弈研究的主要内容。

Hex棋不仅是国际计算机奥林匹克锦标赛的项目，自2016年起也成为中国计算机博弈锦标赛的比赛项目。由于Hex棋规则简单、易懂，但是选择决策至关重要，因此吸引了越来越多的计算机博弈爱好者的关注与研究。

1 Hex棋简介

Hex棋又名六角棋，译作海克斯棋，是一种二人添子类零和游戏。

典型的棋盘由11×11的六边形格子组成，上下两个边界线为红色，左右两个边界线为蓝色，红色（横向）坐标表示范围A-K，蓝色（纵向）坐标表示范围1-11，如图1所示。棋子为红与蓝两种颜色的圆形棋子，对弈双方各执一种颜色棋子。

Hex棋的对弈规则：双方轮流下棋且红方先手，可以将己方棋子下到任意空闲的格子中，同种颜色的棋子相连则认为其相互连接，任意一方将该方颜色的两个边界用相同颜色棋子连接，视为胜利，例如图1中红方获胜。

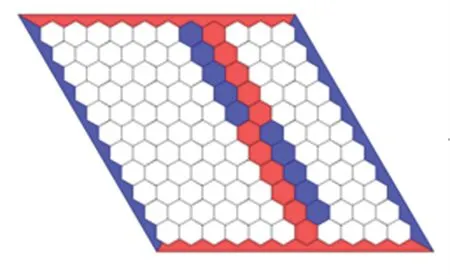
图1 Hex棋棋盘Fig.1 The chess board of Hex

2 Hex棋博弈系统

计算机博弈游戏其核心由搜索和估值两部分组成，传统的搜索方法为Alpha-Beta算法及其诸多变种。由于Hex棋的特殊性，估值算法不能很好的评估当前局面，所以采用UCT搜索算法。该算法能在可控的时间内获取到准确的结果。

2.1 UCT算法

UCT算法（Upper Confidence Bound Apply to Tree）即为上限置信区间算法，是MCTS算法（Monte Carlo Tree Search）的改进。UCB公式（Upper Confidence Bound）最初是针对K臂赌博机问题提出来的，而UCT算法将MCTS搜索与UCB公式相结合，在大规模博弈树的搜索过程中相对于传统的搜索算法在时间和空间方面占据优势。UCT算法的优势在于工作时间可控、具有更好的鲁棒性，并且搜索过程中，博弈树以非对称的形式动态扩展开。UCT算法树内选择的UCB公式（1）：

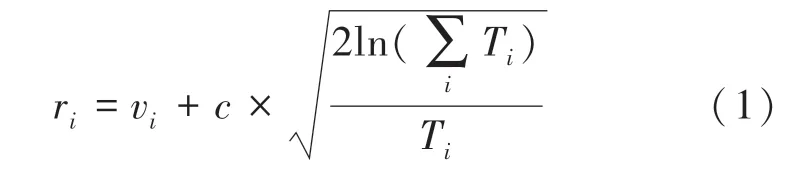
其中，r是树内选择的评估值，选择过程中会根据r选择节点；v是以n为根节点的子树的所有模拟结果的平均值，反映此节点能提供的回报值；T是节点n的访问次数，即此节点被树内选择策略选中的次数；是一个手工设定的参数，用来平衡开发与探索之间的关系。

UCT算法的执行过程，如图2所示。

图2 UCT算法的执行过程Fig.2 UCT algorithm implementation process

UCT算法的执行过程分为4个阶段：

（1）选择阶段：从根节点出发向下探索，选择具有最大值的孩子节点，并将其作为下一次选择的起点，直到到达叶子节点；

（2）扩展阶段：将选中的叶子节点所允许的所有可行下法作为新的叶子节点，加入到搜索树中，并初始化值与值；

（3）模拟阶段：对当前局面进行随机模拟，直到棋局结束，一般情况下己方获胜评估值取1，失败评估值取0，通过若干次模拟后会得到新的值；

（4）反向传播阶段：当叶子节点通过模拟获得新的值和值时，UCT算法通过反向传播更新搜索路径上所有节点的值和值，公式（2）～（3）：

2.2 特殊棋型

Hex棋与许多其他棋类一样，存在着一些特殊棋型，当出现这些棋型时会存在最佳解。

（1）双桥棋型。对角棋子同色且中间为空的棋型即为双桥棋型，如图3所示。无论敌方在中间哪个空位置落子，己方都可以在另一个位置落子来保证己方棋子相连。

图3 双桥棋型Fig.3 Double bridge pattern

（2）无用位置。如果某个位置无论被哪一方的棋子占领均不会对最终结果产生影响，则称该位置为无用位置，如图4所示。

图4 无用位置Fig.4 Useless location

（3）被捕获位置。如果某些空位置填充一方棋子均不会对最终结果产生影响，则称该位置为被捕获位置，如图5所示。

图5 被捕获位置Fig.5 Captured position

（4）边界位置。在边界处会存在一些棋型，无论敌方下在哪个位置，己方都存在另一个位置来保证与边界相连，则称这些位置为边界位置，如图6所示。

图6 边界位置Fig.6 Boundary position

（5）梯子棋型。由于己方局面的某一个位置为迫切相连的位置，而敌方可以行棋在另一位置阻止此相连，并且此时己方仍存在一个迫切相连的位置，最终导致形成梯子形状的棋型称为梯子棋型，如图7所示。

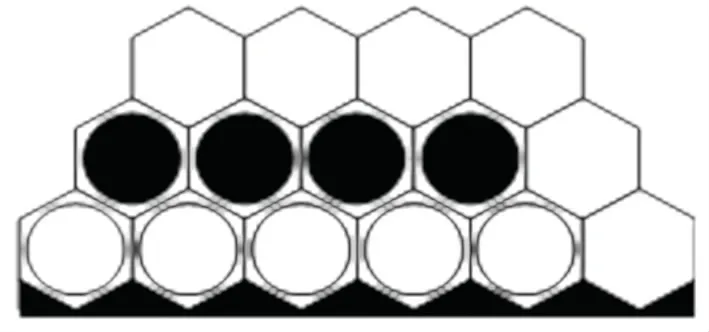
图7 梯子棋型Fig.7 Ladder pattern

2.3 改进的UCT算法

由于在UCT算法的模拟阶段中，一般情况下的模拟是随机选择一种当前局面下的可行下法，判断局面是否获胜，未获胜则继续以上过程，直到胜利2。该方法的模拟用时过长，在一定时间内的模拟次数不理想。由于Hex获胜的特殊性，可以得出一个简单的结论：当棋盘填满时必定有一方获胜。所以采取随机填满棋盘后判断输赢的方法，这会使模拟用时大大缩短。

由于简单随机模拟会使模拟结果与准确结果有较大的误差，依据Hex棋在模拟阶段采用不同棋型对应的最优解可以提高模拟精度的特点，在模拟前采用3种策略：

（1）随机填充双桥。由于双桥自身的特点，无论另一方如何行棋都能保证双桥能够相连，所以在模拟前随机将双桥位置填充，一个己方棋一个敌方棋；

（2）随机填充无用位置与被捕获位置。由于无用位置与被捕获位置填上相应的棋子不会影响最终的结果，所以在模拟前填上可以提高模拟精度；

（3）破坏敌方双桥。如果在上一个节点己方棋子填充敌方双桥的一个位置，且敌方并未连接其双桥，那么己方棋子自动填充另一位置，破坏敌方双桥。

在模拟时采用3种策略：

（1）自动连接双桥。若一方入侵另一方的双桥棋型，则另一方自动补全双桥，保证棋子相连，防止被对面攻占；

（2）自动连接边界。如果存在边界棋型且敌方入侵该棋型，那么己方会自动填充相应的棋子来保证己方与边界相连接；

（3）自动连接梯子。由于梯子棋型的特点，有时会使己方优势逐渐消失，为避免对己方不利的情况，当己方填充梯子棋型中的相应位置时，敌方棋子自动填充另外一个棋子。按此方法则对己方不利的梯子棋型不会出现，能够提高模拟准确度。

3 实验与结果

3.1 实验环境

测试棋盘为11×11，规定实验测试时单方限时30 min，单步限时30 s。实验仿真环境：Window 10操作系统，Code：：Bloacks；测试硬件环境：Inter（R）Core（TM）i7-8700，主频3.20 GHz，内存为8G，显卡NVIDIA GeForce GTX 1050Ti，六核十二线程。

3.2 选取c值

由于UCT算法中的参数是一个预先设定方参数，所以需要对值进行优化选取。由于Alpha-Beta算法的稳定性，故采用UCT算法与搜索层数为3层的Alpha-Beta算法进行测试，不同值均测试200次，先手后手各100次。优化结果，如图8所示。由优化图可以得出最优的值为0.61。

图8 UCT算法c值优化图Fig.8 UCT algorithm c value optimization diagram

3.3 实验结果

选取搜索层数为两层的Alpha-Beta算法与改进后的UCT算法进行测试，测试结果见表1。

表1 改进UCT-Alpha-Beta对弈结果Tab.1 Result of improved UCT vs Alpha-Beta

由表1可知，改进的UCT算法几乎完胜两层的Alpha-Beta算法，验证了改进UCT算法的优越性。

选取改进的UCT算法与原始的UCT算法对比。测试结果见表2。

表2 改进UCT-原始UCT对弈结果Tab.2 Result of improved UCT vs UCT

由表2可知，改进的UCT算法对弈原始的UCT算法无论先后手胜率都超过了90%，说明结合Hex棋棋型策略改进的UCT算法具有更高的模拟准确度和更高的胜率。

4 结束语

本文针对Hex棋在UCT算法中所得结果准确度不够精确的问题，提出了一种结合Hex棋棋型策略改进的UCT算法。该算法对模拟过程采取了一系列的棋型策略，使得UCT模拟阶段的模拟准确度大幅提升，有效的提高了Hex棋的搜索效率与博弈水平。以此算法开发的Hex棋博弈程序获得了2021年全国大学生计算机博弈大赛Hex棋项目一等奖。虽然改进的算法的博弈水平有所提升，但还存在不够精准的问题，因此结合神经网络，进行强化学习等成为下一步的研究方向。