深度果蝇神经网络及其实时能见度预测

肖应慧，张著洪

（1贵州大学 大数据与信息工程学院；2贵州大学 贵州省系统优化与科学计算特色重点实验室，贵阳 550025）

0 引 言

大气能见度被定义为视力正常的人在白天以靠近地平线的天空为背景，观测黑色物体时易识别和辨认的最长距离。能见度的变化取决于大气的透明度，不良天气现象会导致大气浑浊，使大气透明度降低，特别在诸如雾、雨或空气污染等恶劣天气条件下，能见度较低。近年来，由雾造成低能见度而导致交通事故频繁发生，因此准确、高效地对雾天能见度进行实时预测尤为重要。目前，能见度预测的研究方法主要有应用统计分析法和深度学习法。统计分析法通常有物理建模法和非参数建模法，其经由图像构建物理或数据驱动的概率模型，估计不同雾范围下的大气能见度。物理模型法是基于视觉分析的光反射、折射等物理现象，以及基于Koschmieder定理，建立光传播物理模型，进而利用消光系数实时估计能见度，能见度估计的准确率高低很大程度上依赖于原始图像和无雾参考图像的相似程度；非参数建模法考虑了低能见度情况下图像退化对图像分类的影响。研究表明，能见度可由雾的空间特征进行表征。例如，Nnolim将全局对比度算子与基于分阶的多尺度滤波器结合，将熵和标准偏差融合，对图像进行去雾和图像增强，获得多尺度融合去雾算法，但该算法虽能提升对雾天能见度估计的精度，但不能实时预测能见度。深度学习因能对雾天能见度时序数据在线处理，能捕获数据的中长期依赖关系，已受到广泛关注，并在诸如气象预报等能见度预测中已得到初步应用。例如，Selvaraj等以最高温度、最低温度、最高相对湿度、最小相对湿度和风速增强长为输入量，利用长短时记忆神经网络预测降雨量；Akmaljon等借助快速傅里叶变换（FFT）滤波器去除输入图像的低层次特征，并对每个输入应用频谱滤波器来提取低对比度区域，进而利用三流集成卷积神经网络获得能见度深度学习模型。

综上，现有能见度预测方法主要集中于如何从输入图像中获取有价值的能见度特征。相对而言，深度学习法比统计分析法在能见度预测中更有应用前景，但因网络结构复杂、计算效率低、易于出现过饱和或欠拟合现象，使得其应用于能见度的研究有待深入开展。为此，本文在已获针对碰撞检测的果蝇前馈神经网络基础上，从果蝇视觉感知和学习的行为特性出发，尝试性提出一种深度果蝇神经网络（Deep Fly Neural Network，DFNN），并应用于实时能见度预测。

1 果蝇神经信息处理

果蝇有两只复眼，每只复眼由大约3500个小眼组成，且每个小眼包含8个光感受器。光信息通过复眼进入果蝇的视觉系统，实现光传递。果蝇视觉系统具有独特和简单的眼结构，对外界环境信息的感知能力强，其神经系统依次经由光感受器（Photorceptor）、视网膜（Retina）、薄膜层（Lamina）、髓质（Medulla）、小叶（Lobula）及大脑神经信息处理层，执行视觉信息的处理和传递，各层之间分工明确又联系紧密，如图1所示。

图1 果蝇视觉信息处理的流程图Fig.1 Flow chart of visual information processing in fly

光感受器层（Photorceptor）主要由感光细胞组成，负责接收外来的光强度信息；视网膜层（Retina）接收光感受器层输出的信号，负责消除视觉噪声信号；薄膜层又称为视叶神经层（Lamina），包含墨盒cartridge（cart）和开关on-off（oo）这两种类型节点，其中cart节点接收来自视网膜上对应节点的邻域节点的输入，并通过卷积滤波产生输出信号，而oo节点负责接收对应cart节点邻域内节点的输出信号，并经由超极化和去极化处理，产生行为输出量；髓质层包含柱状神经元和切向细胞，由主通道子单元的两类结点（、）组成，其中节点接收薄膜层中对应的oo节点的输出，并输出检测节点处的局部方向；节点接收节点邻域处的局部方向量，经由投影产生在水平、竖直方向的方向量；小叶层汇集髓质层中所有节点的水平、竖直方向量，并将信息整合后输入果蝇大脑神经系统。最后，大脑神经通过接收小叶层的信息以及神经元相互作用机制，获得视觉信息刺激后的反馈信号，并将误差信号反馈入光感受器层。

2 深度果蝇神经网络

基于果蝇视觉系统的信息处理机制，针对视觉场景下的碰撞检测与预警问题，获得一种人工果蝇视觉神经网络（Artificial Fly Visual Neural Network，AFVNN），其由4个神经层构成。在此，对该神经网络作适当改进，得到用于实时能见度预测的改进型深度果蝇神经网络（Deep Fly Neural Network，DFNN）。DFNN由提取图像特征的视觉神经网络和多层感知器（Multiple Layer Preceptor，MLP）构成前向传播神经网络，经由梯度下降更新网络中卷积参数、权值和阈值，实现误差反向传播。改进型果蝇深度神经网络结构如图2所示。

图2 果蝇深度前馈神经网络的示意图Fig.2 Schematic diagram of the Fly deep feedforward neural network

给定由时间序列灰度图与标签构成的训练集｛（A，Y）｝，A为第时刻的灰度图，Y为维的标签或观测值向量。经由图2获知，DFNN接收连续的视频图像帧，并依次经由视网膜、薄膜层、髓质层这3个视觉神经层提取输入图像的特征信息，进而经由MLP产生神经网络的输出信号。

2.1 前馈传播

2.1.1 Retina层

该层由个Retina节点形成的行和列矩阵表示，在第时刻接收灰度图像A，在此3（2），3（2）。Retina节点（，）在第时刻接收输入图像中对应像素点处的灰度值L（）（光亮强度），并经由式（1）输出光亮强度偏差信号：

其中，（）表示时滞函数。

2.1.2 Lamina层

此层由cartridge和on-off两个子层构成。cartridge层由（2）（2）个cart节点构成，依据窗口大小为3×3、步长为1的滑动方式，每个节点接收对应的3×3个Retina节点的输出，并经由高斯滤波器产生该节点的输出膜电位，即式（2）：

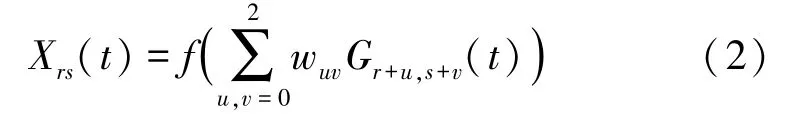
其中，1≤≤2；1≤≤2；w是待定的33权重矩阵中位置（，）处的元素；（）是非线性激活函数。类似地，on-off层由（2）（2）个oo节点构成，其依据扩边方式和窗口大小为3×3、步长为1的滑动方式，每个节点接收对应的3×3个cart节点的输出，并经由如下侧抑制机制，输出其膜电位，式（3）：

在此，E（）是cartridge层中节点（，）输出的膜电位的偏差量，即式（4）：

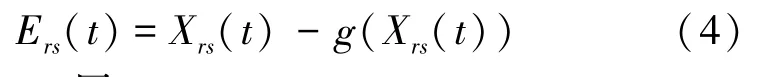
2.1.3 Medulla层

此层由个m节点按矩阵排列表示，其中（2）3，（2）3。首先，将Lamina层中按矩阵排列的（2）（2）个oo节点划分为个子块。基于对称EMD运动方向检测器和3×3权值矩阵，m节点（，）经由式（5）输出膜电位：

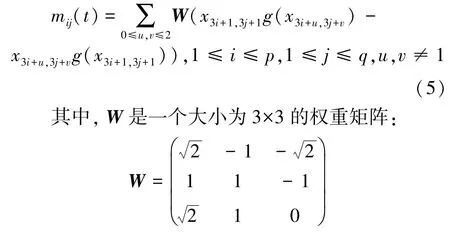
2.1.4 全连接层

其中，为Lamina层中权重矩阵；与分别是MLP中连接权值和阈值构成的矩阵；Y（）为标签值；为一个训练周期的批量大小。

2.2 反向传播

由式（8）可知，FVNN的反向传播是将前馈传播的误差量反向传递给各神经层，并更新全连接层中的权值、阈值和Lamina层的权值。Lamina层的权值由式（9）更新：

其中，是给定的学习率。全连接层的权值与阈值经由式（10）～（11）更新：

其中，∈（0，1），学习率（）依据前馈误差作自适应调节，即式（12）：

其中，k和k为增量和减量因子。

2.3 DFNN的算法描述

结合以上各层的设计，DFNN的算法描述如下：

（1）参数设置：灰度图大小；学习率；参数k和k；

（2）置←，，，随机初始化、及；

（3）输入第时刻的样例（A，Y）；

（4）依据式（8）计算前馈误差值；

（5）经由式（9）～式（11）更新网络中的权值和阈值，并输出第t+1时刻的能见度预测值；

（6）←1；若不满足终止条件，则返回（3）；否则，则结束。

DFNN的算法计算复杂度主要由步4～5确定。在一个迭代周期内，Retina和Lamina层分别进行2和20（224）次运算；Medulla层共进行（13262652）3次运算；全连接层共运算2（2222）9次。另一方面，在反向传播中，全连接层共进行（36666）9次信息传播操作；Medulla层共进行（10202040）9次乘除法运算；Lamina层共进行9（82164164409）9次运算。因此，DFNN在一个时间周期内，前向传播的计算总次数为

由此可知，DFNN的计算复杂度主要由输入图像分辨率、和确定；因此，只要适当设置、和的取值，DFNN的运行效率能得到保障。

3 数值实验

在Windows10（CPU／i34170 3.70 GHz，RAM／4 GB）／Python 3.6环境下展开数值实验。为验证神经网络DFNN应用于能见度预测问题的有效性，选择经典的卷积神经网络CNN、多层感知器MLP以及改进型的VisNet参与比较。各算法的最大迭代次数均为1858。经参数调试，DFNN的参数设置为k＝2，k＝05，4，001，01；CNN的卷积层和池化层的层数均为5，隐含层数5；CNN与MLP网络的激活函数为和一元线性函数（），学习率为0.01；VisNet的参数设置源于相应的文献。

3.1 模型指标

为评估模型的性能，各模型的输出和预测值时间序列均利用已有的均方根误差（Root Mean Square Error，）、平均绝对误差（Mean Absolute Error，）、平均绝对百分比误差（Mean Absolute Percentage Error，）、决定系数（Coefficient of Determination，）以及准确率（Accuracy，）进行模型评价。作为一种绝对误差度量指标，刻画模型的离散程度，该值越接近0，则模型的稳定性越好；度量模型的预测能力，其值越小，则模型的预测精度越高；是基于相对比误差的精度度量，刻画预测结果与观测值的平均偏离程度；表征预测值与观测值之间的相关性，其越接近1，则预测值与观测值的时间序列的关联度越高；的值越接近1，则模型的输出值或预测值与观测值的误差越小。

3.2 测试事例及分析

基于2020年全国研究生数学建模竞赛E题提供的视频帧和能见度标签数据，选取分辨率为320×320的1862幅灰度图及对应的观测能见度值构成样本集Σ，每张图像内包含目标物灯塔和天空信息，部分灰度图如图3所示。

图3 不同能见度下样板图像示例Fig.3 Example of sample images at different visibility levels

由图3的视觉效果可知，随着时间的推移，雾的浓度越来越大，目标物体灯塔的可见性越来越差，且逐渐模糊，即图像的能见度距离逐渐变低。该视频在较长时间段内，目标物体的可见度都很低。

3.3 实验结果与分析

将样本集Σ中的样例作为DFNN及参与比较模型的输入，获得各模型输出神经元输出的能见度值和下一时刻的预测值，依据评价指标获得各自的评价指标值，见表1。另外，各模型作用于Σ中时间序列样例，获得的能见度预测曲线与观测值曲线比较如图4所示。

表1 算法的误差性能比较Tab.1 Comparison of error performance of algorithms

图4 不同能见度下模型的能见度预测值与观测值对比Fig.4 Modeled visibility predictions versus observed values at different visibility levels

由表1可知，DFNN获得的均方根误差值最小且与其它模型获得的值偏差较大，说明DFNN获得的能见度预测值时间序列与能见度观测时间序列的离散程度较低，因而其预测雾天环境下能见度的稳定性较好；MLP获得的值最大，说明将输入灰度图的灰度值直接用于训练神经网络模型会导致MLP的预测值与观测值的离散程度高，模型预测的稳定性较差；CNN和VisNet获得的相对于MLP的值偏小，说明将输入灰度图作特征提取有助于改善模型预测效果的稳定性。由各模型获得的指标值可知，DFNN的能见度预测效果最好，VisNet次之，而MLP的预测效果最差。由指标值获知，DFNN获得的值接近0，表明其在各个时刻获得的能见度预测值较为逼近观测值，但其它模型却相反，即在特定的时刻或时间段出现预测误差偏大。另外，DFNN和VisNet得到的值已接近1，说明这两种模型获得各时刻的能见度预测值与观测值高度相关，因此模型的拟合能力强；虽然MLP和CNN得到的能见度预测值与观测值也具有一定的相关性，但模型的拟合能力相对较差。最后，指标的值表明，DFNN的模型预测精度高，VisNet次之，而MLP最差。概括起来，DFNN具有最好的实时能见度预测效果，其预测精度高且稳定，VisNet次之，且MLP对实时预测能见度的能力偏弱。

由图4可知，因MLP未涉及图像的特征提取，所以其解决能见度时间序列预测问题的能力较弱，且预测效果出现明显不稳定的现象；CNN的能见度预测效果比MLP的要好，但预测效果的波动性较为明显，且在预测后期，预测曲线与观测值曲线存在一定的偏离；VisNet的预测效果比CNN要好，且预测值与观测值的偏差较小，但预测曲线在后期出现波动现象；DFNN明显优于参与比较的模型，能快速地在预测初期使预测值与观测值的偏差变小，所得预测曲线逼近观测值曲线的程度较高，且预测效果未出现波动现象，因此其较适合基于图像的预测问题。

4 结束语

能见度估计一直是交通出行与管理关注的重要话题，也是计算机视觉领域的重要课题。本文在分析果蝇视觉信息处理与传递的生物学原理基础上，基于果蝇的视觉信息处理机制和学习特性，以及梯度下降算法，获得一种深度果蝇神经网络模型。计算复杂度分析表明，该模型的计算代价主要由其输入分辨率确定。实验结果表明，此模型应用于时间序列能见度预测问题，具有较好的预测能力和抗干扰能力，预测效果稳定，实时能见度预测精度高。此外，该模型虽能满足实时性要求，但环境的自适应能力有待进一步开展研究。