地铁车辆制动电阻风机自动控制策略研究

朱韦祯，杨 俭，袁天辰，宋瑞刚

（上海工程技术大学 城市轨道交通学院，上海 201620）

0 引 言

地铁在制动过程中将牵引电机充当发电机，将车辆动能转化为电能，进而采用再生制动和电阻制动的复合制动方式实现停车。制动电阻作为车辆电制动系统的重要组成部分，承担车辆再生制动时电网无法消纳的多余制动电能消耗任务。为确保制动安全而设计的制动电阻风机功率大，且增加了车辆运行过程中的空气噪声。现今地铁城市运行图不断优化，车辆发车间隔随客流量而变化，并伴随储能技术的多样化工程应用。这将使得车辆再生制动产生的能量回馈吸收的比例在特定时段内大幅增加，从而使制动电阻实际功率消耗减少。

风机可通过调速的方式减少电能消耗，工业上异步电机采用变频控制技术调速性能优越。基于计算机数值仿真可提高风机调速设计效率。本文将建立风机数学模型，通过计算机仿真实现风机控制的设计。另外，风机的调速信号将由设置的电阻温度控制器提供。工业上广泛应用的温度控制器一般采用PID控制器，由于智能算法的出现，利用传统算法与智能算法复合控制将大幅提高控制性能。本文设计制动电阻温度控制器，通过设计模糊算法实时优化PID参数，使控制系统输出响应性能更快速平稳。

1 制动电阻使用工况分析

地铁车辆制动以电气制动为主，机械制动为辅。电气制动的过程中，再生制动能量反馈和电阻制动耗能占总电气制动能量的比例随列车路网运行变化而变化。地铁车辆在不同运行间隔时再生制动和电阻制动各占总电气制动百分比，见表1。

表1 电气制动各部分百分比Tab.1 Percentage of each part of electric braking

可见制动电阻运行工况随列车运行图变化而变化，当列车运行图发车间隔较短时，大部分制动能量被吸收，仅有小部分能量需要制动电阻消耗；当列车发车间隔较大，车辆电气制动产生的能量无法吸收时，制动电阻需要承担主要制动能量消耗。

由于绝大部分城市地铁客运都因为上下班客流而将运行图分为高峰时段和平峰时段，因此绝大部分车载制动电阻工作都面临不规律变化的问题。制动电阻风机通常功率大，斜流通风机功率达11 kW，制动电阻斜流通风机铭牌参数见表2。故斜流通风机的功率浪费及空气噪声问题亟待解决。本文将通过温度控制器控制制动电阻的风机变频调速，在满足电阻散热功率的前提下提高制动电阻风机工作效率。

表2 制动电阻斜流通风机铭牌参数Tab.2 Parameters of brake resistance diagonal fan nameplate

2 斜流通风机转速控制

斜流通风机驱动电机为三相异步电机，异步电机的调速控制技术发展多元，为满足制动电阻空气对流散热，采用矢量控制技术，使风机转速满足电阻散热功率变化的需求。建立准确的风机数学模型是后续准确仿真风机工作性能的关键。

2.1 风机矢量控制数学原理

三相异步电机具有高阶次、非线性、多变量耦合的复杂特性，很难直接构建数学模型进行仿真控制。矢量控制技术则将异步电机在连续坐标变换下等效成直流电机，对定子电流完全解耦为独立的励磁电流和转矩电流进行控制，可使风机具有良好的调速性能。风机的矢量控制原理如图1所示。

风机等效为直流电机，在数学推导上存在两种变换，即Clarke变换（3S／2S）和Park变换（2S／2R）。

（1）Clarke变换。Clarke变换将三相静止坐标系映射到两相静止坐标系，3S／2S变换结构如图2所示，可推算变换前后电流关系，式（1）。

图1 矢量控制原理图Fig.1 Schematic diagram of vector control

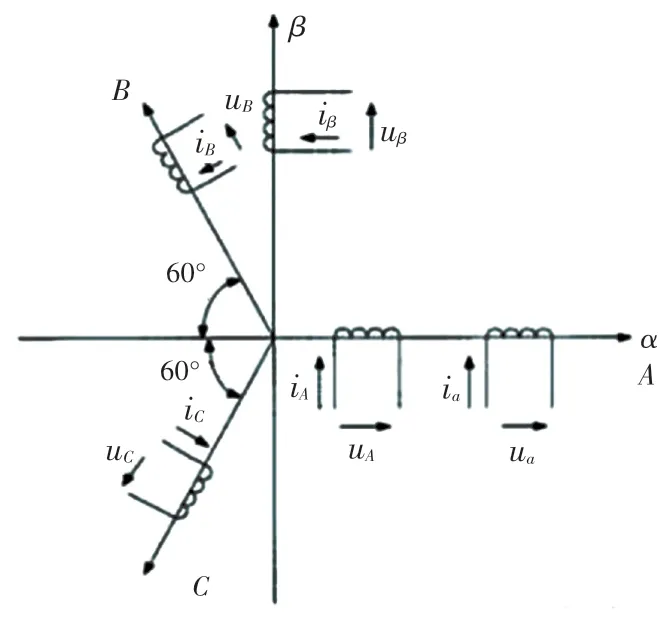
图23S／2S变换结构图Fig.23S／2S transformation structure

（2）Park变换。Park变换将两相静止坐标系映射到两相旋转坐标系，变换结构如图3所示。

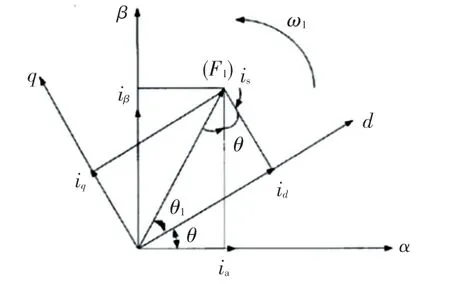
图32S／2R变换结构图Fig.3 Structure diagram of 2S／2R transformation

推得电流关系，式（2）～（3）：

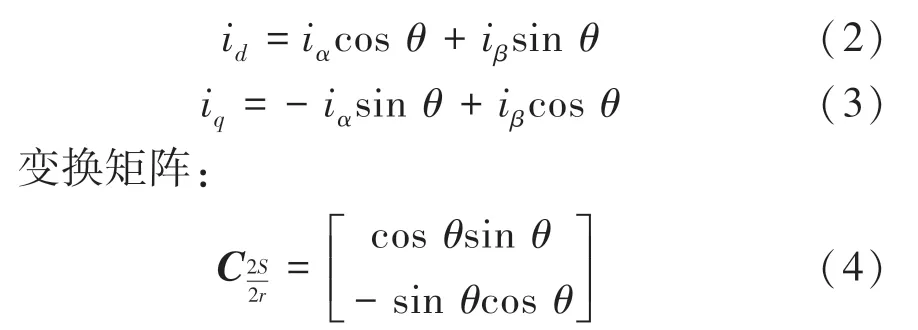
通过坐标变换得到各坐标系下的风机数学模型是研究风机动静态性能的基础。本文选用基于转子磁场定向的矢量控制，即在两相同步旋转坐标系下，使轴与转子总磁场保持一致，将轴同总磁场方向保持垂直，构成转子磁场定向的旋转坐标系（坐标系）。推得该坐标系下的控制方程。

（1）风机电磁转矩方程，式（5）：

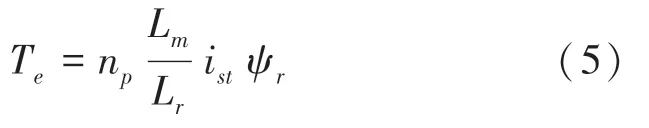
其中，n为极对数；L为互感；L为折算到转子电感；i为定子电流转矩分量；ψ为转子磁链。

（2）风机转子磁链方程，式（6）：

其中，T为转子励磁常数；为微分算子；i为定子电流励磁分量。

（3）风机转差频率方程，式（7）：

通过以上方程转换可将风机模型解耦为等效直流电机模型。

建立转子磁链模型，可解决工程现实中磁链难观测的问题，以理论计算结果替代观测值。

2.2 风机控制Simulink仿真

MATLAB／Simulink提供了动态系统仿真分析环境，基于风机矢量控制的数学模型推导，可通过模块库里的模块组合、封装，搭建构成风机的数值仿真模型，从而验证系统调速性能。

针对风机的矢量控制的数学模型，对坐标变换模块、角度计算等模块进行搭建和封装，组成完整的调速系统。

（1）坐标变换模块。由3S到2S再到2R的电流坐标变换仿真图如图4所示。

图4 坐标变换仿真图Fig.4 Simulation diagram of coordinate transformation

（2）角度计算模块。按风机角度计算公式搭建角度计算仿真图如图5所示。

由于篇幅限制仅列出以上两个子模块，由各模块搭建封装后组成的风机矢量变频调速仿真模型如图6所示。

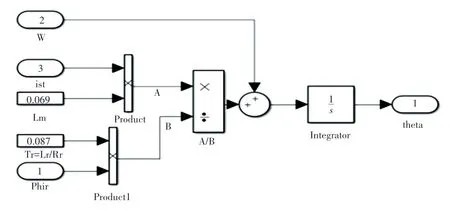
图5 角度计算仿真图Fig.5 Simulation diagram of angle calculation

图6 风机矢量控制仿真图Fig.6 Simulation diagram of fan vector control

2.3 仿真结果分析

仿真模型给出模拟风机转速激励曲线，通过示波器观察斜流通风机在给定转速变化曲线下电机实时转速变化，如图7所示；三相定子电流的变化曲线，如图8所示；电机磁链观测图如图9所示。可知，风机基于电流滞环比较的矢量变频控制系统的转速控制响应速度快且变化平稳，稳态性能可以满足制动电阻运行下对温度控制器做出判断后输出转速控制信号的响应性能要求。

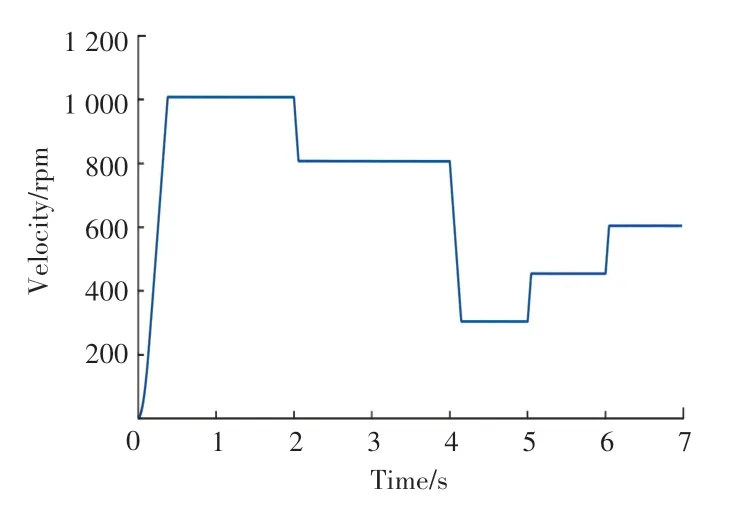
图7 风机转速曲线图Fig.7 Fan speed curve

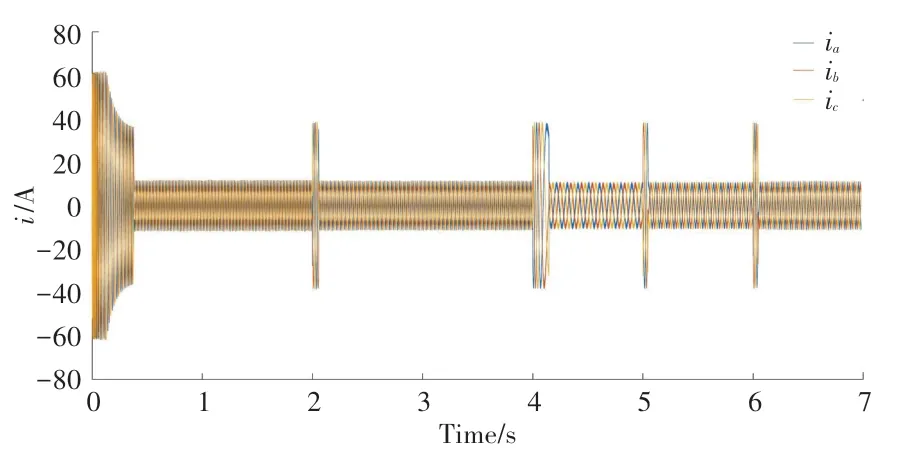
图8 电机三相定子电流变化图Fig.8 Three phase stator current variation diagram of motor

图9 磁链观测图Fig.9 Flux observation diagram

3 制动电阻温度控制

工业温度控制多数采用PID控制算法，虽简单、可靠性高，但其应用对象为大惯性、时滞、非线性、时变的复杂系统时，控制效果较差。诸如粒子群算法、模糊算法等现代智能算法的出现，很大程度上提高了控制器的自适应度，从而避免了因被控对象难以精确建立数学模型导致的控制缺陷。本文制动电阻温度控制器采用PID算法，并嵌入智能模糊算法，以期得到更稳定的动态控制效果。

3.1 温度的PID控制

PID控制器通过对制动电阻采集的温度与设定温度误差量的比例、积分、微分进行线性组合来提高控制的静、动态性能。其具有结构简单、可靠性好等优点而被广泛应用，其原理框图如图10所示。

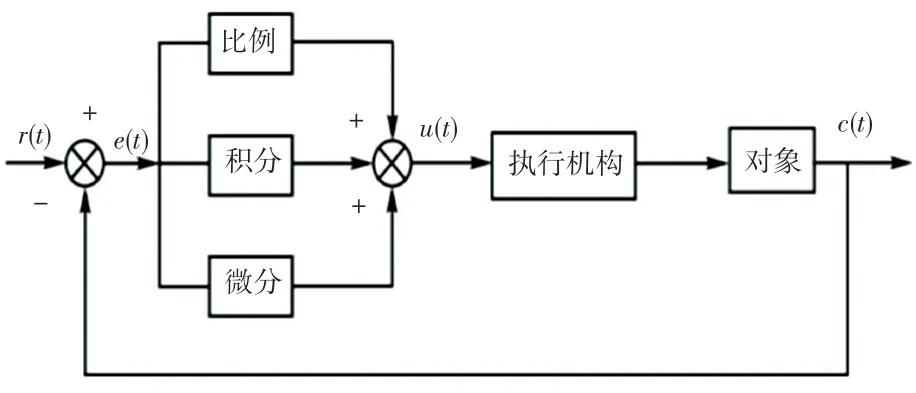
图10 PID控制系统原理图Fig.10 Schematic diagram of PID control system

控制方程如式（10）：

式中，K为比例增益；K为积分系数；K为微分系数。

3.2 温度的模糊PID控制

制动电阻温度变化具有时延和惯性，采取单一的PID控制又无法对比例、积分、微分参数实时整定，故将模糊算法嵌入PID控制，以提高参数的自适应能力，可提高温度控制器的性能。

3.2.1 温度模糊PID控制

根据制动电阻温度变化的工程数据和经验设计模糊算法对温度PID控制的参数在线整定。以制动电阻温度变化及其变化率为输入来对K、K、K实现在线自整定。设制动电阻温度实际值与设定值之间的偏差为。模糊控制的输入为温度偏差及温度偏差变化率，输出为ΔK、ΔK、ΔK。 PID控制器系数变化如式（11）：

模糊控制器对PID参数实时整定的框图如图11所示。

图11 模糊PID控制框图Fig.11 Fuzzy PID control block diagram

3.2.2 模糊控制器输入输出变量

模糊控制器输入设置为电阻温度变化及其变化率变量和，输出变量为参数增量ΔK、ΔK、ΔK。模糊子集设为｛负大、负中、负小、零、正小、正中、正大｝，简记为｛NB、NM、NS、ZO、PS、PM、PB｝，量化论域为｛3、2、1、0、1、2、3｝。输入输出变量均采用三角形函数作为隶属度函数。寻找、与ΔK、ΔK、ΔK之间的关系，从而实现对K、K、K的在线实时整定。

3.2.3 模糊规则的建立

地铁制动电阻温控系统的参数整定基于人工经验，制定以下基本规则：

温度误差较小，K、K应取较大值，可保证系统的稳态性能，K取值应适中，避免温控系统的超调；

温度误差适中，K取较小值，可减小温控系统超调量，K、K取值应适中；

温度误差较大，K取较大值，加速系统响应速度，K、K取值应适中。

依据经验制定模糊控制规则见表3。

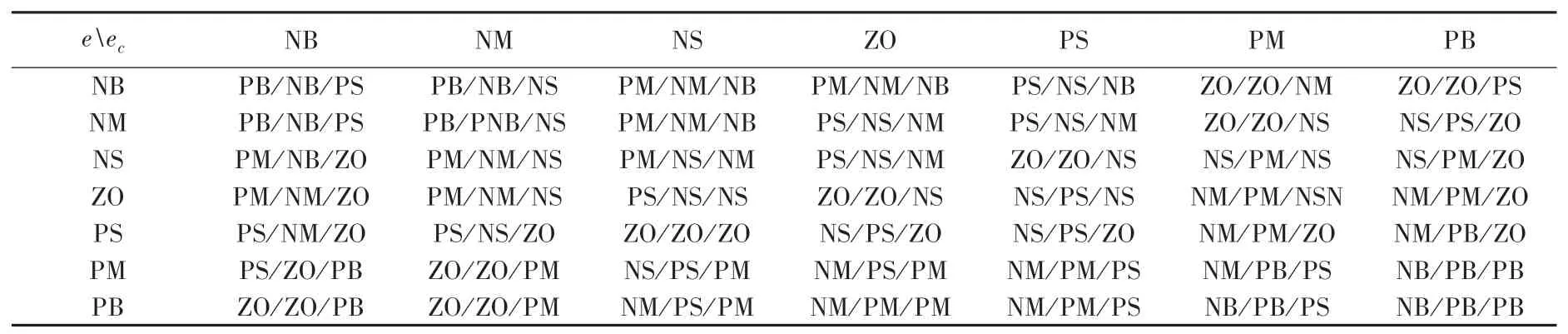
表3 温度模糊控制规则表Tab.3 Temperature fuzzy control rule table

3.3 温度控制Simulink仿真

制动电阻温度具有时滞、大惯性、变参数的特点，因此难以建立精确的数学模型，可将温度系统简化为一阶惯性系纯滞后环节。可设置系统传递函数如式（12）：

在MATLAB／Simulink中采用传递函数验证制动电阻温度变化在PID控制下和模糊算法优化PID控制下对模拟外激励的动态响应。PID与模糊PID控制对比仿真图，如图12所示。

由阶跃信号作用下PID与模糊PID温度控制仿真图如图13所示，在PID控制和模糊自适应PID控制下，系统达到稳定所需时间近似相等，但加入模糊算法后系统超调量大，反复震荡的现象得到大幅改善，这将为输出平稳的转速控制信号提供保证。

图12 PID与模糊PID控制对比仿真图Fig.12 Simulation chart of PID and fuzzy PID control

图13 PID与模糊PID温度控制仿真曲线图Fig.13 Simulation curve of PID and fuzzy PID temperature control

4 结束语

制动电阻作为地铁车辆再生制动过程中的间歇性工作单元，确保其散热正常的前提下，可对风机做出节能控制改造。本文以建立风机数学模型为基础，并设计制动电阻温度控制器，在模糊算法优化参数状态下提高温控系统的性能，并借助MATLAB／Simulink对风机变频矢量控制进行数值仿真验证其性能。基于计算机仿真可见风机调速误差小、响应速度快，性能可满足制动电阻正常工作对风机的使用要求。温度控制器在PID算法基础上通过模糊算法在线整定PID参数的方式使温度控制器减小超调量，鲁棒性提高，自适应能量增强。制动电阻风机通过温度实时监测的方式调整运转功率，既能满足散热需求，又能降低风机功耗和噪声，采用上述方法能使制动电阻适应大规模再生制动过程的多变工况下实现节能要求。