为知识生长寻找源头

范林伟

在教学除法的初步认识时，教师通常先以“平均分”引出除法，再辅以“包含除”来帮助学生实现除法的双重意义的完整建构。这样“顺应式”的学习也能使学生理解其意义、感受其异同。那么，教学能否立足学生的最近发展区，让学生进行“同化式”的学习，在已有的知识经验的基础上生长出新知呢？下面，笔者以特级教师朱国荣的“除法的初步认识”一课为例，谈谈对其创新教学的学习与体会。

一、在前置练习中催生新知

教师利用前置练习“20个苹果，每4个装一盘，能装几盘”展开教学，引导学生在对比与辨析中建立知识间的联系。

教师出示作品1（如圖1）。

师：他用了什么方法解决了这个问题？在他画的图上能数出答案吗？

师（小结）：他是用画图的方法来解决问题的，有5个4，就能装成5盘。

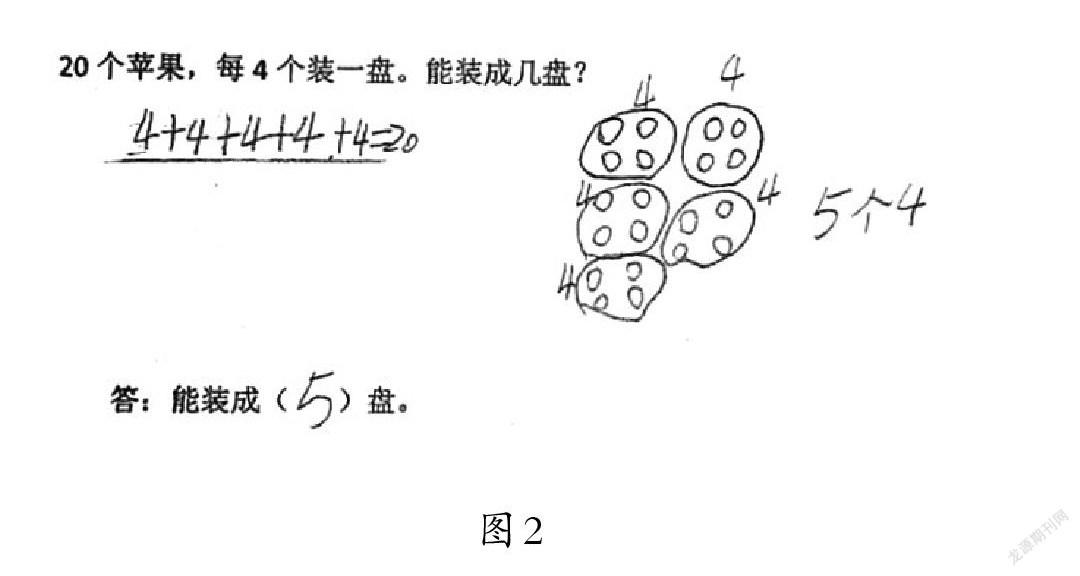
依次出示作品2（如图2）和作品3（如图3）。

教师组织学生对作品进行解读，并相机板书：

加法：4+4+4+4+4=20（个）。

减法：20-4-4-4-4-4=0（个）。

师：在加法算式中，要加几个4？在减法算式中，要减几个4？

师：在他们的加法和减法算式中，你们能看出答案是几盘吗？

生：5盘。

师：谁上来圈一圈，5个4在哪里？

师（小结）：20里面有5个4，答案就是5盘。

师：在减法算式中，你看到5盘了吗？

（学生回答后，教师圈出减法中的5个4）

师：同学们想一想，要求能装几盘就是求什么？

生：求能装几盘就是求20里面有几个4。

师：在解决这个问题时，我们可以用画图的方法，也可以用加法或者减法。这两个同学把画图的方法升级成了加法和减法，真的很厉害！你们还有别的方法吗？

生：我用了除法。

生：我用了乘法。

【赏析】课始，教师利用前置练习生成的作品组织教学，从画图到算式，从直观到抽象，引导学生在对作品的解读中感受解决问题的不同策略。这一环节不仅激活了学生用同数连加、同数连减的方法来解决问题的经验，而且还以直观的图示来支撑数学思考，以圈出相同数据这一动作为后续乘、除法的自然生长以及相互之间的类比、迁移做了铺垫。

二、在方法的升级中构建新知

师：想一想，这样的加法算式升级之后会变成什么方法？

生：我觉得这样的加法会升级成乘法。

师：5个4相加写成乘法，你们会吗？看！有个同学已经写好了！

教师出示作品4（如图4）。

师：4×5=20（个），在他的这个算式里，你们能看到5盘在哪里吗？用手指一指。

师：4×5=20，5是怎么想出来的？

生：想乘法口诀“四五二十”。

师：我们把加法升级好了，想一想减法怎么升级？猜猜看，减法升级之后会变成什么？

生：除法。

师：你会写这个除法算式吗，谁来写一写？

[学生板演：20÷4=5（盘），教师结合学生书写的算式介绍除号和写法，以及除法算式的读法]

师：想一想这个算式求的是什么？

生：求20里面有几个4。

师：这个算式的答案是5，又是怎么想出来的呢？

生：想“四五二十”就可以算出结果了。

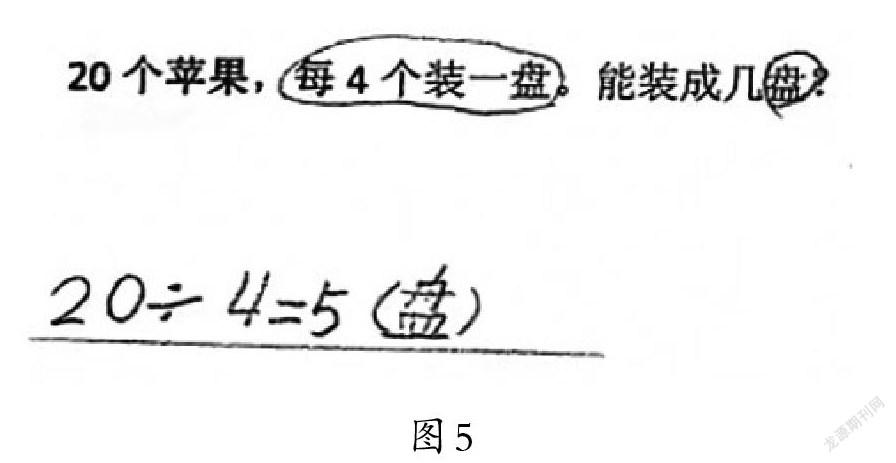
[教师出示作品5（如图5）]

师：看，昨天就有同学是这样想的。同学们，今天我们学习了一种新的运算方法——除法。（板书课题）接下来，老师想请大家用除法来解决问题。

……

【赏析】教师充分预设学情，鼓励学生基于“同数连加可以写成乘法算式”的经验进行迁移，生成出“同数连减可以写成除法算式”。这一实践为除法的产生开拓了一条新的途径，为除法的生成寻找到了知识的源头。在这一类比过程中，“加法升级为乘法”为学生提供了求简的体验，为学生将“减法升级为除法”提供了心理上的准备;“乘法口诀求商”，为学生获得除法算式的结果提供了方法的支撑。整个教学过程如行云流水，朱老师既展示了除法算式的形成过程，又揭示了除法的本质意义，还让学生感受了除法的简便性。

三、在知识运用中丰富意义

1.出示问题

30个小朋友做游戏，每5个人一组，能分成几组？

师：能分成几组就是求什么？

生：就是求30里面有几个5。

（学生列式计算）

师：要知道30÷5等于几，应该怎么想？

生：要想“五六三十”就知道答案了。

师：这个问题你们还愿意用画图的方法来解决吗？愿意用减法来解决吗？如果用减法算式应该怎么列式？谁来说一说！要减几个5？

生：这样写太麻烦了，还是除法简单。

2.出示问题

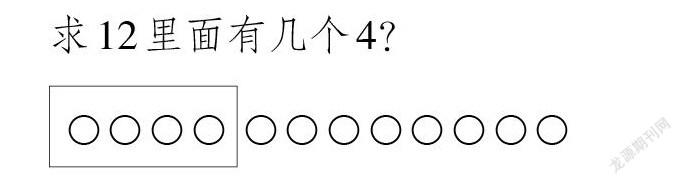
求12里面有几个4？

师：想一想，求12里面有几个4应该怎么列式？

生（齐）：12÷4。

师：接下来，老师给大家几个生活中的问题，请你们想一想这里哪些问题可以用12÷4来解决，还有哪些问题不是求12里面有几个4，不能用12÷4来解决。

（1）有12颗糖，每人分4颗，可以分给几人？

（2）有12颗糖，吃掉4颗，还剩下几颗？

（3）有12颗糖，平均分给4个人，每人分几颗？

（学生四人小组讨论，分享想法）

生：第2个问题不可以用12÷4=3。吃掉4颗应该用减法，不能用除法。

师：为什么用减法呢？

生：吃掉就是从12颗里拿掉4颗。

……

【赏析】通过对同类问题的分析和生活情境的辨析，学生再次感受除法的简便性，深入理解除法的意义。同时，进一步使学生理解“只减一次用减法”“同数连减可以用除法”。当然，除法的意义包括“包含除”与“平均分”两类，“同数连减用除法”是从包含除的角度切入的，学生比较容易理解。但是，“平均分”如何纳入这一结构呢？学生理解就有了一定的难度，于是朱老师就依托有趣的分糖游戏，巧妙地帮助学生实现了数学理解，完成除法意义的双重建构。

3.游戏环节

师：我们先来看看第1题，它是在求12里面有几个4吗？（是的）那第3题是不是也在求12里面有几个4呢？（等待）看来这个问题有点难，我们来做个游戏好吗？

（教师选择4名学生上台演示分糖过程）

师：12颗糖，平均分给4个小朋友，怎么分？

生：每人分3颗。

生：一颗一颗地分，如果分完之后还有多，再一颗一颗地分，直到分完为止。

师：有4个同学，我一次先拿几颗糖出来分？（4颗）这算是分了一次，分完了吗？（没有）现在谁知道，一共能分几次？

生：3次。

师：你们怎么知道一共能分3次，怎么想出来的？

生：三四十二。

师：总共有几颗糖？每人分一颗，一次分几颗？12里面有几个4？

生：12里面有3个4。

师（小结）：第2题不用能12÷4，第1、3两题都可以用12÷4，因为它们都是在求12里面有几个4。

4.练习巩固

教师出示习题：有□颗糖，平均分给6人，每人分几颗？

师：有18颗糖，平均分给6人，每人分几颗？

生：每人分到3颗。

师：想一想，除法算式应该怎么列式？

生：18÷6=3（颗）。

生：有42颗糖，平均分给6人，每人分几颗？

生：每人分到7颗，列式是42÷6=7（颗）。

师（小结）：今天這节课我们学习了什么？你们对除法有什么新的认识？

生：除法是减法的简便运算。

生：除法就是把乘法倒过来，

师：你们还有别的问题想问吗？

生：有没有除法口诀？

师：你们觉得除法要不要编口诀，有没有必要？

生：不需要除法口诀，因为乘法口诀就能解决除法的问题。

【赏析】教学中，教师通过现场的分糖游戏，使学生见证“每人分1颗，分一次要4颗，分3次才能分完，即12里面有3个4”。这样，巧妙地将“平均分”与“包含除”统一起来，使学生感悟到这也是“同数连减”，从而建立对平均分的认识。然后，教师及时地借助开放性的练习巩固知识，让学生深入理解除法的意义及其求商的方法。在课堂小结中，我们也能发现学生对于除法的意义的理解是十分丰富的，既感受到除法的简便性，又感受到了除法与乘法之间的互逆关系。

四、在对比练习中感受区别

1.有12根香蕉，每3根装一盘，能装几盘？

2.有12根香蕉，吃掉3根，还剩几根？

3.有12根香蕉，平均分给3只小猴，每只小猴分几根？

（学生列式计算，教师逐题反馈）

师：想一想，在解决第1题和第3题时需要注意什么？

生：单位不一样。

【赏析】教师再次运用对比练习，组织学生在独立解决问题的过程中深化对除法意义的理解，同时依托对单位名称的辨析，使他们体会“包含除”与“平均分”之间的差异。

整节课，朱老师始终立足学生视角进行教学，循序渐进地帮助学生建构新知。他首先依托前置练习诊断学习起点，使学生不断体会连减的过程。然后，以“同数连加升级成乘法”为切入点，激活学生“同数连减升级成除法”的意识，使学生感悟到“求一个数里面有几个几可以用除法表示”。同时，朱老师创设分糖果的游戏来引领学生突破关于平均分的学习难点，感受平均分也可以用除法计算。教学中，朱老师设计了针对性的练习来巩固学生关于除法的认识，使学生深刻体会到“除法是同数连减的简便运算”“除法是乘法的逆运算”，还通过对单位名称的比较使学生体会了除法的双重意义之间的联系与区别。

（作者单位：浙江师范大学附属嘉善实验学校）

投稿邮箱：405956706@qq.com