基于贝叶斯理论嵌套抽样的结构物理参数识别研究
王坤阳, 公茂盛, 左占宣
(中国地震局工程力学研究所,中国地震局地震工程与工程振动重点实验室,哈尔滨 150080)
结构健康监测是目前土木工程领域较为热门与重要的研究方向,而结构损伤识别是结构健康监测技术的核心。结构损伤通常表现为刚度的退化,因此对结构物理参数(如刚度)进行识别对于结构损伤识别是尤为重要的。常用的根据振型、频率等模态参数进行识别的确定性方法因为环境噪声、仪器及复杂的结构属性的影响使得观测数据中存在很大的误差,大大增加了参数识别中的不确定性[1-2],因此基于不确定性的结构损伤识别方法研究是十分必要的。
1989年,Beck[3]基于贝叶斯框架提出了系统参数识别中处理不确定性问题的贝叶斯方法;Vanik[4]通过概率关系将贝叶斯方法应用到了结构健康监测之中。贝叶斯理论通过结构输入与输出的关系,建立后验联合概率密度函数来计算待识别参数的概率密度值并进行参数估计。实际结构的待识别参数是十分复杂的,所以在结构物理参数识别中,后验联合概率分布通常是复杂、高维的,常用的物理参数识别的贝叶斯估计渐进逼近方法[5](asymptotic approximation methods)面对高维概率分布问题难以求解。Beck等[6]提出了利用马尔可夫蒙特卡洛(MCMC)抽样方法来解决高维概率分布问题。Sohn等[7-12]使用该方法对不同结构模型的结构物理参数进行了识别。
传统的马尔可夫蒙特卡洛方法面对高维概率密度分布时会出现不收敛、采样效率低与识别结果误差较大等问题。Cheung曾通过使用混合蒙特卡洛模拟(hybrid Monte Carlo simulation)的方法代替传统的马尔可夫蒙特卡洛抽样方法,虽然提高了抽样效率,但仍存在识别结果误差较大的问题[13]。
Skilling[14]在2004年提出了针对解决贝叶斯公式中高维概率分布问题的嵌套抽样方法(nested sampling),不仅能加快抽样速度,更能根据自己的目标与需求来控制抽样进程,后来Speagle[15]对该算法进行了优化,提出了自适应嵌套抽样方法,并给出了嵌套抽样与自适应的嵌套抽样的相关算例与开源程序。曹彤彤等[16]通过嵌套抽样对地下水模型算例进行了研究,验证了其在模型选择中的有效性。嵌套抽样方法往往用于计算边缘似然值并进行模型选择,很少直接使用该方法计算整体边缘概率值并应用在结构的物理参数识别之中。本文提出基于加速度时程响应建立结构物理参数相关的后验联合概率密度函数,并通过插入不影响整体概率密度函数值的均匀分布π(θ),代替原有的先验分布并更改似然函数的方法,应用嵌套抽样对结构物理参数进行识别。采用所提方法分别对10层结构数值算例与一个3层振动台试验钢筋混凝土(RC)框架模型,进行结构物理参数识别,证实了方法在贝叶斯理论结构物理参数识别中不仅能很好的解决高维概率密度分布问题,精确估计待识别结构参数,并且在实际结构参数识别中也存在很好的适用性。
1 基本理论与方法应用
1.1 结构物理参数识别贝叶斯方法
对于Nθ个自由度的工程结构,根据最大熵原理,结构刚度参数θ服从正态分布,记θ~N(θMPE, 1),表达式如下
(1)
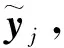
(2)
(3)
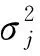

(4)
根据贝叶斯公式,可以求得基于实测响应的结构物理参数θ的后验联合概率密度函数

(5)
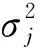

(6)
根据文献[17]的分析结果,式中c=0.2,通过式(5)、(6)即可通过抽样得到结构参数θ的最优估计值。
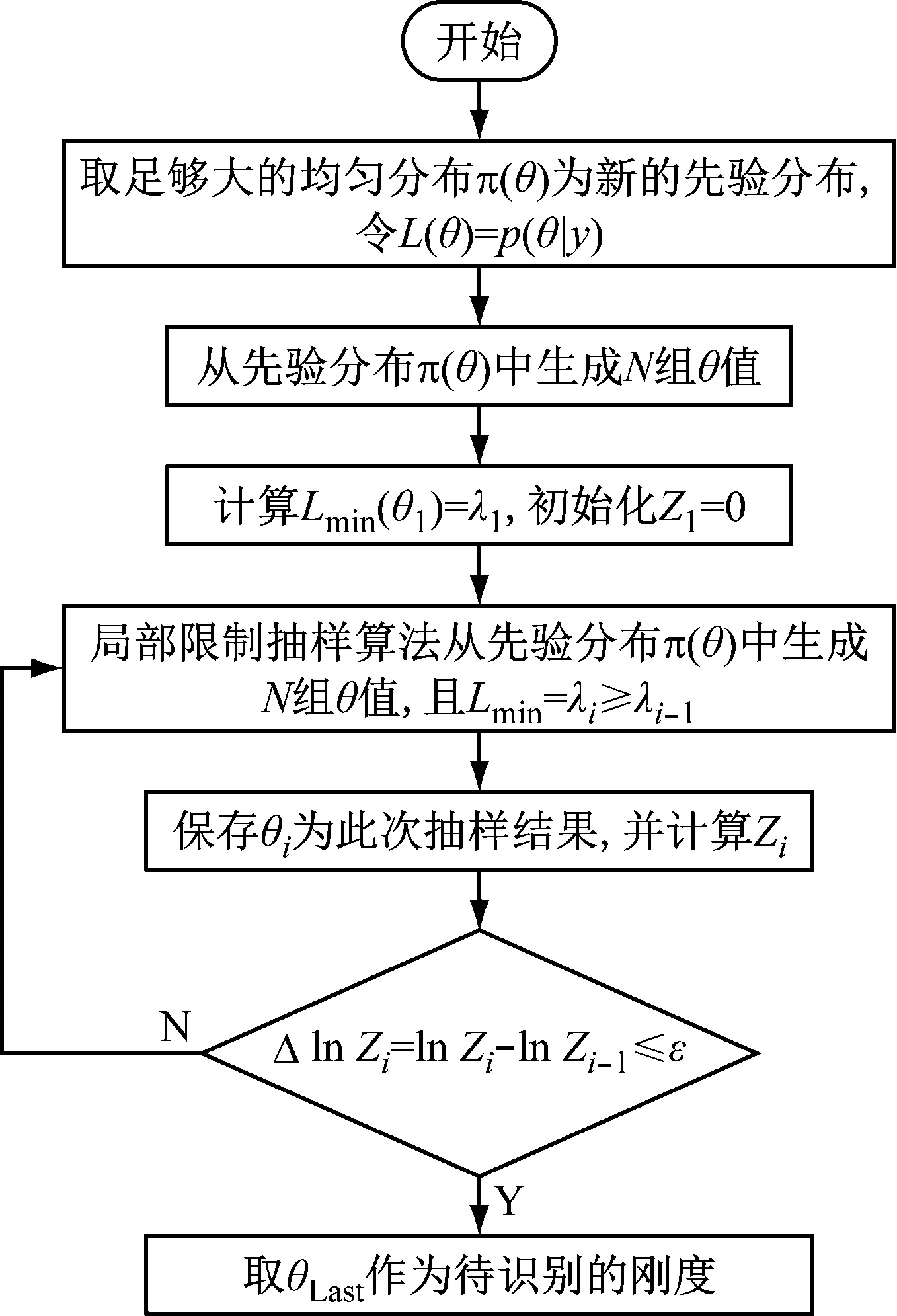
1.2 嵌套抽样方法理论及改进
直接应用嵌套抽样,在先验分布中生成样本,通过似然函数概率值进行选择,不仅会导致抽样效率低,还可能因为离开先验分布限制使得识别结果远远偏离真实值的情况出现。为解决这一问题,本文假设有取值范围足够大的均匀分布与原后验联合概率密度函数相乘并作为新的先验分布
π(θ)=1
(7)
由式(5)、(6)得

(8)
令原后验联合概率密度函数
(9)
代替成为新的似然函数,则有:

(10)

(11)
式(10)中dX是先验分布累积的微分。定义先验分布累积为
(12)
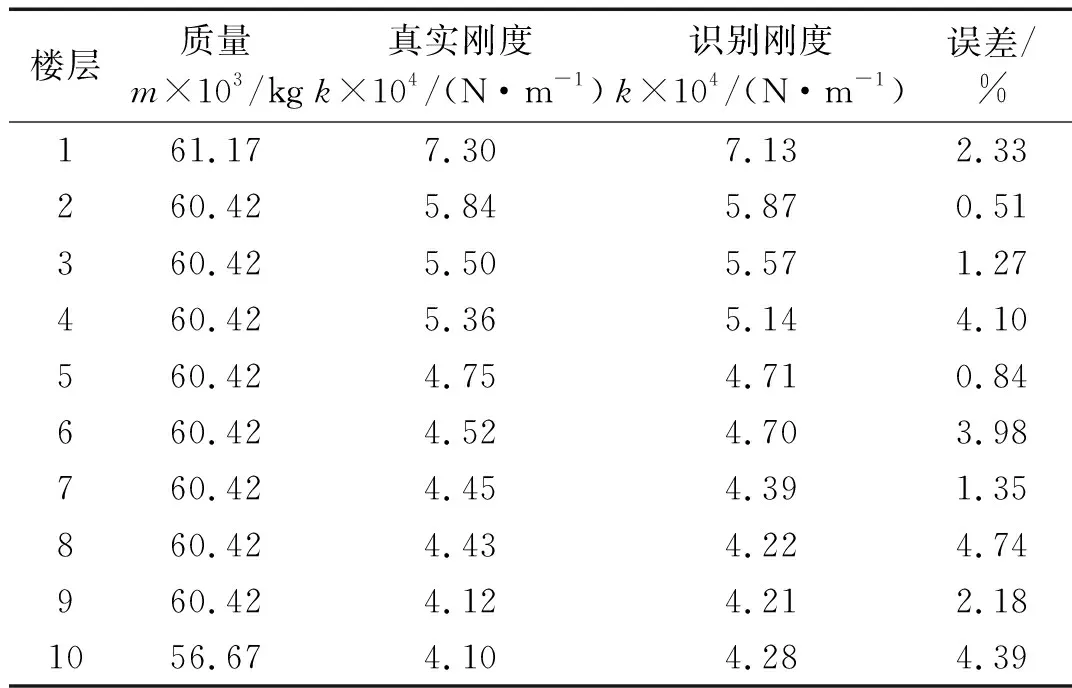
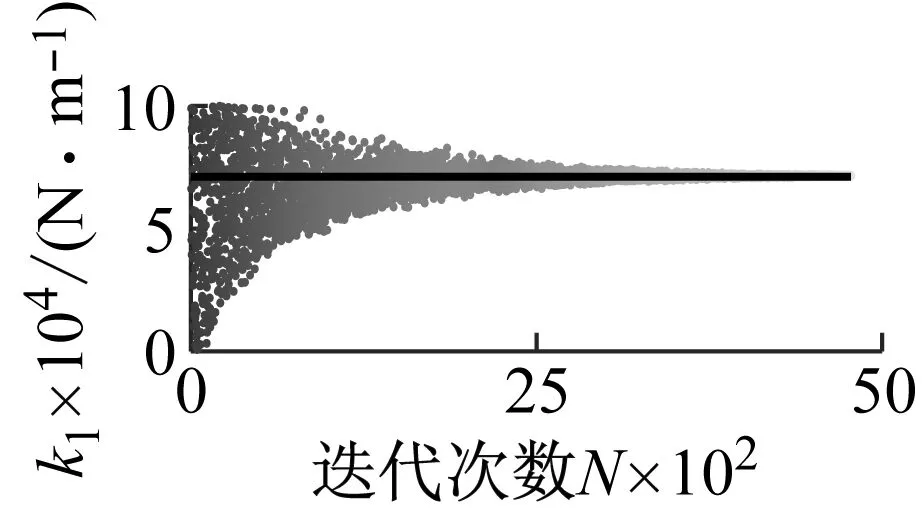
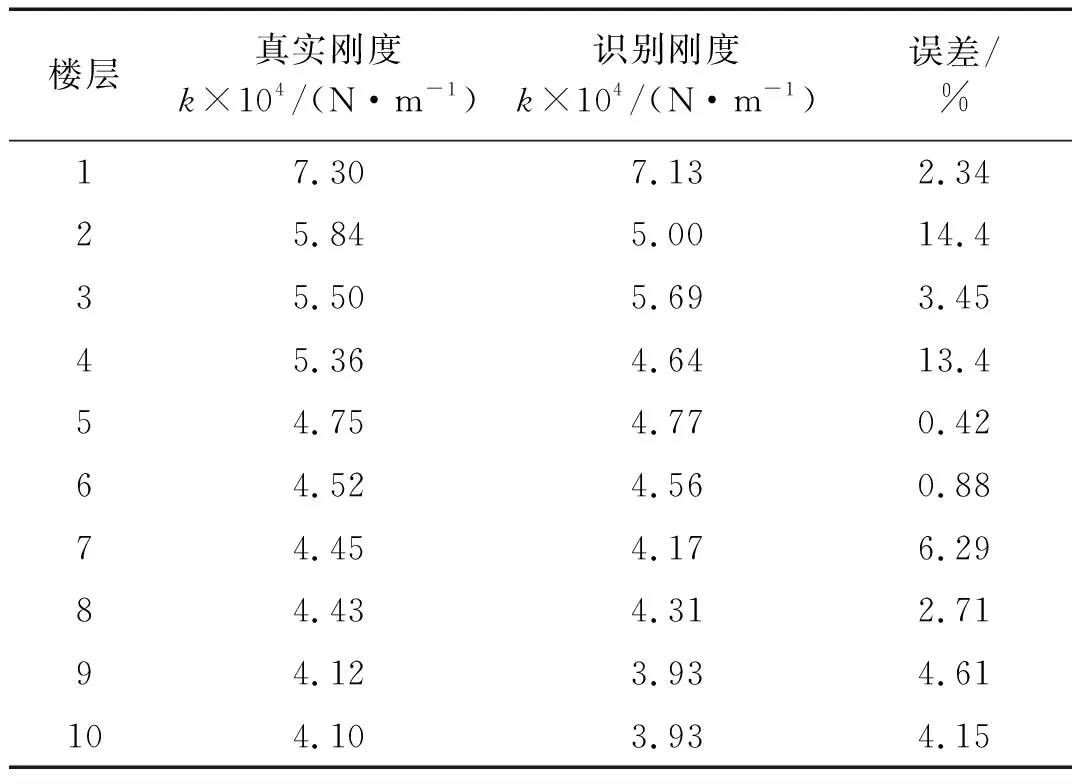
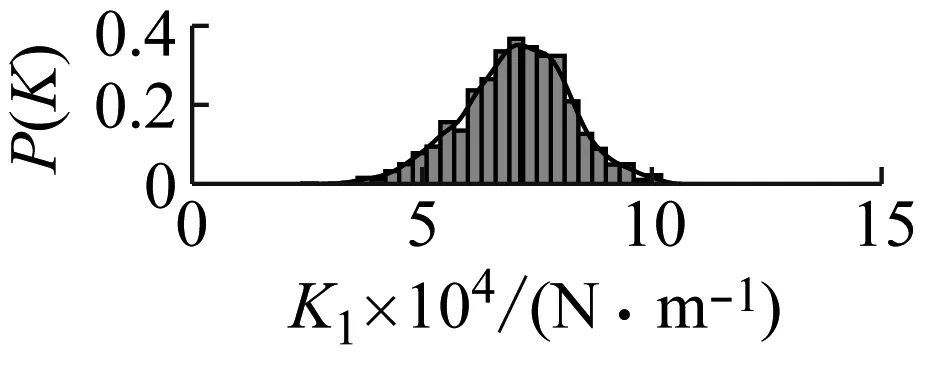
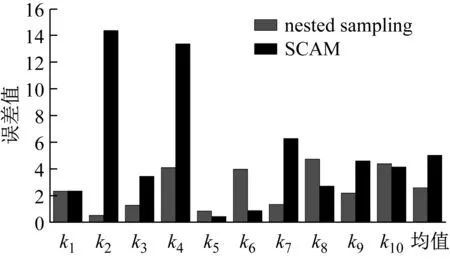
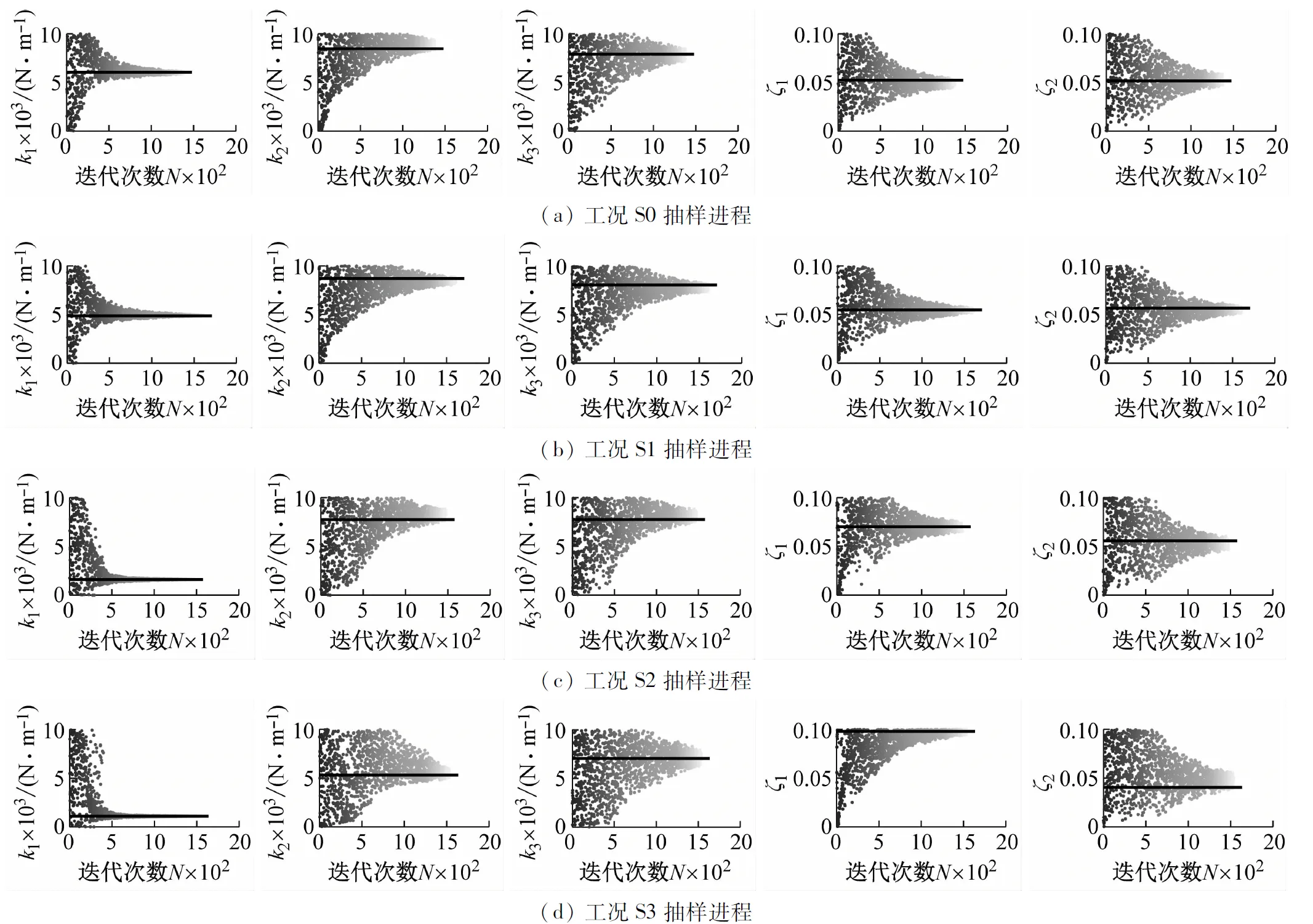
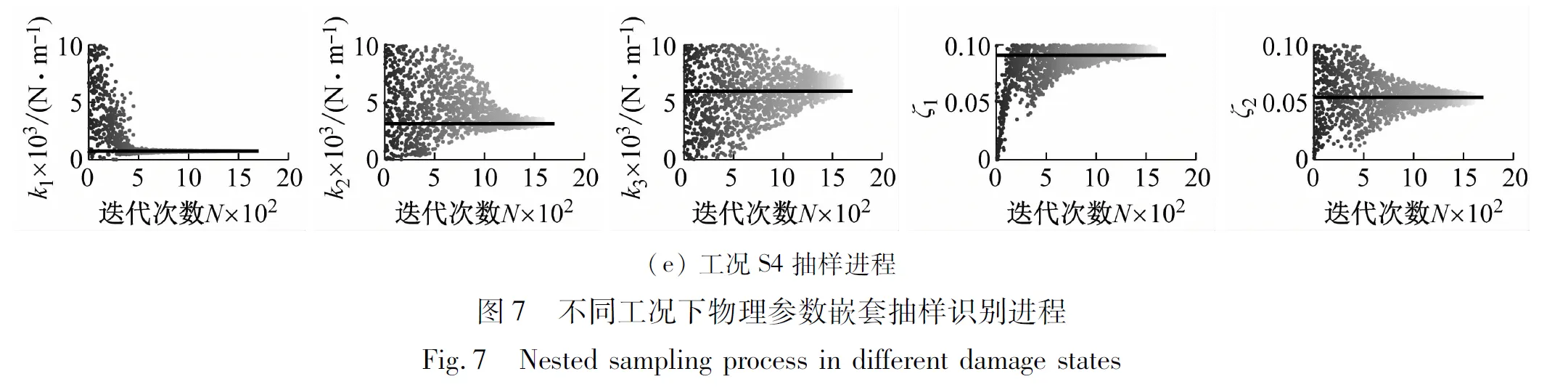
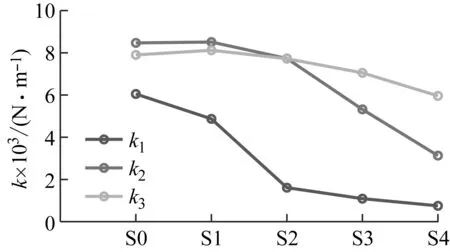
0 (13) 如上,通过将θ转换为X便实现了将多维问题转换为一维问题。为方便计算式(10),认为第k次抽样后 (14) 取式(13)作为抽样终止条件,其中ε为足够小得常数,通常令ε=0.01[18]。 ΔlnZk=lnZk-lnZk-1<ε (15) 随着抽样进程即可以得到Lmax(θ),即: (16) 通过建立新的先验分布与似然函数利用嵌套抽样性质,便可以取最后一步抽样得到的θ值作为近似最优识别值。具体嵌套抽样算法流程如图1所示。 图1 嵌套抽样算法流程图 因为土木工程结构复杂,贝叶斯理论结构物理参数识别应该考虑多参数的高维问题。本文建立了一个10层剪切结构模型,如图2所示,具体的结构设计参数如表1所示。 图2 10层剪切型结构模型示意图 表1 数值模型结构设计参数及识别结果 算例中,假定结构的阻尼比ζ不变且为0.05,待识别的物理参数有结构各层刚度θ=[k1,k2, …,k10]。对结构输入白噪声激励,通过Newmark-β法计算每一层的加速度时程响应,并在激励与响应中增加5%水平的白噪声模拟真实的输入与响应信息。令π(θ)中θ~U(0,10),代入式(9)得到后验联合概率密度后进行抽样。 根据式(15),当ε满足停止条件时,取最后一次抽样的样本点,即后验概率密度近似最大估计值作为刚度识别值,具体识别结果见表1。通过对数值算例结果分析,识别结果最大误差不超过5%,可见嵌套抽样能很好的解决基于贝叶斯的结构物理参数识别中的高维后验联合概率密度函数问题,且较为精确地识别结构物理参数。本文曾采用不添加噪声进行识别,识别结果的误差更小,说明所提方法有很好的抗噪性能,但由于篇幅有限,本文没有给出不考虑噪声的识别结果。 11例术后切口愈合良好,术后2周伤口拆线。治疗后疼痛均消失,足弓恢复,无跛行,术后随访3~18个月,未出现疼痛及其他并发症,恢复正常的生活及工作。末次随访时,AOFAS评分为平均(83.00±2.03)分(77~90分),优 4例,良5例,可2例。典型病例见图1。 图3 嵌套抽样进程 工程领域最为常用抽样方法为MCMC抽样方法,但当预估结构参数与实际结构参数相差过大或待抽样参数过多时,常常会导致抽样结果不收敛或不稳定。本文采用MCMC抽样中较先进的SCAM算法,对该10层结构数值模型进行了识别,识别结果如表2和图4所示。将该方法识别结果误差与本文嵌套抽样结果误差进行对比,结果如图5所示。 表2 SCAM方法识别结果 图4 SCAM抽样结果 图5 误差对比 通过对识别过程及结果分析可知,嵌套抽样方法可以通过控制终止条件使抽样结果更加的稳定,很好地解决了多参数抽样问题,且识别结果更精确。而从误差对比结果来看,MCMC方法的最大误差为14.4%,而本文方法最大误差仅为4.74%,两者相差3倍;从误差的平均值来看,MCMC方法误差的平均值为5.27%,而本文方法平均误差仅为2.57%,两者相差2倍。可见本文方法比传统的MCMC方法具有更高的识别精度。 为了验证基于贝叶斯理论应用嵌套抽样对于实际结构物理参数识别的适用性,本文对振动台试验中3层RC框架结构模型的层间刚度及阻尼比进行了识别。结构模型及结构尺寸简图如图6所示,具体的结构模型设计及试验工况等情况可以参考文献[19]。高艳滨曾通过Opensees有限元建模并对该结构进行Pushover分析,得到了该结构的初始状态物理参数估计值,具体结果如表3所示。 (a) 振动台试验模型 表3 初始状态结构参数估计值 通过振动台试验中结构加速度响应时程数据对结构物理参数及模态参数进行识别。当结构模型遭受低幅值白噪声激励时,一般不会引起结构的非线性反应,其响应主要与质量、刚度和阻尼比有关,假设结构质量保持不变,待识别的结构参数只有物理参数刚度以及模态参数阻尼比便只有刚度及阻尼比,即θ=[k1,k2,k3,ζ1,ζ2]。 该结构振动台模型试验中,根据输入地震动峰值加速度大小,可以分为S0、S1、S2、S4等四种损伤状态,其中S0是未输入地震动时模型初始状态,代表结构模型完好状态;S1为输入峰值加速度为0.1g地震动输入后损伤状态,结构模型发生轻微损伤;S2为输入峰值加速度为0.2g地震动输入后损伤状态,结构1层损伤严重,2层轻微破坏;S3为输入峰值加速度为0.4g地震动输入后损伤状态,柱底混凝土压碎,2层柱端开始出现裂缝;S4为输入峰值加速度为0.5g地震动后损伤状态,底层,2层均破坏严重,3层轻微破坏。分别用该结构S0~S4工况的白噪声响应进行识别,其抽样识别进程如图7所示,各个工况识别结果如表4所示。 表4 各工况结构参数识别值 从识别结果来看,S0状态识别结果与表2给出的初始值基本相同,随着加载工况的进行,结构发生了明显的刚度退化现象,具体如图7所示,由图可以推断结构在振动台试验中首先是第1层发生了破坏,其次是第2层发生破坏,最后是第3层,完全符合观察得到的试验现象。另外,本文结果与文献[20]对该结构试验模型的识别结果相比差别不大,也验证了本文识别结果的正确性。 图8 不同工况刚度识别值 为了查看识别效果,本文给出了识别结果和原始记录对比情况。因篇幅有限,本文只给出了S0和S4状态记录对比结果,如图9和图10所示,其余结果与此类似。通过图中计算加速度与观测加速度的对比可知,模拟识别的加速度时程与观测记录的加速度吻合度及识别精度还是较高的。 图9 S0工况模拟加速度与观测加速度对比 图10 S4工况模拟加速度与观测加速度对比 本文通过修改先验分布与似然函数的方法对贝叶斯理论嵌套抽样进行改进,给出了基于加速度时程响应的结构物理参数识别方法,并分别对数值模型和实际振动台试验结构模型进行物理参数识别。得到结论如下: (1) 相较于MCMC抽样方法,嵌套抽样能很好地解决结构物理参数识别中的高维后验联合概率密度函数问题,即使噪声水平较高,也能精确的识别出结构物理参数。 (2) 通过对结构数值模型结构物理参数抽样来看,从抽样进程可以看出该方法十分高效与可靠,从识别结果来看也具有很好的抗噪性。 (3) 通过对实际振动台试验结构模型的识别结果显示,方法可以有效识别实际结构的物理参数,表明方法可以用在实际工程的结构损伤识别之中。 本文只是对低幅值白噪声激励下的结构物理参数刚度及模态参数阻尼比进行了识别,实际结构在较大荷载(如地震)作用下,往往会发生非线性反应,后续工作中将针对这一情况开展进一步研究。
2 结构识别算例
2.1 结构数值模型

2.2 识别结果分析

2.3 与其它方法结果对比
3 振动台RC框架模型参数识别
3.1 振动台试验RC框架模型


3.2 振动台试验RC框架物理参数识别
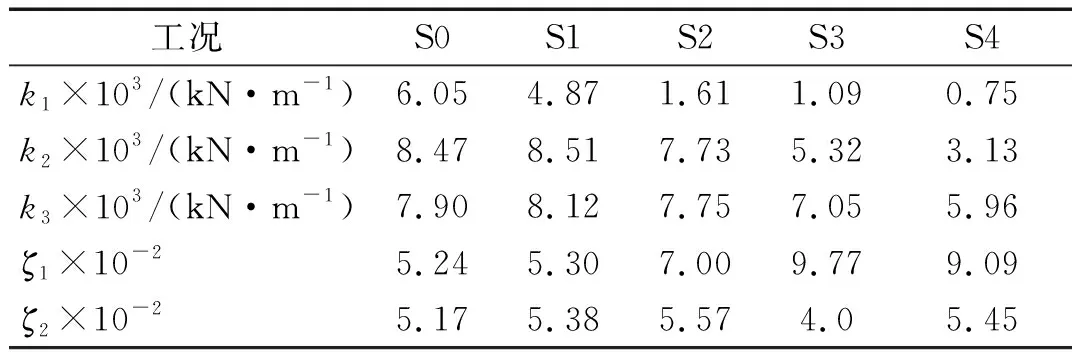
3.3 识别结果分析
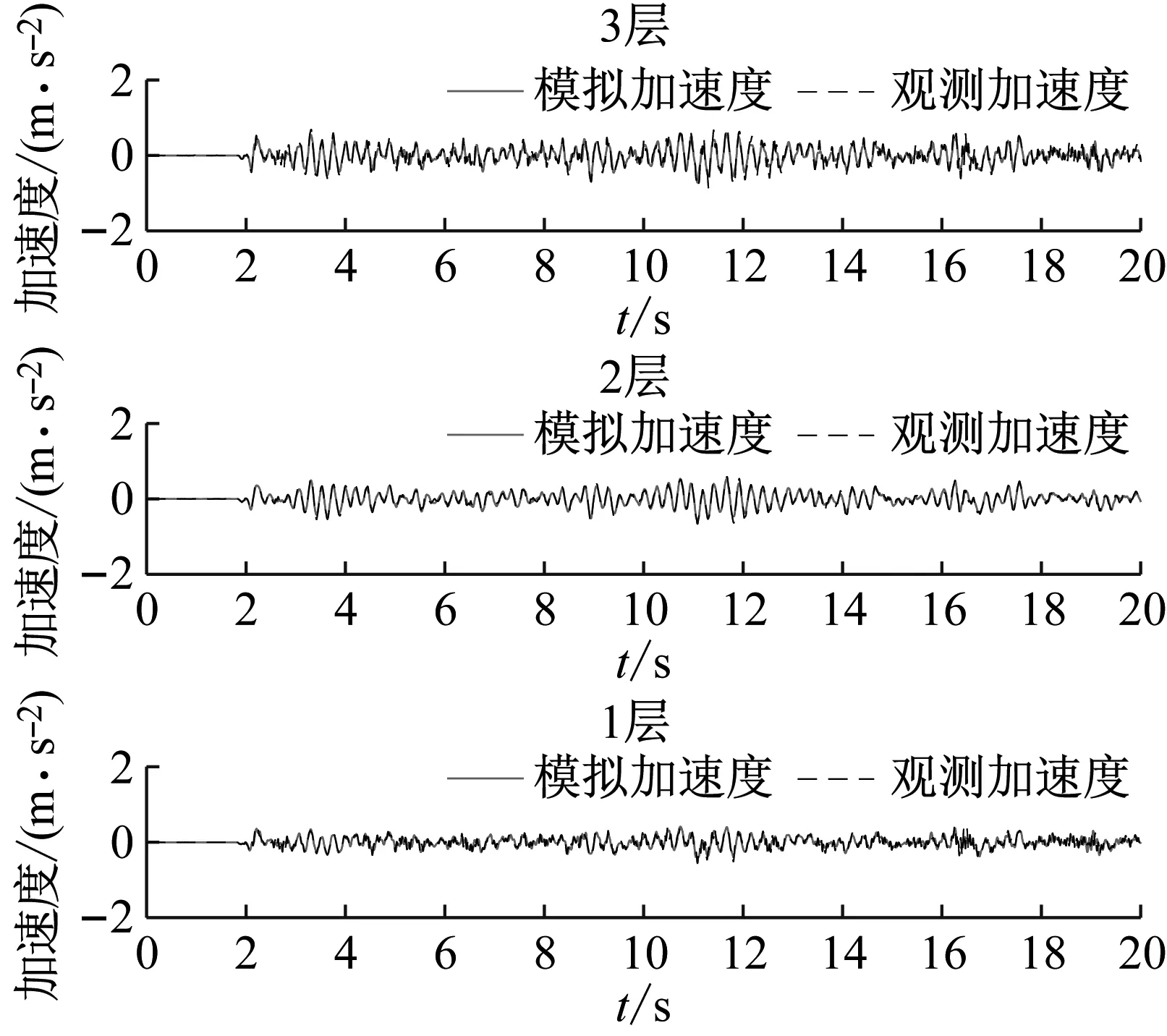
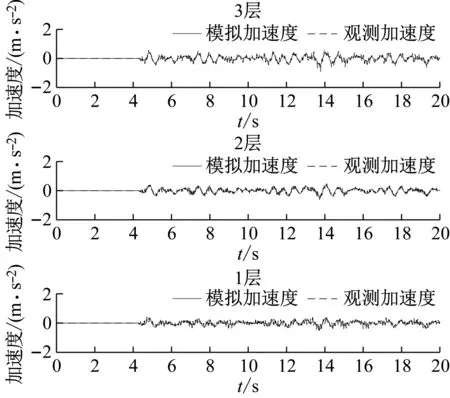
4 结 论

