GH4169合金激光增材制造过程热-力发展数值模拟*

种润， 郭绍庆， 张文扬， 李柏泓， 赵梓钧， 黄帅

(中国航发北京航空材料研究院，北京 100095)

0 前言

镍基高温合金GH4169(美国牌号Inconel 718)在-253～650 ℃范围内可以保持较高的力学性能、高的耐腐蚀性能、高的抗氧化性能、较佳的焊接性能及较高的疲劳性能，因此在航空、航天、石油管道、核工业等领域具有广泛的应用[1]。

增材制造技术，从开发设计模型到制造结构功能部件，彻底改变了传统制造业模式，推动下一代工程设计和创新的出现。增材制造通过降低复杂几何构件的成本并极大提高设计自由度，对许多行业产生了重大影响[2]。但是，激光增材制造过程中复杂的瞬态极速冷热循环过程导致热应力的产生，使零件变形甚至开裂，成为制约激光增材制造技术发展的关键问题[3]。采用试验方法实时测量增材制造过程中变化极快的温度、应力等重要参数十分困难，因此难以对其进行过程监测及控制。另一方面，传统的试验试错方法耗时耗力，而且一种材料、一台设备上得到的经验参数通常不能直接应用到其他材料与设备上，使工艺研发成本进一步升高[4]。

为克服以上困难，研究人员与设备制造商开始探索数值模拟等方法。其中，采用热弹塑性法开展增材制造过程热-力耦合有限元模拟成为当前研究热点之一。热-力耦合分析通过同步计算增材制造过程的温度场与应力场，对温度、残余应力与变形等关键参量进行预测。杜泽林等人[5]研究了成形电流与焊接速度对铝合金应力与变形的影响，发现热输入是影响电弧增材制造应力与变形的关键因素。龚丞等人[6]采用数值模拟研究了316L不锈钢激光增材制造单层沉积工艺参量对残余应力的影响，结果表明，沉积层内沿扫描方向均为拉应力，垂直扫描方向有压应力和拉应力，高度方向残余应力数值较小。沉积层内不同方向的残余应力随激光功率、扫描速率和送粉量变化呈现不同变化特点。赵宇辉等人[7]通过计算验证Inconel 625镍基高温合金激光增材制造时采用单点预热、局部预热、提高环境温度和先分区再连接等4种内应力控制方式的有效性，发现这些方法能够不同程度地降低残余应力、防止变形开裂。张义福等人[8]研究了H13钢薄壁激光增材制造时单向沉积和来回往复沉积2种扫描策略的残余应力，结果表明单向沉积壁残余应力略低于来回往复沉积壁。

由于热弹塑性有限元法计算量大，受计算规模和计算效率限制目前计算仍以薄壁、圆环[9]等简单形状、较小尺寸零件为主，薄壁长度以几十毫米为主。为优化工艺参数、降低其沉积态残余应力，文中针对GH4169合金薄壁零件激光直接沉积，采用MSC Marc有限元软件进行数值模拟，并且通过采取合理选择网格尺寸以及利用对称性等数值模型改进措施，使能够模拟的薄壁零件的长度达到120 mm，高度达到4 mm。

1 有限元模型

1.1 模型假设

增材制造过程影响因素众多，很难全部考虑。因此文中模型中考虑如下简化假设[7,10]：①基板与沉积层材料为各向同性的连续统一体；②材料热、力性能参数随温度变化；③热源简化为高斯模型且保持恒定，忽略穿透效应；④表面对流换热系数简化为常数；⑤基板与沉积层材料服从Von Mises屈服准则，塑性区服从流动准则与硬化准则；⑥忽略沉积过程中的汽化；⑦忽略熔池内流动对温度场、应力场的影响。

1.2 热分析模型

对于密度不变、热容各向同性的物体，热平衡控制方程[11]如下：

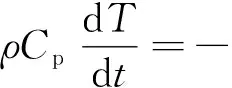
(1)

式中：T为温度；t为时间；∇·为散度；q为热流；r为位置矢量；Q为体热源。

金属体内热量通过热传导传递，以傅里叶定律描述：

qcond=-k∇T

(2)

式中：qcond为热传导热流；k为各向同性热导率；∇为梯度；T为温度。

激光热输入采用高斯面热源模型：

(3)

式中：qin为光斑内任一点输入热流密度；P为激光功率；η为材料对激光的吸收率；r′为激光光斑半径；R为任意点到激光热源中心点的距离。

考虑将对流换热系数与辐射换热系数结合为一个等效换热系数，总热流损失以牛顿定律表示：

q=h(Ts-T∞)

(4)

h=hconv+hrad

(5)

hrad=εσ(Ts+T∞)(Ts2+T∞2)

(6)

式中：h为等效换热系数；Ts为表面温度；T∞为室温，设为25 ℃；hconv为对流换热系数；hrad为辐射换热系数；ε为表面发射率，设为0.3；σ为斯蒂夫玻尔兹曼常数。

1.3 力分析模型

力平衡控制方程为：

∇·σ=0

(7)

σ=Ce

(8)

式中：σ为应力张量；C为四阶刚度矩阵；e为弹性应变张量。

力学计算过程中采用大变形假设。

1.4 材料添加模型

采用Marc软件中自带的“生死单元法”。代表金属沉积区域的单元从分析中删除，仅考虑与激活单元对应的节点自由度。数值分析求解过程只计算激活单元的残差和雅可比行列式，并仅求解激活节点自由度。

与静态单元法相比，生死单元法有如下优点：没有因比例因数引起的错误或矩阵病态；仅对激活单元执行元素残差和雅可比计算；通过牛顿-拉夫森线性化，一次只考虑激活的节点自由度，形成的矩阵规模较小。

生死单元法也有如下缺点：使用用户子程序实现过程较为复杂；每次激活单元时，都必须重新对节点与方程式进行编号，并初始化求解器，这可能会抵消求解较小矩阵的计算优势；激活单元时，连接未激活单元与激活单元的节点可能不在初始温度，引入人为误差。

1.5 依赖温度的材料模型

增材制造过程中材料经历大范围温度变化，随温度变化的材料性能参数对增材制造模拟的准确性非常重要。但是，某些随温度连续变化的材料性能参数，尤其是在高温部分很难准确获得。

基板与沉积材料均为GH4169。查询《中国航空材料手册》[1]得到GH4169合金1 000 ℃以内材料参数，部分高温部分参数参考文献[12]。在手册给出的测量值参数之间线性插值。增材制造过程不会低于室温，低于20 ℃的参数不用外推。高于手册给出最高温度以上软件默认线性外推或平推，文中自定义高温部分材料性能参数。

金属导热机制为电子导热，熔化后的液态金属电子运动更加剧烈，而且液态金属出现后增加了对流换热，因此热导率在熔点附近会有突变。而屈服强度和弹性模量在接近熔点时会降低至零，液相完全没有强度。但计算过程需要材料强度和弹性模量非负以避免刚度矩阵病态问题，因此在接近熔点以及熔点以上设置屈服强度与弹性模量为室温的10%，并假设在此温度区域内金属具有理想塑性。对于其他材料性能参数，超出手册给出的温度范围时都使用最高温度对应的值。计算考虑熔化和凝固的相变潜热。熔点在1 260～1 320 ℃之间，取1 320 ℃为液相线。相变潜热为297.6 J/g。具体参数见表1、表2。

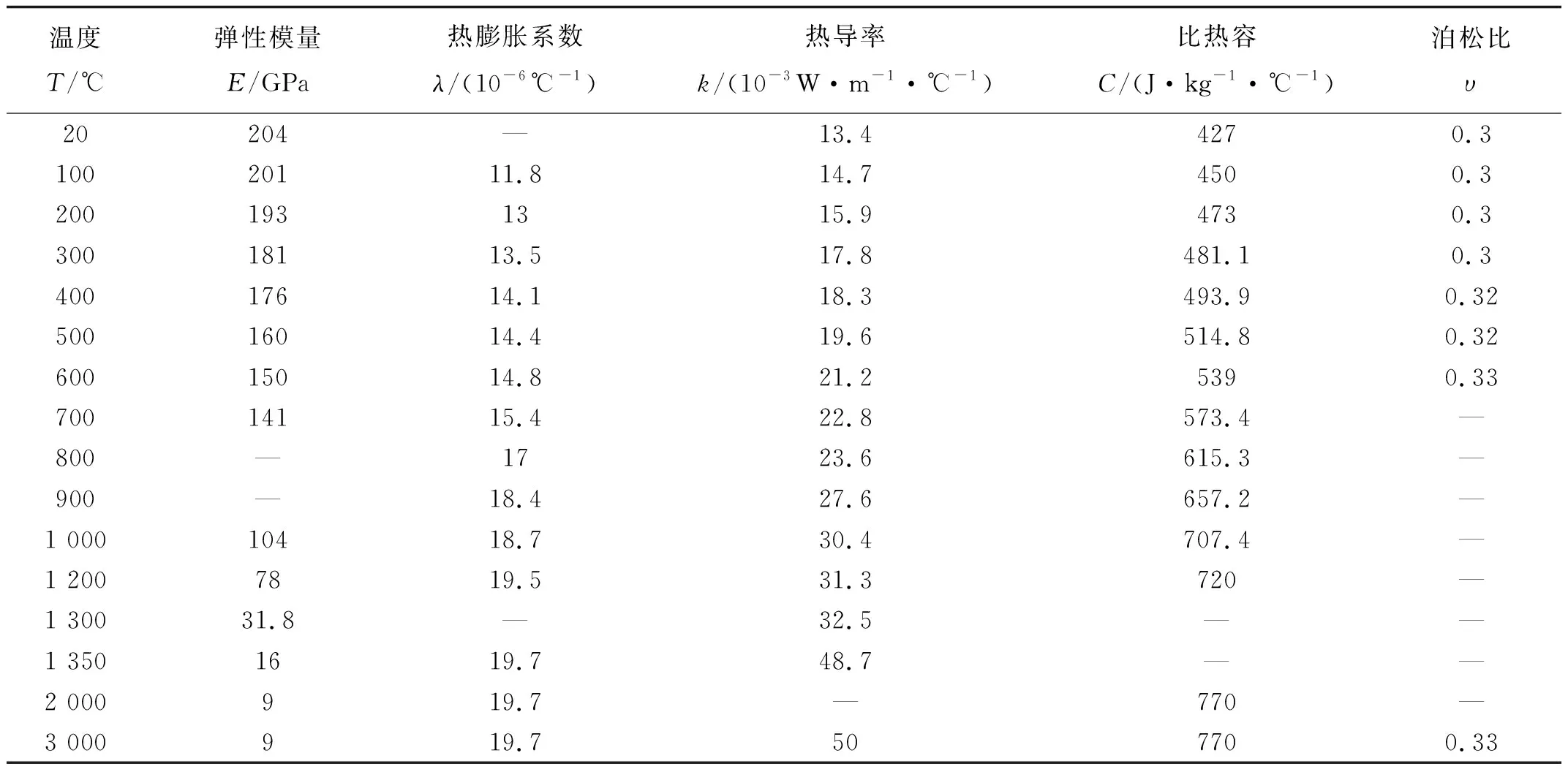
表1 GH4169材料性能

表2 GH4169屈服强度

1.6 有限元模型

沉积基板尺寸为130 mm×50 mm×5mm，沉积层尺寸为120 mm×1.2 mm×4 mm。工艺参数为激光功CM率800 W，光斑直径0.8 mm，单道沉积宽度1.2 mm。扫描速度10 mm/s，沉积20层，每层扫描时间12 s，沉积总时间为240 s。沉积单层层厚0.2 mm，总高度4 mm。单道多层沉积模型具有对称性，为减小计算规模、缩短计算时间取一半模型进行模拟。图1为有限元网格模型。在沉积层及其附近采用小尺寸网格，尺寸为0.2 mm×0.2 mm×0.2 mm。远离沉积层采用大尺寸网格，中间部分过渡网格尺寸。模型中共有72 648个单元，93 300个节点。

图1 网格划分

力学边界条件：基板底部节点x,y,z3个方向的位移约束均设置为0。对称面节点x方向的位移约束设置为0，使其只能在对称面yOz面内移动。热学边界条件为对流和辐射散热，对流换热系数为40 W/(cm2·℃)，表面发射率设为0.3，加载在除对称面外的所有表面。初始温度20 ℃，加载在所有节点上。

载荷工况分段加载，沉积过程共240 s，设为固定时间步长0.02 s。冷却过程7 200 s，采用自适应步长策略。

2 沉积过程数值模拟

2.1 沉积过程温度场

分别选取沉积至第5层中点、沉积第10层中点、沉积第15层中点和沉积第20层中点时刻的温度场分布，如图2所示。图中灰色部分表示超过熔点(1 320 ℃)的熔池，激光加热能熔合之前熔覆的部分，形成冶金结合。在沉积方向前沿温度梯度大，沉积方向后方温度梯度小。整体温度梯度变化剧烈。随着沉积层增加，热量累积明显。在沉积至第20层时刻，光源前方有温度反常高部分。

图2 沉积过程温度场

提取第19层中点到第20层中点的温度场，如图3～图5。激光扫过后，沉积层顶端温度下降最快，高度越低，温度降低越慢。基板上表面形成长椭圆状温度分布。

图3 激光束第19层中点扫描至第20层中点期间的温度场演变(222～225 s)

图4 激光束第19层中点扫描至第20层中点期间的温度场演变(226～229 s)

图5 激光束第19层中点扫描至第20层中点期间的温度场演变(230～233 s)

总体形成温度分布的尖角。总体上，沉积过程中熔池，随着沉积层高度上升，表面积增加，沉积层的散热方式由向基板的传导为主逐渐转变为沉积层表面对流辐射散热为主。

图6为第2,7,12,17层中点沉积过程热循环曲线，热循环曲线峰值温度下降，谷值温度逐渐上升，随沉积过程反复振荡，振幅减小。随沉积层高度增加，热循环曲线峰值温度非线性增加至2 800 ℃以上，说明沉积过程有热累积效应。温度在极短时间内升高并降低，升温降温速率均超过105℃/s。

图6 沉积过程热循环曲线

2.2 沉积过程应力场

分别选取沉积至第5层中点、沉积第10层中点、沉积第15层中点和沉积第20层中点时刻的应力场分布，如图7所示。由图2和图7，激光沉积扫描过的区域因冷却收缩受到约束产生较高的应力。后道沉积时激光扫描到的区域温度再次升高，先释放前道沉积形成的应力，随着温度降低会造成更大的应力。

图7 沉积过程Von Mises应力场

沉积结束时间为240 s。240.06 s温度场中，沉积层与基板连接部分温度异常升高，如图8a所示。同时刻应力场中，同一位置Von Mises应力非常高，如图8b所示。由此可推断，局部区域温度异常升高的原因可能是该部位沉积层降温收缩时受基板约束的力非常大，引起大的塑性应变，使转化为热能的塑性变形功显著增加。

图8 240.6 s温度场与Von Mises应力场

3 沉积结束数值模拟

3.1 残余应力场

冷却7 200 s后的残余应力场分布如图9所示。残余应力主要集中在沉积层上，沿沉积方向的纵向(y向)残余拉应力最大。沉积层两端上方外侧，由于没有约束，可以自由收缩，残余应力较小。垂直于沉积方向的横向(x向)残余应力和高度方向z向残余应力数值较小。基板残余应力水平较低，与沉积层结合部分以残余拉应力为主，其他部分以残余压应力为主。

图9 残余应力场

在基板上表面，与沉积层结合部分有较大压应力。基板纵向两端有部分y向残余压应力和z向残余压应力分布，横向远离沉积层有部分x向和z向残余压应力分布。

中截面残余应力场分布如图10所示。较大的残余应力集中在沉积层，以y向残余拉应力为主。沿深度方向，沉积层与基板连接处均为拉应力，基板向下部分有残余拉应力。基板底面沿y向为残余拉应力，x向与z向均为残余压应力。

图10 中截面残余应力场

3.2 不同路径残余应力

文献[6,8,13]中选取薄壁墙对称路径上的应力分布。但由应力云图，应力最大最容易变形甚至开裂的区域是沉积层与基板连接的部分。因此，文中选取沉积层与基板相交的路径和沉积层棱边进行分析，示意图如图11所示。

图11 选取路径示意图

图12为不同路径的残余应力分布。如图12a所示，沿ab0路径，y方向残余应力在沉积层和基板连接部分(0 mm到0.6 mm)是拉应力，沿路径ab0先快速降低，再逐渐降低，到远端部分(大于3 mm)为较小残余拉应力。x方向和z方向残余应力几乎全是拉应力，沉积层与基板连接部分应力水平高。由图12b，沿ab1路径，y方向残余应力在沉积层和基板连接部分是拉应力，沿路径ab1逐渐降低至0，远端部分有较小残余压应力。x方向和z方向残余应力几乎全是拉应力，沉积层与基板连接部分应力水平高。由图12c，沿ab2路径，3个应力分量变化趋势相似，在沉积层与基板连接部分有极高压应力，应力沿ab2先急速下降至0，再转变为拉应力急速升高，随后逐渐下降至0。沿路径ab0、路径ab1和路径ab2应力分布情况有较大差异。

由图12d和图12e，应力沿路径cd1与路径cd2分布情况类似，x方向与y方向应力水平较高，在沉积层与基板连接处变化幅度剧烈。3个应力分量在基板内部(-5～0 mm)内以拉应力为主，在沉积层(0～4 mm)棱边上以压应力为主。这是因为冷却过程中收缩，棱边没有约束，自由向内变形。

由图12f，沿路径ef，Von Mises等效应力在基板两端较小，在沉积层上迅速上升至700 MPa以上。随着层数上升，薄壁墙两端低应力区逐渐增大。

图12 不同路径的残余应力分布

4 结论

(1)GH4169合金单道20层激光增材制造沉积，随层数和热量累积的增加，通过内部的热传导散热速度降低，沉积层越高部分通过表面的对流和辐射散热越快。

(2)各沉积层经历自身沉积及后续沉积的加热冷却快速热循环，且其温度变化幅度依次减小；随沉积层数增加，沉积热循环峰值温度增加且趋于稳定。

(3)墙体完全冷却后，沉积层整体以残余拉应力为主，y方向应力分量最大。薄壁墙两端上方不受约束，应力水平较低。基板应力水平较低。