岸桥作业对船舶稳性的影响机理及岸桥调度优化

王怀奇，咸富山，牟 爽

（大连海事大学 交通运输工程学院，辽宁 大连 116000）

0 引言

集装箱船大型化对集装箱码头装卸船作业安全提出了新的挑战，如何在兼顾在港集装箱船稳性的基础上优化岸桥调度，提高装卸船作业效率是港方和船方共同关注的问题。船舶进港前，根据船舶航次订舱及集装箱实际集港情况，考虑集装箱属性及其堆积负荷，编制集装箱配积载图。船舶到港后，岸桥根据配积载图装卸船，要求装卸过程中船舶纵稳性和横稳性都处于规定范围之内。合理调度岸桥以降低船舶在港时间是码头追求的重要目标。

针对岸桥调度问题，Daganzo首先对这一问题展开了研究，其对小、大规模算例分别运用精确算法和启发式算法进行求解，目标是减少船期延误的总费用，但其研究没有考虑到岸桥干扰约束，因此难以应用于现实。Kim，等考虑了岸桥间干扰以及任务间的优先关系等约束，并针对小、大规模算例分别运用分支定界法和贪婪随机自适应搜索算法进行了求解。Sammarra，等把岸桥调度问题分解成了路径问题和调度问题，并设计了禁忌搜索算法进行求解。Chuang，等提出了一种改进遗传算法。Izquierdo，等提出了一种基于局部搜索的混合分布估计算法对岸桥调度问题进行求解。范志强分析了以集装箱组为任务对象的QCSP与以整贝为任务对象的QCSP的异同，设计了遗传算法求解以集装箱组为任务对象的岸桥调度模型。丁玲，等建立了一个多目标整数规划模型，目的是在最小化任务的最大完工时间的同时，尽量减少岸桥的移动时间和等待时间，并设计启发式算法进行求解。张思，等针对操作时间不确定性条件下的岸桥调度问题建立了混合整数随机规划模型，并设计了粒子群算法和禁忌搜索算法进行求解。

为了使岸桥调度问题的模型更符合实际情况，部分学者考虑了装卸过程中船舶的状态。Al-Dhaheri，等建立了MIP模型并设计了改进的遗传算法对带有船舶稳性约束的岸桥调度模型进行求解。Chen，等建立了三个最大完工时间约束模型，借此获得风险规避解，降低船舶的不稳性以及解不可行的影响。Wu，等研究了带有吃水和吃水差约束的岸桥调度问题，建立了带有吃水和吃水差约束的岸桥调度模型，并运用分支定界法和混合遗传算法进行求解。Msakni，等应用一种两阶段方法求解带有船舶稳性约束的岸桥调度问题，在第一阶段中使用列生成法求解了没有船舶稳性约束的岸桥调度问题，在第二阶段中调整获得的调度方案，使其符合船舶稳性要求。

综上所述，现有针对岸桥调度优化问题的研究大部分未考虑船舶稳性的要求，且部分关于稳性约束的研究中仅考虑了集装箱船重心偏离中轴线的距离，忽略了集装箱船的横向稳性要求，缺少有关集装箱装卸过程中岸桥调度对船舶稳性影响的机理研究。故本文提出岸桥装卸集装箱对船舶稳性的影响机理，考虑装卸过程中船舶横向稳性和纵向稳性要求，同时考虑岸桥间的不可跨越与安全距离约束，以最小化最大岸桥完工时间为目标，构建岸桥调度优化模型，并设计改进遗传算法对模型进行求解。

1 集装箱装卸作业对船舶稳性的影响机理

由于岸桥是轨道式设备，其在作业时不同岸桥间不可交叉跨越，而且要保持一定的距离以保证作业安全，经典岸桥调度问题就是在保证上述约束的前提下给每个岸桥分配最合理的作业顺序，以尽可能缩短船舶在港作业时间。但在岸桥装卸过程中，集装箱船的稳性也是同样需要保证的，在此，针对船舶稳性特征，讨论了集装箱的放置与提取对船舶纵稳性和横稳性的影响机理，如图1所示，并利用举例的方式说明多岸桥同时装卸集装箱时对船舶稳性的影响程度。

假设待装卸集装箱船在入港时是平衡状态，也就是其左右以及前后积载集装箱的数量相同，此时每个集装箱的装载或卸载都会影响到集装箱船的平衡状态，故当时船舶的横倾以及纵倾力矩可以表示为岸桥左右/前后装卸集装箱产生的力矩，也就是本文中设计的不稳定值概念。本文左右不稳定值的计算方式为集装箱船纵向中轴线左侧装卸载集装箱与各箱相对纵向中轴线距离相乘得到的力矩加上用同样方法得到的右侧装卸载集装箱对于纵向中轴线的力矩，例如图1中正在进行作业的集装箱船，有两台岸桥对该集装箱船同时进行装卸，假设单个集装箱的重量为，Ω为在时刻已完成集装箱组任务的集合，为集装箱组任务中所有集装箱的集合，为作业系数，装船为1，卸船为-1，为集装箱所在列位号，为集装箱船纵向中轴线向集装箱船左舷以及右舷方向的第1个列位离纵向中轴线的距离，因此在时刻图1中集装箱船的左右不稳定值为：

图1 岸桥装卸过程对船舶稳性的影响机理

其中，当为偶数时，/2；当为奇数时，(+1)2。

本文前后不稳定值的计算方式为集装箱船横向中轴线船头一方装卸集装箱的数量与各集装箱相对横向中轴线距离相乘得到的力矩加上用同样方法得到的船尾侧装卸集装箱对于横向中轴线的力矩，Num为集装箱组任务中所包含集装箱的数量，为集装箱组任务所在贝位号，为集装箱船横向中轴线向船头以及船尾方向的第1个贝位离横向中轴线的距离，因此在时刻图1中集装箱船的前后不稳定值为：

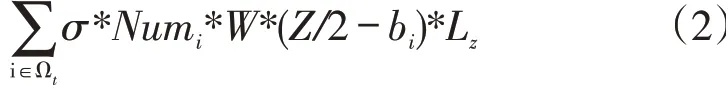
其中，当集装箱船总贝位数为偶数时，2；当为奇数时，1。

2 数学模型

2.1 模型假设

建立起考虑集装箱船稳性的岸桥调度模型，假设：

（1）定义一个集装箱组为一个任务；

（2）岸桥数量以及到港船舶的装卸任务量已知；

（3）岸桥在贝位间的移动时间不可忽略；

（4）集装箱尺寸均为20ft，货物类型相同，不考虑特殊集装箱。

2.2 参数及符号

：岸桥编号，按贝位递增顺序编号，12；

：集装箱组任务编号，按贝位递增顺序编号，12；

：任务所在贝位；

：岸桥作业单个集装箱需要的时间；

：岸桥作业任务需要的时间，=Num*t；

：任务所在位置（用贝位号表示）；

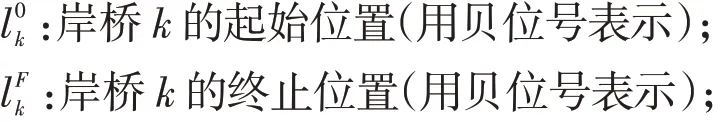
：一个足够大的常数；

：岸桥在相邻两个贝位之间移动所需时间；

：岸桥从任务所在位置移动到任务所在位置所需时间；

：岸桥完成当前任务后进行下一任务前因其他岸桥干扰所产生的等待时间；

：所有岸桥的集合；

Ω：所有任务的集合；

Ψ：不能同时进行作业的任务集合，如果不能同时进行，可以用()∈Ψ表示；

Φ：有先后作业顺序的任务集合，如果任务必须先于任务完成，则可用()∈Φ表示；

：集装箱船左右、前后不平衡值阈值；

Ω：任务中所有集装箱的集合；

Ω：任务开始时刻已完成任务的集合；

Ω：任务结束时刻已完成任务的集合；

Num：任务装载/卸载集装箱的数量；

Num：集装箱船贝位所能装载的最大集装箱数量；

Num：集装箱船列所能装载的最大集装箱数量。

决策变量：

成时刻，z=1；否则z=0。

2.3 模型建立

本文中建立的考虑集装箱船稳性的岸桥调度模型是Kim，等建立的模型的扩展。

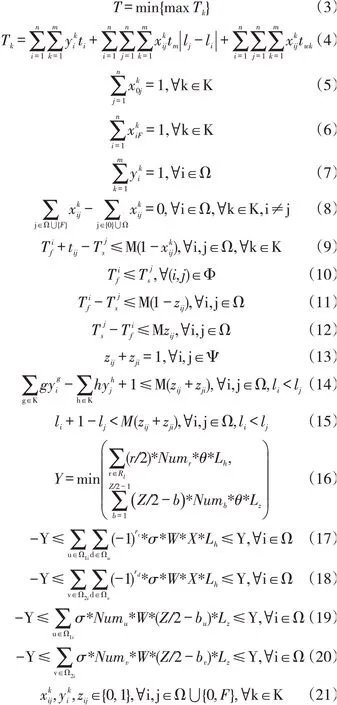
式（3）表示最小化岸桥最大完工时刻。式（4）定义了岸桥的完工时刻，表示岸桥作业的所有任务的作业时间、岸桥移动时间以及因干扰产生的等待时间之和。式（5）表示每个岸桥只能选择一个任务作为其起始任务。式（6）表示每个岸桥只能选择一个任务作为其结束任务。式（7）表示一个任务只能由一个岸桥作业。式（8）确保流量平衡并确定每个任务的先后顺序。式（9）考虑到岸桥的移动时间以及等待时间，表示任务顺序与时间的关系，从而避免子回路的产生。式（10）表示任务间的优先关系。式（11）和（12）表示如果任务在任务之后作业，则任务的开始时刻要大于等于任务的完成时刻。式（13）表示任务非同时进行约束，即同一贝位里的多个任务不能同时由同一岸桥作业。式（14）保证岸桥之间不发生交叉，即当任务在作业时间段上有重叠时，对应的作业岸桥不能相互穿越，当任务(＜l)在作业时间段上有重叠时，+z=0，因假设岸桥编号与贝位编号均沿同一方向由小到大，如果岸桥作业任务，岸桥作业任务，则1≤h，即岸桥不可相互穿越作业。式（15）表示当任务在作业时间段上有重叠时，这两个正在作业的任务必须间隔一个贝位，也就是分别作业这两个任务的两个岸桥保持一个贝位的安全距离。式（16）为本研究中的集装箱船左右、前后不稳定值阈值的计算方法，它的取值为集装箱船前部装满/左部装满产生的不稳定值乘以敏感系数中较小的那个。表示位于集装箱船左部列的集合，={ }

24。式（17）和（18）表示集装箱船左右不稳定值约束，即保证每一任务开始及结束时刻集装箱船的左右不稳定值都处于阈值范围内。式（19）和（20）表示集装箱船前后不稳定值约束，即保证每一任务开始及结束时刻集装箱船的前后不稳定值都处于阈值范围内。式（21）表示决策变量的取值范围。

3 算法设计

由于岸桥调度问题已被证明是NP-hard问题，而且本文模型相对于其他单纯的岸桥调度问题增加了集装箱船的稳性约束，模型求解将更加复杂。故本文使用自适应遗传算法进行模型求解。

3.1 染色体的表示

染色体的长度由集装箱船的任务总数决定。每条染色体用1~的整数随机排序产生的序列来表示，如图2所示。

图2 染色体示意图

3.2 染色体验证

由于初始产生的染色体有一定概率违背任务优先关系约束，这些不满足任务优先关系约束的染色体，也就是问题的无效方案，必须采取修复措施对其进行修复，使其成为可行方案。

在集装箱船的装卸过程中，同贝位的卸船任务必须先于装船任务完成，舱内的装船任务要先于甲板装船任务，甲板的卸船任务要先于舱内卸船任务。如果随机产生的染色体违反了上述任务优先关系约束，比如在图3所示的染色体中，任务4、任务5及任务6属于同一贝位，任务4为甲板卸船任务，任务5为舱内卸船任务，任务6为舱内装船任务，它们的优先关系为“4-5-6”，所以按照图3的原始方案是不可行的，为了使其可行，将其按照任务优先关系进行修复，如图3所示。

图3 违反任务优先关系约束的染色体修复过程

3.3 适应度值计算

在上一节进行了染色体的修复后，得到了满足任务优先关系的种群，因此可在本节进行染色体的解码操作，从而得到满足第二章约束的岸桥调度方案，本文中对集装箱船稳性约束的处理方法为罚函数法，具体方法如下：

在每个任务开始和完成的时刻计算集装箱船的左右不稳定值和前后不稳定值，然后将其与不稳定值阈值比较，如果发现在某个时刻超出阈值，则记录那个时刻的左右不稳定值或前后不稳定值与阈值的差值，并把累计的这些差值分别记做与。本文的目标函数是最小化最大岸桥完工时间，把和作为惩罚时间加入到最大岸桥完工时间里，故本文的适应度函数可以表示为：

，为惩罚系数。

3.4 选择

本文使用轮盘赌法进行选择，根据各个染色体的适应度值来确定其被选择的概率。令表示种群中第个染色体的适应度值，令∑表示种群的适应度值总和，种群规模为，则个体对应的概率为：

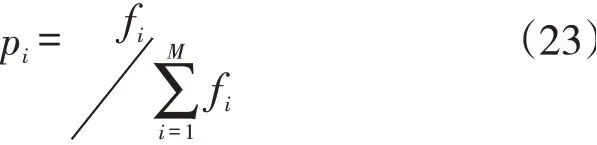
3.5 交叉

本文使用顺序交叉方式，交叉过程如图4所示。（1）从种群中随机选取两个父代染色体，并随机选取它们的一个基因片段。将父代1的基因片段复制到子代1的对应位置后，把父代2中与子代1相同的基因删除后依次填充到子代1的剩余位置；（2）将父代2对应的基因片段复制到子代2后，把父代1中与子代2相同的基因删除后依次填充到子代2的剩余位置。

图4 顺序交叉过程

本研究中交叉操作的交叉概率参考了文献[14]，具体方法如下：

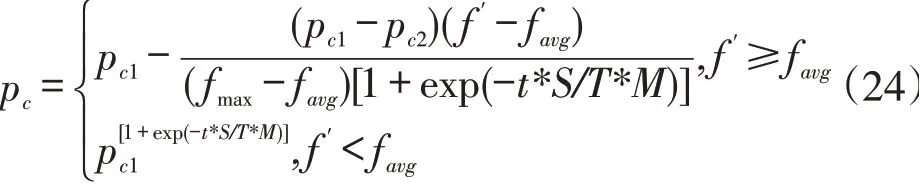
其中f是两个交叉个体中适应度较大个体的适应度值，是每代种群中最大的适应度值，是每代种群中适应度的平均值，为当前进化代数，是进化过程中最优解没有改变的个体数目，是最大迭代代数，是种群大小。

3.6 变异

为避免遗传算法陷入局部最优，本文选用互换变异（SWAP）的变异方法，即随机交换染色体中两个不同基因的位置，变异过程如图5所示。

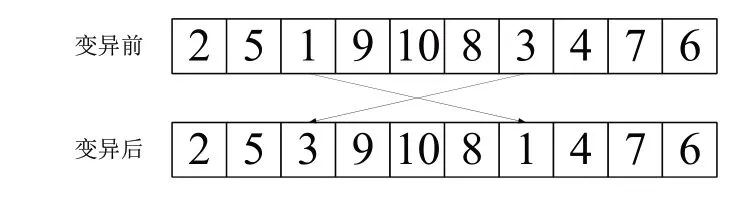
图5 变异过程

本研究中的变异概率由式（25）计算：

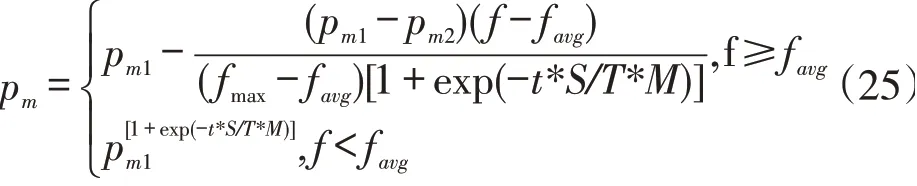
其中是要变异个体的适应度值，、、、、、均与式（24）中的含义相同。

4 算法验证与算例分析

4.1 小规模算例

为验证本文提出的遗传算法的有效性，先对一只最大载箱量为1 000 TEU的集装箱船进行实验，该待作业集装箱船的各任务如图6所示，以证明本文提出的算法能够有效求解带有集装箱船稳性约束的岸桥调度模型。

图6 待作业集装箱船

算例中共有12个待装卸贝位，共计16个任务，为其作业的岸桥数量为3台，计算出各个任务所产生的左右不稳定值、前后不稳定值列在表1中，根据上文提到的阈值计算公式，该集装箱船的左右、前后不稳定值阈值约为100，岸桥移动一个贝位的时间为1min，作业一个集装箱的时间为2min。

表1 岸桥作业各任务产生的的不稳定值

表1中与分别表示岸桥作业各个集装箱组所产生的左右、前后不稳定值，采用Matlab 2016进行编程求解，如图7所示，算法在150代左右找到了一个最优的调度方案，此最优调度方案如图8所示，岸桥最大完工时间为284min，同时从图9中可以看出，在整个调度过程中，只有在第4个任务结束的时刻集装箱船的左右不平衡值以及第2个任务结束的时刻集装箱船的前后不平衡值超过了规定的阈值（、、、分别表示该任务开始时刻的、值以及该任务结束时刻的、值），当时的前后不稳定值以及左右不稳定值分别为-104，-110，故整个调度方案的与值分别为4、10，由此可见在整个岸桥作业过程中，超出左右、前后不稳定值阈值的时刻以及超出的范围都是非常少的，验证了本文设计的考虑稳性的遗传算法的有效性。

图7 算法迭代图

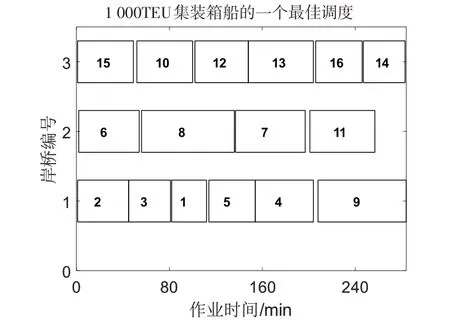
图8 岸桥作业甘特图

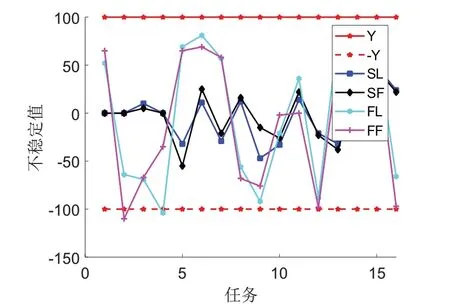
图9 各任务开始及结束时刻集装箱船的左右、前后不稳定值

4.2 对比分析

为了进一步说明本文算法的可应用性，本节对考虑集装箱船稳性约束和忽略稳性约束的岸桥调度求解结果进行对比分析。主要分析了船舶稳性约束在具体算例背景下对求解效果的影响，包括：（1）加入船舶稳性约束会对岸桥最大完工时间产生什么样的影响；（2）加入船舶稳性约束后船舶的左右、前后不稳定值减少了多少，也就是安全性提高了多少。根据集装箱船实际规模生成六个不同规模的集装箱船算例，各个实验中集装箱船各任务产生的左右、前后不稳定值都是根据每个集装箱船的规模在一定范围内随机生成，实验结果见表2，表中所有的、、都是运行相应算例十次之后取得的平均值。

表2 不同规模下考虑稳性约束与忽略稳性约束算法对比

表2中，表示各个实验规模下集装箱船的左右、前后不稳定值阈值，1、1、1分别表示考虑稳性情况下岸桥的最大完工时间、总的左右不稳定值差值以及总的前后不稳定值差值，2、2、2分别表示不考虑稳性情况下岸桥的最大完工时间、总的左右不稳定值差值以及总的前后不稳定值差值。

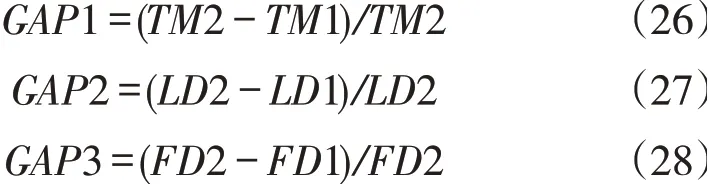
式（26）-（28）分别表示考虑稳性情况下与忽略稳性情况下岸桥最大完工时间的差距以及总左右、前后不稳定值差值的差距。

实验结果表明，若不考虑集装箱船稳性约束，、值会随着算例规模的增大而大幅增加，但在考虑集装箱船稳性的情况下，集装箱船的、值的变化不是很明显，并且可以在每个情景下都保持较低的水平；同时，两种情况下岸桥最大完工时间的值可以保持在-6%以下。以上结果表明，本文算法可以在牺牲少部分岸桥完工时间的情况下大幅降低集装箱船的不稳定值，做到了对岸桥完工时间以及集装箱船稳性的同时优化，提高了集装箱船在码头装卸期间的安全性。同时，在本节实验过程中发现在忽略稳性约束的情况下，最大岸桥完工时间相同的两个调度方案，它们的与值可能相差特别大，而在考虑稳性的情况下，每一调度方案都能得到较小的与值，这一发现提醒我们在码头作业过程中不能一味追求作业效率，在作业过程中的安全性同样不能忽视。

4.3 敏感性分析

由式（14）可以看出，本文中的敏感系数对集装箱船的左右、前后不稳定值阈值有较大的影响，若敏感系数过大，则阈值过高，这将不能对集装箱船的稳性起到很好的约束作用；若敏感系数过小，则阈值过低，导致在考虑稳性的情况下也会存在较高的、值，这并不是本文所希望看到的。因此对的取值进行敏感性分析，取4.1节最大载箱量为1 000 TEU的集装箱船进行实验，其前部/左侧装满产生的不稳定值约为500，分别乘以不同的敏感系数，得到的阈值以及各个实验的结果见表3。

表3 敏感系数θ对集装箱船不稳定值的影响

从表3可以看到，在敏感系数大于0.2的实验中（实验4、5），考虑集装箱船稳性下的、值都为0，不能与忽略稳性的情况形成一个很好的对比，而在敏感系数小于0.2的实验中（实验1、2），、值都处于一个较高的水平，有违本文中对稳性进行约束的目的，故本文在敏感系数为0.2的条件下对考虑集装箱船稳性的岸桥调度问题进行研究。

5 结语

本文对自动化集装箱码头单船岸桥调度问题进行了研究，在考虑集装箱组间的优先关系、岸桥间的干扰约束的前提下，将集装箱船的稳性约束纳入到岸桥调度问题中，针对此问题建立了考虑集装箱船稳性的岸桥调度模型，并设计了GA算法对其求解。算例分析结果表明：本文模型及算法所求出的岸桥调度方案在优化了岸桥最大完工时间的前提下，在岸桥调度过程中产生的左右、前后不稳定值也大幅减少，极大地提高了作业过程中的安全性。但本文还存在一些不足，仅研究了单船的岸桥调度问题，接下来可研究考虑整个码头作业过程中稳性的多艘船舶的岸桥调度优化问题；同时随着各种智能算法被应用到自动化码头这一领域，应用其他高效的智能算法优化岸桥调度方案将作为未来的研究方向。