热力耦合作用下碳质千枚岩强度演化规律分析

杨丙昌

(中铁十四局集团第五工程有限公司,山东兖州 272100)

地温(热) 与地应力(力) 是影响变质岩区域深埋软岩隧洞掘进过程与安全管理的重要因素。西南山区条件复杂多变,地层岩性受地质构造控制,川藏铁路、南水北调西线及各类水利枢纽等基础工程在修建过程中常需穿越高地温的深埋变质岩体区域[1],如新疆公格尔水电站引水洞石墨片岩地温维持50◦C～70◦C,云南贡嘎隧道千枚岩地温达45◦C,黑白水电站引水洞页岩地温达57◦C 等。四川毛尔盖水电站引水洞地处高地温大埋深的碳质千枚岩地层,隧洞开挖诱发了围岩应力重分布,加之因掘进作业降温的温差效应,加剧了断面收缩、衬砌开裂及顶板坍塌等大变形灾害发生频度,影响了掘进过程岩体受力特性评判、围岩稳定性评价与施工安全管理,亟待查明热力耦合作用下碳质千枚岩强度演化规律。

热力作用下围岩体强度演化规律成为了岩石工程中备受关注的研究方向之一。李天斌等[2]通过模型试验发现了地温变化诱发了围岩附加温度应力,增大了其脆性破坏概率；陈子全等[3]从能量耗散角度得出了碳质千枚岩强度与塑性随围压增加而增强,其破坏形式从压致拉裂转为剪切滑移；孟召平等[4]采用单因素分析法用影响系数分别量化温度场与应力场对砂岩强度影响。孟陆波等[5]定性指出了应力场是软岩隧洞大变形的主要因素,温度场对围岩强度存在初始热损伤作用；朱珍德等[6]建立了大理岩热力耦合作用下细微观模型,指出温度变化下热应力引起了细观裂纹发育,强度随温度升高而降低；严健等[7]指出热力耦合作用下隧道通风降低了岩体温度,同时诱导了围岩板裂化结构面,呈剪切断裂型破坏形式。朱振南等[8]引入正态分布,采用Mohr–Coulomb强度准则(M–C 准则) 量化温度场对岩石统计热损伤效应,高玮等[9]依据Weibull 分布和Heok–Brown强度准则(H–B 准则) 探讨了不同围压下破裂岩体强度特性。Drucker–Prager 准则、非线性M–C 准则、Bieniawski 幂函数准则、指数强度准则等强度理论及其改进形式也用于描述多因素作用下岩体强度变化规律[10-11]；其中,依据大量试验数据所建立的M–C 准则与H–B 准则仍为工程设计与施工人员所广泛使用的强度理论。

隧道围岩体强度演化是多种因素共同影响的体现,当前对热力耦合作用下软岩的强度变化规律的研究还较少,能够有效指导工程现场建设的资料仍然不足。为此,依据室内试验结果,分析了温度场与应力场对碳质千枚岩应力应变曲线影响；基于M–C 准则与H–B 准则分别建立热力耦合作用下碳质千枚岩强度演化计算方法,即Mohr–Coulomb–Thermal(M–C–T) 法和Heok–Brown–Thermal (H–B–T)法,并对比分析两者间误差,为软岩区隧洞掘进与支护施工建设给予参考。

1 热力耦合室内试验

四川西部某大(2) 型水电站枢纽布置圆形有压引水隧洞,其平均埋深为400 m,最大埋深超过1000 m；地层以黑色碳质千枚岩为主,实测最高地温达47.2◦C。室内试验所用岩样为现场钻孔岩芯,经X 射线衍射图谱(见图1) 分析,岩样主要成分为黑云母68%,伊利石18%,石英10%,膨胀性不显著。

图1 岩样X 射线图谱Fig.1 X-ray atlas of rock samples

采用自带温控设备与数据采集系统的MTS815程控伺服岩石力学试验机进行热力耦合的单轴和常规三轴试验,设定温度与应力2 因素4 水平共计16 组试验,测定碳质千枚岩在热力耦合下应力应变曲线与峰值强度分布。根据引水隧洞埋深,设定0 MPa,10 MPa,20 MPa 与30 MPa 四种工况静水压力(σ3),载荷施加速率为0.005 mm/s；考虑施工过程采用冰水混合物对围岩体降温的作法,设定试验温度(T) 为0◦C,20◦C,40◦C 与60◦C 四个等级,温度施加速率为1.0◦C/min。试样尺寸为直径50±0.5 mm,高100±0.5 mm 的圆柱体,试验过程为：(1) 先将环境设定为20◦C (常温),放置试样；(2) 施加静水压力至预定值,并保持2 h；(3) 调节温度至预定值,并保持恒温5 h；(4) 施加轴向载荷直至试样破坏。

2 热力耦合作用分析

2.1 应力−应变曲线

整理试验结果,在同一坐标系下绘制各温度−围压影响下试样的偏应力(σ1−σ3) 随应变ε(轴向应变ε1,侧向应变ε3与体积应变εv)曲线,见图2。从图2 可知,依据峰值应力前后曲线性态,将热力耦合作用下碳质千枚岩(σ1−σ3)–ε曲线大致分为脆性破坏与延性破坏两类[12]。

图2 碳质千枚岩应力−应变曲线Fig.2 Stress-strain curves of carbonaceous phyllite

(1) 脆性破坏曲线。随着轴向载荷增加,试样发生弹性变形,(σ1−σ3) 与ε均呈线性缓慢增加；当岩石变形进入屈服阶段,ε1持续增大,但ε3增大的幅度大于ε1,εv存在减小的趋势；岩石达到峰值强度后发生破坏,(σ1−σ3) 急剧减小,ε3大于ε1,εv小于0,试样出现了扩容现象,残余强度不显著,如图2(a)中0◦C,20◦C,40◦C 及60◦C 的曲线,图2(b)中0◦C,20◦C 及40◦C 的曲线,图2(c) 和图2(d) 中0◦C 曲线。

(2)延性破坏曲线。峰前曲线形状与脆性破坏相似,峰后曲线(σ1−σ3) 随ε增加呈变化幅度较小或者缓慢跌落,ε3与εv增加的幅度大于ε1,扩容现象较为显著,存在残余强度,如图2(c) 中40◦C 及60◦C 的曲线,图2(d) 中40◦C 及60◦C 的曲线。

从(σ1−σ3)–ε曲线可知,碳质千枚岩在低围压与低温度呈脆性破坏,残余强度不显著；在高围压与温高度作用时呈延性破坏,存在明显的残余强度。两种破坏模式下体积在峰后均增大,出现了显著扩容现象。

2.2 Mohr–Coulomb 强度准则

M–C 强度准则是基于各向同性介质微元体所受剪切应力τ达到其极限应力τmax时发生破坏并逐渐发展演化为整体破坏而建立的计算方法,其表达式为

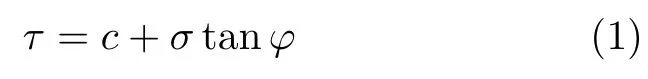
式中,σ为正应力,MPa；c为黏聚力,MPa；φ为内摩擦角,(◦)。

常规三轴条件下根据摩尔圆中角度换算关系,将式(1) 变换为

式中,σf,σ3分别为峰值强度与围压；M,N为系数

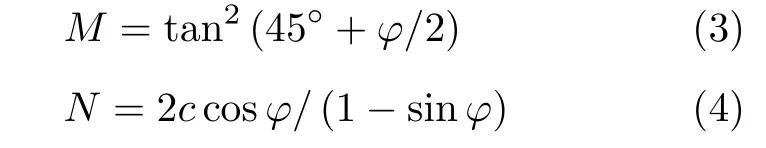
整理图2 中碳质千枚岩单轴与三轴的峰值应力数据,依据式(2) 采用最小二乘法拟合得到系数M与N值,见图3；再利用式(3)与式(4)便求得M–C准则下强度指标c与φ。

图3 M–C–T 法σf −σ3 分布Fig.3 Distribution of σf −σ3 for M–C–T method

从图3 可知,热力耦合作用下碳质千枚岩σf与σ3线性关系显著。为进一步探讨温度场作用,在同一坐标系下绘制c与φ随T的分布,见图4。

从图4 可知,c随T升高呈线性增大,φ的变化规律不明显,仍采用线性与二次函数分别拟合c −T与φ–T分布,见式(5) 与式(6)。

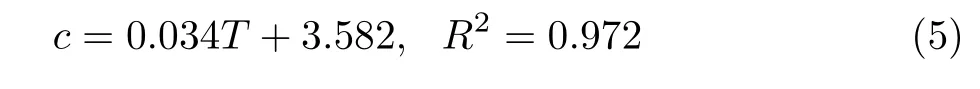
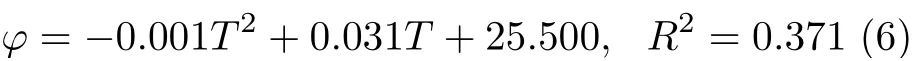
图4 c 与φ 随T 变化曲线Fig.4 Curves of c and φ with T changing

将式(3)～式(6) 代入式(2) 得到基于M–C 准则考虑热力耦合作用下碳质千枚岩破坏强度σf,M−C计算方法,记为M–C–T 法,即

式中φ采用式(6) 计算,若不考虑T对φ影响,φ取25.5◦(即均值)。

2.3 Heok–Brown 强度准则

H–B 准则是根据岩体性质并分析了大量岩体与岩块破坏时试验数据后,总结得到了主应力间关系的经验方程,即

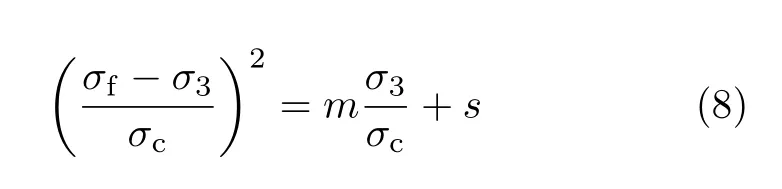
式中,σc为岩块单轴抗压强度；m是与岩石种类有关的参数,s是与岩体结构面性质有关的参数。利用式(8) 整理试验数据时发现(σf−σ3)2/σ2c与σ3/σc之间指数关系更优于线性关系,见图5。

图5 H–B–T 法σf −σ3 分布Fig.5 Distribution of σf −σ3 for H–B–T method

从图5 可知,热力耦合作用下碳质千枚岩强度演化规律可概化为式(9) 形式的数学表达。

式中h与n是温度作用下与岩石种类和岩体结构面性质有关的参数。

整理试验数据,发现不同T和σ3下h变化较小；在H–B 准则中,m表征岩块的强度特征,同一种类岩块,m取值范围较小,则将参数h与m的内涵视为相似,均为与岩石种类相关的参数。因此,此处取1.100 (均值)；σc和n均与T呈显著的线性关系,见图6,得到其拟合表达式为

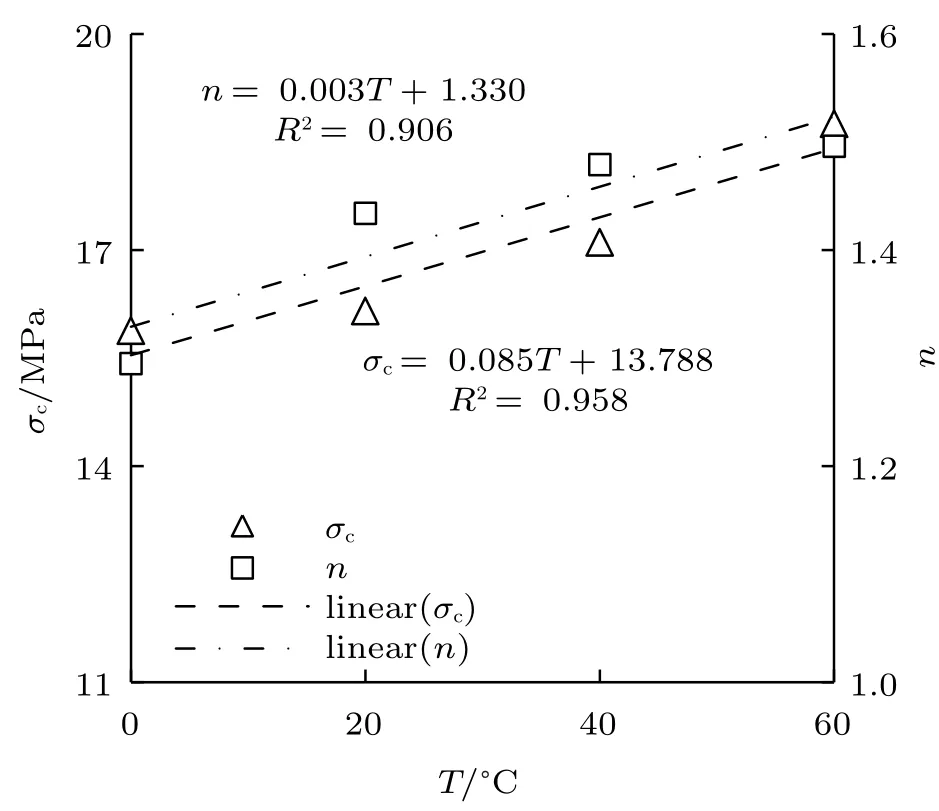
图6 σc 与n 随T 变化曲线Fig.6 Curves of σc and n with T changing

将式(10) 与式(11) 代入式(9) 得到基于H–B准则考虑温度与围压耦合作用下碳质千枚岩破坏强度σf,H−B计算方法,记为H–B–T 法,即

3 计算方法评价

将φ取25.5◦,h= 1.10,再取相同T与σ3采用式(7)和式(12)进行计算,得到σf,M−C与σf,H−B计算值；采用式(13) 分析两种模型与试验值的相对误差Err。图7 为不同工况下热力耦合作用下碳质千枚岩试验值σf,σf,M−C与σf,H−B条形分布图,图8为各自Err在试验值两侧的分布。

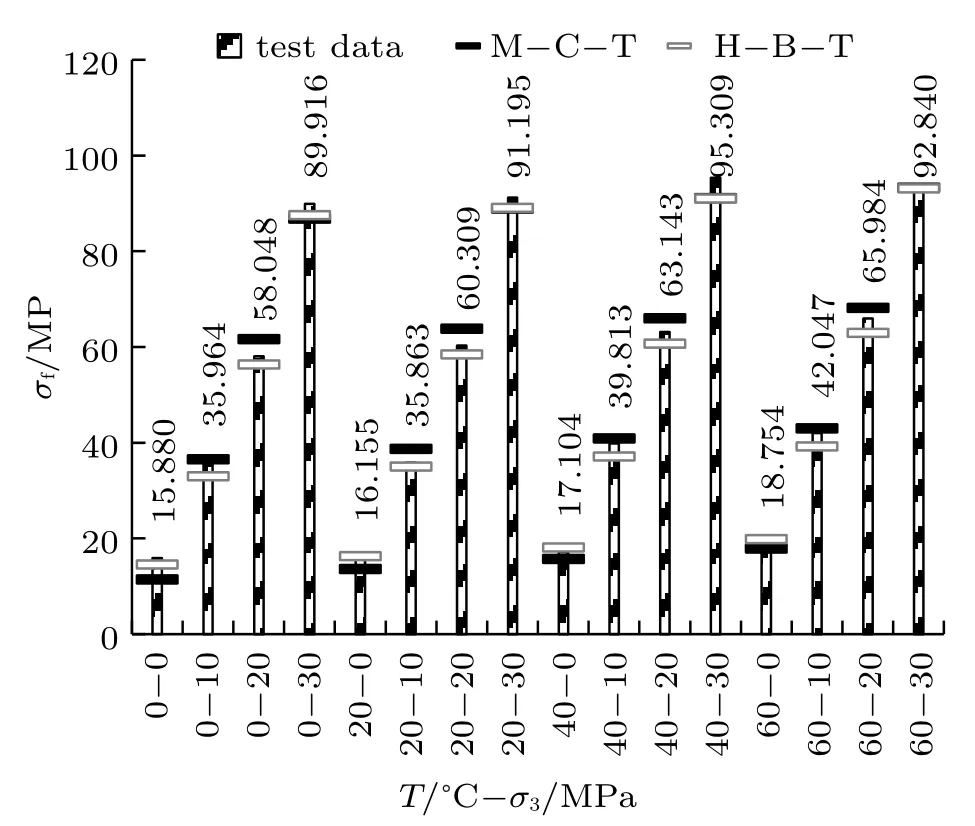
图7 σf,σf,M−C 与σf,H−B 分布Fig.7 Distribution of σf,σf,M−C and σf,H−B

由图7 可知,σf,σf,M−C与σf,H−B三者间数值差异较小,这说明M–C–T 法和H–B–T 法均能较好地量化热力耦合作用下碳质千枚岩强度演化规律；从图8 中Err大小及分布可知,M–C–T 法计算值在试验值两侧均匀分布,计算误差介于−28.5%～7.7%,离散程度较大；H–B–T 法计算值大多均分布于试验值偏小一侧,计算误差介于−8.9%～5.6%,离散程度较小。因此,与M–C–T 法相比,H–B–T 法计算结果稳定性更高,且更偏向于安全。

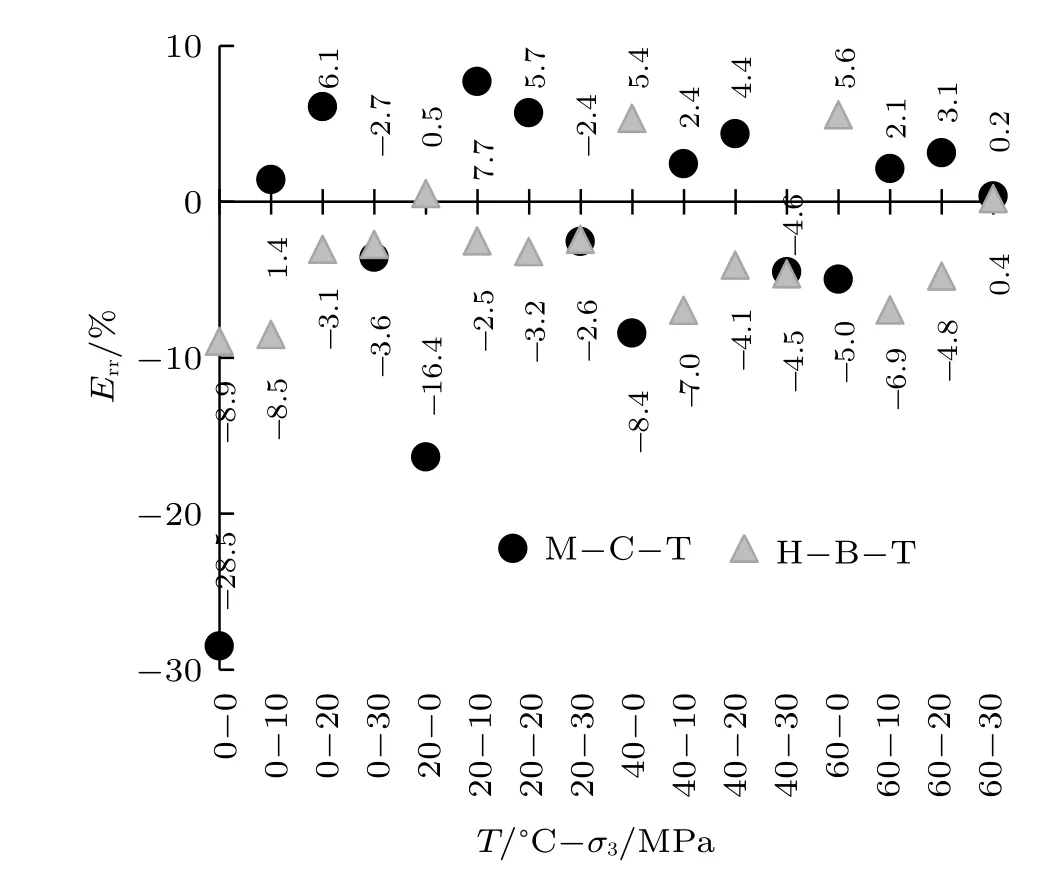
图8 M–C–T 法和H–B–T 法的Err 分布Fig.8 Err distribution of M–C–T method and H–B–T method

4 结论

(1) 温度场与应力场影响了碳质千枚岩破坏模式,在围压与温度均较低时呈脆性破坏,较高时逐渐转为延性破坏,存在残余强度,且峰后扩容现象显著。

(2) 根据峰值强度与围压关系,发现黏聚力、单轴抗压强度和参数n随温度升高呈线性增大,内摩擦角受温度影响不显著；基于Mohr–Coulomb 准则与Heok–Brown 准则,分别建立了热力耦合作用下碳质千枚岩破坏强度计算方法,即M–C–T 法和H–B–T 法。

(3) 通过计算,两种方法计算值均与试验值分布相似,这说明M–C–T 法和H–B–T 法都能较好地量化热力耦合作用下碳质千枚岩强度演化规律；误差分析表明,M–C–T 法计算误差介于−28.5%～7.7%,离散程度较大；H–B–T 法计算误差介于−8.9%～5.6%,离散性较小,且更偏向于安全。